载机横滚对机载预警雷达测高精度的影响分析
韩 伟 周升响 何成伟
(空军预警学院 武汉 430019)
0 引言
预警机在执行任务过程中,需要按照一定的规划线路航行,如“跑道形”和“双平行线形”,在某些时段需要进行机动,另外,载机也会受到大气环境中强气流的影响,产生偏航、横滚和俯仰等姿态变化,从而影响雷达的检测性能和探测精度[1]。国内外一些学者通过分析载机姿态对地杂波和目标回波的影响,给出了载机在各种姿态下的目标检测性能[2-8]。另外,一些学者从载机机翼遮挡电波的角度分析了横滚对检测性能的影响[9-10]。但目前针对机载预警雷达的探测精度的影响研究较少。
机载预警雷达在执行任务过程中进行的转弯机动,会使载机姿态会发生横滚,因此,横滚是其最为常见的一种姿态变化。本文研究载机发生横滚姿态变化对雷达测高精度的影响。以正侧面阵天线和三面阵天线为分析研究对象,采用单脉冲和-差测角方法来进行测高,首先建立了不同阵面雷达的载机横滚几何模型,在推导出单脉冲和-差法的测角精度的基础上,将载机横滚角并入测角方法中,从而推导出载机横滚条件下的测高精度,最后通过仿真得到不同横滚角下的测高精度变化情况,并给出了相应的结论。
1 载机横滚模型
图1为机载预警雷达下视探测示意图,参考坐标系为O-XYZ。图2为预警机机身坐标系XcYcZc,两个坐标系在载机无姿态变化时是重合的;如果载机发生横滚,且横滚角为Δβ时,两个坐标系的相对关系如图3所示。其中,目标在参考坐标系下的方位角和俯仰角分别为θ和φ。

图1 预警机下视探测示意图

图3 横滚角为Δβ时的坐标系
预警机机身坐标系和参考坐标系的相对关系可表示如下
(1)

(2)
预警机雷达天线有多种形式,如三面阵、正侧面阵、共形天线等,雷达天线位置与预警机机身有一定的角度差异,这里,仅考虑天线垂直放置且存在方位角偏差的情况,设天线坐标为XaYaZa,其坐标可表示为
(3)
(4)
其中,A为角度变化矩阵,θp为方位偏置角。
结合式(1)和式(3),天线坐标系和参考坐标系的相对关系为
(5)
式(5)中,θa和φa分别为目标在天线坐标系中的方位角和俯仰角。
当雷达天线为正侧面阵时,θp=0°;当雷达天线为三面阵时,在阵面与机身存在一定的角度偏差,如图4所示,三个阵面分别为前向阵、左斜侧阵和右斜侧阵,对应的方位偏置角θp分别为-90°,30°和-210°。

图4 预警机三面阵雷达天线
2 测高精度分析
2.1 单脉冲和-差法测角
单脉冲和-差测角法是通过比较雷达目标回波信号的幅度值来完成角度测量的[11],这里仅对俯仰角的测量进行分析。如图5所示,单脉冲和-差测角法使用两个部分重叠且指向不同的探测波束,形成两个独立的处理通道。当目标处于等信号轴,即波束交叠轴方向,两个通道接收到的信号幅度相等,此时,等信号轴所指方向即为目标方向。当目标偏离等信号轴向时,则其中一个通道信号幅度大于另一个。

图5 单脉冲幅度比较测角示意图
设天线方向性函数为F(φ),等信号轴的指向为φ0,两波束最大值方向与φ0的偏角为φk,目标回波信号方向与等信号轴的夹角为Δφ,则两波束的方向性函数可分别写成
(6)
两个通道接收到的回波信号分别为
(7)
式(7)中,K为回波信号幅度因子,与雷达发射功率、目标RCS等因素有关。
由u1和u2可求得其和值uΣ及差值uΔ分别为
(8)
当目标偏离等信号轴较小时,和值和差值分别可近似表示为
(9)
式(9)中,F′(φk)=dF(φk)/dφk是天线方向图在波束偏角φk处的斜率。
归一化的和差值可得
(10)
由式(10)中uΔ(φ)/u∑(φ)和Δφ的关系可知,角度Δφ可通过归一化的和差值得到,当测得目标的俯仰角后,可估算其高度值。
2.2 测高精度

图6 平坦地面
对于近距离目标,可以采用如图6所示的平坦地面模型近似给出目标高度的估计[12],即测高公式为
HT=Ha+RTsinφ
(11)
其中Ha为预警机高度,RT为目标距离(斜距),Ht为目标高度,φ为目标仰角。
由式(11)可知,目标高度估值与目标距离和目标仰角有关,对式(11)进行全微分,由于各个观测量(RT、φ)相互独立,可得到平坦地面模型下的高度测量均方误差为
(12)
其中各偏导数为
(13)
(14)
式(12)中,σRT和σφ分别表示目标距离测量和仰角测量的均方误差,假设载机横滚不影响σRT,则载机横滚对测高精度的影响主要取决于横滚对测角精度的影响。下面,主要针对单脉冲和―差波束法来分析载机横滚对其测角精度的影响。
由于和、差两个接收通道内都存在内部噪声,式(8)将变成
(15)

和、差两个通道的信号之比可以表示为
(16)
根据式(16),导出其数学期望和方差分别为

(17)
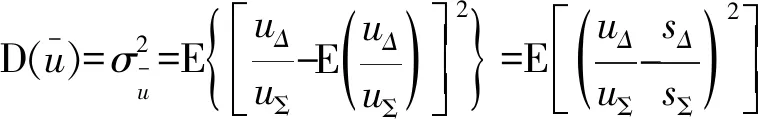
(18)

对式(17)微分,得
(19)

(20)
(21)
将式(18)代入式(21),得角度估计精度为
(22)
采用高斯函数拟合天线主瓣来具体分析,并且假设两个接收波束相同且相交于半功率点,得到对应的角度估计精度为
(23)
式(23)即为噪声带来的测角误差精度公式,其中kφ=2ln2,φ3dB为波束俯仰向上的3dB宽度。
2.3 横滚对测高精度的影响
载机横滚后,雷达波束在俯仰向会产生指向误差,使得目标与等信号轴的夹角发生改变,同时目标偏离和波束中心,使得SNRΣ减小,从而影响了测角精度。当载机发生横滚时,俯仰向上的测角精度可表示为
(24)
Δφ′=|φa-φ|
(25)

(26)
(27)
3 仿真实验
仿真中设SNRmax=20dB,主波束在天线坐标系中的方位角θ0=90°,Ha=8000m,Ht=9000m,σRT=200m,Rt=200km,目标初始位于等信号轴处,此时对应着最高的测角精度。
正侧面阵测高精度随横滚角的变化情况如图7所示。仿真结果表明:载机横滚使得测角误差的标准差增大,从而使得测高精度下降。这主要是由于载机横滚使目标偏离等信号轴,Δφ增大;同时,目标偏离和波束中心,造成SNRΣ的下降。

图7 正侧面阵测高精度随横滚角的变化情况
对于三面阵中的斜侧面阵和前向阵而言,载机横滚也会使波束的俯仰指向和目标回波功率发生变化,同样会带来测高精度的变化。
斜侧面阵测角精高随横滚角的变化情况如图8所示,前向阵测高精度随横滚角的变化情况如图9所示。仿真结果表明:不管是在斜侧面阵还是前向阵条件下,载机横滚均使高度测量值的均方误差下降,这也是由于横滚使得Δφ′上升,SNRΣ下降的缘故。其中,前向阵条件下,载机横滚对测角精度的影响很小,而斜侧面阵条件下影响较为明显,这是由于在前向阵条件下,横滚对Δφ′和SNRΣ的影响很小。而三种阵面雷达的测高精度受横滚的影响由大到小依次为正侧面阵、斜侧面阵和正侧面阵。

图8 斜侧面阵测高精度随横滚角的变化情况

图9 前向阵测高精度随横滚角的变化情况
4 结束语
本文以刚体模型条件下的正侧面和三面阵机载预警雷达为平台,研究了载机载机姿态变化对测高精度的影响,首先建立了两种天线形式雷达的载机姿态变化模型,然后从理论上分析了横滚对测高精度的影响。载机的横滚使得目标偏离等信号轴方向,和通道信噪比SNRΣ下降,从而影响了测角和测高精度的精度。仿真结果表明,载机横滚使得正侧面和三面阵雷达的测高精度均下降,且正侧面阵下降得最为明显,其次为斜侧面阵,而前向阵测高精度受到的影响最小。

