面向雷达数字化仿真的目标回波模拟方法研究
夏 云 卢 冀
(西安电子工程研究所 西安 710100)
0 引言
雷达数字化设计与仿真[1]作为雷达装备科研的数字孪生技术,采用数学建模构建雷达、目标、杂波、电子干扰等电磁环境模型,再仿真在设定的工作流程和环境下雷达、目标、杂波、电子干扰和电磁环境的相互作用,对雷达的设计乃至功能、性能进行测试与优化、验证与评估,有效提高产品全生命周期和功能的适用性,缩短研制周期,已成为当前雷达技术发展与竞争的焦点。
显然,目标回波仿真是雷达数字化设计与仿真技术需要解决的关键技术之一,已有目标回波模拟的研究主要包括目标RCS计算[2-5]和目标回波生成[6-8]两部分,目前针对目标RCS计算,大都采用专用电磁学计算软件生成单个目标或目标自身及其与场景耦合的回波幅度和相位变化量,目标回波生成就是根据目标RCS生成雷达回波波形。该技术领域就雷达数字化设计与仿真而言,面临的新的技术问题包括:
1)如何在数字化应用中对雷达波形进行参数化描述,这些参数可以通过仿真真实且高效地反映雷达与目标、杂波、电子干扰等相互作用的结果;
2)根据上述雷达波形参数,研究发射波形同目标相互作用的机理和波形参数变化结果;
3)根据回波参数和雷达发射波形,生成雷达回波信号。
本文将围绕上述问题,系统性地探索雷达数字化设计与仿真中的目标回波模拟技术和具体的实现方法,为数字化雷达目标回波模拟的实现与技术发展起到抛砖引玉的作用。
1 总体思路
在雷达数字化设计与仿真系统中,信息需通过离散的参数进行传输与处理,为了保证计算机仿真的可行性和高效性,选择的参数只限于描述信号与目标相互作用的结果,而不是描述发射信号的波形或时域采样值,如此可再根据发射信号波形及上述的参数生成雷达回波波形,其总体框图见图1所示。波形参数主要用于度量发射波形经目标的变化量,目标主要考虑位置、运动等空间属性及RCS等电磁属性,因目标运动及RCS变化的数据速率远小于发射波形变化的数据速率,考虑相互作用参数的变化能有效地提高了仿真效率,值得一提的是,波形参数还须能用于雷达同杂波、电子对抗等模型相互作用后波形变化的度量。
雷达数字化设计与仿真系统中,雷达回波信号是雷达发射信号与不同模型相互作用的组合,一般采用线性组合进行描述,假设与雷达进行作用的数字化模型有n(n=1,2, …,i,…,N)个,第i个模型的回波系数为Ci,回波函数表示式为Fi,则雷达回波Y可以描述为:
(1)
为了便于分析,只考虑单散射点目标n=1的情况,n≥2时根据式(1)和本文方法进行扩展。
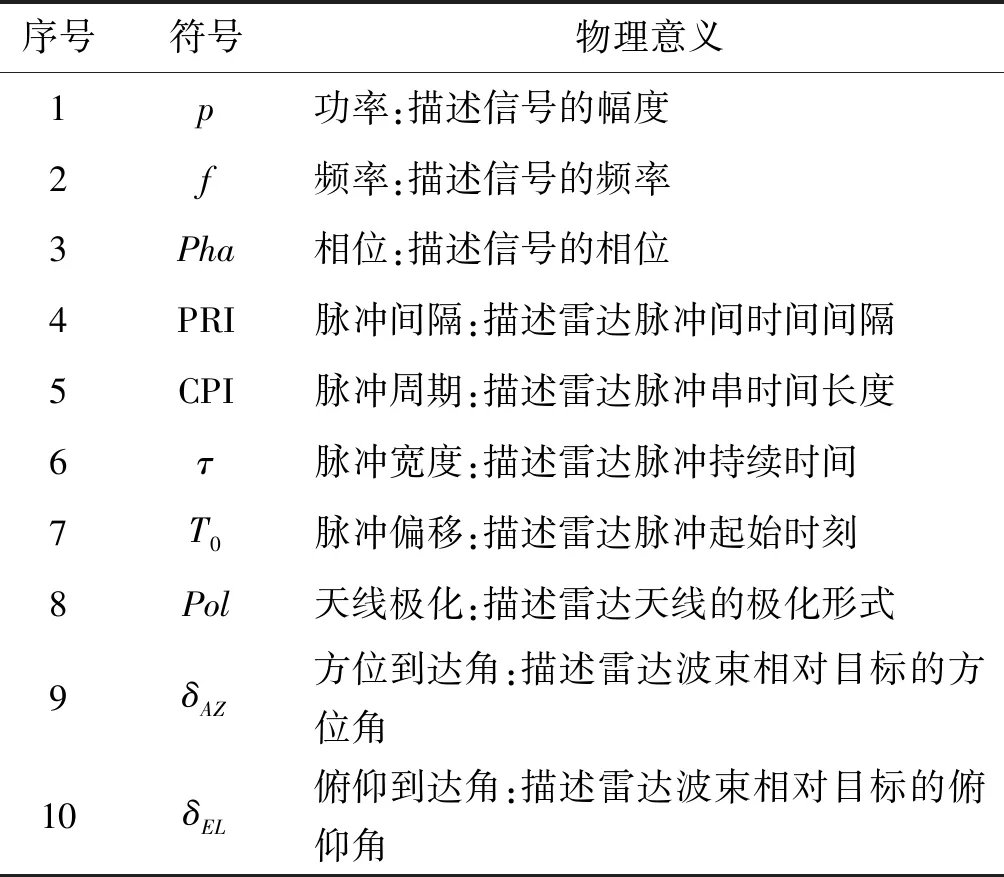
目前,雷达信号及信号处理方式都是基于三角函数的形式,那么,雷达的发射波形的复信号可以表示为
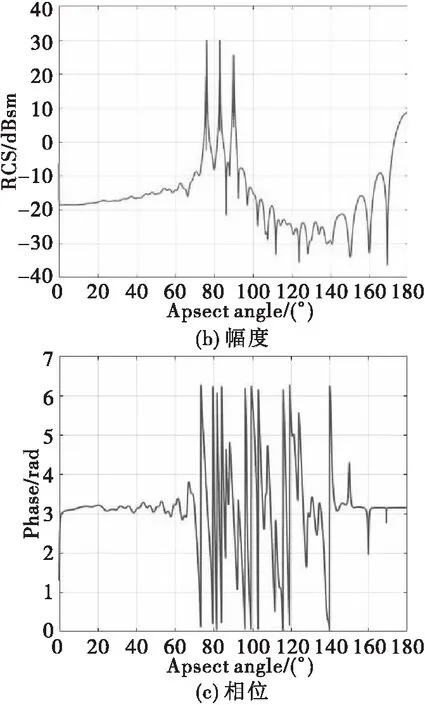
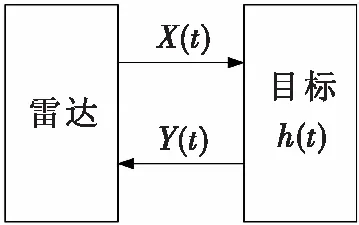
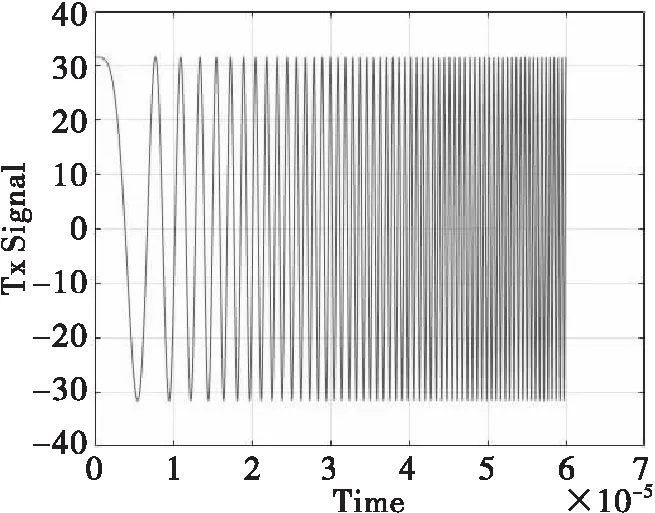
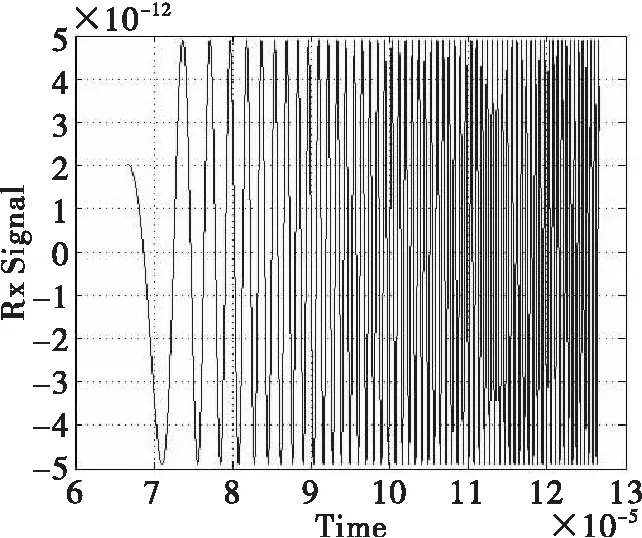
Si(t)=U(t)ej2πft,-∞ (2) 其中U(t)表示雷达发射波形的复包络,f表示雷达工作频率。雷达波形的类型可由U(t)表示,U(t)的复信号表示形式为 U(t)=g(t)f(t)ejφ(t),-∞ (3) 其中g(t)表示一定宽度的门函数,用于表示脉冲或连续波波形,f(t)ejφ(t)表示调制信号,其主要形式见表1所示。 表1 调制信号类型描述 类型2f(t)ejφ(t)Si(t)信号调幅连续调制:cos2πfct()脉冲调制:A(k1)ejφ0g(t)cos2πfct·cos2πft+φ0()A(k)·g(t)·cos2πft+φ0()调频连续调制:ej2πkfF(t)t脉冲调制:ej2πF(k1)tejφ0g(t)cos(2πft+2πkfF(t)t+φ0)g(t)cos(2πft+2πF(k)t+φ0)调相常数连续调制:ejkpP(t)g(t)cos2πf0t+kpP(t)()脉冲调制:ejP(k1)g(t)cos2πf0t+P(k)() 注1:I(k)(I=A,F,P)中的k可表示数值I(k)的持续时间。 2:调制信号还可以是调幅、调频以及调相信号的组合。 如表1所示,主流的雷达发射波形主要是门函数和三角函数的组合,对于连续波,脉内或脉组调制以及幅、频、相混合调制波形而言,可以理解为脉冲宽度、k以及I取值和组合关系的不同,本质上还是表1所示Si(t)描述的门函数与三角函数的组合,其包络取决于U(t)。 雷达回波So(t)相比发射波形Si(t)主要包括时延、幅度、频率和相位四个方面的变化,就目标回波而言,目标的空间属性会使回波发生时延、幅度、频率和相位变化,目标的电磁属性主要产生回波的幅度和相位变化。根据Si(t)和其相对目标的时延、幅度、频率和相位变化就可获取回波Si(t)。 雷达波形参数的设计需要满足两个要求:一是能表示雷达或典型雷达的波形,即能从这些参数中生成雷达发射或接收时序信号;二是能完全且方便地描述雷达发射波形与目标,以及杂波、电子战等数字模型相互作用后信号的变化。因此,雷达波形参数包括对自身波形时空频域参数的描述和相对目标等数字模型产生变化的时空频域参数。 雷达波形参数的描述见表2所列。 表2 雷达波形参数 序号符号物理意义1p功率:描述信号的幅度2f频率:描述信号的频率3Pha相位:描述信号的相位4PRI脉冲间隔:描述雷达脉冲间时间间隔5CPI脉冲周期:描述雷达脉冲串时间长度6τ脉冲宽度:描述雷达脉冲持续时间7T0脉冲偏移:描述雷达脉冲起始时刻8Pol天线极化:描述雷达天线的极化形式9δAZ方位到达角:描述雷达波束相对目标的方位角10δEL俯仰到达角:描述雷达波束相对目标的俯仰角 表2包含了雷达自身波形参数和相对目标模型时空频域波形变化的参数,其中p,f和pha用于描述雷达产生的三角函数波形,PRI,CPI,τ和T0用于描述雷达发射脉冲波形,pol,δAZ和δEL用于描述雷达天线极化属性和相对目标的角度,依此获取目标RCS属性(天线增益对雷达波形的影响将在雷达数字化模型设计中考虑,本文未涉及)。 表2列出了雷达目标回波模拟所需的波形参数,用于描述雷达波形及其与目标数字化模型相互作用的结果,后续针对满足雷达与杂波、电子战等数字化模型相互作用仿真的参数,将根据杂波、电子战等数字模型在本杂志后续论文中深入讨论。 雷达目标回波与目标的空间属性及电磁属性(RCS)相关,第一种方法是分别计算时空属性和电磁属性对回波的时延、幅度、频率和相位变化,另一种方法将时空属性和RCS综合考虑,由专业的计算软件通过电磁计算方法获取目标的耦合RCS,当然,耦合RCS还可将杂波、电子干扰的情况一并考虑,直接反映雷达回波的时延、幅度、频率和相位变化。数字化仿真是建立在多个数字化模型基础上的仿真系统,见式(1),因此,本文讨论第一种方法,显然文中方法也适用于第二种方法。 仿真系统可获知雷达和目标的空间三维坐标(Sx,Sy,Sz)和(Tx,Ty,Tz),雷达与目标间的距离R为 (4) 双程时延差Δt为 (5) 其中c表示光速。双程频率变化Δf为 (6) 双程幅度衰减Δd为 (7) 双程相位变化Δp为 (8) 目标RCS跟雷达工作频率和目标方位角AΘ及俯仰角AΦ相关,AΘ和AΦ为目标姿态相对雷达波束的坐标系下的投影角度,目标姿态定义如图2所示。 图2 目标姿态图 以目标正前、右侧及正上方向构建目标坐标系,目标围绕x、y和z轴的转角分别是俯仰角θ,横滚角φ和航向角ψ,那么目标俯仰角AΦ为 (9) 目标方位角AΘ为 (10) 其中α·β为向量α点乘向量β,即 α·β=|α||β|cos(α·β) (11) Vi(i=θ,φ,ψ)表示目标与对应坐标轴夹角i的单位向量,Vi是惯性坐标系向量经θ,φ,ψ姿态变换后生成的目标坐标系下的新向量,以图2为例,Vθ表示惯性坐标系向量先进行ψ角航向变换,再进行φ角横滚变换后得到的新向量,Vφ表示先进性ψ角航向变换,在进行θ角俯仰变换后的新向量,Vψ先进行θ角俯仰变换,再进行φ角横滚变换后得到的新向量。向量α绕β旋转ω,得到的新向量γ,γ的计算公式是 γ=(α×β)sinω+(1-cosω)(α·β)β+αcosω (12) VR表示目标(Tx,Ty,Tz)相对雷达(Sx,Sy,Sz)的位置单位向量,VR=[vTx,vTy,vTz]T,则VR为 VR=[vTxvTyvTz]T (13) 其中δAZ和δEL是目标相对雷达的方位和俯仰角,计算公式为 (14) (15) Vxy表示VR在目标XY平面上的投影,则单位向量 (16) 为了获取目标RCS,数字化仿真系统通过实时的雷达与目标位置,由式(13)-式(15)获得VR,再根据目标的姿态角θ,φ,ψ通过式(12)计算得到Vi(i=θ,φ,ψ),进而由式(16)获取Vxy,从而可根据式(10)和式(9)得到目标方位角AΘ和目标俯仰角AΦ。 目标RCS一般由频率f,天线极化Pol,AΘ和AΦ确定,可由几何光学(GO),物理光学(PO)及其它电磁计算等方法获取,图3显示了采用PO方法粗略计算的翼式布局导弹的RCS值,f=3.25GHz,水平极化,AΘ为0~180°,AΦ=0,其中图3(a)是导弹外形,图3(b)是幅度变化,图3(c)是相位变化。 图3 目标RCS 目标RCS度量了幅度和相位变化,即△dT和△pT,△dT和△pT会随着目标或雷达微动产生起伏和闪烁造成幅度和相位的变化,通常采用概率分布来计算这种变化。例如常见的分别采用瑞利和随机分布模拟幅度变化的Swerling Ⅰ模型和模拟目标散射点变化的角闪烁模型,此时△dT′和△pT′为 ΔdT′=(randn(1)+randn(1))·dT (17) (18) 其中randn(1)和rand(1)分别为均值为0、方差为1的高斯变量和范围在[0,1]的随机变量,idim,i=x,y,z分别表示目标宽度,长度和高度。 由表1可知,典型的雷达型号发射波形S(t)可以描述为 S(t)=g(t)ej2π(f+fc)tej2πf(t)tejP(t)ejφ0 (19) 目标的空间属性造成的时延、频率、幅度和相位变化分别为Δt、Δf、Δd和Δp,显然,此时发射波形的变化S′(t)为公式(20)所示。 S′(t)=Δdg(t-Δt)ej2π(f+fc)(t-Δt)ej2πf[(t-Δt)](t-Δt) ejP[(t-Δt)]ejφ0ej2πΔf(t-Δt)ejΔp (20) 再考虑目标的电磁属性,雷达和目标构成了一个简单的LTI系统,见图4所示,雷达发射信号为X(t),与目标相互作用后的回波信号为Y(t),目标作为接收与处理雷达发射信号的系统,其冲激响应为h(t)。 图4 雷达与目标构成LTI系统 显然,雷达的回波可以描述为 Y(t)=X(t)*h(t) (21) 那么 Y(jw)=X(jw)·H(jw) (22) Y(jw) ,X(jw)和H(jw)分别是Y(t) ,X(t)和h(t)的傅里叶变换,其中H(jw)又可以描述为 H(jw)=|H(jw)|ejφ(w) (23) 其中|H(ejw)|和ejφ(w)分别表示系统的幅度响应和相位响应。由上小节分析可知,式(23)为 H(jw)=ΔdTejΔpT (24) 雷达回波信号So(t)为 So(t)↔So(jw)=S′(jw)H(jw) (25) 由傅里叶变换的性质和三角公式,可推导式(25)为 So(t)=S′(t)ΔdejΔpT (26) 特别的,当雷达发射信号为一线性调频脉冲信号(不妨令μ=2)时,S(t)和So(t)可为 S(t)=g(t)ej2πftej2πt2ejφ0 (27) So(t)=ΔdΔdTg(t-Δt)ej2π(f+fc)(t-Δt)ej2πftej2π(t-Δt)2ejφ0ejΔpejΔpT (28) 综上所述,根据雷达信号功率p,工作频率f,相位Pha以及目标空间和电磁属性获取幅度、频率、相位和时延变化,其中目标空间坐标根据仿真进程实时计算,目标RCS根据天线极性Pol、方位角δAZ、俯仰角δEL及目标姿态获得,最后根据PRI、CPI、τ、T0等(脉内、脉组等调制波形需更多参数)典型雷达波形参数和式(4)-式(25)计算目标回波。 假设雷达波形参数为:P=1000W,f=3.25GHz,Pha=0,τ=60μs,带宽B=2MHz,LFM信号,只考虑单个脉冲信号,未进行积累处理,仿真中PRI和CPI未考虑。 目标为图3所示导弹,距离雷达10km,径向速度300m/s,相对雷达角度AΘ=90°,AΦ=0,仿真获取了单个脉冲内的雷达回波,假设T0=0,为了便于波形显示,忽略了cos2πft部分。 图5和图6分别给出了雷达发射波形和雷达目标回波,论文只通过单一的静态参数以验证了本文方法的可行性和可用性,然而在真实场景中,雷达波形、雷达与目标的δAZ和δEL,目标空间等参数随间变化而变化,需要根据实时的参数,参考本文方法进行动态计算,可生成动态场景的雷达目标回波。 图5 雷达发射信号波形 图6 雷达目标回波信号 在雷达数字化仿真系统中,为了保证雷达与目标、杂波、电子干扰等模型数学建模方法和接口的一致性和通用性,论文从雷达目标回波这一基础问题入手,主要从波形参数、模型互动、回波生成等三个方面,较为系统地阐述了数字化系统中雷达目标回波生成的理论原理和计算方法,为雷达数字化设计与仿真系统模拟雷达目标回波提供了理论参考和方法依据,并可借鉴于为雷达杂波及电子对抗的仿真模拟研究与实现。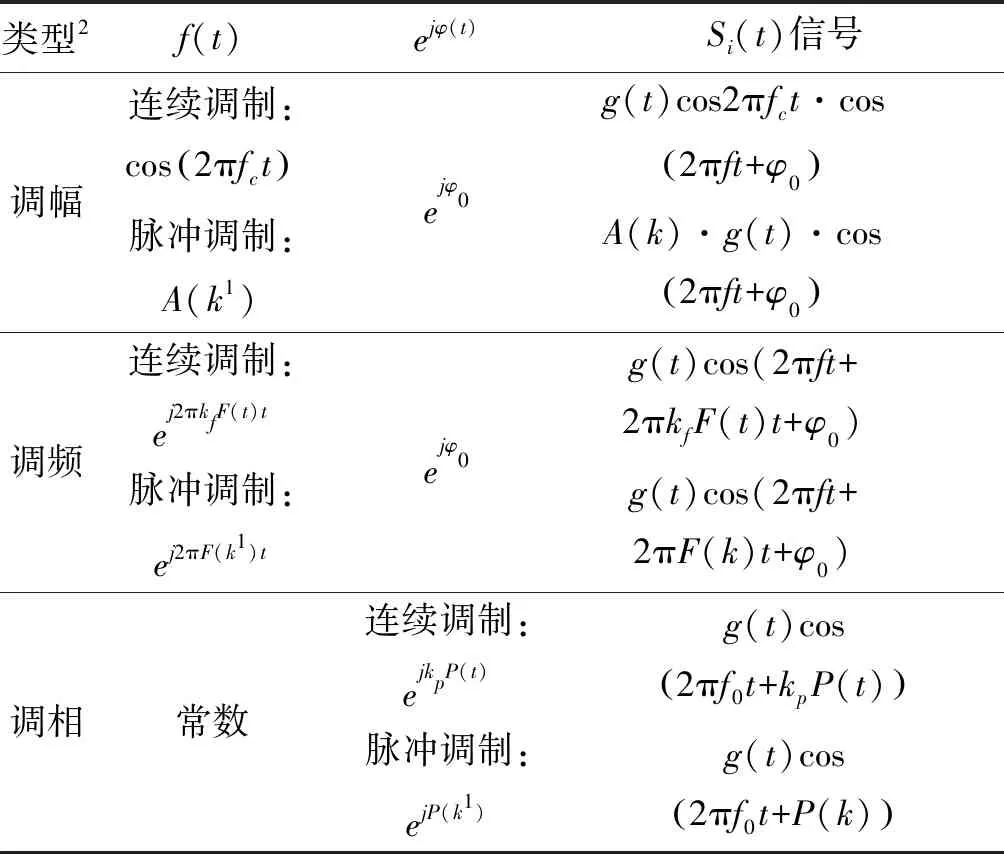
2 设计原理与方法
2.1 雷达波形描述参数
2.2 波形参数与目标相互作用

=[sinδAZcosδELcosδAZcosδEL-sinδEL]T
2.3 目标回波生成
3 仿真结果
4 结束语

