基于压缩感知的探地雷达成像算法研究
张永宁 薛永刚 陈 皓 李 江 付晓庆
(西安应用光学研究所 西安 710065)
0 引言
探地雷达是一种有效的浅层隐藏目标(岩石、泥土、砾石等材料)探测技术。利用电磁波在地下介质中传播时遇到存在电性差异的分界面时发生反射,根据接收到的电磁波振幅强度、波形和时间的变化等特征参数推断地下介质的空间位置、形态、埋藏深度和结构等信息。通常合成孔径成像要求采集大量的时空数据,通过探地雷达扫描感兴趣的区域并且记下空间域反射回来的时间信号。常用的探地雷达成像算法如时域标准反投影算法[2]和距离偏移算法[3],都是利用标量波动方程建立目标函数关系式,从而对目标散射数据进行成像。通常地下潜在目标仅占雷达探测区域很小部分,以上算法为了得到更好的成像效果,按照奈奎斯特采样率对地下目标反射信号进行采样,在没有考虑目标区域所占探测区域很小一部分的先验知识,其要求探地雷达对目标回波信号进行采样时,在满足奈奎斯特采样定理的条件下,尽量设置高的采样率,以获取足够多的原始成像数据,这些算法导致探地雷达采样数据量大、硬件设计复杂、测量时间较长。
压缩感知理论是建立在逼近原理和稀疏信号表示方法基础上的新研究领域,它充分地利用了雷达目标回波信号结构所具有的稀疏特性,利用欠奈奎斯特率采样数据的非相关测量实现高维稀疏信号的感知。压缩感知算法摒弃了原始信号采样中的冗余信号,并通过连续的时间信号变换处理,得到原始信号的压缩样本,最后在雷达数字信号处理中采用优化处理算法来处理压缩后的原始信号样本。目前压缩感知理论在通信、图像处理、光学、微波成像等众多领域引起高度关注。本文利用探地雷达探测目标区域具有稀疏性的先验知识,以压缩感知为理论基础,通过对合成孔径雷达回波信号的稀疏性进行分析,提出了合成孔径探地雷压缩感知成像算法。该算法不但能提高探地雷达的成像性能,同时还可以缩短数据采集时间、降低探地雷达采集系统硬件成本,实现了以较少资源实现探地雷达的高分辨率探测成像。
1 压缩感知的基本内容
当信号在某个变换域上可稀疏表示或者可进行压缩时,可用与变换矩阵非相干的测量矩阵将变换系数线性投影为低维观测向量[4],这种系数线性投影法具有重建信号所必需的所有重要信息,通过进一步求解稀疏最优化问题,可以从低维观测向量精确地重建原始高维信号。
将给定的信号在己知函数集上进行分解形成信号稀疏变换,通过在变换域上表达原始信号,用少量的基函数来准确地重构出原始信号。
RN中的离散信号x[n],n=1,2,…,N表示为
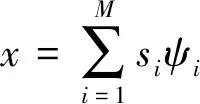
(1)

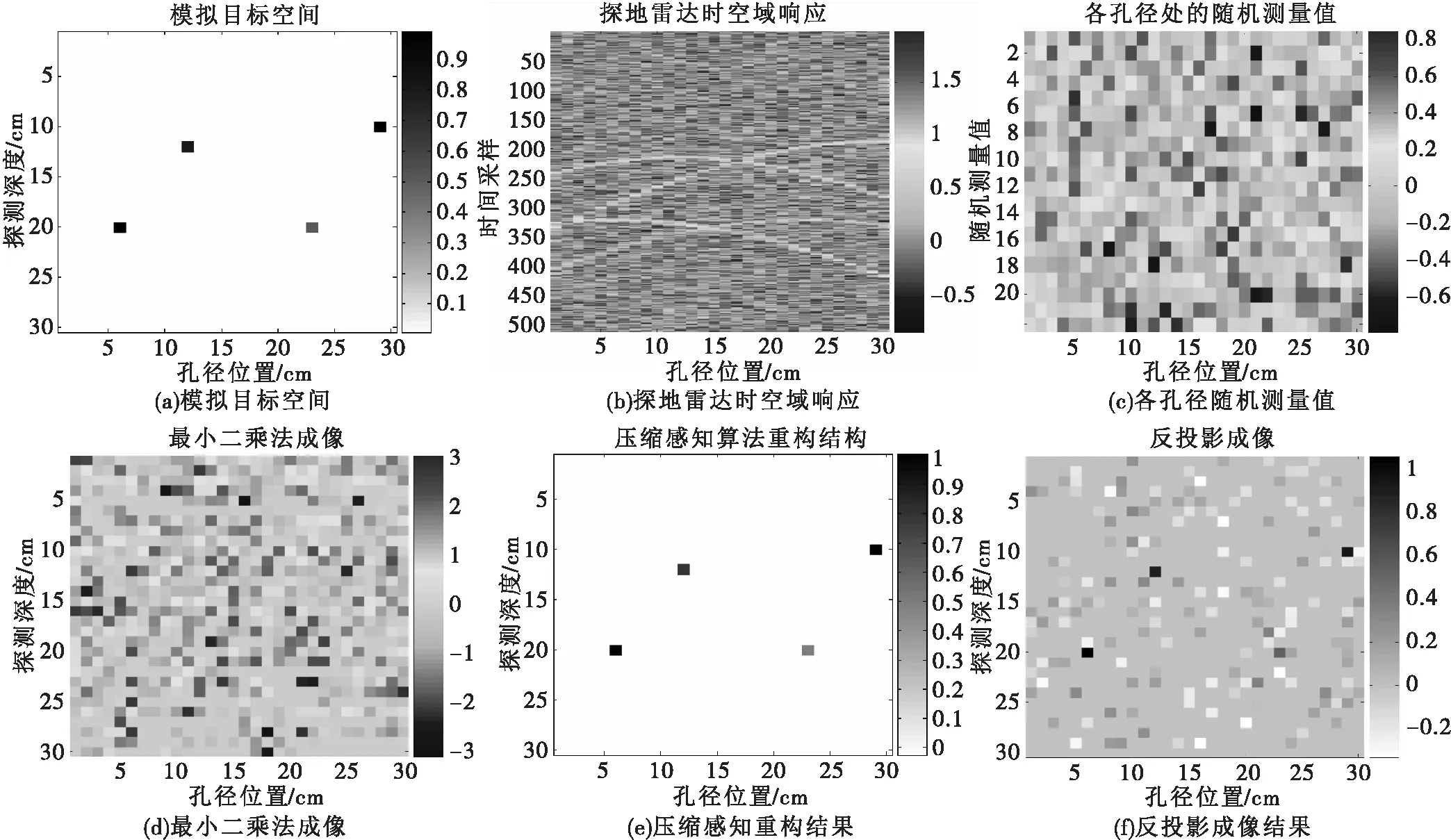
压缩感知理论直接对稀疏信号进行采样,x为任意N维K阶的稀疏信号,s通过x在空间RN的M=c(μ2(Φ,ψ)logN)K(M< y=Φx=ΦΨs (2) 式(2)中y表示M维随机测量值,Φ为M×N维随机测量矩阵,常量C一般很小,μ(Φ,ψ)是Φ与ψ之间的相关值。当Φψ满足有限等距特性[5]时,通过求解l1范数约束最优化问题 (3) 可从欠定方程式(2)的M个测量数据中用稀疏表示s还原原始信号x。 探地雷达使用雷达电磁脉冲对地下成像,当发射电磁波从不同的电介质边界做出反射时,接收天线记录反射回来的信号。本文使用常规的点目标模型,利用该模型得出延迟时间的反射回的接收信号 (4) s(t)是发射信号,τi(p)是天线在第i个孔径点时收发天线和目标p之间总的往返时间延迟,σp是目标的反射系数,Ai,p是衰减和传播损失的缩放比例因子。 通过探地雷达在空间中移动来收集从不同的扫描区域反射回的时间数据,这些扫描点的集合,构成了合成孔径雷达的接收时空数据。系统使用收发天线分开固定装置,收发天线间距为dtr,如图1(a)所示。计算传输时间τi必须知道从发射天线到目标,再到接收天线波的传输路径,以及不同介质中的波速。 图1 探地雷达数据组图 两种不同的媒介如空气和土壤有不同的电介质特性,根据斯涅尔折射定律改变波的传播方向,波的折射对于拟域成像特别关键,因此精确计算折射点的方法至关重要[6]。确定折射点后,图1(a)中的d1:4,i四个部分的距离路径可计算得到,时间τi的计算为 (5) 随着收发天线的移动收集扫描区域的数据,一个单目标在x=0,深度在10cm位置处时,探地雷达天线沿单道方向从-70cm到70cm进行扫描,得到一个单点目标时空域空间变换曲线响应图如图(b),当采集这个感兴趣的区域的数据时,这个过程叫合成孔径成像。 忽略目标之间的相互影响,探地雷达在扫描点(ux,uy)的时空数据的测量值计算为 (6) τ(ux,uy,x,y,z)是从发射天线到目标空间点(x,y,z)再到接收天线的总的传输时间,σ(x,y,z)是在目标空间点(x,y,z)的反射系数,AL(ux,uy,x,y,z)代表传播损失。使用测量值d(ux,uy,t)的目的是为了产生反射剖面,即目标空间的成像。 标准成像算法对每一个时空域如图1(b)数据采集系统的脉冲响应数据进行匹配滤波,时域标准反投影算法[6]表达式为 f(x,y,z)=∭w(ux,uy)d(ux,uy,t)× (7) w(ux,uy)是在扫描区域的加权函数,通常用于减小图像的旁瓣,δ()是脉冲响应。 在探地雷达工程应用中,当雷达对地下目标进行探测时,目标探测区域通常可认为是由多个离散的散射中心组成,目标散射中心只占据雷达探测区域的很小一部分空间单元。把雷达探测成像区域均匀的离散分成N个点散射目标,通过离散的空域目标空间πT创建每一个离散空域探地雷达模型。该模型产生一个有限系列的点目标β={π1,π2,…,πN} ,每一个πj是三维向量[xj,yj,zj],对于i孔径点,ψi的j列是相对于目标在πj的接收信号,第j列的n个元素可以表示成公式(8)所示。 (8) 其中:tn=t0+n/Fs0≤n≤Nt-1,分母是时间信号能量,Fs是采样频率,t0是初始时间,Nt是暂存采样数目,对β中每一个可能的目标点重复计算式(8),在i孔径点产生字典ψi的大小为Nt×N,接收信号表示为 ζi=ψib (9) 其中向量b表示加权系数,其满足稀疏性,表示为探测目标像矩阵中的各个元素。如果探测目标处在πj网格处时,向量b的第j个元素即为πj对应的反射系数,否则其元素值为0。 标准探地雷达接收器通常需要很高的采样率,当目标空间是稀疏时,该文提出的基于压缩感知的数据采集模型用一定量的雷达测量信号来重构雷达稀疏信号。一般情况下,信号x的测量值写成y=Mx,M是测量矩阵。在第i个孔径处 βi=φiζi=φiψib (10) βi是测量向量,Фi是M×Nt的测量矩阵(M≪Nt)。压缩感知理论要求矩阵ΦΨ满足约束等距特性,保证Фi的行不能由ψi的列稀疏表示,反之亦然。随机测量矩阵Фi服从独立同分布或者伯努利分布。 (11) (12) 其中:ui=φini~N(0,σ2),ni为系统噪声向量。b的重建问题可通过以下方法得到 (13) 或者 min‖b‖1s.t. ‖β-Ab‖2〈ε2 (14) 其中A=Фψ,ε1,2是正规化参数。通过求解式(13)、式(14)代表的约束问题,可以较高概率地从含有噪声随机测量信号中重构出加权系数向量b。 选面积为900cm2的地下二维模拟区域进行探测试验,用π来标记目标空间。将地下二维目标空间划分成30×30=900个等面积的网格,记作∏=[∏1,…,∏j,…,∏900]T,目标空间π的加权系数向量则用b=[b1,…,bj,…,b900]T表示。在地下模拟目标空间内随机的放置4个模拟点目标,目标分布情况如图2(a)所示。 反投影成像算法成像结果如图2(f)所示,该算法首先计算出孔径i处的探测信号从发射天线经目标空间第πj个目标反射进入接收机后的延时量τi(πj),并将所有孔径中具有相同延时量的回波信号进行相加,利用全部目标空间512×900个目标回波数据恢复出目标函数b。 图2 仿真探测试验组图 通过数据仿真和实验结果表明,基于压缩感知的探地雷达成像算法与传统探地雷达成像算法相比,具有分辨率高,采集数据少,硬件实现简单以及更易于目标辨识等优点。在实际探地雷达实时成像应用中,需要进一步研究效率更高的凸优化问题计算方法,并且选择使用一个更广义的测量矩阵,即一个完整的随机矩阵代替现有对角阵Ф,更好地实现基于压缩感知探地雷达实时成像的工程应用目的。2 压缩感知合成孔径探地雷达成像原理

δ(t-τ(ux,uy;x,y,z))dtduxduy2.1 创建探地雷达数据字典
2.2 压缩感知数据获取
2.3 压缩感知探地雷达成像
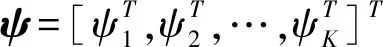
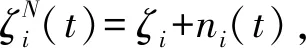
3 实验仿真及分析

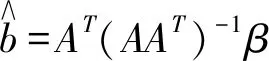
4 结束语

