高倍抽取率的数字下变频设计

张 凯 陈 龙 秦 奋 田 宇 陈 翔

(上海航天电子技术研究所 上海 201109)

0 引言

数字下变频是宇航测控通信领域的关键技术之一。宇航测控应答机在接收返向射频信号，经射频前端滤除绝大多数不需要的信号并下变至中频信号后，再经高速模数转换器(Analog to Digital Converter，ADC)进行采样量化，最后经FPGA实现相应的数字信号处理(测距、控制及数据传输等信号处理)。其中，在AD采样过程中，通常采用采样频率远高于基带信号带宽的频率进行过采样，其目的为减少使用额外抗混跌滤波器的成本[1]，那么，数字中频信号的数据率将过于庞大，因此，为减少不必要的计算量必须对数字中频信号进行高倍数抽取。

正交数字下变频主要包括数字混频器(即乘法器)、数字控制振荡器(Numerically controlled oscillator，NCO)、低通滤波器以及抽取器等部分组成，如图1所示。在功能上，数字控制震荡器与乘法器用于将数字中频信号进行正交变换和下变频，以达到数字中频信号变换至低通型信号的效果；低通滤波器用于抽取前抗混叠滤波；抽取器用于降低数字中频信号的采样率。为实现较高倍数地抽取，数字下变频中的抽取和滤波是关键。本方案主要基于某型号深空探测环境的特点，考虑中频信号载波频率高，而基带数据带宽很窄的特点(载波频率：70.1MHz；采样速率：40MHz；基带数据带宽26kHz)，需设计一数字下变频进行640倍抽取至零中频。

图1 正交数字下变频基本结构[2]

1 高倍抽取率的数字下变频方案设计

本方案应用于宇航类深空测控应答机，基于图1数字下变频的基本结构，图2为本文方案的整体框图，整体框图主要可以分为正交混频器和抽取滤波结构。

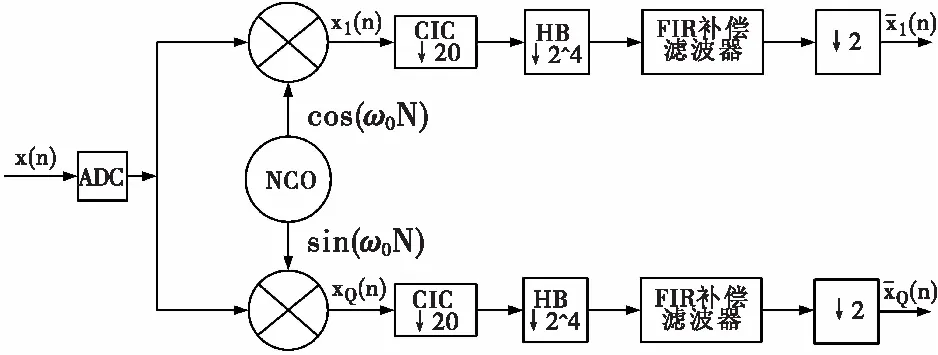
图2 高倍抽取率数字下变频方案框图

1.1 数字中频正交化设计

为了使数字中频信号变换至零中频信号，正交混频器需要对其进行下变频和正交化。正交混频器主要包括NCO和数字乘法器两部分。

测控应答机的软件无线电前端的A/D采样，采用香农带通采样定理，其中频信号载波频率f0为70.1MHz，采样频率fs为40MHz，基带数据带宽±26kHz。经带通采样定理分析可得，采样后距离零频最近的载波频率为±9.9MHz(2×fs-f0和-2×fs+f0)。图3所示为带通采样频域示意图。因此，正交混频器的NCO的本振频率选择为9.9MHz，数据速率应与中频AD采样速率一致，即40MHz。

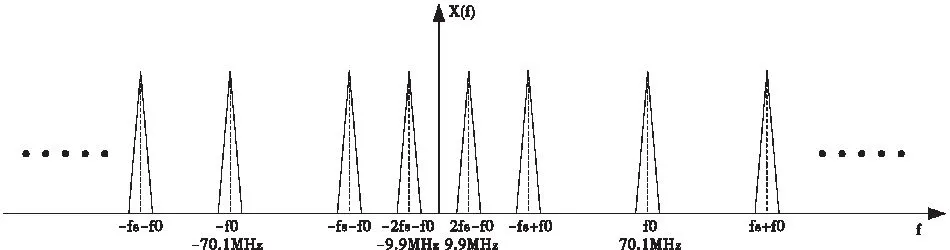
图3 带通采样频谱示意图

1.2 抽取滤波结构设计

在较高抽取倍数的DDC中，工程上大都采用多级抽取技术的方式进行实现，那是因为与单次抽取方式相比较，多次抽取方式的计算量会较小[1]。如图2所示，为实现采样速率的高倍率降速(640倍抽取)，抽取滤波结构同样采用多级抽取技术，即通过CIC滤波器，HB滤波器以及FIR滤波器级联抽取的方式进行实现。DDC中I路和Q路的抽取滤波结构和参数是相同的，如图4所示为其中一路抽取滤波结构的详细框图。

图4 抽取滤波结构的详细框图

1.2.1 CIC抽取滤波器

如图5所示，多级级联CIC抽取滤波器由积分器、抽取器和梳状器级联组成。它具有结构简单，无需乘法器，运算速度快，抽取因子D不必是2的幂次方等特点，因此其在高速抽取系统中有着广泛地应用，通常作为抽取滤波系统的第一级。

积分器是一单极点累加器，其传输函数为

(1)

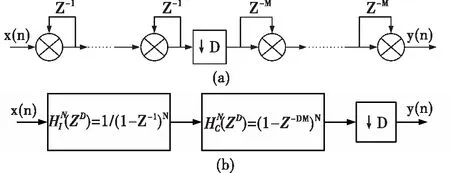
图5 多级级联CIC抽取滤波结构图

梳状滤波器本质上是一微分器，其传输函数为

HI(z)=1-z-M

(2)

其中，M为微分延迟因子，一般取值为1或2。

在CIC抽取滤波器中，积分器工作在高采样率fs中，而梳状滤波器工作在较低的采样率fs/R中。为了计算CIC滤波器的等价频率响应，将图5(a)的CIC抽取滤波器进行等价变换至图5(b)所示。因此，在高采样频率fs下的N级CIC抽取滤波器整体传输函数和幅频响应分别如公式(3)和公式(4)[3]

(3)

(4)

其中，D为抽取因子，N为CIC级联数。

本方案在权衡带内平坦和旁瓣抑制等因素，拟采用3级CIC滤波器。本方案的CIC抽取因子D为20远远大于1，微分延迟因子M定为1。MATLAB仿真的CIC频谱特性如图6所示。

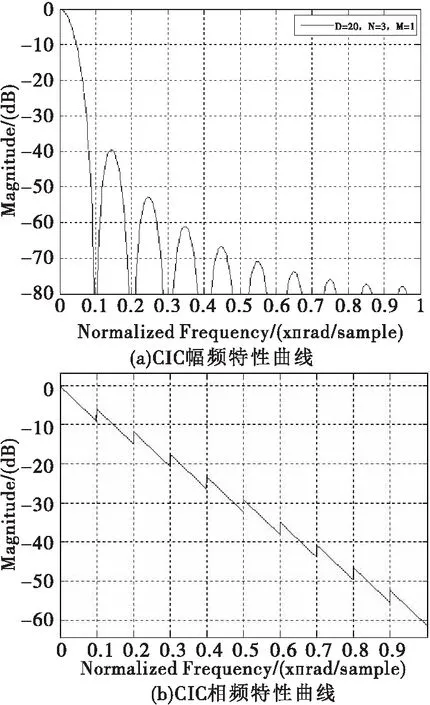
图6 CIC抽取滤波幅频与相频特性

1.2.2 HB滤波器

HB滤波器是一种特殊的FIR滤波器，与普通FIR滤波器相比，HB滤波器可以使2倍抽取的每秒乘法次数减少一半，因此很适合与2倍抽取器级联实现高倍抽取。HB滤波器具有以下特点[4]：

1)滤波器的通带和阻带对称，即阻带带宽与通带带宽相等(ωs=π-ωp)，且通带纹波和阻带纹波相等(δs=δp)，其中ωp和δp分别为通带截止数字角频率和通带纹波，ωs和δs分别为阻带截止数字角频率和阻带带纹波。

2)滤波器的系数具有偶对称性，且滤波器阶数为偶数。

3)半带滤波器的频率响应H(ejω)满足公式(5)-公式(7)和图7所示特点。

H(ejω)=1-H(ejω)

(5)

(6)

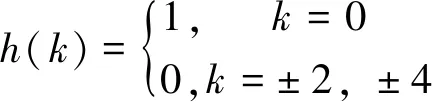
(7)

图7 半带滤波器频谱特性

高速率(40MHz)零中频信号在经过抽取滤波结构中的第一级CIC抽取滤波(CIC的抽取因子D=20)后，其采样速率降为2MHz，经过4级HB滤波器16倍抽取，其采样速率降为125kHz。为保证基带信号带宽内信号的平坦性，本方案在多级HB滤波器级联的最终通、阻带纹波指标定为0.001dB，由系统纹波指标可由公式(8)、公式(9)计算合适的各级HB滤波器的通、阻带纹波[4]。

(8)

k=lg(D)

(9)

其中，δi为各级HB滤波器的纹波值；k为级联数；D为HB抽取滤波系统总抽取倍数。

综上所述，各级HB滤波器的通、阻带纹波为0.0025dB(0.001dB/4)。除此之外，为保证整个抽取滤波系统的实时性，减少时延，应尽可能地减少HB滤波器的阶数。本方案借助MATLAB强大的滤波器仿真建模能力，对各级HB滤波器进行设计仿真。如图8为各级半带滤波器的频率和相位特性。

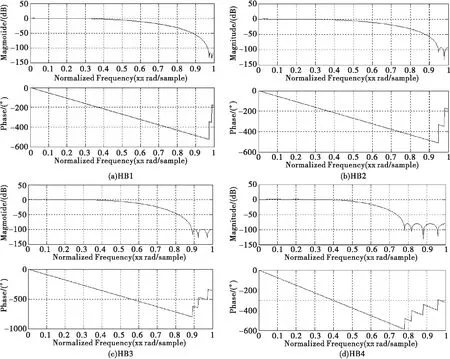
图8 各级HB滤波器的频率与相位特性

表1 各级HB滤波器的阶数

滤波器名称HB1HB2HB3HB4阶数661014

1.2.3 FIR补偿滤波器

从图6 CIC仿真图可知，当级数较大时旁瓣抑制得到增强的同时主瓣滚降特性也较明显，影响带内的平坦度，因此需要想办法在通带内对CIC进行补偿。

CIC补偿滤波器的基本思路为，在信号带宽内，级联一幅频响应为公式(4)的倒数的滤波器，而带外幅频响应为0。公式(10)给出了CIC补偿滤波器的通带内幅频响应。倘若抽取因子D很大时，那么可近似为sinc-1函数[5]。

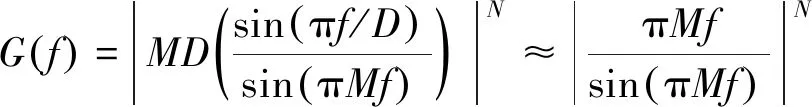
(10)

考虑到在高采样率条件下，对CIC进行补偿滤波，其FIR补偿滤波器的阶数较高，需要进行多次乘加运算，势必将占用大量的硬件资源，因此FIR滤波器应安排至抽取滤波系统的最后一级。本方案的每级抽取滤波器都是先进行抗混跌滤波然后抽取，那么如图4可以看出，CIC至FIR补偿滤波器进行了16倍抽取，因此需对公式(10)中的f除以16得到

(11)

FIR滤波器的通带内幅频响遵循公式(11)，借助MATLAB中的fir2函数对FIR滤波器进行设计。图9为CIC补偿滤波器与CIC滤波器级联的归一化频谱特性曲线，图中采样频率为62.5kHz。

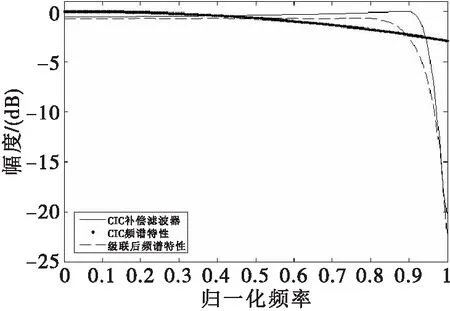
图9 FIR补偿滤波器的频谱特性

2 FPGA实现

上文中已经对本方案的设计方法进行了论述，下面将简述方案FPGA实现。如图2所示，方案包括正交混频器和抽取滤波结构两大部分。FPGA程序设计采用自上而下层次化的设计思路。顶层模块实现模块间级联，而底层模块完成各组成部分的逻辑运算功能。

正交混频器在FPGA实现上较为简单，NCO和乘法器可以采用创建与例化Xilinx ISE自带的IP核进行实现，简化设计流程与方法。FPGA实现的难点在于抽取滤波结构部分。对于各级抽取滤波器的底层模块设计思路如下：

1)根据CIC的组成结构，细化CIC模块为积分器、抽取器和梳状器三个子功能模块，并在CIC模块中进行子功能模块的级联。

2)各级HB滤波器与FIR补偿滤波器皆是先滤波后抽取，从第1节中的分析知道，HB滤波器实质上为FIR滤波器，因此这两种滤波器皆可采用创建与例化Xilinx ISE自带的FIR IP核进行实现。

3)MATLAB生成的滤波器系数大都是全精度的小数，必须对系数进行量化才可适用于FPGA逻辑运算。

4)在保证精度和防止数据溢出的条件下，数据流的运算字长的选取，采用高位截取的方法。

3 仿真分析与验证

本方案FPGA应用平台为Xilinx公司的XC4V SX55，用Xilinx公司的开发环境Xilinx ISE与Modelism进行时序仿真分析，以方便设计者较为直观地把握整体方案的可行性。

仿真步骤如下：

1)借助Matlab数学建模的方式产生激励源信号，例如以载波频率为70.1MHz，采样率为40MHz，信噪比为25dB，基带信号可用小于26kHz的正余弦信号作为激励源进行验证。

2)在ISE中编写程序实现本文阐述的方案功能。

3)调用Modelsim进行时序分析。

图10为本方案的DDC的时序仿真结果，图中信号时域框图从上至下分别为时钟、复位、数据中频信号、以及DDC输出的IQ两路时序波形，从图10可以明显观察出低频基带信号已清晰地剥离出来。

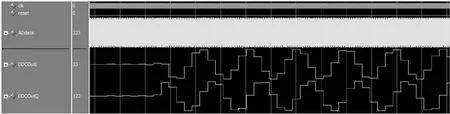
图10 时序仿真结果

4 结束语

本文论述了一种基于正交混频器、CIC滤波器、HB滤波器和CIC补偿滤波器级联实现的高倍抽取率的数字正交下变频设计方法。为实现文中640倍超高抽取率数字下变频方案，其难点在于抽取滤波结构的设计规划。本文为保证高效抽取，采取的措施是在高采样率下进行高效滤波器级联并将运算量大、效率低的FIR滤波器安排至最后一级抽取滤波；除此之外，设计CIC补偿滤波器进行平滑带内。文中设计方案方法通过仿真与FPGA硬件验证了其实现的可行性、有效性。