融合多特征表示和超像素优化的双目立体匹配
郭 倩,张福杨,孙农亮
山东科技大学 电子通信与物理学院,山东 青岛266590
1 引言
双目立体匹配一直是计算机视觉领域的一个基本问题和研究热点,其核心思想是在两幅图像之间建立对应关系,该技术可应用在3D 模型、机器人导航、三维场景重建、零件检测以及基于图像渲染等领域。20 世纪90年代以来,立体匹配研究出现了两个方向,一种是偏重于实时性的局部特征法,另一种是偏重于算法准确性的全局匹配算法[1]。局部立体匹配通常可分为四个步骤:代价计算、代价聚合、视差计算和视差精化[2]。全局立体匹配通过随机生成视差粗略图,最小化全局能量方程,得到最优视差图。采用的匹配技术主要有置信度传播算法[3]、图割算法[4]、动态规划算法[5]、二次规划算法[6]等。
全局立体匹配方法在应用中匹配精度高,但实际执行效率却很低,无法满足实时性的要求[7]。局部立体匹配算法以像素点为中心构建局部窗口,通过计算窗口内的像素相似性求取初始匹配代价,具有计算速度快、易于实现的优点。常用的像素相似性度量方法主要有:像素点灰度差(SAD)、归一化交叉变换(NCC)、Rank 变换、Census变换[8]等,并通过在一定范围内代价聚合得到初始视差值。但是由于支持窗口的大小难以选择,Zhang等人[9]将自适应支持窗口用于代价聚合过程,Mei等人[10]对文献[9]进行改进,增大自适应窗口的约束条件,提高匹配精度。Lee 和Hong[11]通过对左右图像分别求各自的自适应支持窗口进行AND 操作,得出最终的代价聚合支持窗口,对文献[10]进一步改进。文献[12-13]分别提出基于最小生成树(MST)和分割树(ST)的代价聚合方法,在匹配精度上取得了较好的效果。Kang等人[14]利用人眼视觉由粗到细的特征,将CTF 框架用于立体匹配,在视差精度上进一步得到了改进,速度上并没有很大的提升。马龙等人[15]利用强相似点检测对双目图像进行立体匹配,提高了匹配速度,但是在缺乏纹理区域匹配精度不高。文献[16]将超像素分割应用于立体匹配,并通过对超像素建立马尔科夫场进行匹配代价聚集,视差效果得到了较好的改进,但是在缺乏纹理区域却不能很好的匹配。
本文基于多特征信息进行代价计算,利用超像素分割将具有相似度高的像素聚合为超像素,并基于米字骨架自适应搜索方法计算聚合范围。在视差精化步骤,采用左右一致性检测检测出错误匹配点,并对错误匹配点进行8个方向极线扫描优化,利用超像素分割结果作为检测视差结果是否正确的判断条件,进一步修正了匹配中常见的毛刺现象。
2 改进算法描述
本文算法主要通过权重融合AD、Census、Edge信息代价计算;利用超像素分割SLIC算法生成超像素,并基于米字骨架对初始匹配代价进行代价聚合;利用Winner Take All 进行视差求取;最后利用本文提出的超像素优化算法进行优化,生成最终的视差图。具体的算法流程图如图1所示。

图1 本文算法流程图
2.1 结合多特征表示的代价计算
局部立体匹配算法中,AD(Absolute Difference)算法不需要复杂的乘除法运算,因此运算速度快,但对噪声和光照较敏感,算法精度随信噪比增加和光照不均而下降[17]。Census算法对光照变化的适应性好,对由光照不均引起灰度变化有很好的修正作用[18]。在立体视觉匹配过程中,边缘信息的处理比较复杂。由于边缘位置视差具有很大的不连续性,在一幅图像中体现场景特征最明显的位置往往在图像的边缘位置上[19],这同时也为研究提供了一个非常有意义的线索。因此,在AD、Census算法的基础上,加入Edge图像的边缘信息,能够增强立体匹配对边缘的辨识度,减少在边缘匹配错误的像素数量。
AD(绝对差)算法通过计算在同一位置左右目图像的信息差异来得到匹配代价,像素(x,y)在视差为d 时的计算公式如下:
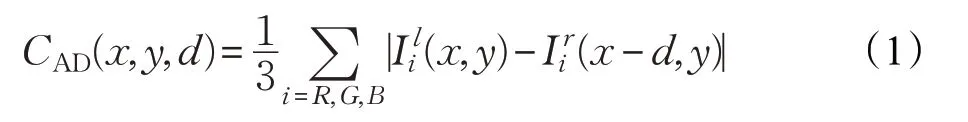
Census变换是一种局部非参数变换[20],通过比较两个像素的Census 编码得到汉明距离作为匹配代价。Census 编码以窗口中心像素(u,v)为基准,如果窗口中的一个像素(m,n)的灰度值比中心像素大,则将该位置的编码置为0,否则置为1。Census 变换示意图如图2所示。

图2 Census初始代价计算
经过以上Census 变换得到的初始计算代价如下所示:

式中,Cl(x,y),Cr(x-d,y)分别为匹配图与参考图中以(x,y),(x-d,y)为中心的匹配窗经过Census 变换之后的比特串,d 为视差值。
Canny 算子利用一阶差分偏导计算图像的边缘特征,将图像边缘像素值置为255,非边缘像素值为0,得到边缘初始代价CEdge。由于边缘特征具有特殊的作用,往往代表着深度不连续区域。因此在代价融合时,先将CCensus、CAD代价融合,然后将边缘位置的代价替换为CEdge,增强了立体匹配在边缘区域的辨识度。计算公式如下:

其中,λCensus、λAD、λEdge分别是CCensus、CAD、CEdge的变换影响参数,P(a,b)则采用以下方程计算:

P(a,b)的作用是将匹配代价归一化,使代价值投影到[0,1]范围,从而使不同代价计算方法得到的初始代价对最终代价的贡献相同。由于P(CCensus,λCensus) 、P(CAD,λAD)取值范围均为[0,1],所以融合两个初始代价时将两种方法的初始代价相加并取平均,保证初始代价范围仍然在[0,1]。
本文采用AD-Census 立体匹配[10]中的λCensus、λAD变换影响参数,λCensus取30.0,λAD取10.0。由于CEdge的值只有0 和255,所以以10 为间隔,选取0.01~100 作为λEdge的候选值,以标准立体匹配库中的4幅图像作为实验对象,实验结果如图3所示。

图3 不同λEdge 值对应的错误率
图3 中的纵坐标表示匹配精确度,横坐标表示λEdge值,从图中可以看出,当λEdge值小于等于1时,立体匹配结果对应的错误率几乎没有变化,当λEdge值大于1 时,错误率明显上升,尤其是Teddy 图像,变化最为明显。因此,在本文的实验中,λEdge取值为1。
因此最终的初始匹配代价分为两部分,当匹配区域处于边缘时,匹配代价为CEdge,当匹配区域处于非边缘时,匹配代价为CCensus、CAD的融合代价。
2.2 基于超像素自适应搜索区域的代价聚合
超像素分割方法是将具有相似纹理、颜色、亮度等特征的相邻像素聚集成不规则像素块,用来区分不同特征物体的技术,常用于目标识别、目标检测[21]、深度信息恢复[22]等计算机视觉领域。对于立体匹配得到的深度信息,利用颜色相似区域有相同的视差的原理[16],可以认为超像素体中的像素拥有相同的视差。简单线性迭代聚类方法(Simple Linear Iterative Clustering,SLIC)相对于其他超像素分割算法具有计算复杂度低的优势[21],因此在本文中,利用SLIC对图像进行超像素分割处理。不同超像素分割范围的图像如图4所示。

图4 选取不同超像素数量Teddy的分割结果
通过图4 可以发现,分割个数越多,对图像分割越精确,在图像边缘位置分割越好,但是分割时间相对较长。在超像素个数少的分割图像中,虽然分割时间较短,但由于图像边缘较多,因此会将多个深度不连续的边缘包含在一个超像素体中。在超像素分割过程中,将每一个超像素体的中心点进行标记,并将此中心点的颜色定义为超像素体内所有像素颜色的均值。

在进行代价聚合步骤时,本文汲取文献[10]中提出的基于单个像素的自适应聚合范围方法,并以此为基础,提出基于超像素的自适应聚合范围方法。该方法以每个超像素为中心,分别以超像素为单位进行条件约束下的自适应搜索。由于米字骨架需要搜索8个方向,因此搜索到的代价聚合范围更加全面。聚合范围搜索过程中用到的条件约束分别由颜色约束和距离约束组成,具体公式如下:

式中,sp 为当前超像素的中心位置,sp1为以sp 为出发点向右搜索的不同的超像素中心点(以向右搜索为例)。dn_sup为搜索的步长;τ1、τ2为设置的颜色约束阈值;L1、L2为空间距离约束阈值;Dc(sp1,sp)为超像素sp1、sp 的颜色差,Ds(sp1,sp)为超像素sp1、sp 的空间距离差。
约束条件(6)对超像素sp 和搜索到的超像素sp1,以及sp1和搜索到sp1之前的一个超像素sp1+(dn_sup,0)进行颜色约束,该约束条件的作用是防止搜索范围超出边界。约束条件(7)为对超像素sp1和sp 进行距离约束,用一个较大的值L1在无纹理和缺乏纹理区域聚集到更多的代价值。当在满足条件(6)和(7)的情况下搜索范围仍然很大时,为了节省搜索时间和保留搜索点的局部特征,定义公式(8),即当搜索距离超过L2(L2<L1)时,对超过L2的超像素实行更严格的颜色约束,使sp1与sp 的颜色差小于τ2(τ2<τ1)。具体搜索示意图如图5所示。

图5 超像素基于米字骨架自适应搜索示意图
在图5 中,第一行两幅图为中心搜索超像素图,第二行两幅图为在约束条件(6)和(7)下的基于米字骨架的搜索区域图,第三行两幅图为加上约束条件(8)的搜索区域图。从A 组图中可以看出,在加上约束条件(8)后,搜索区域明显减小,避免了在缺乏纹理和无纹理区域过多地聚合代价信息。在保留了该超像素的局部特征信息的同时,减小了在视差匹配时的误差。而在B组图中加上约束条件(8)后搜索区域没有发生变化,说明该约束条件在缺乏特征区域效果明显,而在特征较为明显区域约束性不强。
由于超像素单元中包含的像素个数较多,若在聚合时将搜索到的超像素代价值进行简单地累加,则失去了每个中心超像素的特征性。因此对于自适应搜索到的超像素,将其代价乘以权值exp(-i)(i 表示按照极线方向搜索到的第i 个超像素),以保留超像素的特征,在一定程度上提高匹配的精确度。代价聚合公式如下所示:

2.3 超像素视差优化
视差计算采用WTA(Winner Take All)策略求出粗略视差值,并利用左右一致性检查得出错误匹配视差。在视差优化步骤,本文分为两步:
(1)极线修正。先对初始视差图进行左右一致性检测。对于经过左右一致性检测得出的异常值(非遮挡点),通过搜索该异常值周围16 个方向的有效像素点,找出最具有相似特征的像素点,并将找到的正确匹配的像素点的视差值赋值给该异常点。若该异常值是遮挡点,则将其填充为周围16 个像素中视差值最低的视差值,对其进行视差修正。

式中,rx,ry,(rx,ry∈[-2,2])分别表示相对于中心点(x,y)的周围16 个方向的像素搜索,Dis(x+rx,y+ry)为该像素点周围搜索到的16个有效的视差值;Dis(x,y)代表搜索到的16个方向中颜色差异最小的像素点的视差值。
(2)超像素修正。计算每个超像素中由第一步修正后得到的视差,并将超像素中的每个像素的视差值映射到对应的直方图上。其具体步骤如下:
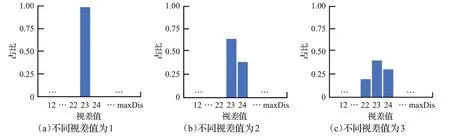
图6 超像素映射直方图
①计算视差图像每个超像素内的像素视差值,并将其投影到直方图中,其对应的直方图形式如图6 所示。本文将Tsukuba等4幅经过极线修正的视差图像进行统计,计算视差图每个超像素中对应的不同视差值,并统计不同视差值的像素个数,将其以折线图(如图7)的形式呈现出来。从折线图中可以看出,超像素中不同视差值分别为1、2、3、4个。其中不同视差值个数为1的最多,说明大部分像素正确匹配;不同视差值个数为2的大约占27%;个数为3 的大约占14%;个数为4 的最少,比例不到5%。因此,个数为1 的超像素为正确匹配,如图6(a)所示,不进行后续的优化;视差值个数为2、3、4的超像素分别进行以下2、3、4步优化。

图7 超像素内不同的视差值个数
②若超像素中的不同视差值为2,如图6(b)所示,则搜索该超像素内匹配正确的视差值,若全部为正确匹配,则不对其进行优化;若超像素内正确匹配的视差值为dc,则将该超像素内的视差值更改为dc;若超像素内没有正确匹配的视差值,则对该超像素周围像素进行搜索,找到颜色差最小的正确匹配的像素视差值ds,并将该超像素内的像素视差值更改为ds。
③若超像素中的不同视差值为3,如图6(c)所示,先搜索超像素内正确匹配的视差值,若全部正确匹配,则不对该超像素视差值进行处理;若有正确匹配的像素视差值,则对超像素内没有正确匹配的像素视差值进行更新,更新准则为:若未匹配像素视差值与匹配像素视差值颜色差小于λcolor,则对像素视差值进行更新,否则标记该像素为误匹配,进行下一次更新.
④若超像素中的不同视差值为4,先搜索超像素内正确匹配的视差值,若全部正确匹配,则不对该超像素视差值进行处理,否则进行与第③步相同的步骤进行视差更新。
2.4 算法伪代码
基于上文对本文算法各步骤的详细描述,给出以下算法伪代码。其中Ileft、Iright分别表示输入左右目图像,N 表示超像素个数,min Dis、max Dis 分别表示最小最大视差,d 表示视差取值,DleftDright表示视差图。
输入:左右图像、超像素个数、最小最大视差。
1. Ileft和Iright进行SLIC超像素分割
2. for d in min Dis to max Dis,do
3. Ileft和Iright计算AD、Census、Edge代价
4. # parallel compute {
5. for 每个超像素in Ileft和Iright,do
6. 基于米字骨架计算聚合范围
7. 基于聚合范围代价聚合
end}
end
8. WTA求出DleftDright
9. for DleftDright,do
10. LRC左右一致性检测
11. if 错误点为非遮挡点
填充具有相似特征的像素对应的视差
12. else
填充周围16个像素中视差值最低的视差值
13. LRC左右一致性检测
14. for每个超像素in DleftDright,do
15. 利用直方图统计不同视差值个数
16. 根据不同视差值个数的情况进行不同步骤的优化操作
end
end
输出:最终的视差图DleftDright。
3 实验结果与分析
本文算法在Windows平台下采用C++语言在Visual Studio 2015 环境下进行开发实现,硬件条件为Intel Core i7-4790 CPU,频率为3.6 GHz,实验平台为Visual Studio2015 和OpenCV3.2.0。检验算法性能的图像来源于Middlebury 网站提供的数据集[23],先选取4 组图像对初始视差进行求取。本文算法采用超像素个数为3 200,其他的参数设置如下:

3.1 初始视差结果求取与分析
如图8 为对Tsukuba、Venus、Teddy、Cones 这4 幅图求取的初始视差结果,Census算法在低纹理区域出现了大面积匹配错误的现象,如Tsukuba的灯罩区域;AD算法在边缘部分较Census算法表现较好,例如Teddy的桌子边缘区域,但在纹理丰富区域,例如Cones 的木板区域,以及Teddy 的背景区域,却没能达到正确匹配的效果。而本文的方法结合两种方法的优点,无论是在低纹理区域还是在边缘区域,都能够得到较精准的视差。
3.2 视差结果与分析
如图9为各算法分别对Tsukuba、Venus、Teddy、Cones这4 幅图求取的视差结果。其中图9(a)、(b)分别是基准图像及标准视差图;图9(c)、(d)、(e)、(f)分别是ADCensus算法[25]、FA算法[26]、ASW算法[27]、GMM-MST[28]算法得出的立体匹配结果;图9(g)为利用本文算法得出的立体匹配结果。

图8 经过代价计算的初始视差图
表1根据Middlebury Stereo Evaluation对求出的视差结果进行测试,给出了立体图像对求得的视差图在非遮挡区域(noncc)、视差不连续区域(disc)、所有区域(all)在错误阈值为1.0 时的匹配错误率,可以看出本文除了Tsukuba 匹配效果不是很好,在另外3 张图中相对于另外4 种方法都减少了立体匹配的错误率。其中ASW 以及GMM-MST 算法在Tsukuba 匹配上分别优于本文算法0.55、0.61 个百分点,本文算法比AD-Census、FA 算法分别降低了0.75、0.31 个百分点。在Venus 上,本文算法相对于4 种算法中表现最好的GMM-MST 算法,错误率降低了0.05 个百分点。在Cones 上,本文算法较AD-Census算法错误率降低了1.41个百分点,相对于ASW 算法降低了3.41 个百分点。本文算法在Teddy上表现最好,匹配精度明显增加,相对于AD-Census、FA算法分别降低了6.2、4.6个百分点。
3.3 算法性能分析
在初始代价计算步骤,本文通过计算AD、Census、Edge得到初始代价,令N 为图像像素个数,L 为视差取值范围,则匹配代价计算步骤的时间复杂度为O(NL)。通过SLIC 算法对图像进行超像素分割,时间复杂度只与像素的数量线性相关,为O(NL)。在代价聚合步骤,本文算法可在保证视差结果不变的情况下,利用OpenMP对聚合范围求取步骤和初始代价聚合步骤并行加速,加快程序运行速度。若超像素个数为M ,则聚合步骤在不利用并行加速的条件下时间复杂度为O(ML)。通过超像素对视差进行优化,若只计算最差情况下即所有超像素都需要进行修正的情况下,时间复杂度为O(ML)。因此本文算法运行速度跟图像的大小和分割的超像素的个数成正比,图像过大或分割的超像素个数过多,会使运行速度变慢。

图9 不同算法得到的视差图

表1 阈值为1.0时不同算法的错误匹配率%
本文对大小为450×375的图像进行处理,在加上并行运算的条件下,运行时间为230 ms。表2为本文算法与GMM-MST 算法、FA 算法、文献[15]的运行时间对比。GMM-MST 算法由于在求解GMM 模型时需要将图像分割为多个区域并需要多次迭代求解,因此所需时间相对于其他三种算法较长。本文算法在平均运行时间上较FA算法和文献[15]算法要短,并且与文献[15]基于强相似点算法相比较,本文算法在匹配结果精度上更高。

表2 运行时间对比ms
为了验证本文算法在不同图像上的适应性,对Middlebury标准测试平台[23]提供的标准图Aloe、Baby、Bowling进行了测试,视差搜索范围分别为[0,60],[0,52],[0,67]。图10(a)为标准测试图,图(b)为标准视差图,图(c)为本文算法得到的视差结果。通过与标准视差图作对比,本文算法在重复纹理区域以及缺乏纹理区域得到了很好的匹配效果。利用本文算法得到的aloe立体匹配结果图,在前景颜色与背景颜色极为相似的地方,由于在图像分割过程中出现误分割,匹配效果不是很好,是下一步需要改进的地方。

图10 本文算法测试结果
4 结论
本文提出一种融合边缘信息的多特征融合代价计算方法和结合超像素的代价聚合、视差优化立体匹配方法。通过在代价计算步骤中加入边缘信息代价,提高了在深度不连续区域的辨识度,进而增加了立体匹配的精确度。通过结合SLIC 超像素分割,在代价聚合步骤中利用米字骨架自适应搜索超像素,得出聚合范围,并且分割得到的超像素可用来对误匹配视差进行优化,提高匹配精度。
实验结果表明,本文算法能有效处理缺乏纹理和重复纹理区域的深度信息,并且在深度不连续区域得到了有效的匹配,但在前景颜色与背景颜色较为相近的区域,由于容易引起错误分割,导致在此区域匹配效果不是很好,是下一步算法需要改进的地方。由于本文算法在代价聚合步骤可以进行有效的并行运算,因此,通过GPU 并行编程技术实现本文算法是下一步的工作方向。

