求解物流配送中心选址问题的蜘蛛猴算法

徐小平，杨 转，刘 龙

1.西安理工大学 理学院，西安710054

2.西安理工大学 自动化与信息工程学院，西安710048

1 引言

随着互联网的兴起，物流产业也得到了快速地发展，物流配送中心的选址设计和优化方案显得格外重要。在物流系统中，配送中心的选址是指在一个具有若干供应点及若干需求点的范围内选择一定数量的地点来设置配送中心的优化过程[1]。配送中心在供货点与用户之间发挥着良好纽带的作用，属于物流系统中的一个关键环节，它决定着物流的配送距离、成本及配送模式，进而影响物流产业的效率[2-4]。因此，研究物流配送中心选址问题具有重要的意义。然而，物流配送中心选址问题涉及的变量及约束条件非常多，属于典型的NP 难问题[5]，以至于一些传统的方法难以解决该问题。目前，已有许多学者利用群智能算法对该问题进行了研究，如：差分进化算法（Differential Evolution，DE）[6]、粒子群算法（Particle Swarm Optimization，PSO）[7]、猴 群 算 法（Monkey Algorithm，MA）[8]等。但是这些算法普遍存在过早地局部收敛，求解精度不高等缺点。

2014年，Banasal等人模拟自然界中蜘蛛猴的觅食行为提出了蜘蛛猴优化算法（Spider Monkey Optimization，SMO）[9]，基于蜘蛛猴的裂变融合社会结构这一特点，将该算法抽象为局部和全局更新机制。其突出特点在于敏感参数少，鲁棒性强且具有良好的全局收敛性，尤其在求解多峰、多维复杂函数中有较好的效果。目前，该算法已应用到压力容器设计[10]、灰度图像[11]及伦纳德-琼斯[12]等诸多问题中。但是在解决具体问题时，基本蜘蛛猴算法存在求解精度不高的缺点。因此，有必要对蜘蛛猴算法进一步改进来提高寻优性能。

2 物流配送中心选址模型

物流中心选址问题是指：在有限个数量的位置中，选取一些地点作为配送中心，并为所有位置提供货物，使得在满足供应各个位置所需的要求下，总成本最低。因此，本文作如下假设：（1）配送中心必须满足所有位置的需求；（2）每个需求点有且只能由一个配送中心进行供应；（3）不考虑其他费用。基于上述假设，其目标是使各位置的需求量到与之最近配送中心的距离的乘积之和最小，由此可建立如下模型。

其中，目标函数min F 表示被选中的物流中心j 到由它配送的位置i 的需求量与距离乘积之和的最小值；是所有位置的编号集合；k 为被选中的物流中心j 到由它配送的位置i 的最大距离；Mi表示其余位置到物流中心的距离小于k 的备选物流中心的集合；hi表示位置i 的需求量；dij表示位置i 到离它较近的物流中心j 之间的距离；zij是0-1 变量，当zij为1时，表示物流配送中心j 将为位置i 供货物；ej表示位置点和物流中心之间的需求分配关系，ej也是0-1 变量，当ej为1 时，表示位置i 被选为物流中心；r 为被选中的物流中心数量。

3 蜘蛛猴优化算法及其改进

3.1 基本蜘蛛猴优化算法（SMO）

基本蜘蛛猴算法具体如下：

（1）解的表示和初始化设Xi=(xi1,xi2,…,xin) 为目标函数的一个可行解，表示第i 只蜘蛛猴当前的位置，由下式生成：

其中，i=1,2,…,P，P 表示群体规模，Xij表示第i 只蜘蛛猴在第j 维的分量，Xminj和Xmaxj分别为第j 维的下限和上限，j=1,2,…,n，n 为优化问题的维数，是上均匀分布的随机数。

（2）局部领导阶段

该过程是每个蜘蛛猴在自己的局部小范围内通过迭代寻找优化问题的目标函数值的过程，蜘蛛猴基于局部领导者以及小组其他成员的经验来更新当前位置。若新位置适应度值优于原来位置适应度值，则蜘蛛猴就更新到新位置，具体过程如下：

其中，LLkj是第k 个局部群体领导者在第j 维的分量，Xrj是随机地从第k 个群体中选出的第r 个蜘蛛猴的第j 维分量( r ≠i )，R( 0,1) 是[0 ,1] 上均匀分布的随机数，R( -1,1) 是[- 1,1] 上均匀分布的随机数，k ∈[1 ,MG ]，MG 为最大组数。

（3）全局领导阶段

在这一阶段，蜘蛛猴基于全局领导者以及局部小组成员的经验来更新其位置，且蜘蛛猴位置更新受到概率值probi的约束，如果rand( )＜probi，则进行以下的更新：

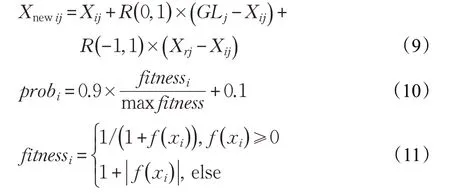
其中，GLj是全局领导者在第j(j ∈1,2,…,n) 维的分量，fitnessi表示第i 个蜘蛛猴对应的适应度值，max fitness 表示最大的适应度值，为相应的目标函数值。

（4）全局领导学习阶段

全局领导者运用贪婪选择过程来更新其位置，将整个种群中具有最大适应度值的蜘蛛猴选为全局领导者；检查全局领导者的位置是否更新，如果位置没有更新，则全局限制计数增加1。

（5）局部领导学习阶段

局部领导者运用贪婪选择过程来更新它们的位置，将每个局部群体中具有最高适应度值的蜘蛛猴选为局部领导者；如果局部领导者的位置没有更新，则局部限制计数( )

llc 增加1。（6）局部领导决策阶段如果局部领导者的位置在预先决定的迭代次数没有更新，即llc 达到了局部领导限制( )lll ，那么该组中的所有成员基于扰动率( )pr 的大小用式（1）的随机初始化或用下式来更新位置：

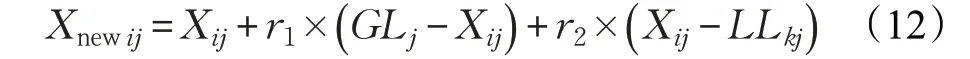
其中，r1和r2是[ ]0,1 上均匀分布的随机数。

（7）全局领导决策阶段

如果全局领导者的位置在预先决定的迭代次数没有更新，即glc 达到了全局领导限制( )gll ，那么将整个群体进行分组。每次执行该阶段时，也会启动局部领导学习阶段，用来选取新建小组的局部领导者。将群体分组直到达到MG，又重新组成一个群体，即MG=1。

通过以上过程使得蜘蛛猴群不断更新位置，直至目标函数在连续迭代的优化值没有变化，或到达预先设定迭代次数，则算法终止，输出最优位置和最优函数值。

3.2 基于Laplace 分布的伪反向蜘蛛猴优化算法（LOBSMO）

基本蜘蛛猴算法中蜘蛛猴的位置更新在局部领导阶段、全局领导阶段及局部领导决策阶段进行，这三个阶段的目的是控制算法的搜索精度。为了提高基本蜘蛛猴算法优化性能，这里在算法的解初始化及以上三个阶段提出了如下的改进思想。

（1）初始化的改进

蜘蛛猴的初始化位置会对最优结果产生一定的影响，初始化位置分布越均匀，越有利于搜索到最优结果。相比较均匀分布产生随机数的方法，使用Laplace分布产生随机数更有利于探索搜索空间，发现新的潜在解，因此，该策略可以保证搜索空间的多样性，避免陷入局部最优，逐渐向全局最优解靠近。故采用Laplace 分布的方法来产生蜘蛛猴群的初始位置，具体由如下函数来产生随机变量，Laplace分布的概率密度函数为：

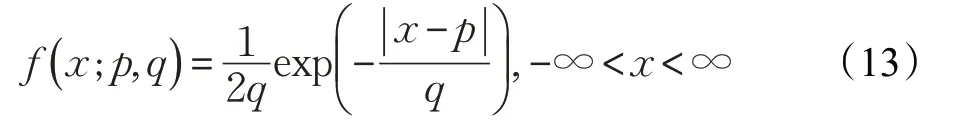
分布函数为：

从而：

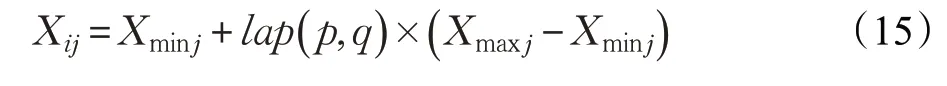
其中，lap( p,q )是Laplace 分布，p ∈( -∞,∞)是位置参数，q ＞0 是尺度参数，函数f 始终关于p 对称，且在[0 ,p] 上递增，在[ p,∞]上递减。如图1为Laplace分布和均匀分布200次迭代生成随机数的曲线比较，直观地得出：使用Laplace 分布产生随机数更有利于探索搜索空间，有助于找到潜在解。

图1 拉普拉斯分布和均匀分布生成随机数的比较

（2）局部领导阶段的改进

局部领导阶段中是由随机数产生的步长，这种步长时大时小，具有不确定性。在觅食过程中，步长越大，有利于提高算法全局探索能力，但会降低寻优精度，可能会出现振荡现象；步长越小，强调算法局部开发能力，有利于提高寻优精度，但搜索速度会降低。针对这个问题，现采用指数递减与随机对数递减分段的步长取代随机步长，使步长具有自适应性，有效平衡了全局探索能力与局部开发能力，具体更新公式如下：

从而改进后的位置更新公式为：

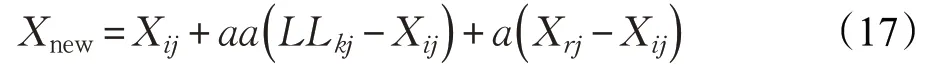
其中，A=0.5×rand( ).G 表示当前的迭代次数，N 表示总的迭代次数，amax和amin分别是步长的最大值和最小值。

（3）全局领导阶段的改进

拟改进全局领导阶段的位置更新方程，算法本身的搜索方式会对收敛速度及寻优精度有一定的影响，为了避免算法过早收敛及使蜘蛛猴快速收敛到全局最优解，故在全局领导阶段改变搜索方式，直接由全局领导者引导觅食，提高了算法的收敛速度；同时，为进一步平衡算法的搜索速度与收敛精度，加入了动态学习因子：

从而改进后的搜索方式为：

其中，zmax、zmin分别是学习因子的最大和最小值，z0为平衡因子，fi表示第i 个蜘蛛猴的目标函数值，fmax、fmin分别表示目标函数值的最大值、最小值。

（4）局部领导决策阶段的改进

在局部领导决策阶段，随着算法的不断进化，当前的局部最优解越来越接近全局最优解，那么对算法的局部搜索能力要求就越高。而该阶段蜘蛛猴群的位置是不断变化的，毫无规律，具有很大的随机性，不利于在局部小范围内寻找最优解。为了克服这个缺点，引入伪反向学习策略来产生伪反向种群，增加了种群的多样性，这样蜘蛛猴群能够在局部小范围内进行精细搜索，避免了跳过最优解的弊端，然后从当前种群和伪反向种群进行精英选择，从而有效地找到最优解。具体过程如下：

根据概率论，有50%的反向解会更优。因此，基于当前解和反向解，反向解具有加速收敛并提高算法精度的潜力。

若伪反向解的适应度值优于当前解的适应度值，则用伪反向解QOX 替换当前解X ；否则，当前解X 保持不变。这样，在用式（12）更新蜘蛛猴群位置之前利用上述伪反向学习策略产生全局领导者的位置，以便于更精确地找到最优解，从而提高了算法的寻优性能。

3.3 数值实验与分析

为了验证所给LOBSMO 的有效性，选取了9 个经典测试函数进行性能测试。

（1）Sphere函数：

（2）Ellipsoidal函数：

（3）Griewank函数

第二个乐段（B段）就像是一首劳动大军的进行曲，调性转为C大调。右手好像是三个声部的劳动者的合唱，左手是强而有弹性的节奏衬托。音乐雄强，气势宏大，这是李树化钢琴曲中最雄强有力的作品。

（4）Ackley函数：

（5）Zakharov函数：

（6）Levi Montalvo 2函数：

（7）Alpine函数：

（8）Levi Montalvo 1函数：

（9）2D tripod函数：

以上9个测试函数的理论最优值均为0，其中f1、f2为单峰函数，f3～f7为多峰函数，f8、f9为复合函数，在20维的情况下进行仿真实验。表1给出了LOBSMO在9个测试函数独立运行50次得到的最优值、平均值及标准差。为了说明改进算法的优越性，将LOBSMO 与文中所提的DE[13]、PSO[14]、MA[15]及SMO[9]进行了比较，结果如表1。且各算法的参数设置如下，DE：杂交概率CR=0.5 ，变异概率F=0.1 ；PSO：学习因子c1=c2=1.496 ，惯性权重最大值wmax=0.9 ，惯性权重最小值wmin=0.2，速度最大值vmax=6；MA：步长a=0.1，视野长度b=0.5 ，跳区间[c ,d ]=[- 1,1] ，爬的迭代次数Nc=10；SMO：MG=5，gll=50，lll=1 500，pr=0.8；LOBSMO：pr=0.4，p=1，q=2，amax=0.8，amin=0.5，zmax=0.8，zmin=0.5，z0=0.5。其他参数与SMO相同，5 种算法种群规模都设为50。总迭代次数为1 000，在20维情况下进行测试。

根据表1各项结果得出：LOBSMO对于f2、f3和f9的求解结果达到了理论最小值0。对于f5，PSO的标准差为0，但其最优值和平均值都为1 000，说明每次求解的值都很大，精度低。除了f5，LOBSMO对每个测试函数求解的最优值、平均值和标准差都优于DE、PSO、MA及SMO。因而，所提的改进策略效果较优。图2 展示了5 种算法关于f1、f8的收敛曲线图，从图中可看出：LOBSMO的收敛精度明显优于其他4种算法。

表1 LOBSMO与对比算法关于测试函数的结果

图2 5种算法的收敛曲线图

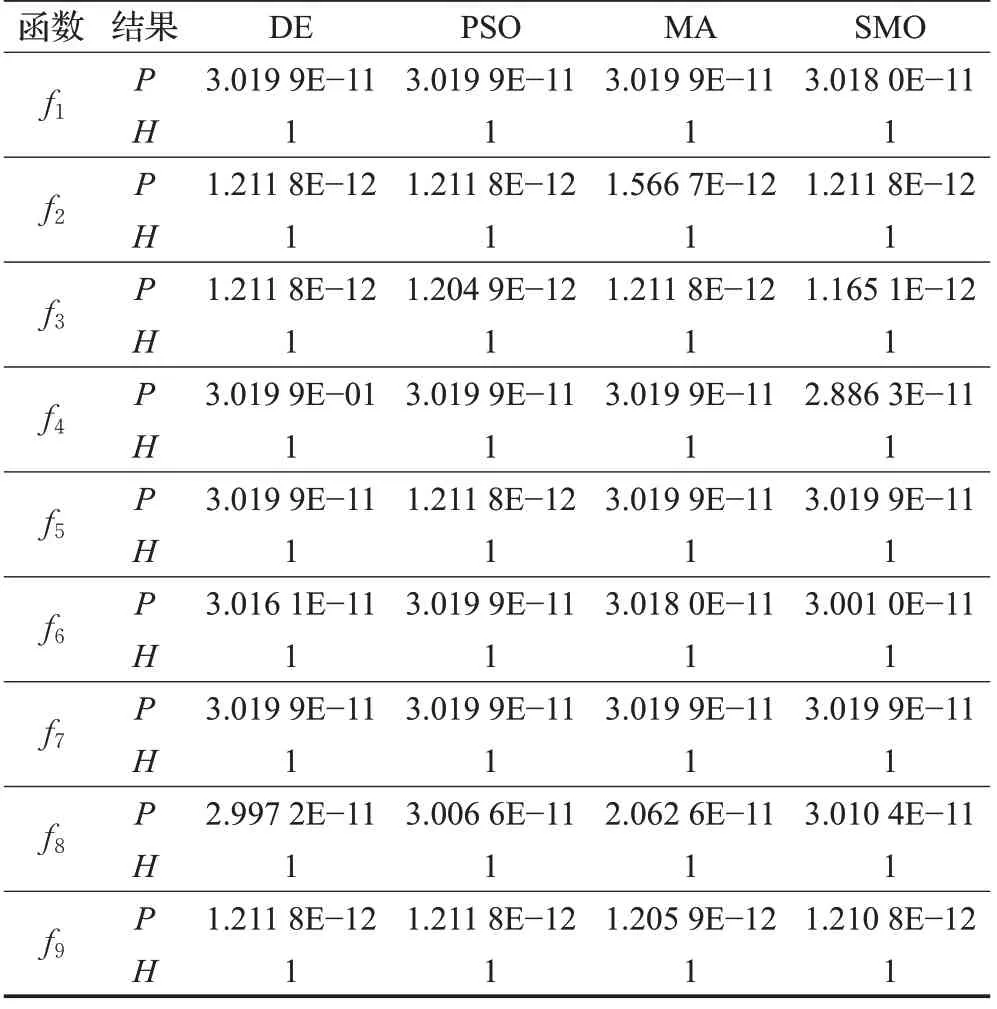
表2 LOBSMO与4种算法的Wilcoxon秩和检验结果

由表2的P 和H 值可总结出：对于全部9个测试函数，LOBSMO 与SMO、MA、PSO、DE 的Wilcoxon 秩和检验结果中，H=1 说明每两组数据都有显著差异，P值都小于1×10-10，并且LOBSMO 的精度高，因此，LOBSMO 优于所对比的算法，其寻优性能得到了很大的改善。

4 改进的蜘蛛猴算法求解物流中心选址问题

4.1 求解步骤

利用改进的蜘蛛猴优化算法求解物流配送中心选址问题，就是以式（1）为目标函数，寻找其最小值。在求解过程中，它们的对应关系为：算法中每个蜘蛛猴的位置对应求解问题的一组可行解，种群规模对应备选的方案数目，搜索空间的维数对应备选的城市个数，选出全局领导者的位置对应配送中心。具体求解步骤如下：

步骤1 设定蜘蛛猴算法的参数值，如种群规模P，总的迭代次数N 等参数。

步骤2 用round( )函数对式（15）中的分量取整，给出种群中每个蜘蛛猴的初始位置。计算出蜘蛛猴群中个体当前位置的适应度值，找出当前最优的位置及对应的适应度值并记录，将每个小组中适应度值最优的蜘蛛猴选为局部领导者后，将局部领导者中具有最优适应度值的猴子选为全局领导者。

步骤3 执行局部领导阶段，用分段步长式（16）取代随机步长。根据式（17）不断进行觅食，计算该阶段位置更新后，蜘蛛猴群中个体当前位置的适应度值，如果有更好的适应度值，则更新蜘蛛猴群位置到较好适应度值相对应的位置。

步骤4 执行全局领导阶段，由式（19）产生新的蜘蛛猴位置，向全局领导者位置靠近。

步骤5 依次执行全局领导学习阶段、局部领导学习阶段，判断全局和局部领导者的位置是否更新，如果全局领导者的位置没有更新，则glc 增加1；如果局部领导者的位置没有更新，则llc 增加1。

步骤6 执行局部领导决策阶段之前，用伪反向学习策略式（20）、（21）产生全局领导者，再根据式（12）继续更新蜘蛛猴的位置，计算蜘蛛猴群中个体当前位置的适应度值，如果有更好的适应度值，则更新蜘蛛猴群位置到较好适应度值相对应的位置。

步骤7 执行全局领导决策阶段，判断glc 是否达到了gll ，如果达到则将整个大群体进行分组，即局部群体数增加1；群体分组直到达到MG ，又重新组成一个群体，即MG=1。

步骤8 重复步骤3～7，直至满足终止条件，算法结束，输出最优位置和最优适应度值，即得到物流中心的城市位置编号和最优值。

4.2 仿真实验

这里采集了中国31 个城市的坐标，从中选出6 个配送中心。如表3 为城市坐标和所需配送的货物量，表中，( x,y )代表中国31个城市的坐标，hi表示各城市的需求量。

表3 31个城市的位置及其对应的需求量

用LOBSMO 求解该问题时，算法参数设置与3.3节中数值实验与分析的参数相同。用LOBSMO 求解一次31 个城市的物流中心选址问题，得到的最优值为5.496 5E+005，选出的配送中心为5-9-12-17-20-27。接着，利用DE、PSO、MA 及SMO 进行一次求解得到的最优值分别为6.860 9E+005、6.205 2E+005、5.827 2E+005、6.014 4E+005；相应的配送中心分别为8-11-16-17-21-26，1-2-3-4-5-7，3-5-9-14-20-27，5-9-14-19-22-28。这5种算法求解过程收敛曲线如图3所示。进一步利用5个算法分别对31 个城市物流选址问题进行50 次求解，得到的最优值、平均值、中位数和标准差如表4所示。

图3 对31维物流中心选址寻优曲线图

为了进一步说明LOBSMO 的有效性，收集了中国100 个城市的坐标，要选出21 个物流配送中心。如表5为各城市具体的坐标及对应的货物量。利用以上5 个算法分别求解这100 个城市的物流中心选址问题，LOBSMO、DE、PSO、MA 及SMO 求解的最优值分别为1.077 3E+006、1.206 7E+006、1.202 6E+006、1.109 5E+006、1.127 7E+006；求解的物流配送中心分别为4-5-9-12-16-21-27-33-37-47-55-58-59-63-73-75-80-90-93-94-99，1-7-12-27-29-31-43-48-52-60-63-64-67-72-78-80-87-89-94-96-10，1-2-3-4-5-6-7-8-9-10-11-12-13-14-15-16-17-18-19-20-21，4-10-14-22-29-32-36-37-43-46-47-49-55-56-61-72-75-80-86-97-99，1-3-4-10-11-15-22-24-25-27-30-37-51-58-66-74-75-80-81-91-94。求解过程的收敛曲线均如图4所示。用5种算法分别进行50次求解，其最优值、平均值、中位数和标准差仍如表4所示。

表4 5种算法求解31维及100维选址问题的结果

从对31个和100个城市的仿真结果可得出：LOBSMO都能求解到最优值，即需求量与运输距离乘积之和的最小值。SMO、MA 的求解效果次之，DE 寻优结果最差。同时LOBSMO得到的平均值、标准差都最小，说明每次的求解结果都比较接近而且较优，具有一定的鲁棒性。且由图3及图4可看出，LOBSMO可以快速地求解到最优值，说明了该改进算法有效地平衡了求解精度与收敛速度之间的关系。

图4 100维物流中心选址寻优曲线图

箱型图[17]是用来说明一组数据分散程度情况的统计图。为了更直观地观察LOBSMO 的优越性，将5 种算法分别求解31维及100维实例得到的50次结果用箱型图展示出来，如图5及图6所示。

表5 100个城市的位置及其对应的需求量

图5 31维物流配送中心选址问题的箱型图

图6 100维物流配送中心选址问题的箱型图

由图5及图6可得出，LOBSMO求解不同维度的实例50次得到的最大值、最小值（图中黑色横线）及中位数（图中红线）都优于SMO、MA、PSO及DE，而且LOBSMO具有最小的高度。MA的寻优结果次之，DE高度最大，故其效果最差。因而，改进蜘蛛猴算法的优化性能有了明显提高。

5 结束语

针对蜘蛛猴优化算法求解物流中心选址问题效果不佳这一问题，本文提出了基于Laplace 分布的伪反向蜘蛛猴算法来求解该问题。首先，在基本蜘蛛猴算法中，用Laplace分布产生随机数来初始化蜘蛛猴群，增加了初始种群的多样性。在局部领导阶段，采用非线性递减分段的步长，有效平衡了全局探索与局部开发能力。改变了全局领导阶段的觅食方式，加快了收敛速度。局部领导决策阶段引入伪反向学习策略，避免算法陷入局部最优。通过9个测试函数和Wilcoxon秩和检验，说明所提改进算法是可行的。然后，利用改进算法分别求解31维及100维的物流中心选址问题。最后，结合所求结果及箱型图验证了该算法的优越性，为解决多维复杂优化问题提供了一种有效的方法。