基于NFSR的分组密码算法SPRING*

田甜,戚文峰,叶晨东,谢晓锋

战略支援部队信息工程大学,郑州450000

1 SPRING算法概述

SPRING是基于非线性反馈移位寄存器设计的轻量级分组密码,采用SP结构[1],支持的分组长度/密钥长度参数为128/128、128/256和256/256.SPRING-n-m表示分组长度为n且密钥长度为m的分组密码算法.SPRING-128-128的迭代轮数为10轮,SPRING-128-256的迭代轮数为14轮,SPRING-256-256的迭代轮数为18轮.为了算法描述的一致性,以下记算法迭代轮数为Nr∈{10,14,18},由分组长度/密钥长度决定具体取值.SPRING-n-m系列加密算法和解密算法的设计框架参见算法1和算法2,其中加密算法ENCRYPTION包含密钥扩展算法KeyExpansion、轮函数Round、最后一轮轮函数FinalRound,解密算法DECRYPTION与加密算法具有相似性,也包括密钥扩展算法InvKeyExpansion、轮函数InvRound、最后一轮轮函数Inv FinalRound.

算法1 ENCRYPTION 算法2 DECRYPTION Inp ut:plaintext,key Outp ut:ciphertext 1 state←plaintext；2(rk1,rk2,···,rk Nr+1)=KeyExpansion(key)；3 for 1≤i≤Nr-1 d o Inp ut:ciphertext,key Outp ut:plaintext 1 state←ciphertext；2(RKin v 1,RKi 2nv,···,RKi N n r v+1)=InvKeyExpansion(key)；3 for 1≤i≤Nr-1 d o 4 Round(state,rk i)；5 end 6 FinalRound(state,rk Nr,rk Nr+1)；7 ciphertext←state；4 Inv Round(state,RKi i n v)；5 end 6 Inv FinalRound(state,RKin v ,RKin v)；N r N r+1 7 plaintext←state；

2 SPRING-128-128的设计

本节介绍SPRING-128-128的具体设计参数.

2.1 SPRING-128-128的内部状态

SPRING-128-128的内部状态以字节为单位,看作F28上的16维向量或者F28上4×4的矩阵,即

其中si为一个字节,即8比特,0≤i≤15.以下内部状态矩阵总是记为

设128比特的明文分组为plaintext=p0‖p1‖···‖p15,其中pi是一个字节,0≤i≤15,则用明文填充内部状态的规则为

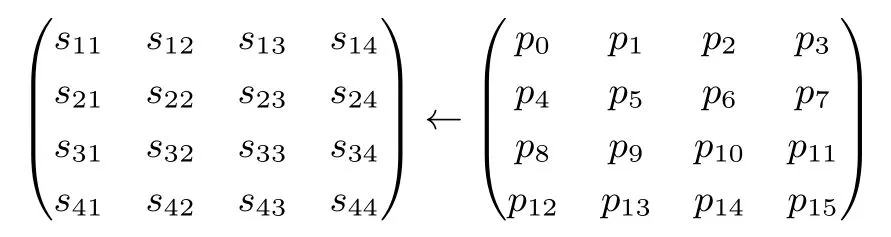
设一个128比特密文分组为ciphertext=c0‖c1‖···‖c15,其中ci是一个字节,0≤i≤15,则内部状态与输出密文分组的对应关系为

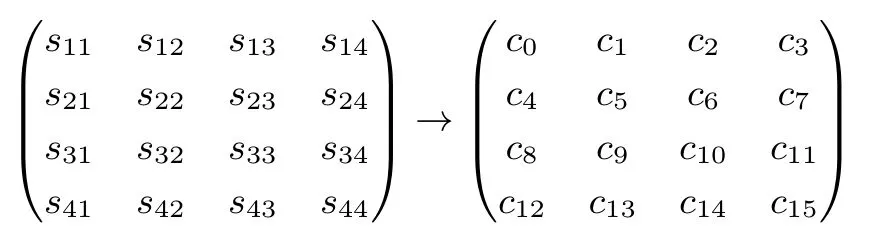
2.2 SPRING-128-128加密算法

SPRING-128-128算法的迭代轮数为10轮,即Nr=10.SPRING-128-128加密算法轮函数Round-128包括三个子函数:AddRoundKey,SubRow和Transpose.在每一轮轮变换中,首先加轮子密钥,然后对内部状态矩阵的每一行分别做SubRow运算,最后对内部状态进行一次转置,参见算法3.

SPRING-128-128最后一轮轮函数FinalRound-128包括三个子函数:AddRoundKey,SubRow和BitPermutation,其中在SubRow运算前后各做了一次AddRoundKey,参见算法4.

算法3 Round-128算法4 FinalRound-128 Inp ut:state,rk i 1 AddRoundKey(state,rk i)；2 for 1≤j≤4 d o Inp ut:state,rk Nr,rk Nr+1 1 AddRoundKey(state,rk Nr)；2 for 1≤j≤4 d o 3 SubRow(sj1,sj2,sj3,sj4)；4 en d 5 Transpose(state)；3 SubRow(sj1,sj2,sj3,sj4)；4 end 5 AddRoundKey(state,rk Nr+1)；6 BitPermutation(state)；

综合上述定义,SPRING-128-128加密算法的整体结构参见图1,其中plaintext=p0‖p1‖···‖p15是输入明文分组,ciphertext=c0‖c1‖···‖c15是输出密文分组.

2.2.1 AddRoundKey的定义

AddRoundKey完成对内部状态与轮子密钥异或加的功能.设AddRoundKey的输入内部状态为

输入轮子密钥为

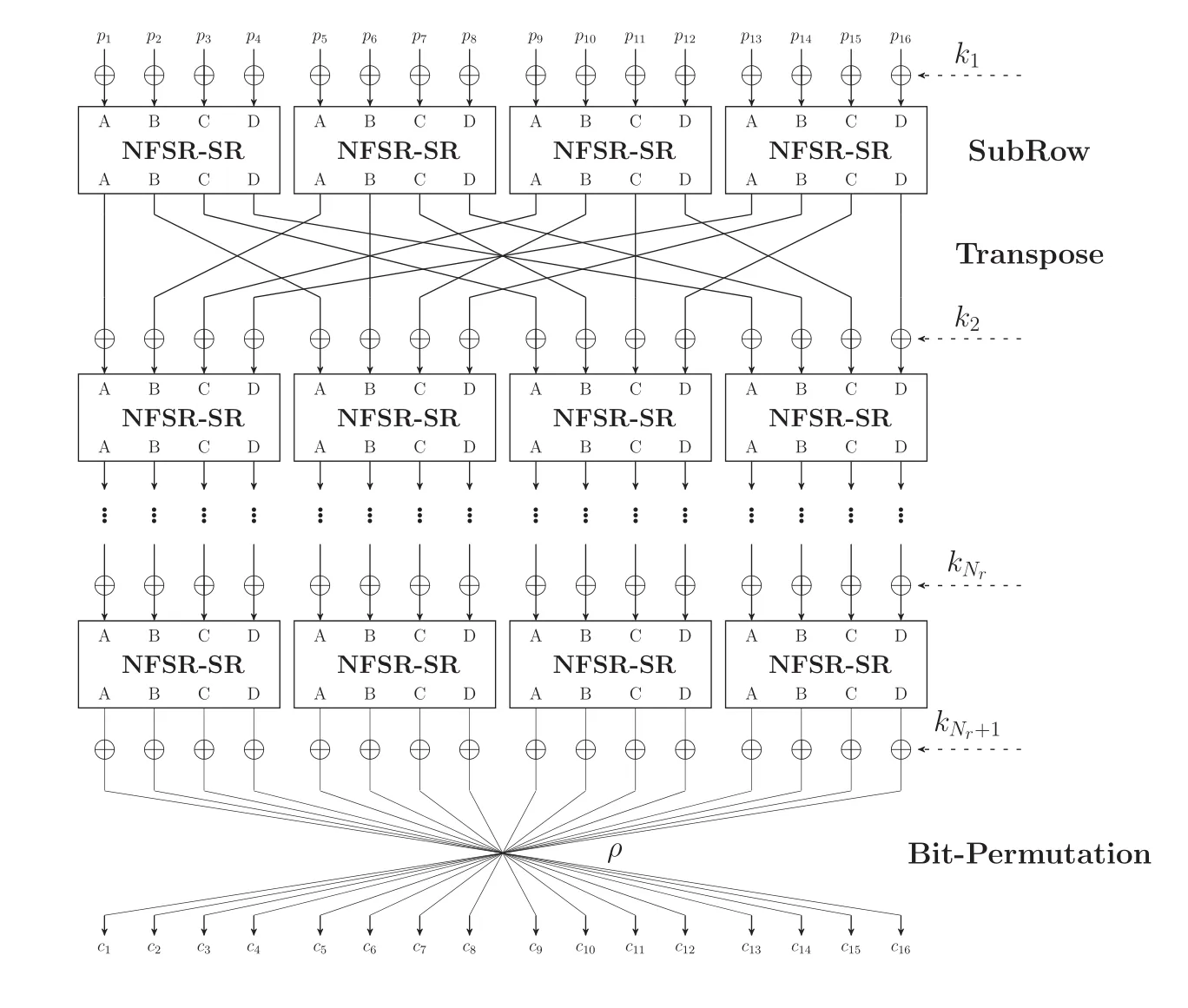
图1 SPRING-128-128加密算法示意图Figure 1 An overview of SPRING-128-128 encryption algorithm

那么AddRoundKey的计算规则为

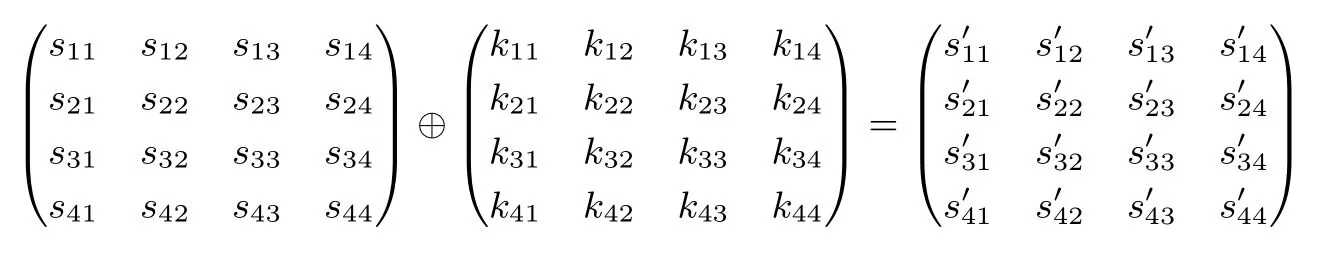
2.2.2 SubRow的定义

2.2.3 NFSR-SR设计参数

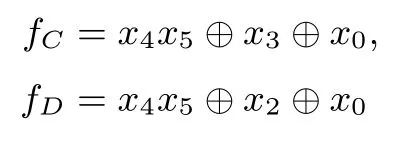
NFSR-SR是一个32比特的非线性反馈移位寄存器,可看作4个8-bit寄存器A、B、C、D互相反馈的环状串联结构,如图4所示,其中4个寄存器A、B、C、D的反馈函数分别为

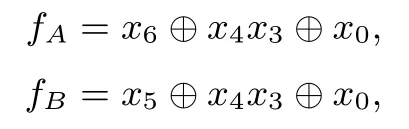
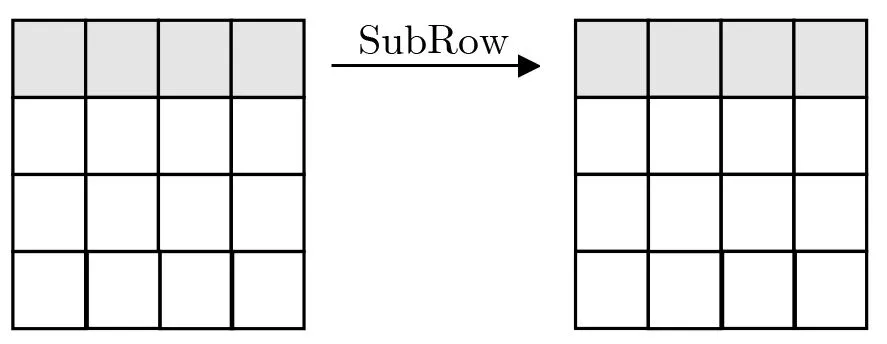
图2 SubRow示意图Figure 2 Overview of SubRow

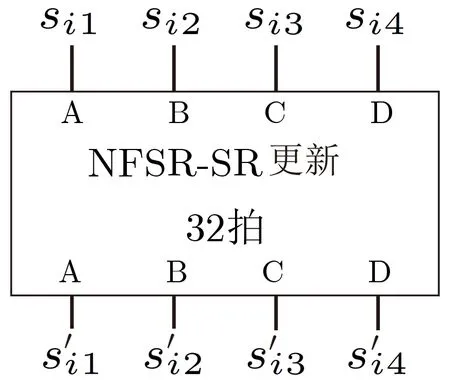
图3 SubRow(si1,si2,si3,si4)示意图Figure 3 SubRow(si1,si2,si3,si4)with an input

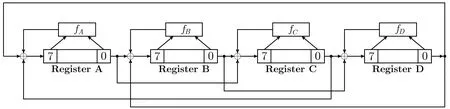
图4 NFSR-SR示意图Figure 4 An overview of NFSR-SR

为了描述的清晰性,下面给出32比特NFSR-SR的状态转移函数.设t时刻NFSR-SR的内部状态为

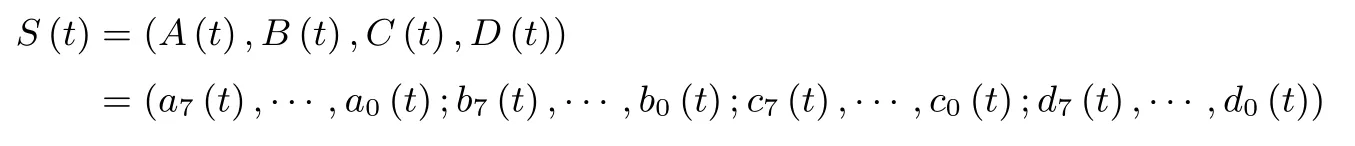
则第t+1时刻的状态为

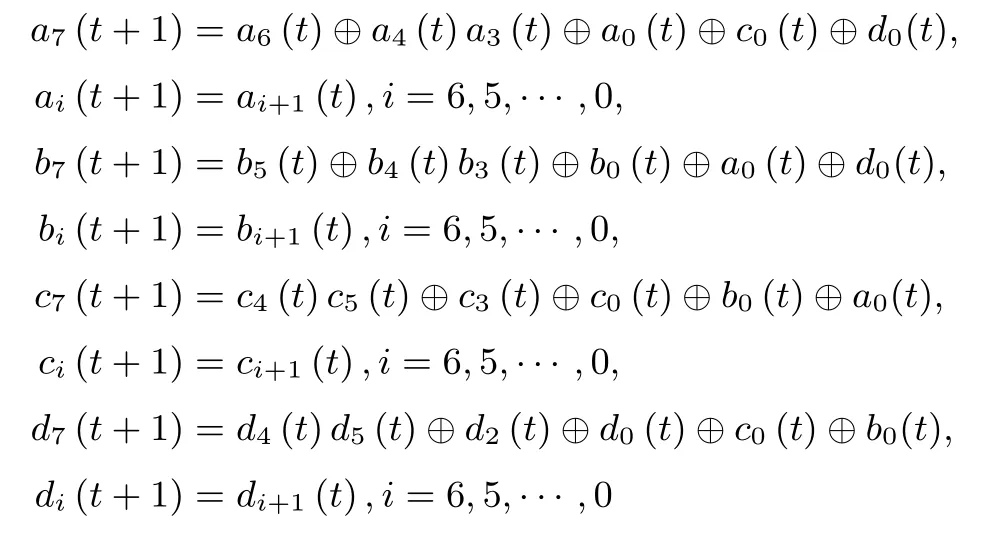
可以证明NFSR-SR的内部状态更新函数是可逆的.

命题1非线性反馈移位寄存器NFSR-SR的内部状态更新函数是可逆的.

证明：这里我们直接给出状态更新函数的逆映射.设已知第t+1时刻内部状态S(t+1)=(A(t+1),B(t+1),C(t+1),D(t+1)),并记

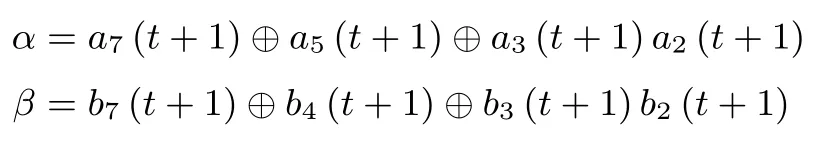
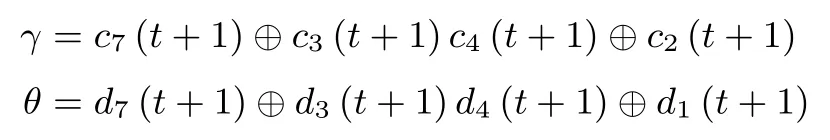
下面给出第t时刻内部状态S(t)的计算公式

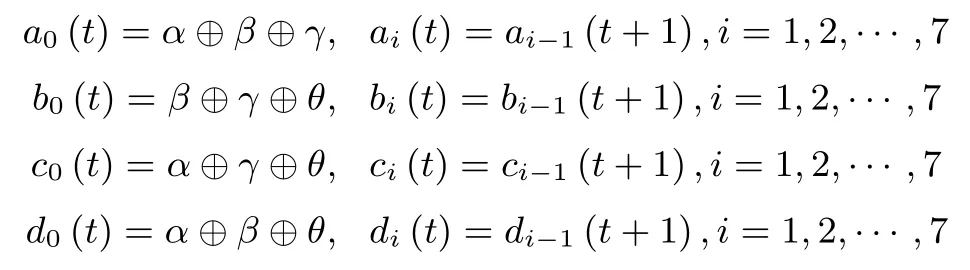
由NFSR-SR更新函数的可逆性易知下述命题2成立.

命题2基于NFSR-SR的SubRow函数是到的一一映射.

2.2.4 Transpose的定义

Transpose对内部状态矩阵进行一次转置,即

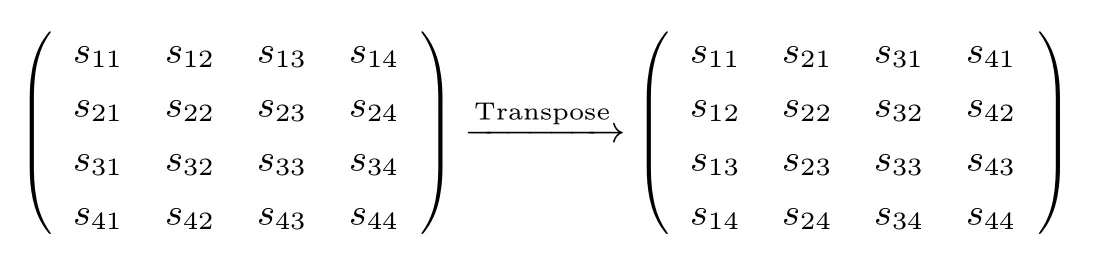
2.2.5 BitPermutation的定义

BitPermutation仅用在最后一轮轮函数FinalRound中,其功能是对内部状态的比特位置进行一次翻转.设(a7a6a5a4a3a2a1a0)是一个字节的8比特,其中a7是高位比特,记

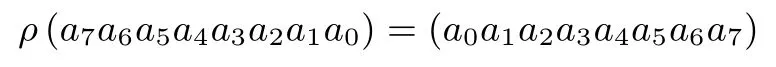
即ρ表示翻转一个字节.基于作用在字节上的ρ函数,BitPermutation的定义如下

2.2.6 KeyExpansion的设计

本小节介绍SPRING-128-128加密算法中的密钥扩展算法.设私钥为key=(k0,k1,···,k15),其中ki是一个字节,即8比特.轮子密钥由一个128比特的非线性反馈移位寄存器生成,称为NFSRKeyGeneration.该NFSR-KeyGeneration是8个16比特寄存器的环状串联结构,如图5所示,其中8个寄存器的反馈函数分别为

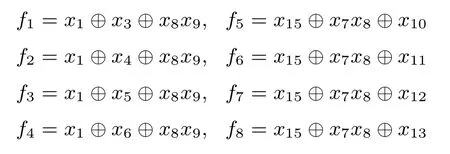
图5 非线性反馈移位寄存器NFSR-KeyGeneration示意图Figure 5 Overview of NFSR-KeyGeneration

设图5中NFSR-KeyGeneration的内部状态为其中是寄存器i的内部状态,并且具体的轮子密钥生成算法参见算法5,其中常值counter的取值参见表1.常值counter可以由一个8比特的LFSR生成,特征多项式为f(y)=y8+y4+y3+y2+1,每隔8拍取内部状态为counter值.

算法5 KeyExpansion-128-128 Inp ut:key Ou tp ut:(rk1,rk2,···,rk Nr+1)1 IS=(IS1 1,IS1 2,IS2 1,IS2 2,···,IS8 1,IS8 2)←(k0,k1,···,k15)；2 rk1←IS；3 for 2≤i≤Nr+1 d o 4 IS1 1←IS1 1⊕counter[i-1]；5 NFSR-KeyGeneration运行16拍；6 rk i←IS；7 en d

注:若记counter[i-1]=(y7,y6,···,y0),则

2.3 SPRING-128-128解密算法

SPRING-128-128解密算法与加密算法具有相似性.SPRING-128-128解密算法的轮函数InvRound-128参见算法6,最后一轮轮函数InvFinalRound-128参见算法7.

算法6 InvRound-128算法7 InvFinalRound-128 In p ut:state,RKin v i Inp ut:state,RKin v 1 AddRoundKey(state,RKi i n v)；1 AddRoundKey(state,RKi N n r v)；,RKin v N r N r+1 2 for 1≤j≤4 d o 2 for 1≤j≤4 d o 3 Inv SubRow(sj1,sj2,sj3,sj4)；4 en d 5 Transpose(state)；3 Inv SubRow(sj1,sj2,sj3,sj4)；4 en d 5 AddRoundKey(state,RKi N n r v+1)；6 BitPermutation(state)；

2.3.1 Inv SubRow与NFSR-SR-Inv的设计

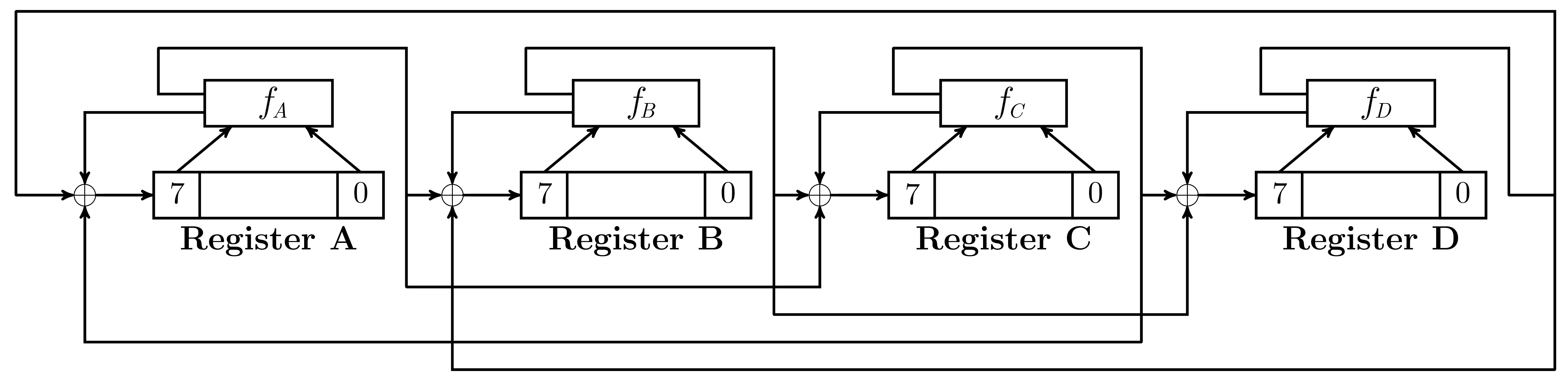
图6 非线性反馈移位寄存器NFSR-SR-Inv示意图Figure 6 Overview of NFSR-SR-Inv

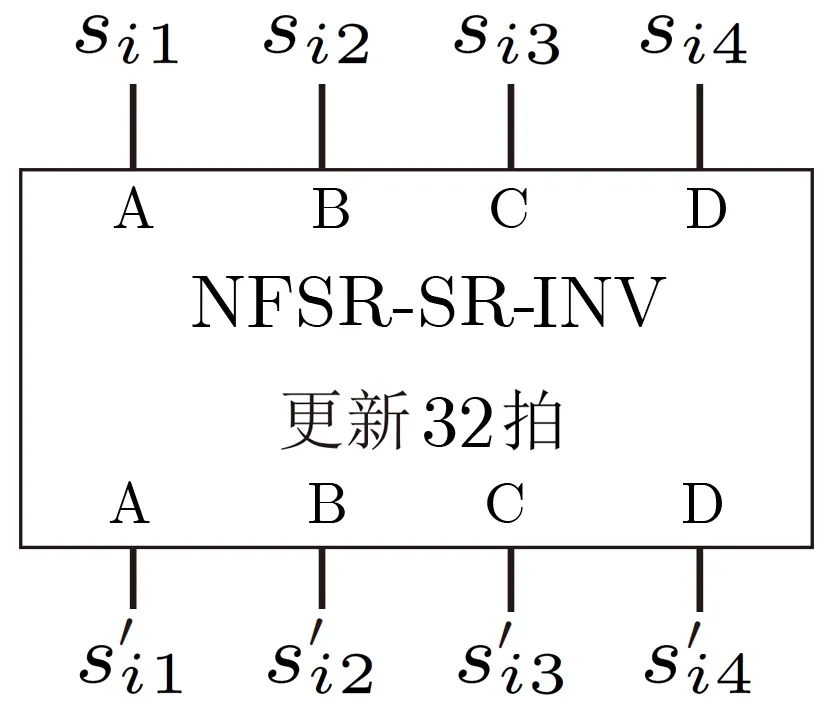
图7 NFSR-SR-Inv(si1,si2,si3,si4)示意图Figure 7 Overview of NFSR-SR-Inv(si1,si2,si3,si4)

NFSR-SR-Inv仍然是4个8比特寄存器A、B、C、D的环状串联,4个寄存器的反馈函数fA,fB,fC和fD参见第2.2.3节,也即与SubRow中4个寄存器的反馈函数是一样的.NFSR-SR-Inv的工作原理参见图6.事实上NFSR-SR-Inv与NFSR-SR可以用同一个电路来实现,仅需额外增加一个选择器,参见图8.

InvSubRow与SubRow具有以下逆映射关系.

命题3若SubRow将α=(αA,αB,αC,αD)∈映射到β=(βA,βB,βC,βD)∈,则InvSubRow将BitPermutaion(β)=(ρ(βD),ρ(βC),ρ(βB),ρ(βA))映射到BitPermutaion(α)=(ρ(αD),ρ(αC),ρ(αB),ρ(αA)),也即函数BitPermutation◦InvSubRow◦BitPermutation是SubRow的逆函数.

2.3.2 Inv KeyExpansion的设计

若在加密时,存储了所有的轮子密钥(rk1,rk2,···,rkNr+1),则在解密时对每个子密钥做一个简单的线性变换即可得到解密轮子密钥,参见算法8.

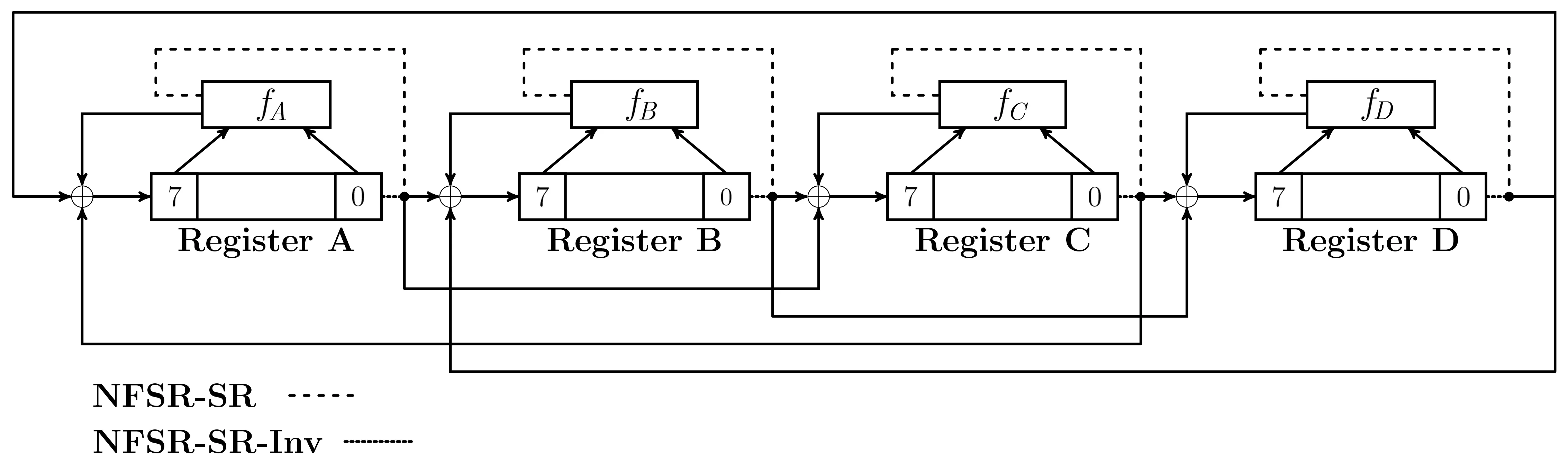
图8 NFSR-SR与NFSR-SR-Inv统一示意图Figure 8 NFSR-SR and NFSR-SR-Inv

注1为了保持解密算法与加密算法结构的一致性,我们在算法8中交换了轮密钥加和Transpose运算的顺序.

算法8 InvKeyExpansion-RK-128 Inp ut:rk1,rk2,···,rk Nr+1 Outp ut:(RKin v 1 RKinv←BitPermutation(rk N+1)；1 r1,RKi 2nv,···,RKi N n r v+1)2 for 2≤i≤Nr d o 3 RKin v←Transpose(BitPermutation(rk N-i+2))；ir 4 end 5 RKinv←BitPermutation(rk1)；Nr+1

若不存储加密算法使用的所有轮子密钥,也可以通过加密算法的最后一轮轮子密钥重新生成解密轮子密钥.设加密算法中最后一轮轮子密钥为FinalKey=(FK1,FK2,···,FK16),其中FKi是一个字节.解密轮子密钥可由一个128比特的非线性反馈移位寄存器生成,称为NFSR-KeyGeneration-Inv,如图9,其中反馈函数f1,f2,···,f8的定义参见第2.2.6节,也即与NFSR-KeyGeneration中8个寄存器的反馈函数是一样的.

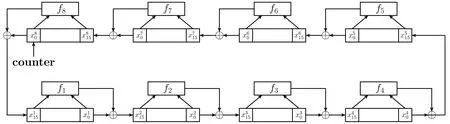
图9 非线性反馈移位寄存器NFSR-KeyGeneration-Inv示意图Figure 9 Overview of NFSR-KeyGeneration-Inv

设NFSR-KeyGeneration-Inv的内部状态为其中是寄存器i的内部状态,并且基于非线性反馈移位寄存器NFSRKeyGeneration-Inv的解密轮子密钥生成算法参见算法9.

注2比较图5与图9,易见NFSR-KeyGeneration-Inv与NFSR-KeyGeneration仅有以下两点不同:

(1)counter值加入的位置不同；

(2)反馈函数输出的拉线方向不同.

因此,在硬件设计时,可以用同一个电路实现NFSR-KeyGeneration-Inv与NFSR-KeyGeneration的功能,仅需额外增加一个线路的选择器.

算法9 InvKeyExpansion-FK-128-128 1,RKi 2n v,···,RKi N n r v+1)1 IS=(IS1 1,IS1 2,IS2 1,IS2 2,···,IS8 1,IS8 2)←(ρ(FK 16),ρ(FK 15),···,ρ(FK 1))；In p ut:FinalKey Outp ut:(RKin v 2 RKin v←IS；1 3 for 2≤i≤Nr d o 4 NFSR-KeyGeneration-Inv运行16拍；5 IS8 2←IS8 2⊕ρ(counter[Nr-i+2])；6 RKin v←Transpose(IS)；i 7 en d 8 NFSR-KeyGeneration-Inv运行16拍；9 IS8 2←IS8 2⊕ρ(counter[1])；10 k in v Nr+1←IS；

3 SPRING-128-256的设计

SPRING-128-256与SPRING-128-128的加/解密算法是一样的,不同之处仅在于轮数和密钥扩展算法.SPRING-128-256的迭代轮数为14轮.以下对SPRING-128-256的密钥扩展算法进行详细描述.

3.1 KeyExpansion的设计

设私钥为key=(k1,k2,···,k32)，其中ki是一个字节,1≤i≤32.SPRING-128-256的轮子密钥由一个256比特的非线性反馈移位寄存器生成,称为NFSR-KeyGeneration-256.该非线性反馈移位寄存器可以看成是8个32比特寄存器的环状串联结构,如图10所示,其中8个寄存器的反馈函数分别为

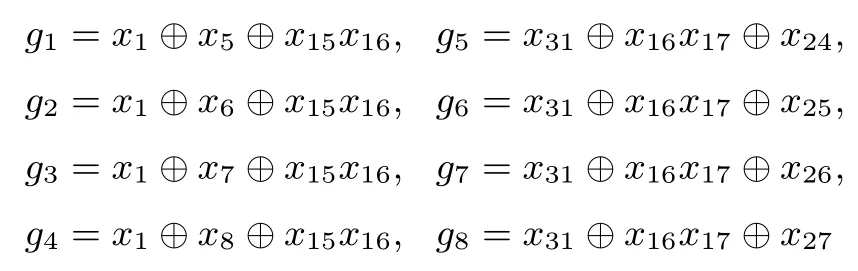
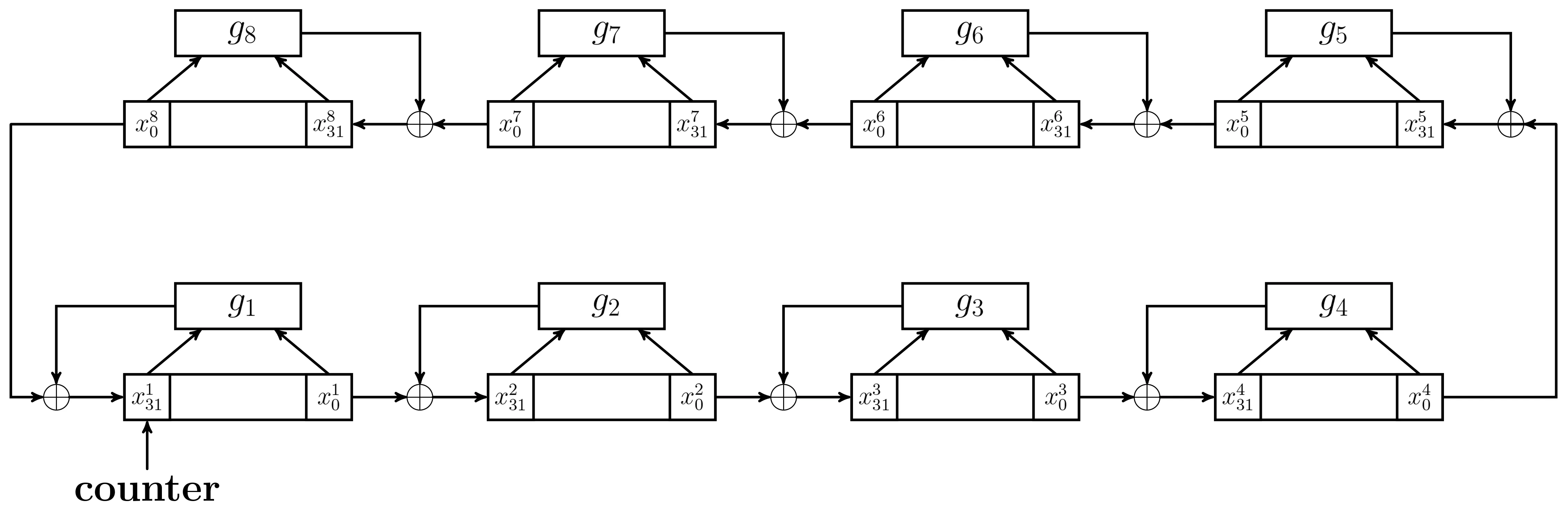
图10 非线性反馈移位寄存器NFSR-KeyGeneration-256示意图Figure 10 Overview of NFSR-KeyGeneration-256

设图10中NFSR-KeyGeneration-256的内部状态为

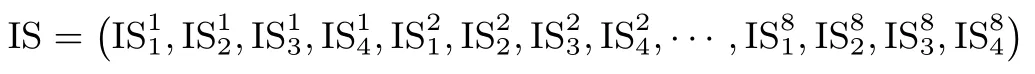
算法10 KeyExpansion-128-256 Inp ut:key Ou tp ut:(rk1,rk2,···,rk Nr+1)1 IS=(IS1 1,IS1 2,IS1 3,IS1 4,···,IS8 1,IS8 2,IS8 3,IS8 4)←(k1,k2,···,k32)；2 rk1←(IS1,IS3,IS5,IS7),其中IS i=(IS i1,IS i2,IS i3,IS i4),i=1,3,5,7；3 for 2≤i≤Nr+1 d o 4 IS1 1←IS1 1⊕counter[i-1]；5 NFSR-KeyGeneration-256运行32拍；6 rk i←(IS1,IS3,IS5,IS7)；7 en d

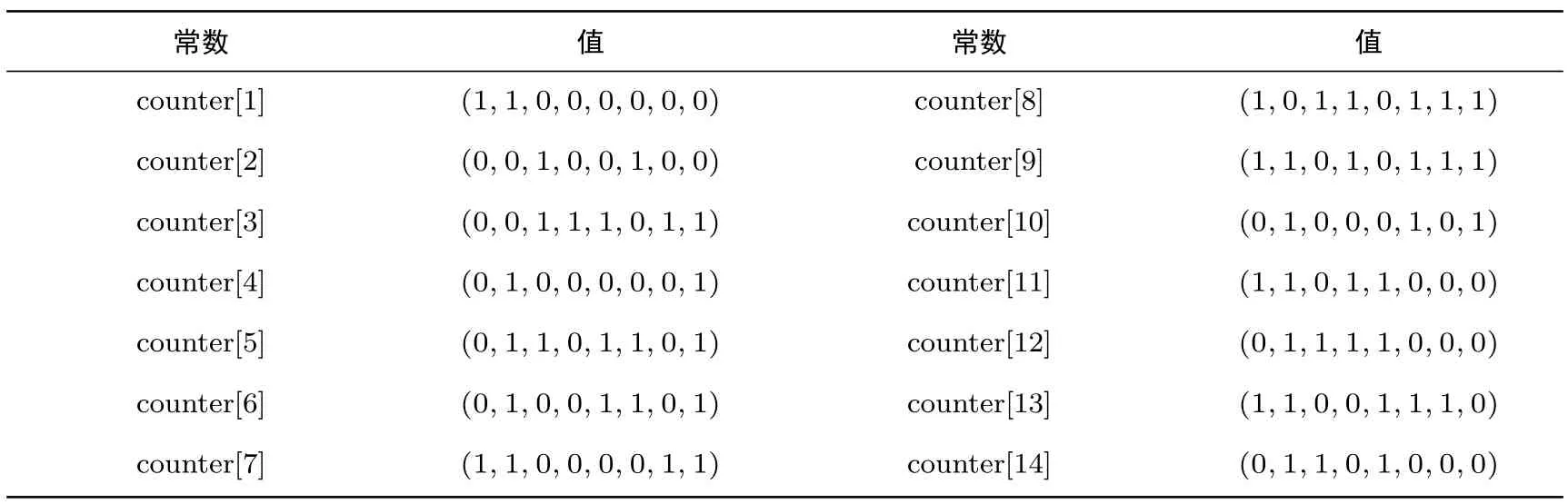
表2 SPRING-128-256密钥扩展算法中的常值Table 2 Counter values in SPRING-128-256

3.2 Inv K ey Exp ansion的设计

若在加密时,存储了所有轮子密钥(rk1,rk2,···,rkNr+1),则SPRING-128-256算法的解密密钥仅需对每个子密钥做一个简单的线性变换即可得到,即算法8,其中轮数Nr=14.

若不存储加密算法使用的所有轮子密钥,可以通过加密算法的最后一轮轮子密钥重新生成解密轮子密钥.设最后一轮轮子密钥为FinalKey=(FK1,FK2,···,FK32),其中FKi是一个字节,1≤i≤32.解密轮子密钥由一个256比特的非线性反馈移位寄存器生成,称为NFSR-KeyGeneration-Inv-256,如图11所示,其中8个寄存器的反馈函数g1,g2,···,g8与NFSR-KeyGeneration-256中是一样的.易见,NFSR-KeyGeneration-Inv-256和NFSR-KeyGeneration-256差别不大,用同一个电路实现NFSRKeyGeneration-Inv-256与NFSR-KeyGeneration-256只需要额外增加极少的硬件资源.

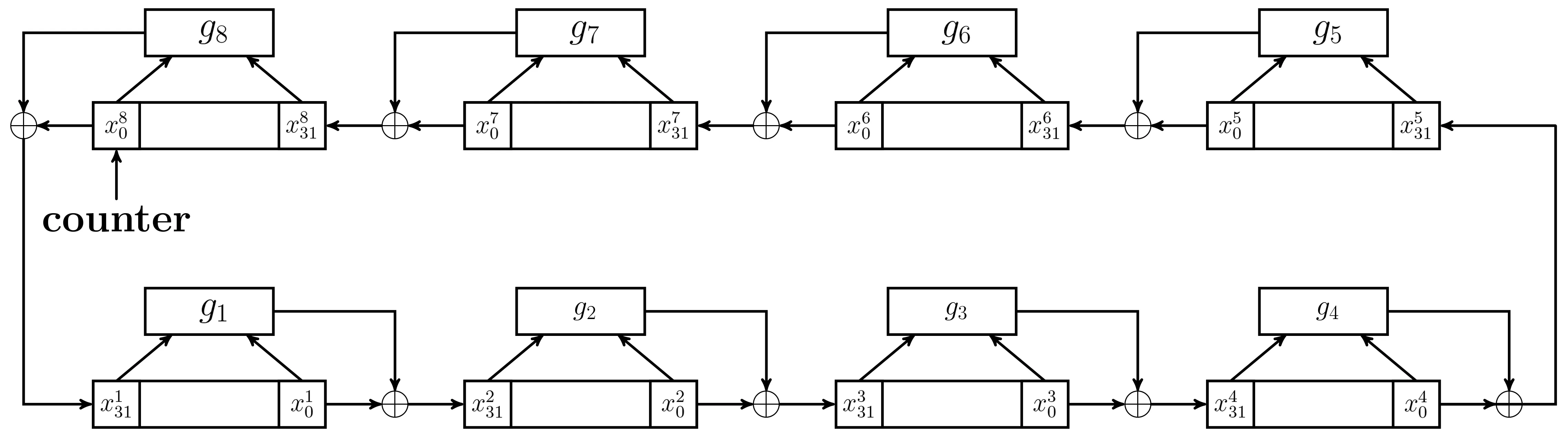
图11 非线性反馈移位寄存器NFSR-KeyGeneration-Inv-256示意图Figure 11 Overview of NFSR-KeyGeneration-Inv-256

设图11中NFSR-KeyGeneration-Inv-256的内部状态为

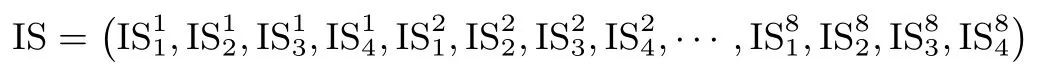
算法1 1 I n v K e y E x p a n s i o n-F K-1 2 8-2 5 6 1,r k i 2 nv,···,r k i N n r v+1)1 I S=(I S 1 1,I S 1 2,I S 1 3,I S 1 4,···,I S 8 1,I S 8 2,I S 8 3,I S 8 4)←(ρ(F K 32),ρ(F K 31),···,ρ(F K 1))；2 r k inv I n p u t:F i n a l K e y O u t p u t:(r k inv 1←(I S 2,I S 4,I S 6,I S 8),其中I S i=(I S i1,I S i2,I S i3,I S i4),i=2,4,6,8；3 f o r 2≤i≤N r d o i←T r a n s p o s e(I S 2,I S 4,I S 6,I S 8)；7 e n d 8 N F S R-K e y G e n e r a t i o n-I n v-2 5 6运行3 2拍；9 I S 8 4←I S 8 4⊕ρ(c o u n t e r[1])；4 N F S R-K e y G e n e r a t i o n-I n v-2 5 6运行3 2拍；5 I S 8 4←I S 8 4⊕ρ(c o u n t e r[N r-i+2])；6 r k inv 1 0 r k i n v Nr+1←(I S 2,I S 4,I S 6,I S 8)；

4 SPRING256-256的设计

本节介绍SPRING-256-256的设计参数.

4.1 SPRING-256-256的内部状态

SPRING-256-256的内部状态以字节为单位,看作F28上的32维向量或者F28上8×4的矩阵,即

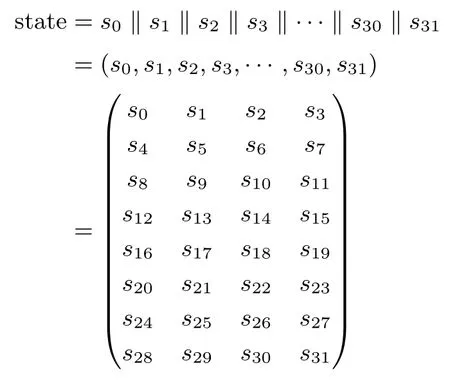
其中si为一个字节长度,即8比特,0≤i≤31.以下内部状态矩阵总是记为

设256比特的明文分组为plaintext=p0‖p1‖···‖p31,其中pi是一个字节,0≤i≤31,则用明文填充内部状态的规则为

设一个256比特密文分组为ciphertext=c0‖c1‖···‖c31,其中ci是一个字节,0≤i≤31,则内部状态与输出密文分组的对应关系为

4.2 SPRING-256-256加密算法

SPRING-256-256的加/解密结构与SPRING-128-128和SPRING-128-256是一致的.SPRING-256-256算法的迭代轮数为18轮,即Nr=18.SPRING-256-256加密算法轮函数Round-256包括三个子函数:AddRoundKey,SubRow和Transpose-256.在每一轮轮变换中,首先加轮子密钥,然后对内部状态矩阵的每一行分别做SubRow运算,最后对内部状态进行一次位置置换Transpose-256,参见算法12.

SPRING-256-256最后一轮轮函数FinalRound-256包括三个子函数:AddRoundKey,SubRow和BitPermutation,其中在SubRow运算前后各做了一次AddRoundKey,参见算法13.

算法13 FinalRound-256 Inp ut:state,rk Nr,rk Nr+1 1 AddRoundKey(state,rk Nr)；2 for 1≤j≤8 d o 3 SubRow(sj1,sj2,sj3,sj4)；4 en d 5 AddRoundKey(state,rk Nr+1)；6 BitPermutation(state)；

4.2.1 AddRoundKey定义

设AddRoundKey的输入内部状态为

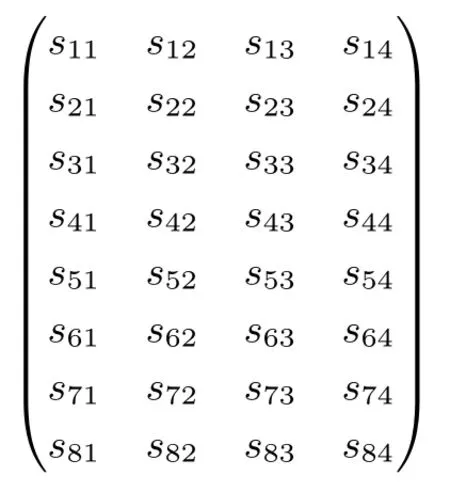
输入轮子密钥为

那么AddRoundKey的计算规则为

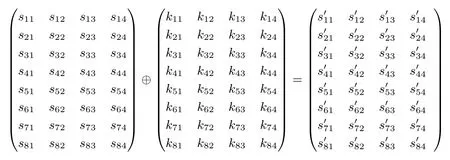
4.2.2 Transpose-256的定义

Transpose-256对内部状态矩阵进行如下置换:

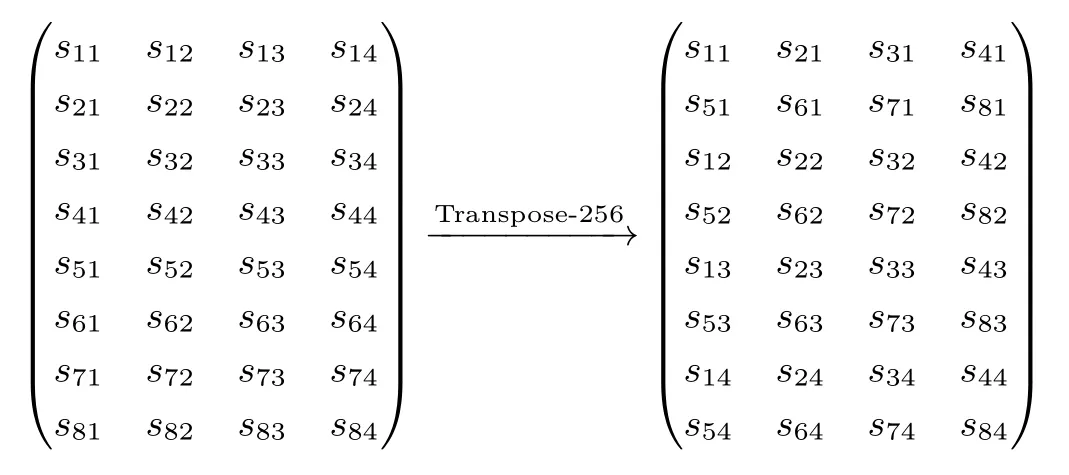
Transpose-256的逆变换记为Transpose-Inv-256,即

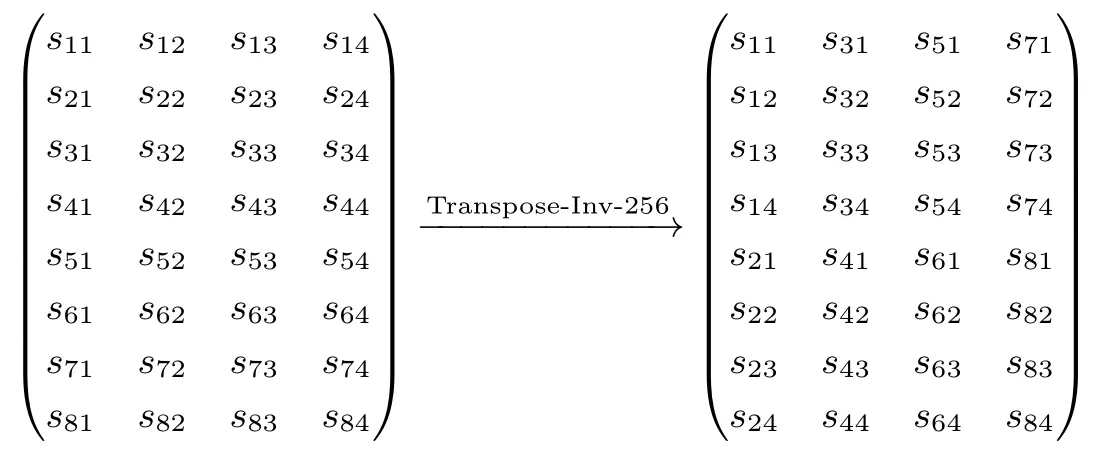
4.2.3 BitPermutation-256的定义

类似128比特分组的情形,BitPermutation仅用在最后一轮轮函数FinalRound中,其功能是对内部状态的比特位置进行一次翻转.BitPermutation的定义如下.

4.2.4 KeyExpansion的设计

设私钥为key=(k1,k2,···,k32),其中ki是一个字节,1≤i≤32.SPRING-256-256的密钥扩展算法与SPRING-128-256的基本相同,不同之处在于SPRING-128-256提取非线性反馈移位寄存器NFSR-KeyGeneration-256内部状态部分比特作为轮子密钥,而SPRING-256-256提取非线性反馈移位寄存器NFSR-KeyGeneration-256整个内部状态作为轮子密钥,具体参见算法14,其中常数counter参见表3.

算法14 KeyExpansion-256-256 Inp ut:key Ou tp ut:(rk 1,rk2,···,rk Nr+1)1 IS=(IS1 1,IS1 2,IS1 3,IS1 4,···,IS8 1,IS8 2,IS8 3,IS8 4)←(k1,k2,···,k3 2)；2 rk1←IS；3 for 2≤i≤Nr+1 d o 4 IS1 1←IS1 1⊕counter[i-1]；5 NFSR-KeyGeneration-256运行32拍；6 rk i←IS；7 end

4.3 SPRING-256-256解密算法

4.3.1 SPRING-256-256解密算法轮函数的设计

SPRING-256-256解密算法结构与加密算法是完全一致的,其中非线性变换使用Inv SubRow,线性变换使用是Transpose-Inv-256,具体描述参见算法15和算法16.需要注意的是算法15中函数Transpose-Inv-256是Transpose-256的逆变换.

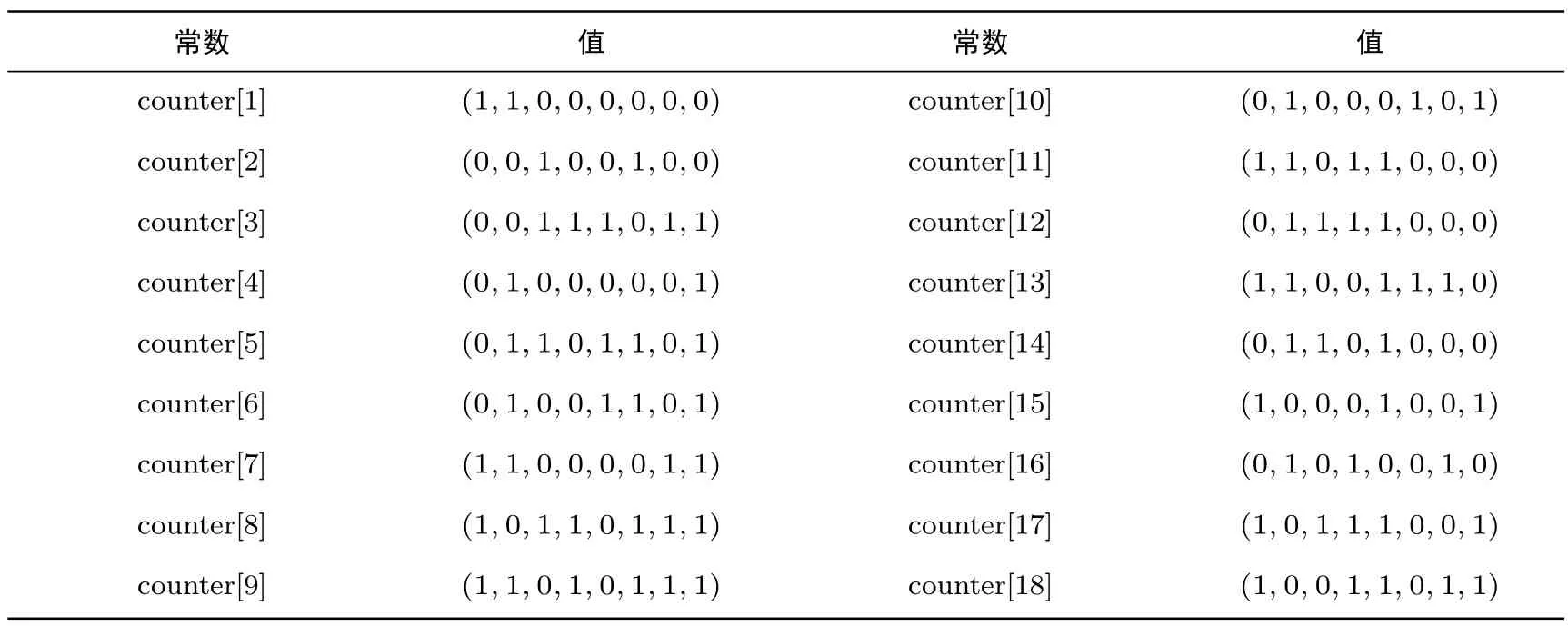
表3 SPRING-256-256密钥扩展算法中的常值Table 3 Counter values in SPRING-256-256

算法15 Inv Round-256 In p ut:state,k in v i 1 AddRoundKey(state,ki in v)；2 for 1≤j≤8 d o 3 Inv SubRow(sj1,sj2,sj3,sj4)；4 en d 5 Transpose-Inv-256(state)；

算法16 Inv FinalRound-256 In p ut:state,k in v 1 AddRoundKey(state,kN in r v)；,k in v N r N r+1 2 for 1≤j≤8 d o 3 Inv SubRow(sj1,sj2,sj3,sj4)；4 en d 5 AddRoundKey(state,kN in r v+1)；6 BitPermutation(state)；

4.3.2 Inv KeyExpansion的设计

SPRING-256-256解密算法中的密钥扩展算法与SPRING-128-256是基本相同的,不同之处仅在于轮子密钥个数不同、每次提取非线性反馈移位寄存器NFSR-KeyGeneration-Inv-256内部状态比特数量不同.

若在加密过程中,存储了所有轮子密钥(rk1,rk2,···,rkNr+1),则使用算法17来生成解密轮子密钥,其中Nr=18.

算法17 Inv KeyExpansion-RK-256 Inp ut:rk1,rk2,···,rk Nr+1 Outp ut:(RKin v 1 RKin v←BitPermutation(rk N+1)；1 r1,RKi 2n v,···,RKi N n r v+1)2 for 2≤i≤Nr d o 3 RKin v←Transpose-Inv-256(BitPermutation(rk N-i+2))；ir 4 end 5 RKin v←BitPermutation(rk1)；Nr+1

若不存储加密算法使用的所有轮子密钥,则可以通过加密算法的最后一轮轮子密钥FinalKey=(FK1,FK2,···,FK32)按照算法18重新生成解密轮子密钥,其中FKi是一个字节,1≤i≤32.

算法18 Inv KeyExpansion-FK-256-256 1,RKi 2nv,···,RKi N n r v+1)1 IS=(IS1 1,IS1 2,IS1 3,IS1 4,···,IS8 1,IS8 2,IS8 3,IS8 4)←(ρ(FK 32),ρ(FK 31),···,ρ(FK 1))；Inp ut:FinalKey Ou tp ut:(RKin v 2 RKinv←IS；1 3 for 2≤i≤Nr d o 4 NFSR-KeyGeneration-Inv-256运行32拍；5 IS8 4←IS8 4⊕ρ(counter[Nr-i+2])；6 RKin v←Transpose-Inv-256(IS)；i 7 en d 8 NFSR-KeyGeneration-Inv-256运行32拍；9 IS8 4←IS8 4⊕ρ(counter[1])；10 RKin v←IS；Nr+1

5 环状串联NFSR的性质

SPRING算法中实现S-盒功能的NFSR-SR和实现密钥扩展功能的NFSR-KeyGeneration均是环状串联非线性反馈移位寄存器.环状串联非线性反馈移位寄存器的概念最早在文献[2]中提出,文中证明了环状串联非线性反馈移位寄存器中每个寄存器的输出序列具有相同的周期性质.NFSR-KeyGeneration是典型的环状串联结构,完全符合文献[2]的研究模型.NFSR-SR是一个扩展的环状串联结构,为了扩散更快,在原文献[2]的研究模型基础上,增加了四根对称的拉线,依然具有类似环状串联的对称结构.

对于环状串联结构的NFSR,我们认为经过充分多的内部状态更新后,每个比特寄存器具有非常等价的地位,从而输出比特关于输入比特具有相似的密码学性质,并且整体性强,输入输出不容易分割成独立的小单元.

6 SubRow运算的基本性质

在本节中,我们对SPRING算法中唯一的非线性运算SubRow进行了分析和测试.SubRow是F322到的函数,实际由32比特的非线性反馈移位寄存器NFSR-SR实现.

6.1 代数性质

我们计算了SubRow运算每一个输出比特分位函数的真值表,通过Meobius变换[3]分别计算出了32个输出比特分位函数的代数正规型.表4给出了每一个分位函数的代数次数和项数.观察表4可以发现,各个输出比特分位函数的代数次数比较高并且项数稠密.

6.2 扩散性质

我们对非线性反馈移位寄存器NFSR-SR的扩散性质进行了测试.实验结果显示,经过25轮迭代后,NFSR-SR内部状态的每一比特与输入的每一比特相关,也即每一状态比特函数的代数正规型包含32个输入比特变元.注意到在SubRow函数中NFSR-SR迭代32拍,因此SubRow函数的每一输出比特与32个输入比特变量相关.

6.3 差分性质

注意到SubRow运算是一个32比特的非线性置换,计算和存储整个差分分布表远远超出了普通计算机的计算能力.因此,我们对SubRow运算的差分性质进行了以下测试.

首先,我们利用太湖之光超级计算机穷尽了SubRow运算的差分分布表,得到SubRow运算的最大差分概率等于即

并且有且仅有一对差分(α,β)取到上述最大值,即

其中从高位到低位依次为寄存器

的差分.

其次,对于NFSR的迭代模型,相对于多重的输入差分,一般单重输入差分扩更散慢.例如在Grain v1的条件差分攻击中[4,5],输入差分是单重差分.于是,我们计算了所有的单重输入差分对应的输出差分分布表.表5给出了全体单重输入差分可以取到的最大差分概率.

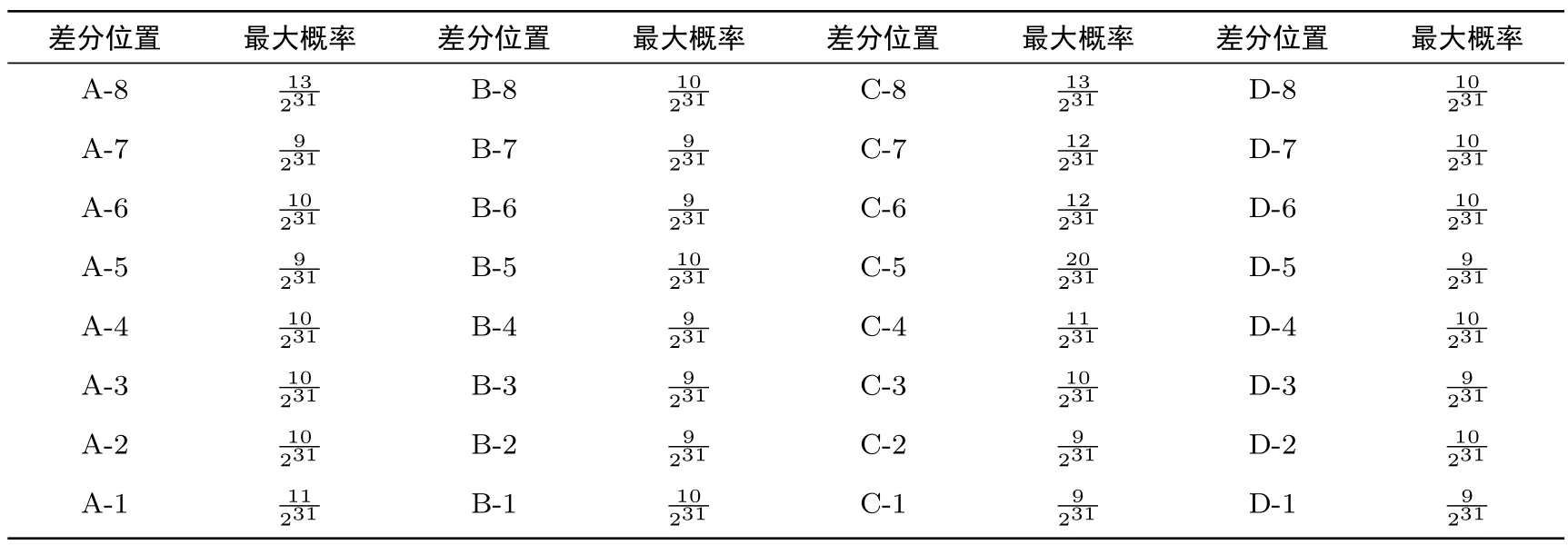
表5 单重输入差分的最大差分概率Table 5 Maximal difference probability for input differences with one nonzero bit

最后,因为SPRING算法的线性扩散层是字节拉线,所以我们对单字节到单字节的差分概率进行了检测,记录了各输入字节到各输出字节的最大差分概率,见表6.

表6 输入字节到输出字节最大差分概率Table 6 Maximal difference probability for byte-based differences

7 硬件性能分析

SPRING系列算法主要是面向硬件实现设计的.根据不同的需求,可以调节实现面积与加解密速率.按轮实现,面积最小；全轮展开实现,加解密速率最大.我们用Design Complier对SPRING-128-128、SPRING-128-256、SPRING-256-256的两种实现方式进行了综合,其中工艺库为TSMC 16 nm,具体结果见表7和表8.

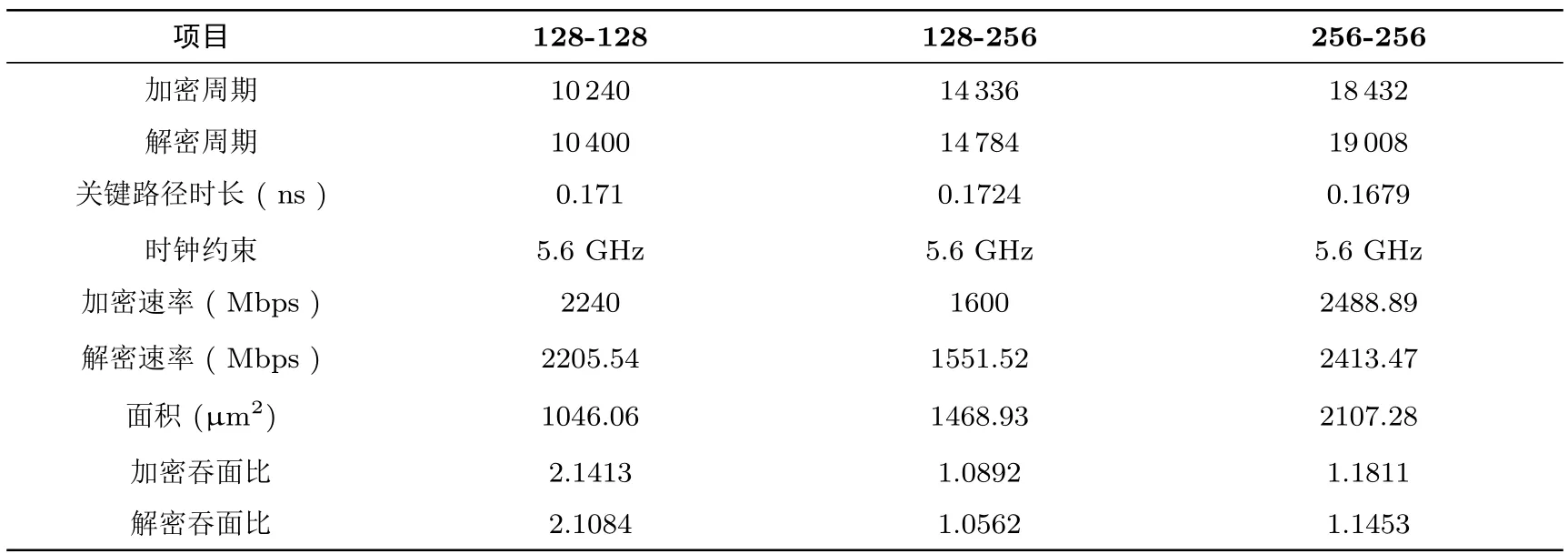
表7 单轮实现方式下SPRING算法的检测数据Table 7 Test data for SPRING under round-based implementation

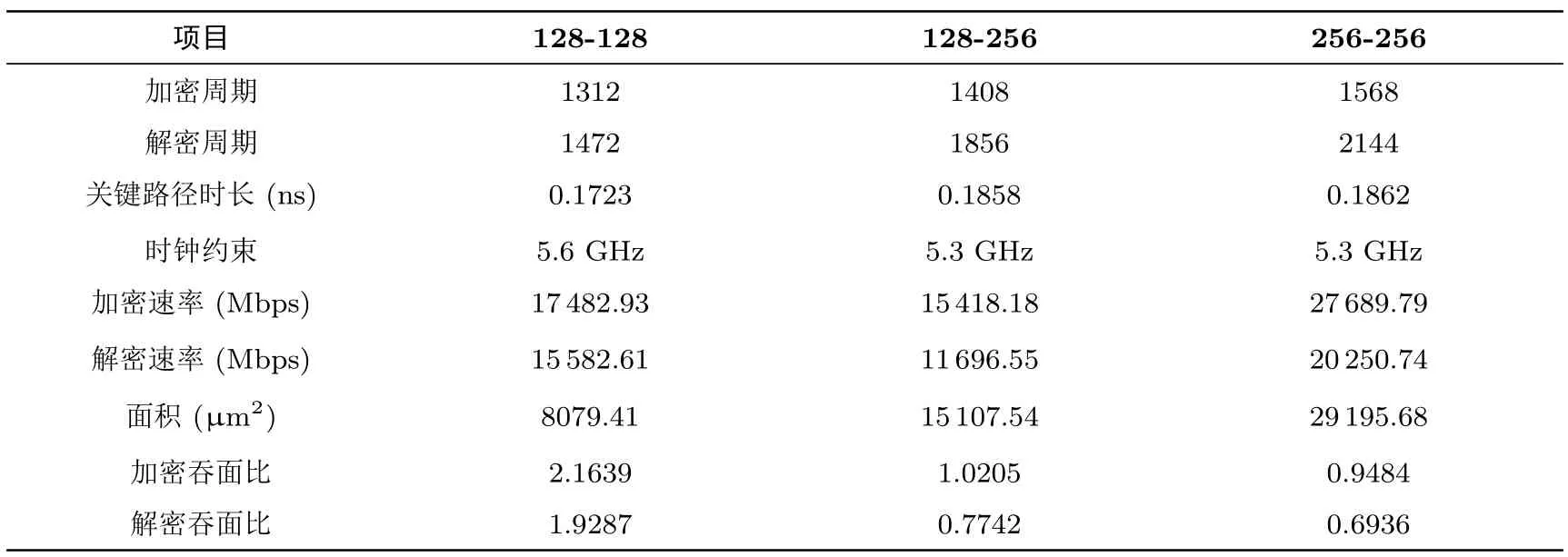
表8 全轮实现方式下SPRING算法的检测数据Table 8 Test data for SPRING under unrolled implementation

8 总结

SPRING是基于非线性反馈移位寄存器设计的轻量级分组密码.SPRING采用SP结构,非线性替换层通过32比特非线性反馈移位寄存器实现,置换层是字节拉线,加/解密对称,整体结构简洁.用于SPRING替换层的32比特非线性反馈移位寄存器可以看作32进32出的可逆S-盒,而普通计算机无法穷尽其差分分布表和线性逼近概率表,这使得传统的差分和线性分析方法很难应用到SPRING算法.目前,SPRING算法最有效的差分分析方法是面向单字节的分析,存在4轮单字节到单字节的有效差分特征.