NBC算法*

徐洪,段明,谭林,戚文峰,王中孝

信息工程大学,郑州450001

1 引言

NBC算法是我们团队设计的一种分组密码算法,支持128/128比特、128/256比特和256/256比特三种分组和密钥长度,能够满足未来应用环境下的安全需求.

本文将详细介绍NBC算法,第2节给出NBC算法的完整描述,介绍算法的轮函数、S盒和密钥扩展算法,第3节简要介绍算法的设计原理,第4节是算法的安全性分析,最后是简单的小结.

2 算法描述

本节给出NBC算法的完整描述.下面要用到的基本符号如下:

⊕:逐比特异或

⊗:逐比特与

+:模2n加法

Xi:第i轮的输入

Ki:第i轮的轮子密钥

NBC算法采用改进的第二类广义Feistel结构,轮函数如图1和图2所示,其中S为16比特的S盒,π为16比特块的置换.

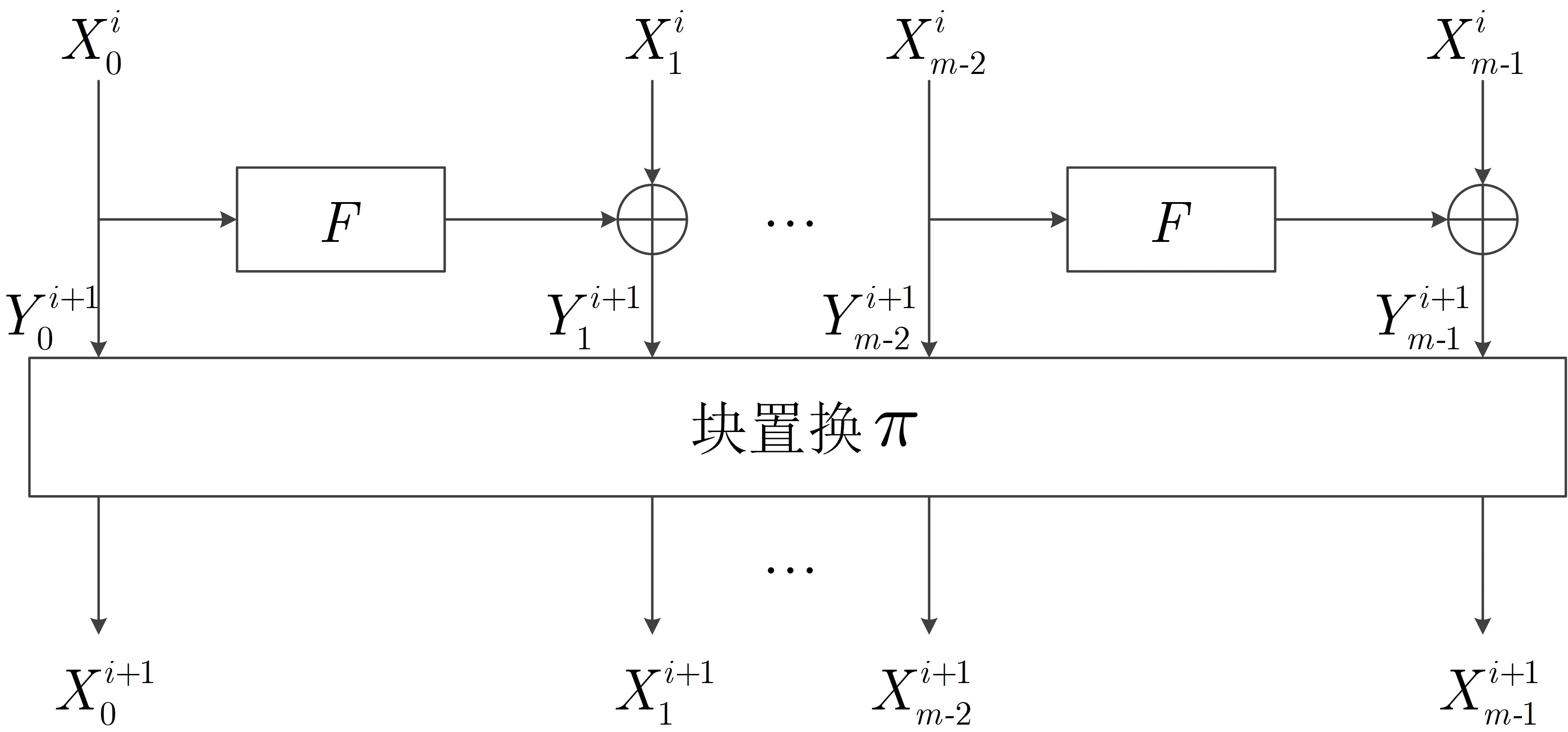
图1 NBC算法的轮函数Figure 1 Round function of NBC algorithm

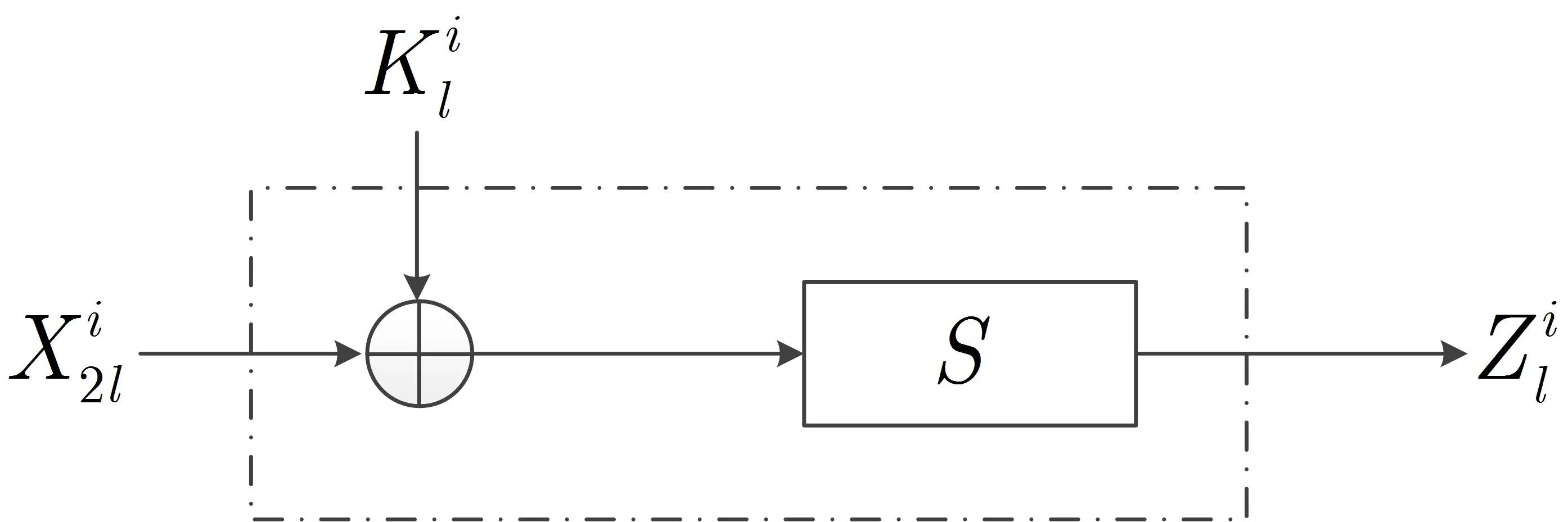
图2 F函数(0≤l≤m/2-1)Figure 2 F function(0≤l≤m/2-1)

算法以16比特为基本处理单元,以下将分组长度为16m比特,密钥长度为16n比特的NBC算法简记为NBC 16m/16n算法.算法支持128/128、128/256、256/256等三种分组和密钥规模,迭代轮数分别为32、34、38,基本参数见表1.当不强调密钥长度时,也简单记NBC 128为分组长度为128比特的NBC算法,NBC 256为分组长度为256比特的NBC算法.

表1 NBC算法基本参数Table 1 Parameters for NBC algorithm

2.1 轮函数

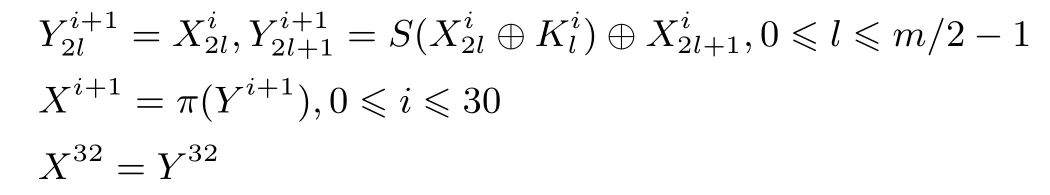
为保证加解密的一致性,最后一轮不进行块置换.输入明文为P=X0,输出密文为C=X32.

对于128和256比特分组,相应的块置换π分别为

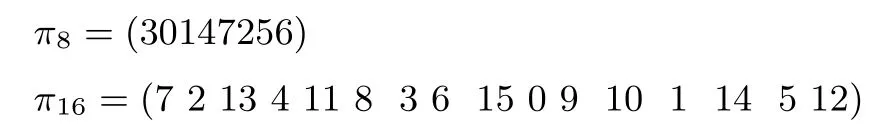
其中(30147256)中的3表示输入的第0块移到输出的第3块的位置,其余依此类推.图3和图4分别为128和256比特分组的NBC算法的轮函数示意图.

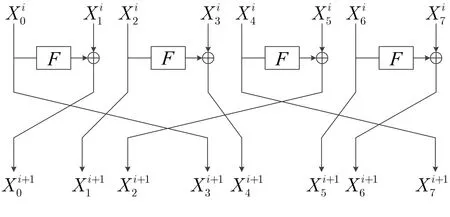
图3 NBC 128算法的轮函数Figure 3 Round function of NBC 128 algorithm

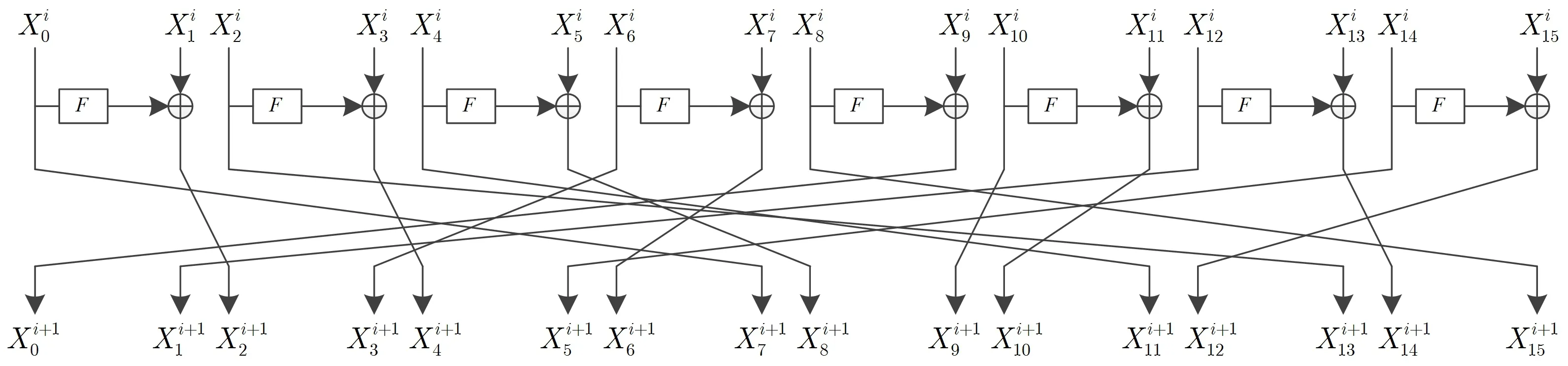
图4 NBC 256算法的轮函数Figure 4 Round function of NBC 256 algorithm

2.2 S盒

NBC算法的S盒基于16级的非线性反馈移位寄存器(NFSR)来构造,参见图5.设S盒的16比特输入为s0,s1,···,s15,将该16比特从左至右依次填充至16个寄存器内,寄存器迭代20拍后的全体内部状态即为S盒的输出.

寄存器每迭代一拍,除常规移位外以非线性方式同时更新4个比特,设某时刻寄存器的输入为s0,s1,···,s15,输出为则其状态更新函数如下

图5 用于构造S盒的非线性反馈移位寄存器Figure 5 NFSR for constucting S-box

寄存器迭代20拍可以保证S盒的各分量的代数次数都达到最大值15,并且具有好的差分和线性性质.

2.3 密钥扩展算法

密钥扩展算法的设计与S盒类似,采用基于n比特字的16级非线性反馈移位寄存器,其中128比特密钥对应的n=8,256比特密钥对应的n=16.密钥扩展算法中引入模2n加法代替比特与,增加了循环移位以保证不同字之间的充分混淆,增加了轮常数以避免出现弱密钥(如全零子密钥).密钥扩展算法中用到的非线性反馈移位寄存器的示意图如图6所示,图中的状态字wj(0≤j≤15)和常数cl(0≤l≤3)中各比特都是按照高位在前,低位在后的顺序存放.

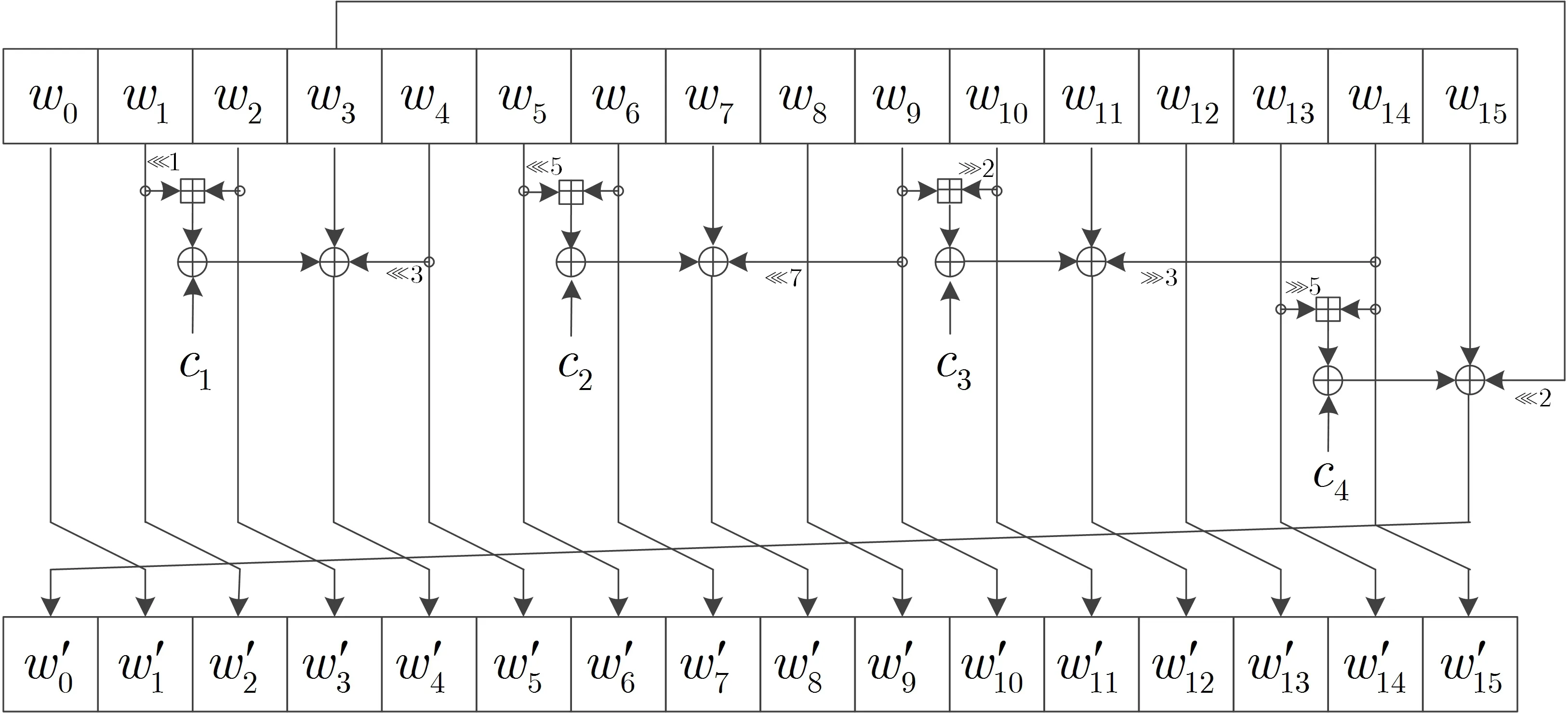
图6 密钥扩展算法中用到的非线性反馈移位寄存器Figure 6 NFSR used in KeyGeneration algorithm

初始种子密钥为16n比特,分成16个n比特字K=(k0||k1||···||k15).用它们填充密钥寄存器的初态,即有wj=kj,0≤j≤15.提取密钥寄存器的前8m比特作为初始轮的轮子密钥.之后寄存器每迭代4拍,输出一轮轮子密钥,每次选取密钥寄存器的前8m比特作为轮子密钥.要产生r轮加密的所有轮子密钥,密钥寄存器总共需要迭代4(r-1)拍.轮子密钥的具体产生方式如下

(1)对0≤j≤15,令wj=kj；

(2)输出密钥寄存器的前8m比特作为第0轮的轮子密钥K0；

(3)对1≤i≤r-1,顺序执行下列步骤,产生后r-1轮的轮子密钥Ki；

(a)寄存器迭代4拍,按下列方式更新寄存器状态:

(b)选取密钥寄存器的前8m比特作为第i轮的轮子密钥Ki.三种情况下输出的轮子密钥分别为:

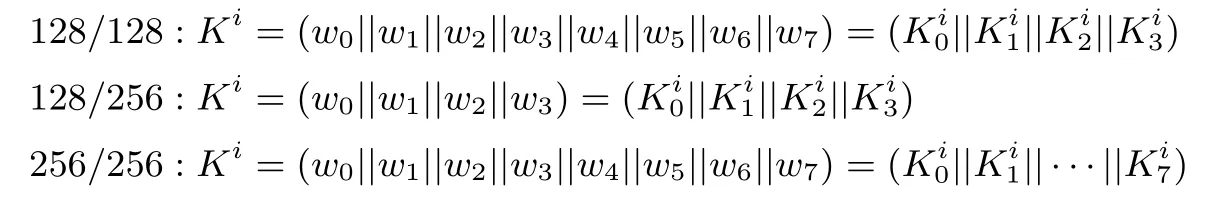
密钥扩展算法中用到的轮常数cl=rl⊕i(0≤l≤3),其中rl为随机数,256比特密钥时用到的4个16比特随机数分别为:

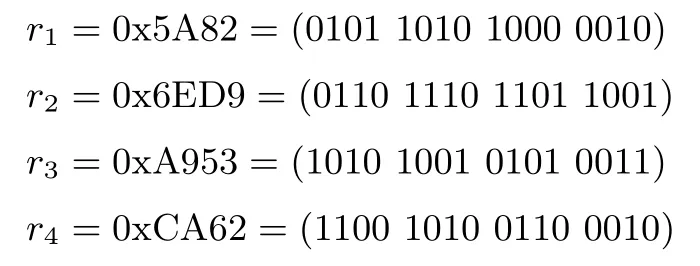
3 设计原理

3.1 轮函数的设计

轮函数采用Suzaki等[1]在FSE 2010会议上给出的改进型的第二类广义Feistel结构,扩散层选用了新的块置换,该结构比扩散层采用循环移位的第二类广义Feistel结构扩散效果更好.比如,m分支的第二类广义Feistel结构需要m轮才能完全扩散,而采用这种改进版的结构,最优情况下8分支仅需要6轮,16分支仅需要8轮就可以完全扩散.兼顾最小活动S盒个数达到最优,对于8分支和16分支的广义Feistel结构,我们分别采用了Suzaki等给出的第1个和第10个最优扩散层实例.它们不同轮数对应的最小活动S盒个数如表2、表3.

当S盒的差分和线性性质较好时,经过适当轮迭代后可以保证算法具有足够的抵抗差分和线性分析的能力.

表2 不同轮数最小活动S盒个数(NBC 128算法,8分支GFS)Table 2 Minimum active S-box under different round(NBC 128 algorithm,8 branch GFS)

表3 不同轮数最小活动S盒个数(NBC 256算法,16分支GFS)Table 3 Minimum active S-box under different round(NBC 256 algorithm,16 branch GFS)

3.2 S盒设计

在S盒的构造上,我们采用了Galois结构的16级非线性移位寄存器(NFSR)来构造轻量化的16比特S盒,除常规移位外每次以非线性方式更新4个比特.硬件实现时仅需要3个与门,1个与非门和8个异或,约需要3×1.25+1×1+8×2=20.75个标准门电路.

迭代20拍后,寄存器各个比特关于初始状态的代数次数都可以达到15次.构造出的S盒的差分均匀度为Diff(S)=22,最大差分概率为22/216≈2-11.541,线性度为Lin(S)=1572,最大线性概率为1572/216≈2-5.382.这里的差分均匀度和线性度分别为:

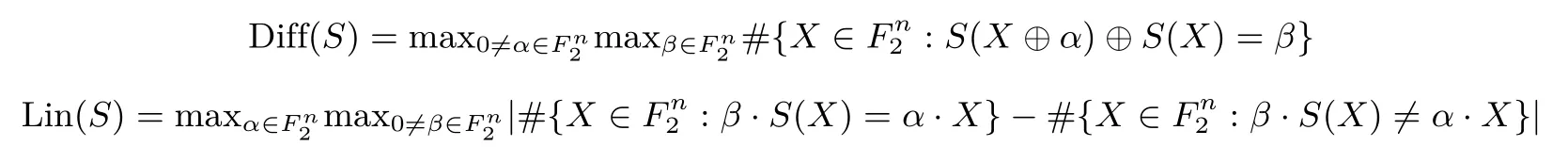
3.3 密钥扩展算法的设计

密钥扩展算法采用了与S盒构造类似的基于n比特字的16级非线性反馈移位寄存器结构,128比特和256比特密钥情况下,字长分别为8比特和16比特.寄存器非线性部分的比特与运算改成模2n加法运算,同时引入循环移位使得寄存器各个字之间可以更快扩散.寄存器中引入轮常数以抵抗滑动攻击,并避免出现弱密钥.由于密钥寄存器每迭代4拍才输出一轮轮子密钥,每次只输出密钥寄存器的前一半或者四分之一比特.因此,同一轮子密钥的不同块之间、前后轮轮子密钥的不同块之间不存在简单的依赖关系,这也增加了密钥恢复过程的复杂度.由于密钥寄存器按非线性方式迭代更新,仅知道部分子密钥块仍然难以有效恢复全部主密钥.

4 安全性分析

目前的研究表明NBC算法能够抵抗差分、线性、不可能差分、零相关线性、积分分析等主要密码分析方法,具有较多的安全冗余.

4.1 差分分析和线性分析

对于差分和线性分析,利用前面得到的活动S盒个数以及S盒的最大差分和线性概率可以给出相应的差分和线性安全界.

已知单个S盒的最大差分概率约为2-11.541,最大线性概率约为2-5.382.对于NBC 128算法,由3.1节的表2知,9轮迭代后至少有12个差分和线性活动S盒,相应的最大差分概率

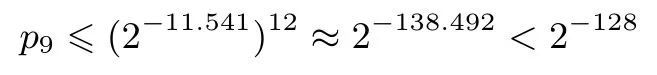
最大线性概率为

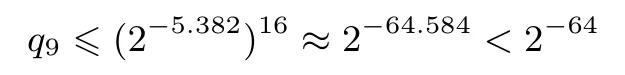
故NBC 128算法经过9轮迭代后可以抵抗基本差分分析和线性分析,而NBC 128/128和NBC 128/256算法总的迭代轮数分别为32和34轮,有足够的安全冗余.

类似的,由表3知,NBC 256算法经12轮迭代后至少有24个差分和线性活动S盒,相应的12轮最大差分概率为

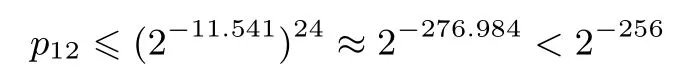
最大线性概率为

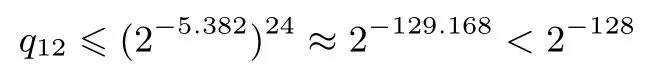
故NBC 256算法经过12轮迭代后可以抵抗基本差分分析和线性分析,而NBC 256/256算法总迭代轮数为38轮,也有足够的安全冗余.

4.2 不可能差分分析

对于分组长度为128比特的NBC 128算法,利用中间相错方法容易验证当a/=b时,该算法存在形如(0a000000)↛11(0000b000)的11轮不可能差分特征.按照Boura等[2]在2014年亚密会上提出的不可能差分分析的一般理论模型,在该不可能差分特征前后各添加3轮可以给出NBC 128/128算法的17轮不可能差分分析,在该不可能差分特征前后各添加4轮可以给出NBC 128/256算法的19轮不可能差分分析.

对于分组长度为256比特的NBC 256算法,利用中间相错方法容易验证NBC 256算法存在形如(0α10α30α50α70α90α110α130α15)↛14(β00β20β40β60β80β100β120β140)的14轮不可能差分特征,其中αi,βj仅一个非零.在该不可能差分特征前后各添加4轮可以给出NBC 256/256算法的22轮不可能差分分析.

4.3 零相关线性分析

对于分组长度为128比特的NBC 128算法,利用中间相错方法容易验证当a/=b时,该算法存在形如(a0000000)→11(0000000b)的11轮零相关线性特征.按照Bogdanov,Wang等[3,4]给出的多维零相关线性分析的方法,在该零相关线性特征前后各添加2轮可以给出NBC 128/128算法的15轮零相关线性分析,在该零相关线性特征前面添加2轮后面添加3轮可以给出NBC 128/256算法的16轮零相关线性分析.

对于分组长度为256比特的NBC 256算法,利用中间相错方法容易验证NBC 256算法存在形如(α00α20α40α60α80α100α120α140)→14(0β10β30β50β70β90β110β130β15)的14轮零相关线性特征,其中αi,αj仅一个非零.在该零相关线性特征前后各添加3轮可以给出NBC 256/256算法的20轮零相关线性分析.

4.4 积分分析

对于分组长度为128比特的NBC 128算法,利用基于可分性质的积分特征搜索方法[5,6],可以找到NBC 128算法的形如

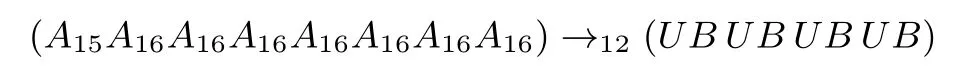
的12轮积分特征.由于NBC算法使用了16比特的S盒,暂时没法利用基于比特的可分性质[7-9]找到更好的积分特征.利用中间相遇和部分和技术,在该积分特征后面添加4轮可以给出NBC 128/128算法的16轮积分攻击,添加6轮可以给出NBC 128/256算法的18轮积分攻击.

对于分组长度为256比特的NBC 256算法,类似可以找到NBC 256算法的形如(A15A16A16···A16)→12(UB···UB)的16轮积分特征,在该积分特征后面添加6轮可以给出NBC 256/256算法的22轮积分攻击.

综合上面的分析,对于NBC 128/128算法,9轮迭代后可以抵抗基本差分分析和线性分析,至多存在17轮不可能差分攻击,15轮零相关线性攻击和16轮积分攻击,算法的迭代轮数为32轮,有足够的安全冗余.对于NBC 128/256算法,9轮迭代后可以抵抗基本差分分析和线性分析,至多存在19轮不可能差分攻击,16轮零相关线性攻击和18轮积分攻击,算法的迭代轮数为34轮,有足够的安全冗余.对于NBC256/256算法,12轮迭代后可以抵抗基本差分分析和线性分析,至多存在22轮不可能差分攻击,20轮零相关线性攻击和22轮积分攻击,算法的迭代轮数为38轮,也有足够的安全冗余.

5 结束语

NBC系列算法是我们团队为分组密码算法设计竞赛提交的分组算法.算法整体采用改进的第二类广义Feistel结构,结构非常简单,便于软硬件实现和安全性分析,轮函数和S盒都采用了轻量化的设计.算法的扩散层采用基于块的置换,S盒采用了16比特的大S盒,基于16级非线性反馈移位寄存器构造,构造S盒时只用到了3个与、1个与非和8个异或,具有非常低的硬件实现成本.算法能够抵抗差分、线性、不可能差分、积分等主要密码分析方法,有较充足的安全冗余.