ANT系列分组密码算法*

陈师尧,樊燕红,付勇,黄鲁宁,王美琴

1.山东大学网络空间安全学院,青岛266237

2.密码技术和信息安全教育部重点实验室,青岛266237

1 引言

1.1 背景

近年来,随着日常生活中物联网设备越来越多,这些资源受限设备下的数据传输安全也越来越受到人们的重视.传统的分组密码如AES[1]等并不适合一些资源受限的环境.因此,轻量级的分组密码成为了当前的一个研究热点.密码学界也设计了许多轻量级的分组密码,如LED[2]、LBlock[3]、Rectangle[4]、PRINCE[5]和Zorro[6]等.其中,一些高效的轻量级算法已经成为了ISO/IEC标准,如PRESENT[7]和CLEFIA[8].伴随着5G技术的广泛应用,物联网所承载的通讯设备的数量必然会与日俱增.因此,为了更好地适应物联网设备多样化以及轻量化的趋势,NIST[9]在征集新的标准密码算法时也自然会考虑到这些应用场景和需求.

然而,学界并未对轻量级给出严格的定义,不同的受限应用环境也有不同的需求.比如,面积小(尺寸受限的芯片设备)、功率低(被动式RFID)、能耗少(电池供能的设备)以及延时低(磁盘加密).因此,人们通常关注的指标有功率、能耗、硬件面积和吞吐量.但当把这些指标都纳入考虑范围,不同轻量级算法之间的比较自然是一项非常复杂的工作.通常来说,硬件面积是大家公认的一个主要性能指标.近年来,人们也提出了一个更全面的指标—吞面比,来衡量一个密码算法硬件实现过程中性能与资源消耗折衷的能力.在一定程度上,一个密码算法功率和能耗的高低也可以通过其吞面比反映出来.正是在这些指标需求的推动下,近年来涌现出许多优秀的轻量级密码算法,其中大部分都是SPN结构的算法,如SKINNY[10]和GIFT[11]等.与之相比,Feistel结构的算法由于扩散性较慢,并未受到轻量级设计的青睐.但Feistel结构具有天然的加解密一致的优势,这对硬件实现非常有利.因此,如何达到更快的扩散速度,对基于Feistel结构的轻量级分组密码设计至关重要,也决定着其是否能发挥出优异的硬件性能.

结合这样的背景和需求,我们致力于设计一款适合轻量级实现,同时具有较好软件性能且安全强度高的分组密码算法.

1.2 主要贡献

本文给出了一个主要面向硬件实现兼具出色多路软件性能的分组密码算法—ANT,其包含三个版本:ANT-128/128、ANT-128/256和ANT-256/256.其主要特点如下:

·实现效率高.ANT算法采用经典的Feistel结构,具有加解密一致的优势.而精心构造的基于比特级的轮函数,仅采用了与操作、循环移位操作和异或操作(AND-Rotation-XOR).这些设计理念的结合,使ANT算法的硬件实现性能优异,所有版本均具有较小的面积和较高的吞面比.其中,ANT-128/128在硬件实现平台(HJTC 110 nm标准元件库)下,加解密基于轮的实现仅需硬件面积3220 GE.软件方面,在设计过程中充分考虑了bitslice的实现性能,因此ANT算法具有出色的多路软件实现速率.

·安全强度高.我们基于可满足性问题(Boolean satisfi ability problem,SAT)的自动化搜索方法[12]对现有常见的攻击方法进行了分析.分析结果表明ANT算法能够抵抗现有攻击方法,各版本具有充分的安全冗余.

·侧信道防护代价小.目前的侧信道攻击大多针对算法中的S盒进行.ANT算法采用AND操作作为唯一的非线性操作,同传统的S盒算法相比,其针对侧信道攻击的防护更容易实现且代价更小.

1.3 本文框架

本文章节内容安排如下:第2节给出ANT的算法描述,第3节介绍ANT的算法设计原理,第4节和第5节分别给出ANT算法的安全性分析和软硬件实现结果.最后,第6节总结全文.

2 ANT算法描述

本节将给出ANT系列分组密码算法的详细说明.ANT系列分组密码算法采用了经典的Feistel结构,其所有分组可用ANT-2n/m表示.不同分组的相应参数在表1中具体给出.

表1 ANT系列分组密码算法相应参数Table 1 Parameters for ANT family block cipher

本文中采用的一些符号表示如下:

·x=xn-1‖xn-2‖···‖x0:n比特变量x(从高位到低位).

·x≪a:变量x左移位a比特.

·x⋘b:变量x左循环移位b比特.

·x⊕y:变量x和变量y进行异或操作.

·x⊙y:变量x和变量y进行与操作.

2.1 轮函数

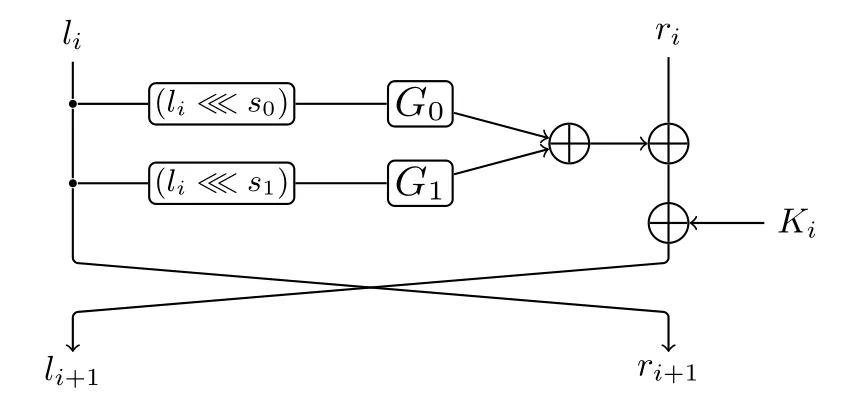
图1 ANT算法轮函数Figure 1 Round function of ANT

ANT算法的轮函数仅采用AND,Rotation,XOR三种操作,结构如图1所示,可以由如下公式表示:

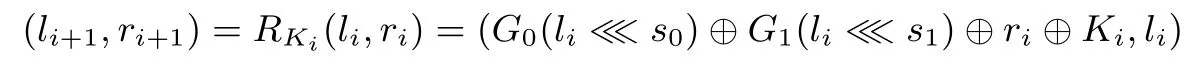
其中,轮数变量i有0≤i＜R.注意为保证加解密一致,最后一轮的左右支经过轮函数之后不进行交换.循环移位参数(s0,s1)在ANT所有的分组中均设置为(3,16).G0和G1为比特级的非线性函数,包含2层,2层之间是一层比特级的置换.在具体介绍G0和G1之前,先引入如下表示:

对于G0:

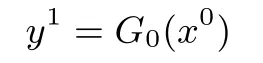
先经过G0中的第一层

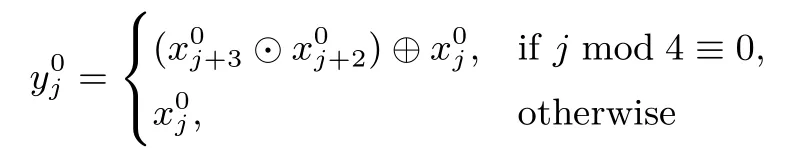
再经过中间的置换PERM

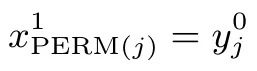
最后经过第二层

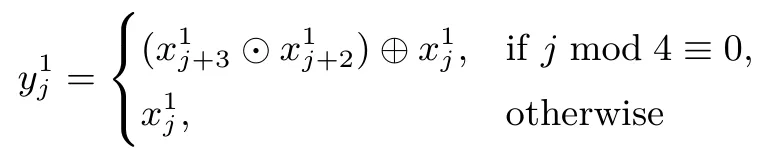
类似的,对于G1:

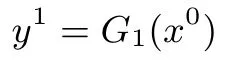
先经过G1中的第一层

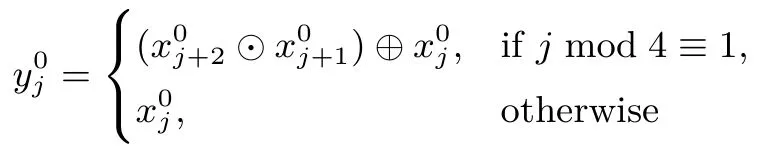
再经过中间的置换PERM

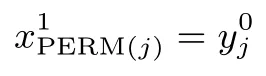
最后经过第二层

对于不同ANT分组中所采用的置换PERM,其表达式如下(PERM置换的表格形式见表2和表3),

对于ANT-128:

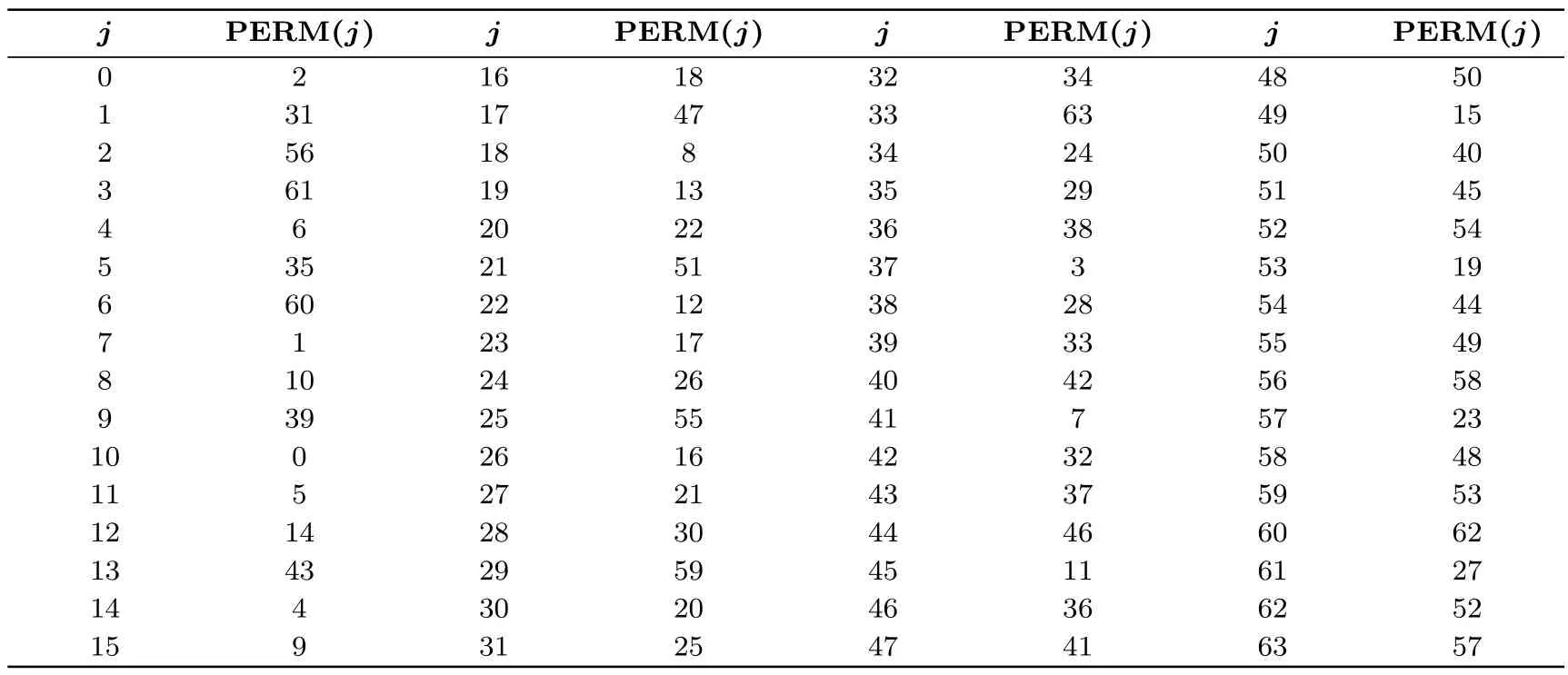
表2 ANT-128的PERMTable 2 PERM in ANT-128

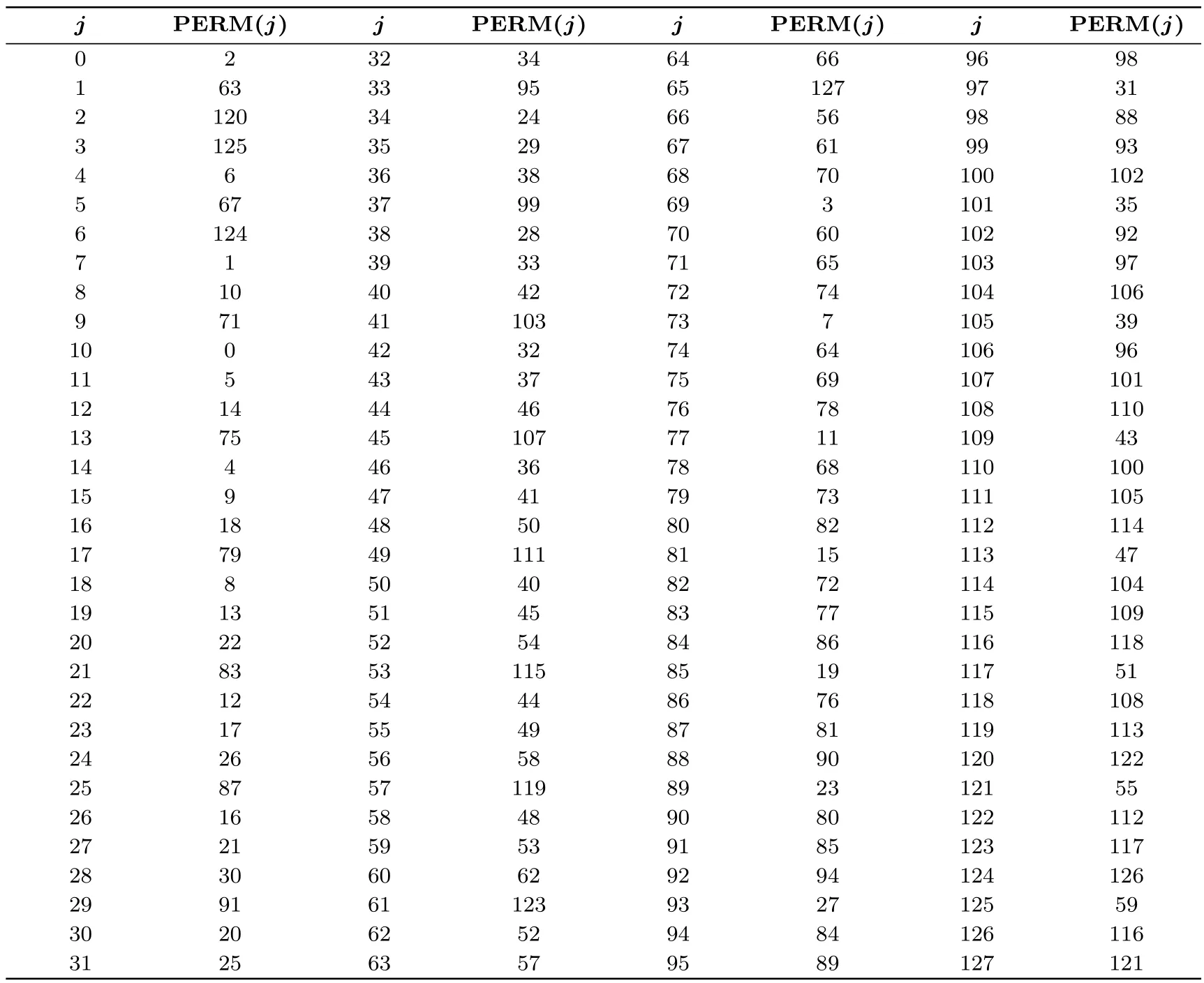
表3 ANT-256的PERMTable 3 PERM in ANT-256

对于ANT-256:

2.2 密钥生成算法

ANT分组密码算法可采用2n或者4n比特长度的主密钥K,因此使用如下2种基于线性反馈移位寄存器(LFSR)的密钥扩展方案.

对于ANT-2n/2n:2n比特的主密钥K=k2n-1‖k2n-2‖···‖k0可以分成2个字(高n比特和低n比特),

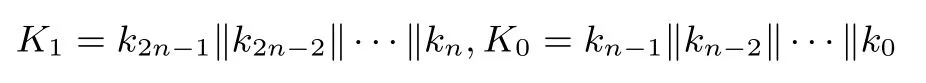
K1,K0作为图2中LFSR的初始状态.每次根据第i轮子密钥Ki和第(i+1)轮子密钥Ki+1可以更新出第(i+2)轮子密钥Ki+2,其中0≤i＜R-2.LFSR在进行更新时,(i+1)作为轮常数,当前寄存器Ki+1中的状态经过Feistel结构的A操作(见图3)迭代更新3次.注意不同分组下,A操作的输入分成了8个比特的变量,X7‖···‖X0,其中的移位参数(t0,t1)在表4中给出.如下给出ANT-2n/2n密钥生成算法的更新表达式:

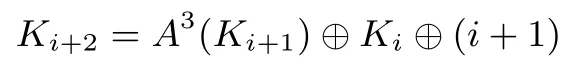
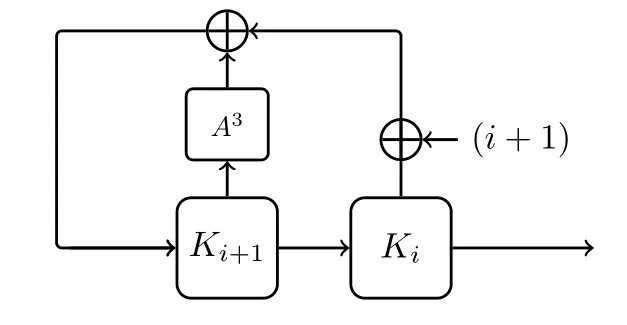
图2 ANT-2n/2n密钥生成算法Figure 2 Key schedule of ANT-2n/2n

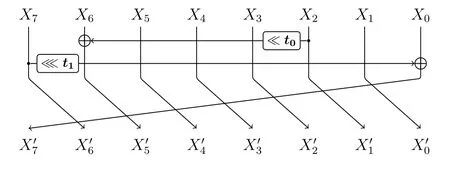
图3 A操作Figure 3 Operation A

表4 A操作中的(t0,t1)移位参数Table 4 Parameters(t0,t1)in A operation

对于ANT-2n/4n:类似的,4n比特的主密钥K=k4n-1‖k4n-2‖···‖k0可以分成4个字,

K3,K2,K1,K0作为图4中LFSR的初始状态.每次根据第i轮子密钥Ki,第(i+1)轮子密钥Ki+1,第(i+2)轮子密钥Ki+2和第(i+3)轮子密钥Ki+3可以更新出第(i+4)轮子密钥Ki+4,其中0≤i＜R-4.LFSR在进行更新时,(i+1)作为轮常数,当前寄存器Ki+3中的状态经过Feistel结构的A操作(见图3)迭代更新3次.注意不同分组下,A操作的输入分成了8个比特的变量,X7‖···‖X0,移位参数同样见表4.如下给出ANT-2n/4n密钥生成算法的更新表达式:

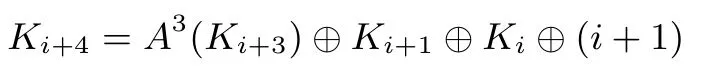
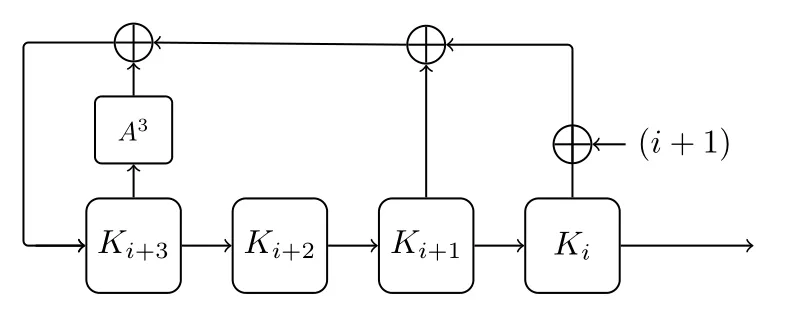
图4 ANT-2n/4n密钥生成算法Figure 4 Key schedule of ANT-2n/4n

3 ANT算法设计原理

3.1 Feistel结构结合Exp and-then-comp ress思想

Feistel结构是一种经典的分组密码结构.与SPN结构相比,具有加解密一致的优势,有利于减小硬件实现代价.但由于Feistel结构每次只更新部分数据,导致基于Feistel结构的算法同基于SPN结构的算法相比扩散速度较慢.因此,ANT算法在设计的过程中,采用了Expand-then-compress的设计思想,将算法的一支先进行扩展复制,再分别进入两个非线性函数G0和G1.一方面,可以增加扩散速度；另一方面,可以并行处理以减小轮函数时延.这种设计思想被许多分组密码所采用,如DES[13]、PICARO[14]和SIMON[15]等.

3.2 比特级非线性函数G0/G1

非线性函数G0和G1均为2层结构,并且均采用比特级的设计,仅包含AND,Rotation和XOR三种操作.相比于传统的S盒算法,这样可以极大地减小硬件面积,同时针对侧信道防护的代价很小.除去中间一层所采用的相同置换PERM,G0和G1分别由相近的nibble基本单元组成,如图5.

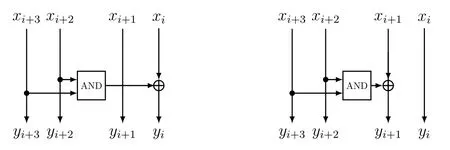
图5 G0(左)和G1(右)中的nibble基本单元Figure 5 Basic nibbles in G0(left)and G1(right)

由于G0和G1中的nibble基本单元非常简单,仅有1个非线性操作AND和1个线性操作XOR组成.因此,置换PERM的选择直接影响到算法的安全性,其选择的原则有以下几点:

·保证每个比特经过G0/G1后都经过非线性操作.

·保证经过压缩操作之后每个比特的代数度至少为2次.

·结合循环移位参数(s0,s1)1循环移位参数(s0,s1)的选取主要是避免相关性对安全性评估造成影响,所以s0,s1的差值非4的倍数.通过穷搜在小分组的特定轮数下所有循环移位参数,以对差分/线性抵抗能力为指标进行选取,最终确定为(3,16),并将此参数应用到大分组上,发现仍能达到较好的安全性.达到较好的扩散效果.

·方便进行bitslice软件实现.

从结果看,ANT算法的各个分组均达到了较好的扩散性.其中,ANT-128的全扩散轮数为5轮,ANT-256的全扩散轮数为7轮.考虑到ANT算法的轻量级设计和Feistel结构,这个扩散速度已经较快(SIMON-128算法的全扩散轮数为13轮).

3.3 密钥生成算法

ANT算法的密钥生成算法在设计时主要考虑以下几点:(1)硬件代价小；(2)扩散性好；(3)匹配轮函数的时延.因此,我们采用了近年来逐渐被广泛采用的线性的密钥生成算法,通过LFSR的形式来更新子密钥.结合Feistel结构的A操作,通过迭代多次来换取较大硬件面积才能够达到的扩散效果,这种方式最早运用在基于SPN结构的CUBE分组密码算法[16]中.我们针对ANT算法进行扩展,在保证较好扩散效果的同时,进一步减小硬件代价(比如令变量经过t0移位操作后仅剩下1比特).

4 ANT算法安全性分析

4.1 差分分析和线性分析

差分分析(DC)[17]和线性分析(LC)[18]均是经典的密码分析方法.为了展示ANT系列分组密码算法对差分攻击和线性攻击的抵抗能力,在表5中给出了不同分组最优的差分特征和线性特征的搜索情况(利用SAT/SMT技术进行搜索).由此可以得到,ANT-128不存在超过27轮的有效差分或线性特征(28轮的差分特征的下界为49+42+42=133),ANT-256不存在超过47轮的有效差分或线性特征(45×6=270).

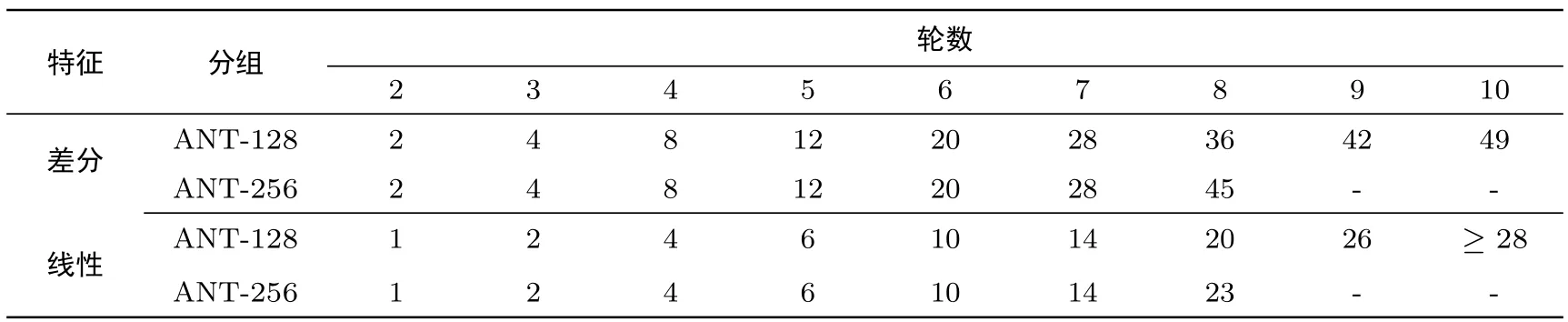
表5 ANT算法差分特征和线性特征搜索结果(概率以-log2 p形式给出,线性特征使用相关度)Table 5 Searching results of differential/linear characteristics for ANT(probability is given as-log2 p and the correlation is used for linear trail)

我们还对ANT算法的differential和linear hull效应进行了测试,结果发现ANT系列算法的differential和linear hull效应不显著.根据搜索得到ANT-128的6轮最优差分路线(概率为2-20)和6轮最优线性路线(相关性为2-10).首先,利用SAT/SMT技术进行路线堆积[19],发现理论堆积的效果不显著.然后,随机取100个密钥,在每个密钥下选取224的数据量对路线进行验证.实验结果与理论堆积的结果相符合.因此,ANT系列分组密码算法有较好的差分和线性抵抗能力,设置的轮数足够抵抗差分攻击和线性攻击.

4.2 不可能差分分析和零相关线性分析

不可能差分分析(IDC)[20,21]和零相关线性分析(ZC)[22]分别是对差分分析和线性分析方法的拓展.同样利用SAT/SMT技术,我们利用比特级的搜索方式[23]对不同分组ANT的不可能差分和零相关线性路线进行搜索,结果如表6.

表6 ANT算法搜索到的最长IDC和ZC区分器轮数Table 6 Longest IDC and ZC distinguishers found for ANT

因此,不可能差分和零相关线性攻击对ANT系列分组密码算法不够成威胁.如下给出一条ANT-128的9轮IDC路线示例:

4.3 积分分析

积分攻击[24]利用特定的明文集合在密文处的非随机的代数性质来区分随机置换和目标密码算法.本文利用SAT/SMT技术,基于比特级的可分性[25]对不同分组的ANT算法进行积分路线搜索.对于ANT-128,经搜索发现不存在超过16轮的积分路线；对于ANT-256,经过搜索发现不存在超过21轮的积分路线.因此,ANT系列分组密码算法的轮数足以抵抗积分攻击.

5 ANT算法性能分析

5.1 软件性能

我们对ANT系列分组密码算法进行了64-bit Windows下的CBC单路加/解密速度测试,CBC多路解密速度测试和32-bit ARM下的CBC单路加/解密速度测试.测试过程采用256字节短数据进行一次CBC模式下的加密,包含了密钥生成算法的时间.如此进行多次并且每次加密均运行一次完整的密钥生成算法,最后取速率的平均值.测试环境分别为:

·Windows7,i7-6700,8 GB DDR4 2400M.VS 2017,x64,avx2.

·STM32F103ZET6,主频72 MHz.EWARM8.2.

具体测试结果见表7.可以发现,针对bitslice而设计的比特级轮函数结构,使ANT算法具有较好的多路运行速率.

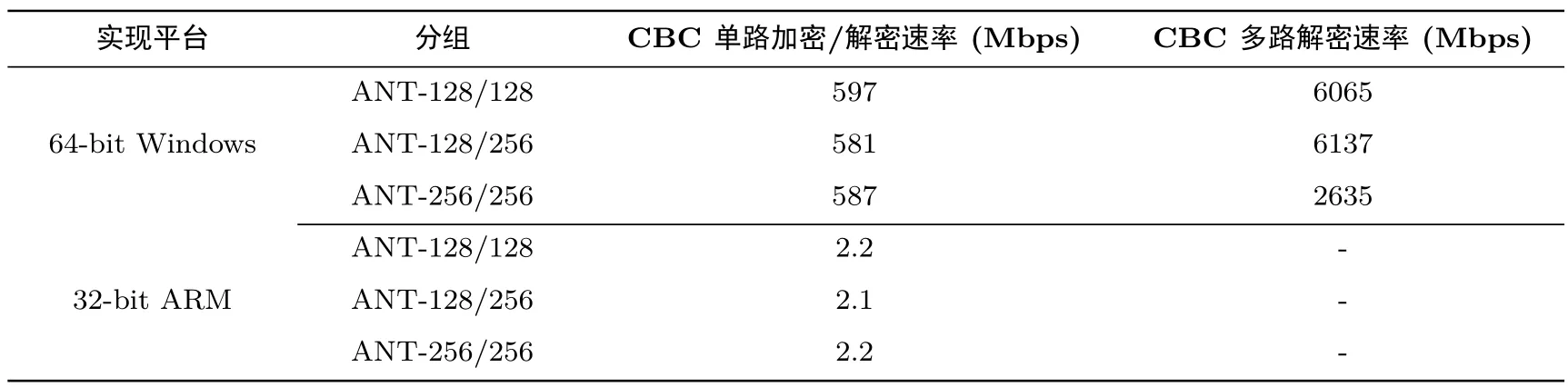
表7 ANT算法软件速率优化C实现Table 7 Software performance of ANT under C optimized implementations

5.2 硬件性能

我们利用Verilog HDL语言对ANT系列分组密码算法进行了基于单轮的实现,采用32个分组数据进行加/解密,且至少调用1次密钥扩展算法.硬件仿真数据如表8.

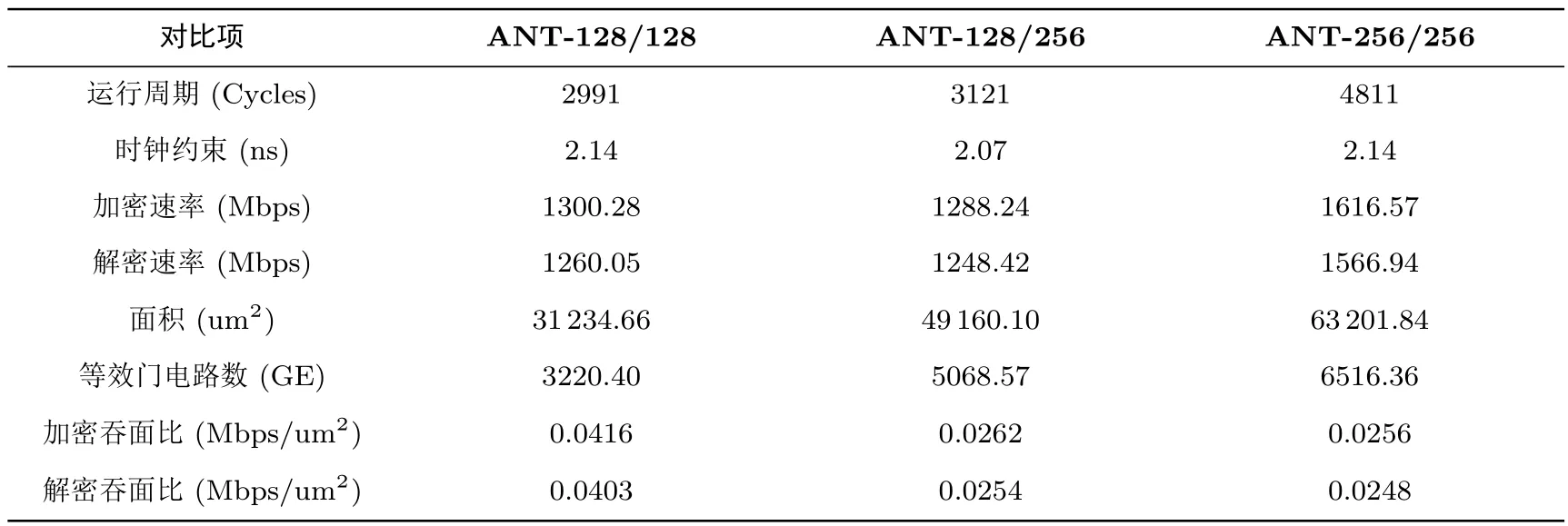
表8 基于单轮实现的硬件指标(综合采用HJTC 110 nm标准元件库)Table 8 Hardware performance for round-based implementations(synthesized with HJTC 110 nm standard cell libarary)

可以观察到,得益于简单的AND-RX结构,ANT算法的硬件实现代价非常小,再结合上Feistel结构加解密一致的特性,使得ANT算法具有优异的硬件实现性能,各版本均具有较高的吞面比.ANT-128/128分组加解密基于轮实现仅需硬件面积3220 GE.

6 总结

本文给出了一款新的分组密码算法—ANT,其设计目标是:相比于国际上传统的分组密码算法,更适合轻量级实现,具有优异吞面比,便于侧信道防护且代价小,同时适合bitslice软件多路实现的分组密码算法.因此在设计过程中,ANT算法采用了经典的Feistel结构并结合Expand-then-compress的设计理念.在关键的轮函数上,采用了比特级的设计(与操作,异或操作,置换操作和循环移位操作),与传统利用S盒作为非线性组件的算法相比,其硬件面积小且侧信道防护代价小.一些组件如比特级置换的选取也考虑了软件多路bitslice的实现性能.密钥生成算法的设计,一方面采用了近年来应用广泛的线性的密钥生成算法,达到了较好的扩散性.另一方面,硬件实现代价小并且匹配了轮函数的时延.针对现有常见攻击方法的安全性分析也表明ANT系列分组密码算法具有足够的安全冗余.

附录

图6 ANT-128的G0Figure 6 G0 in ANT-128

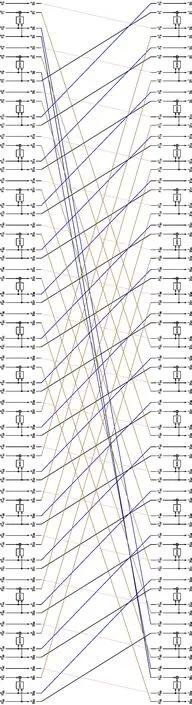
图7 ANT-128的G1Figure 7 G1 in ANT-128