SMBA分组密码算法

王克,贾文义,黄念念

兴唐通信科技有限公司,北京100191

1 算法描述

1.1 概述

SMBA是一个分组密码算法,分组长度支持128和256比特.分组长度为128比特时密钥长度支持128和256比特,分组长度为256比特时密钥长度为256比特.分组长度(比特数,记为BL)和密钥长度(比特数,记为KL)对应的SMBA的迭代轮数(记为N)如表1所示.

表1 SMBA算法的三个版本和迭代轮数Table 1 Three versions of SMBA and the iterated round number

分组长度为128比特的SMBA记为SMBA-128,其中密钥长度为128或256比特时也分别记为SMBA-128-128或SMBA-128-256.分组长度为256比特的SMBA记为SMBA-256,也可记为SMBA-256-256.

1.2 符号、运算符和约定

1.2.1 符号和运算符列表

0x 用前缀0x表示16进制数 = 赋值运算符,也可表示相等

MT向量或矩阵M的转置 ⊕ 逐比特异或运算符

0nn比特0组成的比特串 BL 分组长度,比特数.

KL 密钥长度,比特数 N 迭代轮数

MSBt(x) 由x的最左(即最高)t比特组成的t比特数

LSBt(x) 由x的最右(即最低)t比特组成的t比特数

1.2.2 比特、字节和子块顺序约定

所有数据变量用最高比特(或子块)在左边,最低比特(或子块)在右边表示,而且从左到右从0开始编号.例如,一个n比特数从左到右分别称为它的第0比特、第1比特、第2比特、···、第n-1比特.当一个变量被分成几个子块时,最左边(最高)子块由原始数据的最高部分组成,等等一直到最低.

当密码算法的输入(或输出)是字节流时,我们按地址小的是高位(即左边),地址大的是低位(即右边)的顺序把每4(或2)个字节组成一个32(或16)比特字.32(或16)比特字之间的顺序是先左后右,即存储时,左边地址小,右边地址大.

约定比特串x0‖x1‖x2‖···‖xn-1、整数2n-1x0+2n-2x1+2n-3x2+···+2xn-2+xn-1、行向量(x0,x1,x2,···,xn-1)、列向量(x0,x1,x2,···,xn-1)T是等价的,可互相转化.

1.3 加解密过程

1.3.1 加密过程

算法1 SMBA加密算法1.将BL比特明文plaintext分为各BL/2比特的左、右两部分x0和x1,即plaintext=x0‖x1 2.对于i=0,1,···,N-1 xi+2=xi⊕F[EK i](xi+1)3.xN+1和xN连接成BL比特密文ciphertext,即ciphertext=xN+1‖xN.

其中,F为轮函数,EKi(0≤i≤N-1)为N个BL/2比特的加密子密钥,由密钥Key用密钥扩展算法派生.

1.3.2 解密过程

算法2 SMBA解密算法1.将BL比特密文ciphertext分为各BL/2比特的左、右两部分x0和x1,即ciphertext=x0‖x1 2.对于i=0,1,···,N-1 xi+2=xi⊕F[DK i](xi+1)3.xN+1和xN连接成BL比特明文plaintext,即plaintext=xN+1‖xN.

其中,F为轮函数,DKi(0≤i≤N-1)为N个BL/2比特的解密子密钥,由密钥Key用密钥扩展算法派生.

解密子密钥与加密子密钥满足如下关系:DKi=EKN-1-i(0≤i≤N-1).

1.4 轮函数及其组件

1.4.1 轮函数F[K]

轮函数y=F[K](x)的输入是一个BL/2比特数x和一个BL/2比特子密钥K,输出是一个BL/2比特数y,y=F[K](x)=L(S(P(W[K](x)))),即F[K]=L◦S◦P◦W[K](参见图1、图2).各变换W[K]、P、S、L见下面定义.

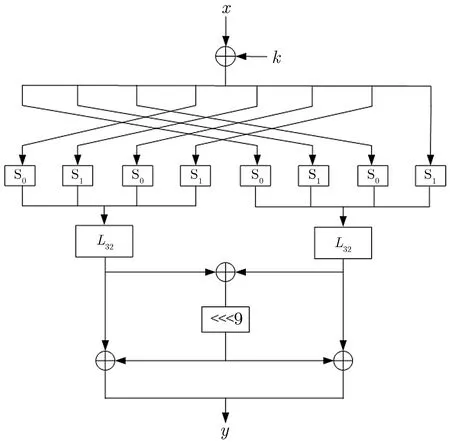
图1 SMBA-128轮函数Figure 1 Round function of SMBA-128

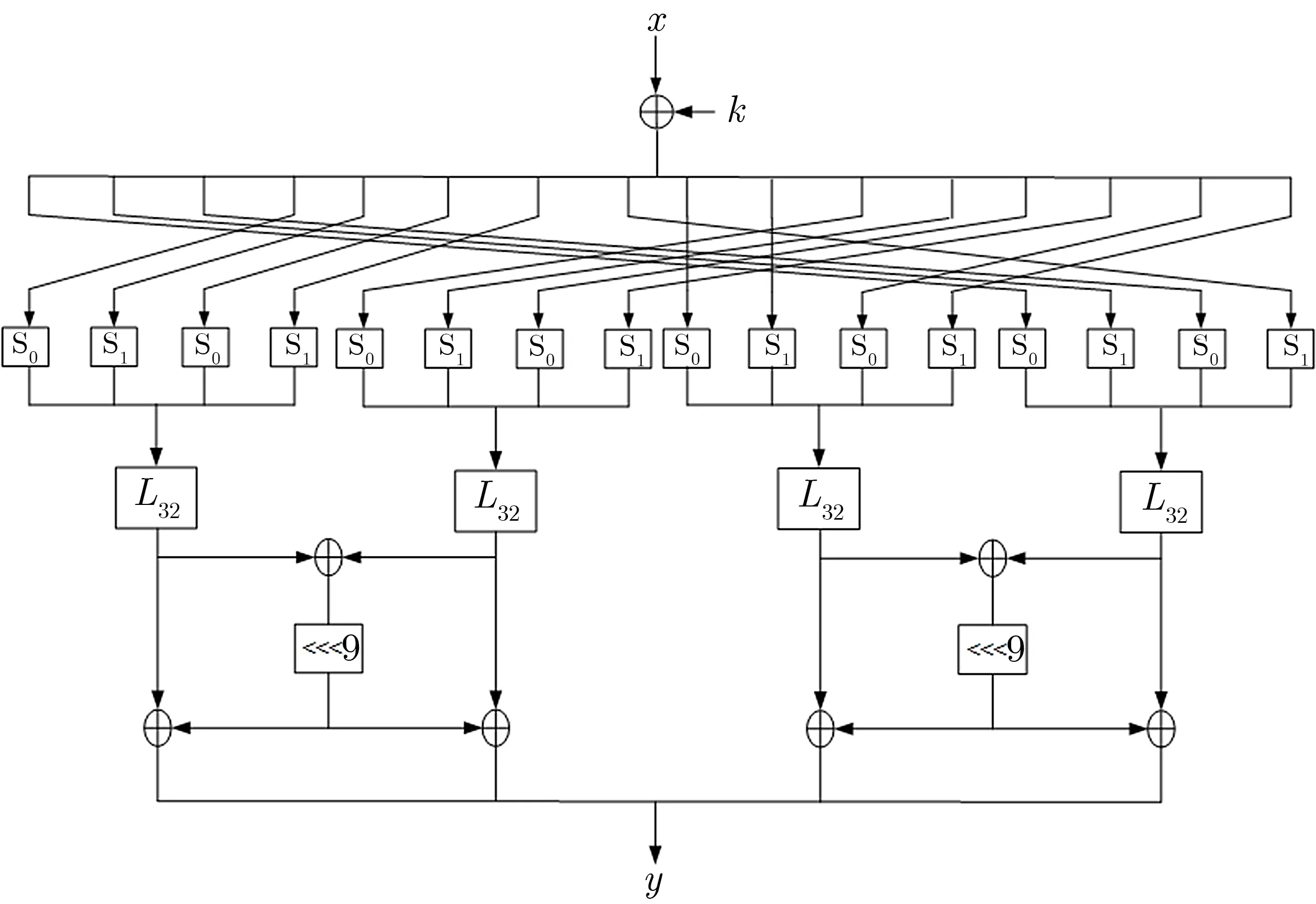
图2 SMBA-256轮函数Figure 2 Round function of SMBA-256

1.4.2 白化变换W[K]

对于BL/2比特数x和BL/2比特子密钥K,W[K](x)=x⊕K.

1.4.3 换位变换P

换位变换P对于SMBA-128使用换位变换P64,对于SMBA-256使用换位变换P128.

P64是一个64比特数到64比特数的变换,具体为:把64比特数x分为8个8比特数xi,0≤i≤7,即x=x0‖x1‖···‖x7,令yi=xτ(i),则

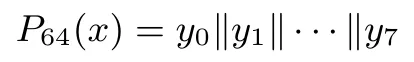
其中τ(i),0≤i≤7,依次为:3,4,5,6,0,1,2,7.

P128是一个128比特数到128比特数的变换,具体为:把128比特数x分为16个8比特数xi,0≤i≤15,即x=x0‖x1‖···‖x15,令yi=xπ(i),则

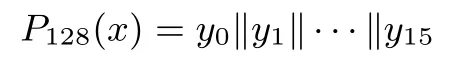
其中π(i),0≤i≤15,依次为:3,4,5,6,10,11,12,13,8,9,14,15,0,1,2,7.

1.4.4 代替变换S

代替变换S对于SMBA-128使用代替变换S64,对于SMBA-256使用代替变换S128.

S32是一个32比特数到32比特数的变换,具体为:将32比特数x分为4个8比特数,即x=x0‖x1‖x2‖x3,令

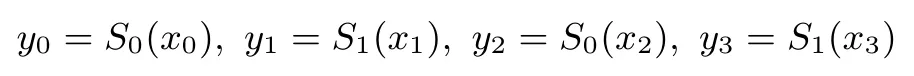
则S32(x)=y0‖y1‖y2‖y3,其中,S0、S1都是8比特到8比特的代替盒(S盒).

S64是一个64比特数到64比特数的变换,具体为:将64比特数x分为2个32比特数,即x=x0‖x1,

令

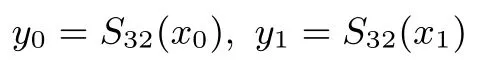
则S64(x)=y0‖y1.

S128是一个128比特数到128比特数的变换,具体为:将128比特数x分为2个64比特数,即x=x0‖x1,令

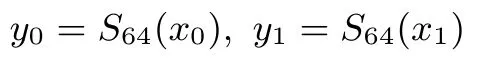
则S128(x)=y0‖y1.

1.4.5 线性变换L

线性变换L对于SMBA-128使用线性变换L64,对于SMBA-256使用线性变换L128.

L32是32比特数到32比特数的变换,具体为:将32比特数x分为4个8比特数,即x=x0‖x1‖x2‖x3,令

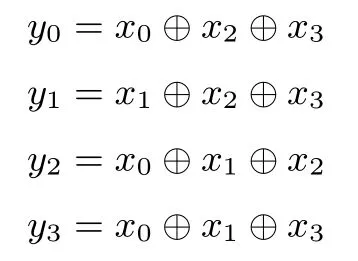
则L32(x)=y0‖y1‖y2‖y3.

L64是一个64比特数到64比特数的变换,具体为:将64比特数x分为2个32比特数,即x=x0‖x1,令

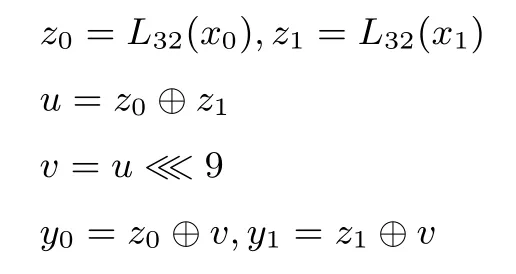
则L64(x)=y0‖y1.

L128是一个128比特数到128比特数的变换,具体为:将128比特数x分为2个64比特数,即x=x0‖x1,令

则L128(x)=y0‖y1.

1.5 密钥扩展

密钥扩展算法根据密钥Key,生成N个BL/2比特加密子密钥EKi和N个BL/2比特解密子密钥DKi,0≤i≤N-1.

常数C为自然对数的底e的小数部分的前128比特,用16进制表示为

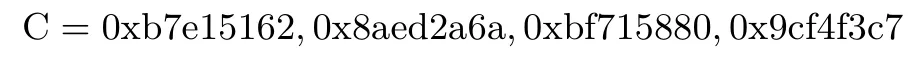
1.5.1 变换α、β、γ

变换α、β、γ对于SMBA-128-128和SMBA-128-256使用α64、β64、γ64,对于SMBA-256-256使用α128、β128、γ128.

α64、β64、γ64都是64比特到64比特的变换,分别如下.

把64比特数x分为8个8比特数xi,0≤i≤7,即x=x0‖x1‖···‖x7,令yi=xalpha64(i),则

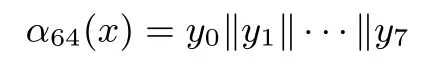
其中alpha64(i),0≤i≤7,依次为:2,7,1,4,6,3,5,0.

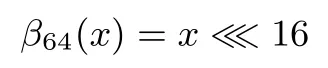
把64比特数x分为8个8比特数xi,0≤i≤7,即x=x0‖x1‖···‖x7,令yi=Simod2(xi),则

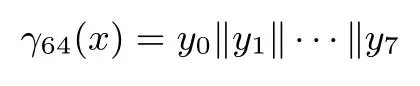
α128、β128、γ128都是128比特到128比特的变换,分别如下.

把128比特数x分为16个8比特数xi,0≤i≤15,即x=x0‖x1‖···‖x15,令yi=xalpha128(i),则

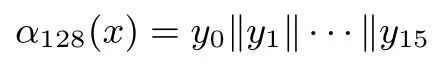
其中alpha128(i),0≤i≤15,依次为:13,4,12,0,8,10,2,6,14,3,11,15,7,9,1,5.

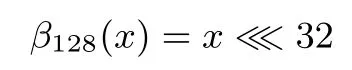
把128比特数x分为16个8比特数xi,0≤i≤15,即x=x0‖x1‖···‖x15,令yi=Simod2(xi),

则

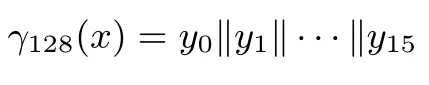
1.5.2 SMBA-128-128的子密钥生成

算法3 SMBA-128-128子密钥生成算法1.U0=MSB 64(Key),V0=LSB 64(Key)2.D=N‖Block Len‖Key Len‖040,这里Block Len=BL/8为分组长度(字节数),Key Len=KL/8为密钥长度(字节数),N、Block Len、Key Len都用8比特表示3.C0=MSB 64(C)⊕D 4.进行N个密钥扩展轮变换(参见图3),即对于i=0到N-1 Xi=Ui⊕Ci Yi=α64(Xi)Zi=γ64(Yi)EK i=DK N-1-i=Zi Ui+1=Zi⊕Vi Vi+1=β64(Ui)Ci+1=Ci⋘23

1.5.3 SMBA-128-256的子密钥生成

算法4 SMBA-128-256子密钥生成算法1.U0,0‖U0,1‖U0,2‖U0,3=Key,其中U0,i的长度都是64比特,0≤i≤3；2.D=N‖Block Len‖Key Len‖04 0,这里Block Len=BL/8为分组长度(字节数),Key Len=KL/8为密钥长度(字节数),N、Block Len、Key Len都用8比特表示3.C0=MSB 6 4(C)⊕D 4.进行N个密钥扩展轮变换(参见图4),即对于i=0到N-1 Xi=Ui,0⊕Ci Yi=α6 4(Xi)Zi=γ6 4(Yi)EK i=DK N-1-i=Zi U i+1,0=Z i⊕U i,1 U i+1,1=U i,2 U i+1,2=U i,3 Ui+1,3=β6 4(Ui,0)Ci+1=Ci⋘23

1.5.4 SMBA-256-256的子密钥生成

算法5 SMBA-256-256子密钥生成算法1.U0=MSB 128(Key),V0=LSB 128(Key)2.D=N‖Block Len‖Key Len‖0104,这里Block Len=BL/8为分组长度(字节数),Key Len=KL/8为密钥长度(字节数),N、Block Len、Key Len都用8比特表示3.C0=C⊕D 4.进行N个密钥扩展轮变换(参见图3),即对于i=0到N-1 Xi=Ui⊕Ci Yi=α128(Xi)Zi=γ128(Yi)EK i=DK N-1-i=Zi Ui+1=Zi⊕Vi Vi+1=β1 28(Ui)Ci+1=Ci⋘57

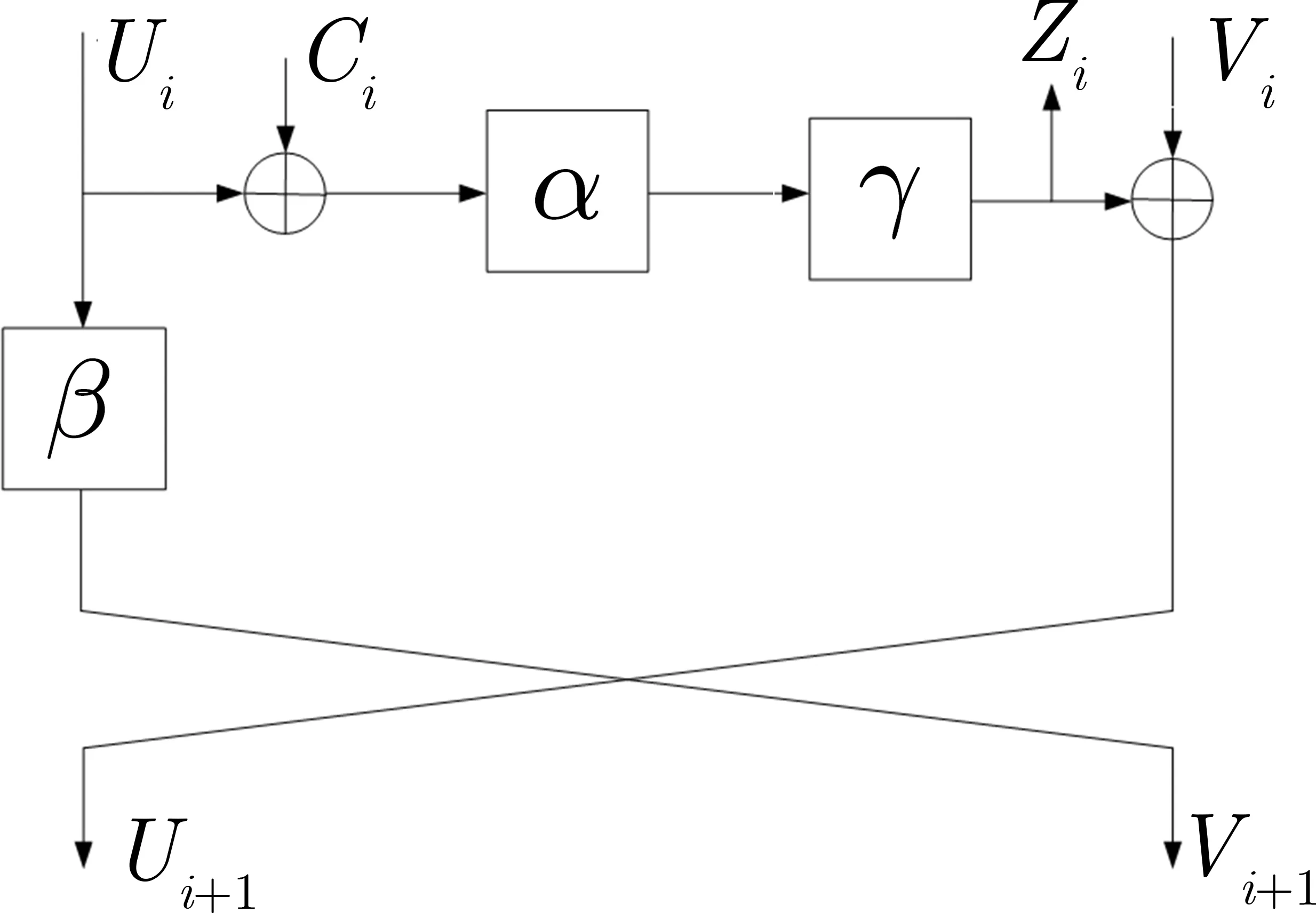
图3 SMBA-128-128和SMBA-256-256密钥扩展过程Figure 3 Key schedule of SMBA-128-128 and SMBA-256-256

1.6 S盒S0和S1

用16进制表示的代替盒S0和S1分别如下:

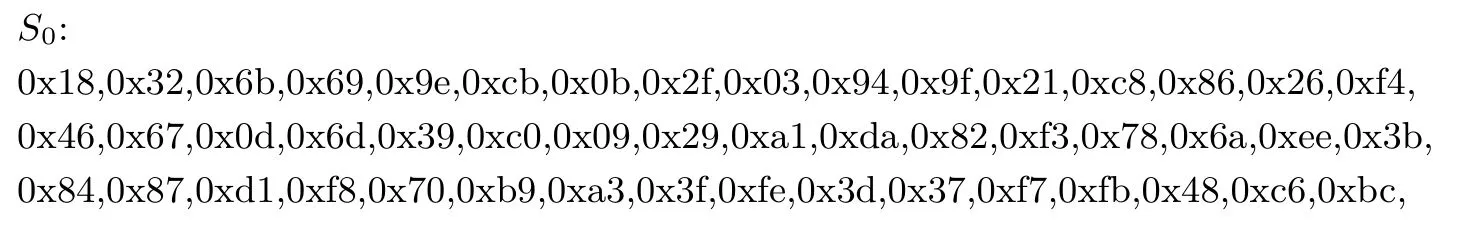
1.6.1 S0构造过程

设Z是GF(2)中的不可约多项式z2+z+1的根,则(Z,1)是GF(22)在GF(2)上的一组多项式基.

设Y是GF(22)中的不可约多项式y2+y+Z(因为tr4/2(Z)=Z+Z2=1)的根,则(Y,1)是GF(24)在GF(22)上的一组多项式基,(ZY,Y,Z,1)是GF(24)在GF(2)上的一组基.有

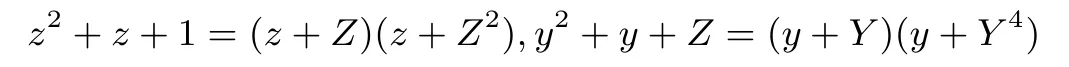
GF(22)在基(Z,1)上的乘法:

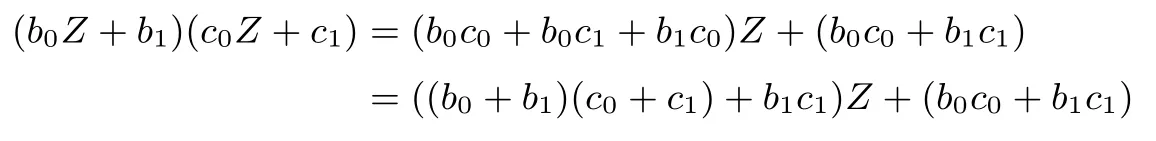
GF(22)在基(Z,1)上的乘法:

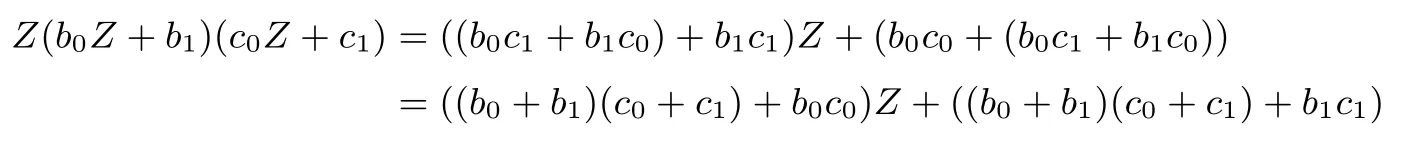
GF(24)在基(Y,1)上的乘法:

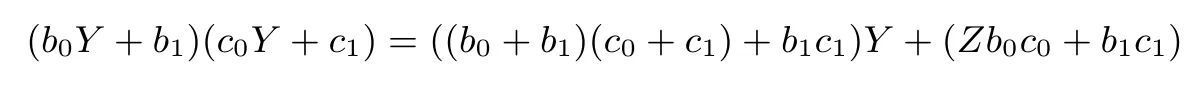
设S0的8比特输入为x,则如算法6计算S0的8比特输出S0[x]:

算法6 S0构造算法(见图5)1.a=M0×(x⊕Con0),将a分为2个4比特a0、a1,即a=a0‖a1 2.b=a0⊗a1 3.c=b13 4.d=c⊗a1 5.e0=Q0[a0],e1=Q1[a1]6.若c为0,则f=e0‖e1；否则f=d‖c 7.S0[x]=M1×(f)⊕Con1

其中,符号⊗表示GF(24)在基(ZY,Y,Z,1)上的乘法,×表示矩阵与列向量相乘.b13表示GF(24)在基(ZY,Y,Z,1)上b的13次幂,该变换用16进制表示为:

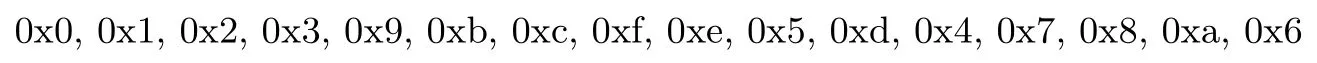
两个4比特S盒Q0、Q1分别为:

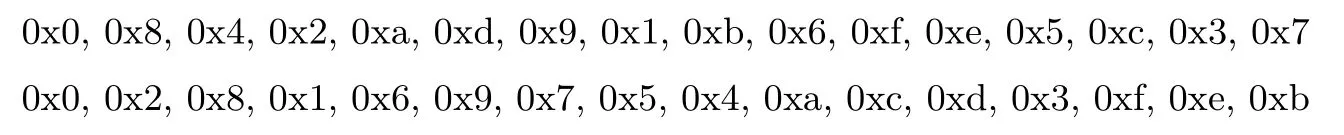
两个矩阵M0和M1都是置换矩阵,M0的第i行第τ0(i)列为1,其余为0；M1的第i行第τ1(i)列为1,其余为0；0≤i≤7.τ0和τ1分别为:

两个8比特常数分别为:Con0=0x52,Con1=0x4d.

1.6.2 S1构造过程

当q=2n时,(α,αq)是GF(q2)在GF(q)上的一组正规基,当且仅当trq2/q(α)=α+αq/=0.设Z是GF(2)中的不可约多项式z2+z+1的根,则(Z2,Z)是GF(22)在GF(2)上的一组正规基.

设Y是GF(22)中的不可约多项式y2+y+Z(因为tr4/2(Z)=1)的根,则(Y4,Y)是GF(24)在GF(22)上的一组正规基,(Z2Y4,ZY4,Z2Y,ZY)是GF(24)在GF(2)上的一组基.

设X是GF(24)中的不可约多项式x2+x+Z2Y4(因为tr16/4(Z2Y4)=1)的根,则(X16,X)是GF(28)在GF(24)上的一组正规基.有z2+z+1=(z+Z)(z+Z2),y2+y+Z=(y+Y)(y+Y4),x2+x+Z2Y4=(x+X)(x+X16).约定0-1=0.

GF(22)在基(Z2,Z)上的乘法:

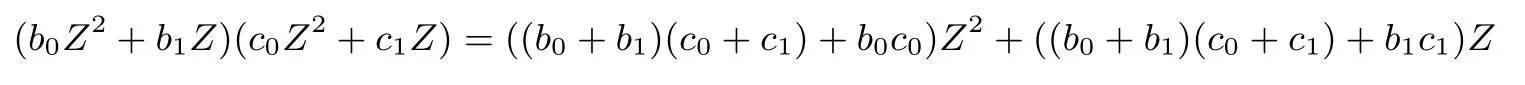
GF(22)在基(Z2,Z)上的乘法:

GF(24)在基(Y4,Y)上的乘法:

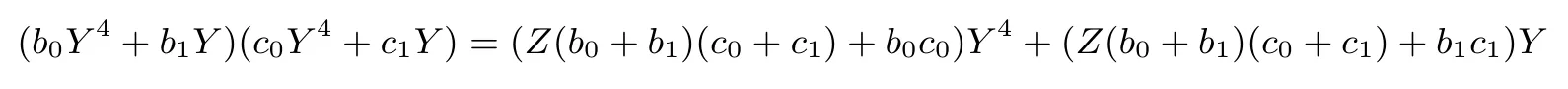
GF(24)在基(Y4,Y)上的乘法:

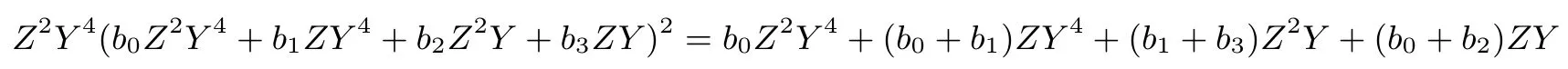
GF(28)在基(X16,X)上的求逆:

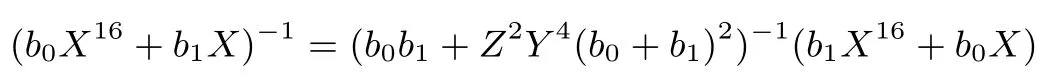
算法7 S1构造算法(见图6)1.a=M2×(x⊕Con2),将a分为2个4比特a0、a1,即a=a0‖a1 2.b0=a0⊕a1,b1=a0⊗a1 3.c=Z 2 Y 4⊗b2 0 4.d=c⊕b1 5.e=d-1 6.f0=e⊗a1,f1=e⊗a0 7.S1[x]=M3×(f0‖f1)⊕Con3

图5 S0结构图Figure 5 Construction of S0

图6 S1结构图Figure 6 Construction of S1

设S1的8比特输入为x,则如算法7计算S1的8比特输出S1[x].

⊗表示GF(24)在基(Z2Y4,ZY4,Z2Y,ZY)上的乘法.d-1表示GF(24)在相同基上d的逆,该变换用16进制表示为:

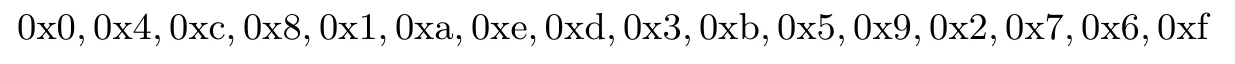
两个矩阵M2和M3都是置换矩阵,M2的第i行第τ2(i)列为1,其余为0；M3的第i行第τ3(i)列为1,其余为0；0≤i≤7.τ2和τ3分别为:

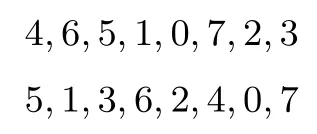
两个8比特常数分别为:Con2=0xa4,Con3=0x5f.

2 设计原理

2.1 加解密过程设计原理

整体结构采用标准Feistel结构,其优点在于:

(1)加解密过程除子密钥的顺序外完全相同,降低软硬件的实现代价.

(2)与SPN结构相比,其使用的硬件资源更小.更易做资源与效率的折中.

轮函数使用SP结构,其主要考虑如下:

(1)安全性和有效性的综合性能更高.

(2)基本运算为查表、固定位数的循环移位,以及异或等逻辑运算,易于硬件实现以及软件的查大表快速实现.

通过整体结构以及轮函数的设计,SMBA算法具备软硬件多种平台上实现的有效性和灵活性.SMBA-128与SMBA-256共用主要的密码部件,一起实现所付出的额外代价低.同时,算法可以准确评估抵抗差分攻击、线性攻击、代数攻击和积分攻击等已知攻击所需的轮数,安全界清晰.所选迭代轮数确保算法有较大的安全冗余.在算法设计上不隐藏任何“后门”.

2.2 密钥扩展设计原理

(1)一次加密子密钥、解密子密钥的生成速度分别高于一个分组加密、解密运算的速度.这样可以尽量降低在短消息条件下密钥扩展过程对算法性能的影响.

(2)加密子密钥和解密子密钥均可在加解密过程中实时计算,且与加解密过程相比硬件实现电路深度更小,可以为硬件实现提供更多的灵活性、更好的有效性.

综合以上的考虑,我们设计了SMBA的密钥扩展算法.SMBA-128-128和SMBA-256-256密钥扩展的结构本质上是广义Feistel结构[1],SMBA-128-256密钥扩展是广义Feistel结构的推广.此外密钥扩展与加解密过程共用S盒S0和S1,在特定场景下可通过复用的方式降低硬件资源.

2.3 S盒设计原理

SMBA使用8比特S盒,主要的考虑是8比特S盒逻辑更加复杂,相比较4比特S盒,其抵抗潜在的攻击能力更强.在非轻量级环境下,一般这样的S盒的实现代价是可以接受的.

SMBA所用的8比特S盒S0和S1通过两种不同的方式构造生成(设计思想分别参考了文献[2,3]和文献[4]),其用到的非线性运算为查4比特S盒,GF(24)上的乘法,以及多路选择器.相比于随机产生然后进行检测生成的S盒(还包括梯度下降、遗传算法等的迭代优化),S0和S1有如下优势:

(1)更好的密码强度指标.

(2)更优的硬件实现性能.在4比特S盒的选取上,我们尽量采用硬件资源小的S盒,同时通过选取特定的基,使得GF(24)上的乘法运算可以节省一定的资源,可以追求更小的面积.我们也有追求更小深度的实现方式,更适用于追求更高速度的环境.

(3)更低的侧信道攻击防护代价.在4比特S盒的选取上,我们除了实现资源外,更考虑了其中与门的个数.通过采用具有更少与门的S盒,并配以搜索得到的前后仿射变换,我们获得的S盒在抵抗侧信道攻击的指标更优.

(4)可清楚地表明S0和S1的设计均无后门.

2.4 线性变换和换位变换设计原理

由于64比特的MDS线性变换软硬件实现代价较大,关键路径深,资源占用多,我们希望在密码学性质和实现代价之间取得折中.SMBA线性变换的主要设计思想是将少量简单的线性变换组合起来,获得具有更高分支数、更好密码学性质的大规模线性变换.我们采用了两个简单的L32变换,以及一个L-M结构的简单线性变换,成功构造了一个新的变换L64,其具有如下的特性:

(1)L64、的差分分支数和线性分支数都为6.

(2)L64、都将1个非零字节变换到7个非零字节.

(3)不是面向字节的运算.

(4)各种软件平台(8/32/64比特)及硬件都可有效实现.

对SMBA-256,换位变换P128不仅确保算法的加解密过程都形成一个整体,并且使得算法抗差分、线性等攻击能力显著提升.

3 安全性分析

3.1 整体结构安全性

SMBA的整体结构采用标准Feistel结构,Feistel结构已广泛应用于分组密码算法的设计中,具有很好的结构安全性,可证明:在轮函数是伪随机函数的假设下,3轮Feistel结构是伪随机置换,4轮Feistel结构是超伪随机置换.

另外,对于SMBA-256,若假设函数L64◦S64为伪随机函数(相对于轮函数是伪随机函数的假设是更弱、更合理的假设),则可证明:4轮是伪随机置换,6轮是超伪随机置换.

3.2 密码部件安全性

3.2.1 非线性部件安全性

SMBA算法使用了2个8比特到8比特的S盒S0和S1,其密码学性质如表2.

表2 S0和S1的密码学性质Table 2 Cryptographic property of S0 and S1

其中,透明阶、改进的透明阶、DPA信噪比、Hamming重量的混乱系数方差是为了评估S盒抵抗侧信道攻击(SCA)的能力引入的指标.通常认为,透明阶、改进的透明阶和DPA信噪比越小,表明S盒抵抗差分能量攻击(DPA)的能力越强；Hamming重量的混乱系数方差越大,表明S盒抵抗侧信道攻击的能力越强.AES算法S盒的透明阶、改进的透明阶、DPA信噪比、Hamming重量的混乱系数方差分别为7.860、6.916、9.600、0.111,根据表2知,S0和S1比AES算法的S盒具有更强的抗侧信道攻击的能力(唯一的例外是AES算法S盒改进的透明阶小于S1改进的透明阶).

3.2.2 线性部件安全性

SMBA的线性变换有L32、L64、L128三种.

L32具有以下性质:

(1)L32是对合变换,即L32(L32(x))=x；

(2)L32的差分分支数和线性分支数都是4.

L64具有以下性质:

(1)L64的差分分支数和线性分支数都是6；

(2)y=L64(x),w(x)=1时,w(y)≥7；

(3)y=LT64(x),w(x)=1时,w(y)≥7；

(4)(y0‖y1)=L64(x0‖x1),若x0=0,x1/=0,则y0/=0,且y1=0⇔ x1=0xffffffff；

(5)(y0‖y1)=L64(x0‖x1),若x0/=0,x1=0,则y1/=0,且y0=0⇔ x0=0xffffffff；L128分支数等指标与L64一致.

3.3 抗攻击安全

3.3.1 差分攻击

采用截断差分的思想分析SMBA算法抵抗差分攻击的能力.Mouha[5]给出了一种采用混合整数规划模型搜索差分活动S盒的方法,我们结合S0和S1的差分概率权重,分别评估SMBA-128和SMBA-256具有的最大差分特征概率.SMBA-128经过13轮迭代后最大差分特征概率不大于2-129.96,小于安全界2-128；SMBA-256经过18轮迭代后最大差分特征概率不大于2-264.600,小于安全界2-256.最大差分特征概率搜索结果详见表3、表4.

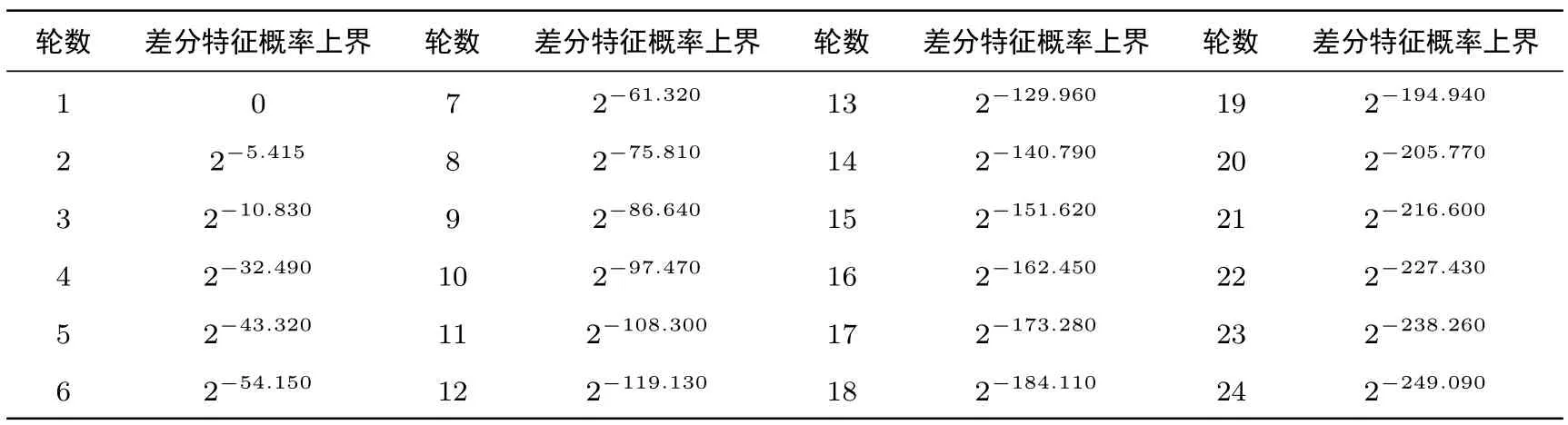
表3 SMBA-128差分概率Table 3 Differential probability of SMBA-128

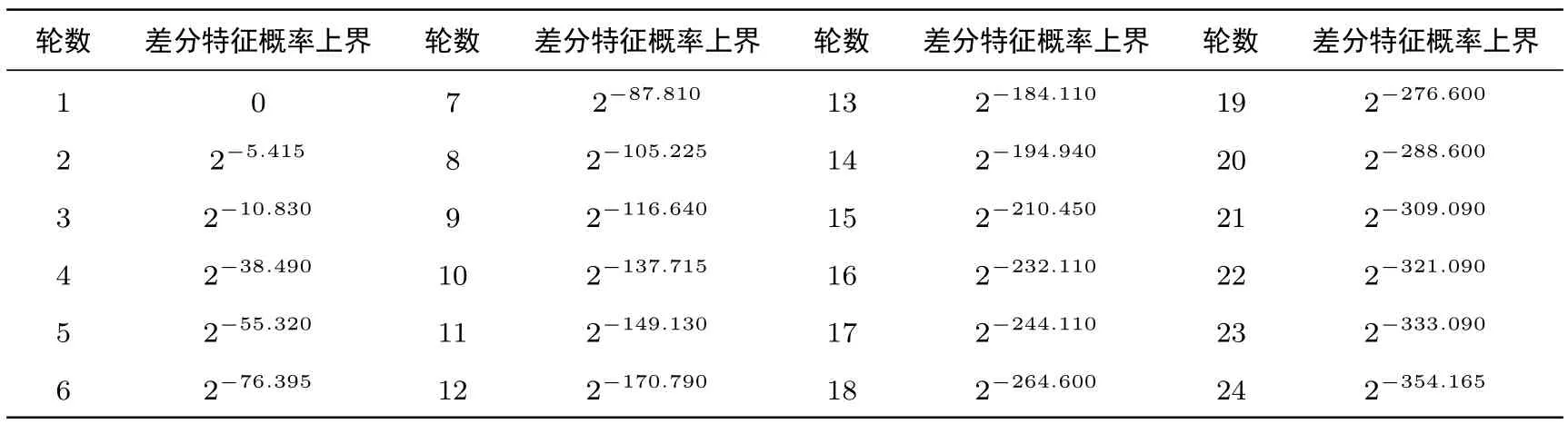
表4 SMBA-256差分概率Table 4 Differential probability of SMBA-256

3.3.2 线性攻击

与差分攻击方法相似可得,SMBA-128经过13轮迭代后最大线性特征概率不大于2-128.544,小于安全界2-128；SMBA-256经过18轮迭代后最大线性特征概率不大于2-262.240,小于安全界2-256.最大线性特征概率搜索结果详见表5、表6.

3.3.3 代数攻击

SMBA算法的S0不存在二次关系,S1存在39个二次关系,可构造的二次方程数量低于AES,涉及的变量数不低于AES,使用XL算法求解构造的二次方程组求解复杂度应高于AES,可认为SMBA能够抵抗代数攻击.

3.3.4 积分攻击

对于128比特分组的SMBA-128算法,令算法输入的多重集合具有可除性则经7轮加密后输出的多重集合的第9到第16个字节为平衡字节,而经8轮加密后输出的多重集合的每个字节都是不确定字节,即算法存在7轮积分区分器.对于256比特分组的SMBA-256算法,令算法输入的多重集合具有可除性则经8轮加密后输出的多重集合的第17到第32个字节为平衡字节,而经9轮加密后输出的多重集合的每个字节都是不确定字节,即算法存在8轮积分区分器.

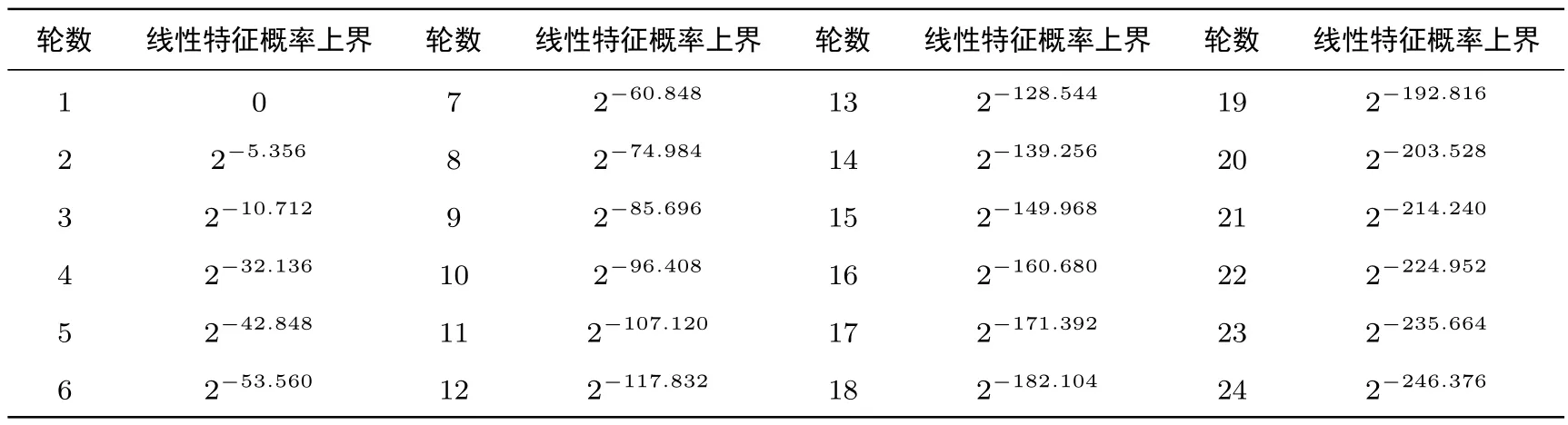
表5 SMBA-128线性概率Table 5 Linear probability of SMBA-128

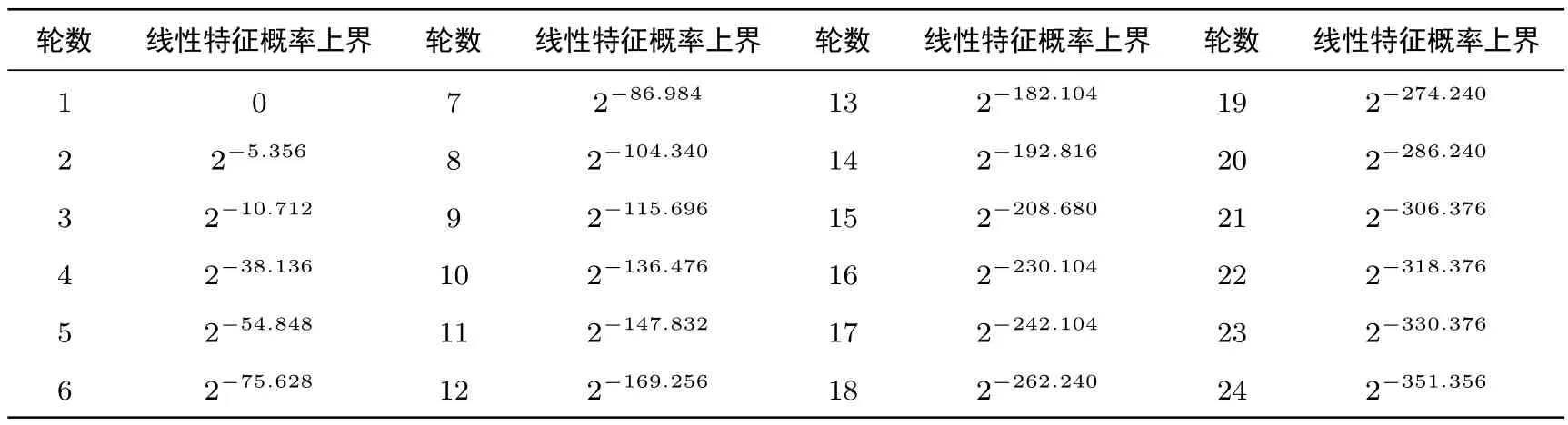
表6 SMBA-256线性概率Table 6 Linear probability of SMBA-256

3.3.5 不可能差分攻击

利用文献[6]中的方法,对SMBA-128可找到5轮不可能差分,与Feistel结构天然具有的不可能差分一致.对SMBA-256找到了17 786条8轮不可能差分,如下即为一条8轮不可能差分.

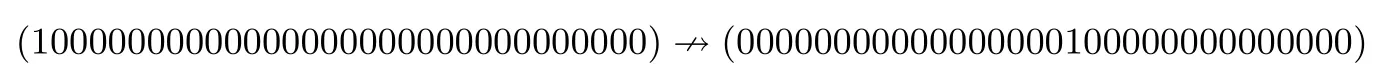
3.3.6 相关密钥差分攻击

采用截断差分的思想分析SMBA算法抵抗相关密钥差分攻击的能力,可得9轮SMBA-128-128的相关密钥差分特征概率不大于2-133.470,小于安全界2-128；21轮SMBA-128-256的相关密钥差分特征概率不大于2-259.620,小于安全界2-256；12轮最大SMBA-256-256相关密钥差分特征概率为2-304.11,小于安全界2-256.相关密钥差分特征概率搜索结果详见表7、表8、表9.

表7 SMBA-128-128相关密钥差分概率Table 7 Related-key differential probability of SMBA-128-128

3.3.7 飞去来器攻击

9轮SMBA-128算法任意分成两段至少具有12个差分活动S盒,飞去来器攻击成功的概率不大于2-5.415×12×2=2-129.96＜2-128；13轮SMBA-256算法任意分成两段至少具有27个差分活动S盒,飞去来器攻击成功的概率不大于2-5.415×27×2=2-292.41＜2-256.因此,可认为SMBA算法能抵抗飞去来器攻击.

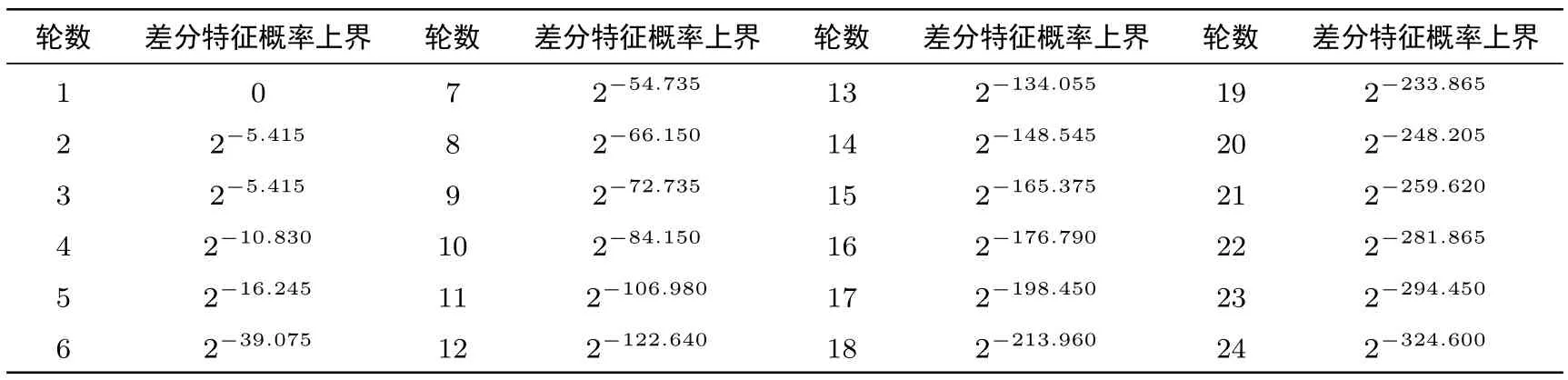
表8 SMBA-128-256相关密钥差分概率Table 8 Related-key differential probability of SMBA-128-256

表9 SMBA-256-256相关密钥差分概率Table 9 Related-key differential probability of SMBA-256-256

3.3.8 滑动攻击

由于SMBA密钥扩展算法的设计,可证明SMBA-128-128和SMBA-256-256对相同密钥或是两个不同密钥,不会有任意连续3轮子密钥均相同；对SMBA-128-256,对相同密钥或是两个不同密钥,不会有连续5轮子密钥相同.因此我们认为SMBA可以抵抗滑动攻击.

3.3.9 密钥扩展安全性

SMBA的密钥扩展算法具有保熵性.通过仔细的分析,我们认为SMBA不具有等价密钥、弱密钥或半弱密钥.

3.4 侧信道攻击安全防护

SMBA算法的2个S盒都采用代数构造的方式设计,具有较好的透明阶、改进的透明阶、Hamming重量的混乱系数方差等指标,使得在相同安全防护条件下,抵抗侧信道攻击的能力更强.另外,S盒掩码防护实现难度(芯片面积占用、随机数使用量等)和S盒逻辑表达式的乘法复杂度密切相关,逻辑复杂度越低,安全防护实现时使用的随机数量越少、芯片占用面积越低,因此,在S0和S1构造过程中本算法尽量使用乘法复杂度低的部件、运算,使得S0和S1的乘法复杂度低.

4 性能分析

4.1 软件性能

算法的软件性能测试标准是在CBC模式下,用256字节数据作为输入进行性能测试,每次测试变换密钥,取105次CBC模式运算测试结果的平均值作为速率测试的结果.

32比特ARM环境采用基于STM32 F103的开发板(主频72 Mhz):stm32f1zet6核心板6、512 K片内Flash、64 K片内RAM.算法采用查表方式实现,实现结果见表10.

表10 32比特ARM环境下SMBA算法性能Table 10 Performance of SMBA on 32-bit ARM platform

SMBA的64位软件实现平台采用Intel Core(TM)i7-9750H CPU、主频2.6 GHz、Windows10、内存32 G、Microsoft Visual Studio 2017编译器.算法加密过程采用查表方式实现,解密过程使用AVX指令实现,实现结果见表11.

表11 64比特Windows环境下SMBA算法性能Table 11 Performance of SMBA on 64-bit Windows platform

4.2 硬件性能

算法的ASIC实现环境,采用的设计库为HJTC0.11 um工艺库,采用的综合工具为Synopsys Design Vision(F-2011.09-SP1 Version).仿真环境为Modelsim SE 10.1a.算法测试32个分组长度数据,测试结果见表12.

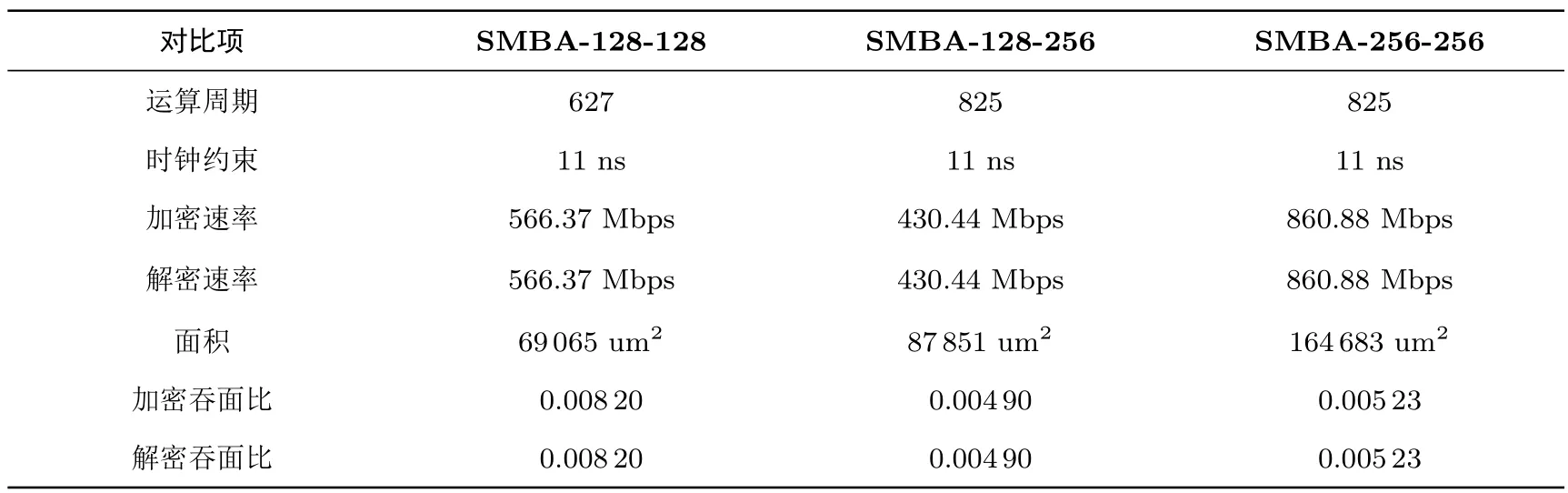
表12 ASIC环境下SMBA算法性能Table 12 Performance of SMBA on ASIC

5 优缺点分析

SMBA是安全性高、实用性强、创新设计的分组密码算法,算法的设计具备简洁性、灵活性和兼容性,完全能够满足本次算法设计竞赛的要求.

5.1 算法特色

(1)算法设计简洁,三个版本共用非线性变换S0和S1,以及线性变换L64,扩展自然.

(2)算法适用于多种软件平台,如8/32/64位平台,且算法的软件性能高,实用性强.

(3)算法安全性分析充分,安全界清晰,具有较高的安全冗余.

(4)算法具有良好的抵抗侧信道攻击的能力.由于我们在S0和S1的设计中充分考虑到了侧信道防护的问题,S0和S1在透明阶、DPA信噪比、Hamming重量混乱系数方差等评价侧信道防护能力的指标上都优于AES的S盒.在S0和S1构造过程中本算法尽量使用乘法复杂度低的部件、运算,使得S0和S1的乘法复杂度低.由于针对线性变换的侧信道防护策略是平凡的,所以我们认为SMBA具有良好的抗侧信道攻击能力.

5.2 创新点

(1)创新设计了密码性质优、软硬件实现性能高的线性变换L64:与同等规模的MDS变换相比,L64的实现代价非常小,其只由两个简单的L32变换和一个L-M结构线性变换构成,软硬件实现简单,但同时其分支数可达到6,且能够将1个非零字节变换为7个非零字节,具有良好的密码学性质.利用L64的密码性质,通过理论证明和计算机搜索(两者结果相同)均可证明,SMBA-128具有很高的抵抗差分攻击和线性攻击的能力.

(2)SMBA-256整体设计保证安全:换位变换P128结合两个并置的线性变换L64,确保SMBA-256的加解密过程都形成一个整体,大幅度提升密码算法的扩散性和抗攻击能力.

(3)面向实现优化设计:设计了密码指标高的S盒S0和S1,尤其是S0的设计.与已有主要密码指标相同的S盒相比,硬件实现电路的门数和深度均有减少.

5.3 不足

由于设计中采用了8比特S盒,且分组长度/密钥长度大,因此SMBA算法不适用于低功耗和硬件资源受限的轻量级应用环境.

附录

SMBA-128-128测试向量:

密钥:0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00.

明文:0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00.

密文:0x21,0x9a,0x3b,0x8f,0x61,0x47,0x98,0x64,0x8f,0xc4,0xd6,0xd1,0x9d,0x72,0x86,0x6d.

SMBA-128-256测试向量:

密钥:0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00.

明文:0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00.

密文:0x40,0x76,0x91,0x2d,0xfc,0x2b,0x9b,0xe2,0x20,0xb9,0x76,0x27,0xe1,0x72,0xf3,0x33.

SMBA-256-256测试向量:

密钥:0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00.

明文:0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00.

密文:0x1b,0x8b,0x33,0x77,0x1d,0x34,0xa3,0x64,0xd2,0x89,0x20,0x99,0xb3,0xd9,0x0b,0x1f,0x43,0x62,0x50,0xea,0x73,0x6c,0x45,0x30,0xa3,0xd3,0xf8,0xa4,0xab,0x1c,0xb7,0x59.