Raindrop:面向硬件设计的分组密码算法*

李永清,李木舟,2,付勇,2,樊燕红,2,黄鲁宁,2,王美琴,2

1.密码技术和信息安全教育部重点实验室,青岛266237

2.山东大学网络空间安全学院,青岛266237

1 引言

密码技术是保障信息安全的核心技术,密码算法和密码产品能够自主可控是保证我国信息安全的重要条件.密码算法是保障信息安全的核心工具和基础支撑,是解决信息安全问题最有效、最可靠、最经济的手段.分组密码算法是密码算法中的一个核心分支,其主要作用是保证信息的机密性和完整性,在通信系统中起到重要作用.分组密码算法是将一个明文分组作为整体加密,并且通常得到的是与明文等长的密文分组,两个用户之间要共享一个对称加密密钥.1977年,DES[1]被美国国家标准局采纳为联邦信息处理标准.2001年,美国国家标准技术研究所发布了高级加密标准AES[2],并成为当今主流分组加密算法.随着人们对分组密码算法的研究更加深入,越来越多的分组加密算法被提出,例如Midori算法[3]、Simon算法[4]、SPECK算法[4]等等.分组密码算法的结构主要有三种:Feistel结构、SPN结构和Lai-Massey结构,不同的结构具有不同的特点,因此结构的选取也是设计分组密码算法时首先需要考虑的问题之一.随着人们对分组密码算法的要求越来越高,发展方向逐渐偏向轻量级分组密码算法,例如2016年提出的SKINNY算法[5]、2017年提出的GIFT算法[6]等等.

Raindrop算法采用Feistel结构,使得加解密一致,采取较为简单轮函数,降低算法硬件实现代价,同时保证算法的安全性,旨在设计一个轻量级分组密码算法.

1.1 主要贡献

本文给出了一个面向硬件设计的分组加密算法——Raindrop算法.该算法共三个版本:Raindrop-128/128/60、Raindrop-128/256/80和Raindrop-256/256/100(其中Raindrop-n/k/R:n为分组长度,k为密钥长度,R为总轮数).Raindrop算法主要具有以下几个特点:

(1)加解密一致,节省资源Raindrop算法采用Feistel结构,加密过程中,两部分消息状态进行交换,在最后一轮不交换,使得加密过程与解密过程一致,能够节省较多的硬件资源,不需要为解密算法付出额外代价.

(2)轮函数简单,易于轻量化实现在Raindrop算法的非线性运算中,每个输出比特只需通过1个与运算、1个非运算和1个异或运算便可得到,且线性层的二元域矩阵深度为1,因此易于轻量化实现.

(3)安全性较强我们利用自动化搜索工具STP对Raindrop算法进行评估,主要包括差分分析[7]、线性分析[8]、不可能差分分析[9]等.评估结果表明,Raindrop算法足够抵抗目前已知的攻击.

1.2 本文框架

本文之后内容安排如下:第2节给出Raindrop算法描述；第3节给出Raindrop算法伪代码；第4节给出Raindrop算法设计原理；第5节和第6节分别给出Raindrop算法的安全性分析和软硬件性能.最后第7节总结全文.

2 Raindrop算法描述

在描述算法之前,如下定义本文档中使用的表示符号:

Raindrop-n/k/R:分组长度/密钥长度/算法总轮数的Raindrop算法版本

Raindrop-n/k:分组长度为n,密钥长度为k的Raindrop算法版本

K: 主密钥 Kr: 第r轮轮密钥,r≥1

RF64: 输入为64比特的轮函数 RF128: 输入为128比特的轮函数

Si: 输入为i比特的S盒 M: 行混合操作

⊕: 异或操作

2.1 Raind rop算法参数

Raindrop算法共三个版本:Raindrop-128/128、Raindrop-128/256和Raindrop-256/256,每个版本的参数如表1所示.

2.2 算法结构

Raindrop算法整体采用Feistel结构,轮函数采用SP结构,包含S盒代换、行混合、列循环移位操作.为了保证加解密的一致性,最后一轮不进行状态的交换,轮函数和加密算法的结构见图1.

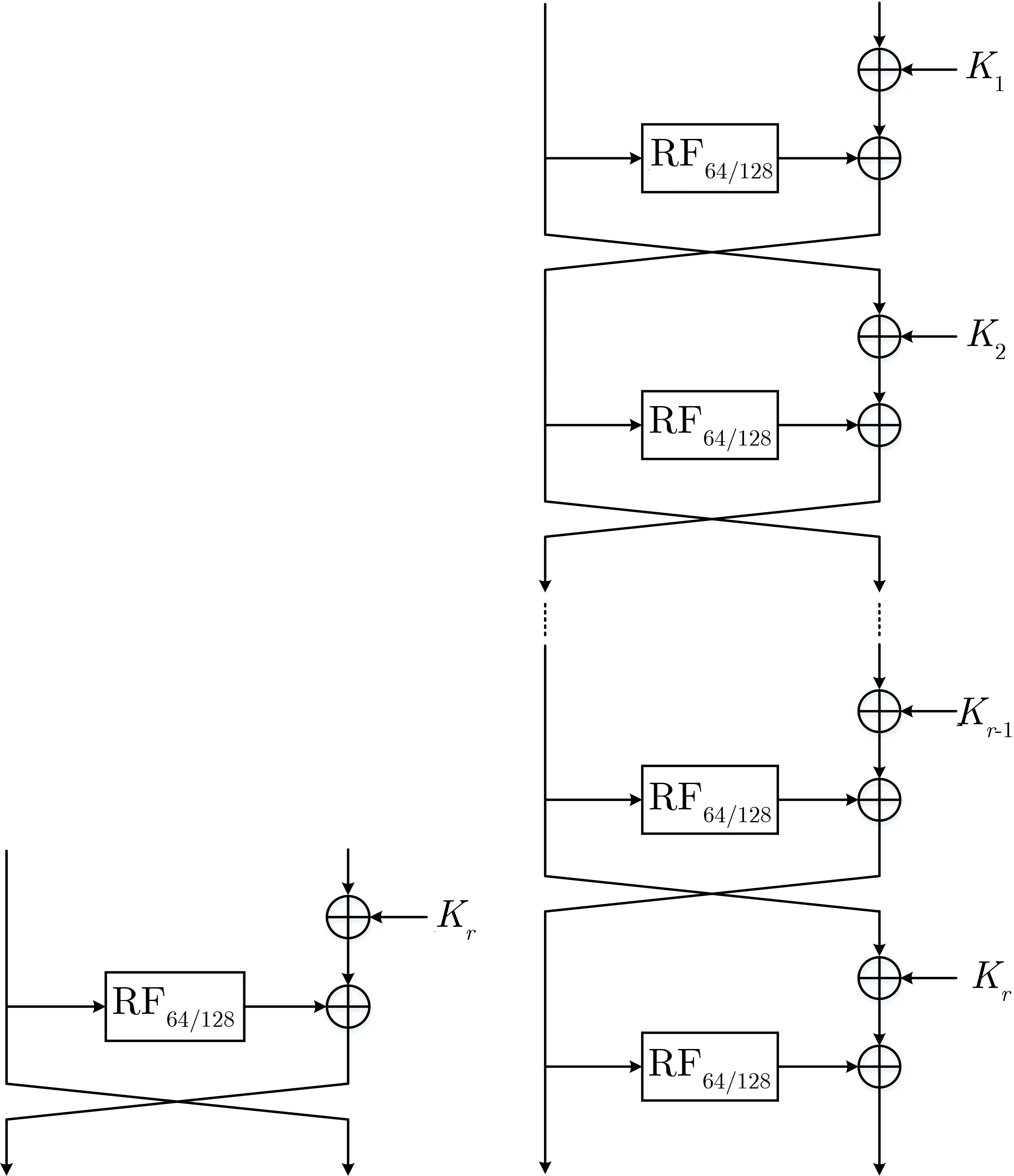
图1 Raindrop算法的轮函数和整体结构Figure 1 Round function and whole construction of Raindrop

2.2.1 消息状态排列

Raindrop算法采用Feistel结构,包括两部分消息状态.轮函数的输入可以用一个4×4的二维矩阵表示,称其为状态矩阵.

若轮函数的输入为64比特,表示为p0p1···p15,可以将其按照如下顺序映射成4×4的状态矩阵:

其中pi的长度|pi|满足:当i=0,4,8,12,2,6,10,14时,有|pi|=3；其余情况下,有|pi|=5.

若轮函数的输入为128比特时,可以用相同的二维矩阵来表示输入状态,pi的长度|pi|满足:当i=0,4,8,12,2,6,10,14时,有|pi|=7；其余情况下,有|pi|=9.

每一个pi在本文中被称为一个word,因此消息状态可以看成16个word的组合.

2.2.2 S盒代换

S盒代换操作使用不同大小的S盒.其中Raindrop-128/128、Raindrop-128/256采用3比特和5比特S盒,Raindrop-256/256采用7比特和9比特S盒.S盒的构造使用了Keccak函数[10]中非线性运算的布尔表达式.假设k比特S盒的输入为(xk-1,xk-2,···,x1,x0),输出为(yk-1,yk-2,···,y1,y0),则输出比特和输入比特满足如下关系:

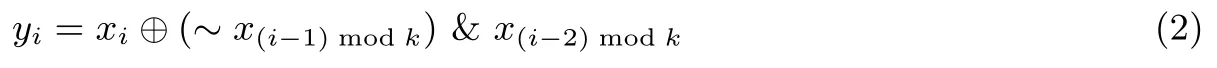
2.2.3 行混合

行混合矩阵为:

此矩阵右乘状态矩阵,可以得到行混合之后的值,即:

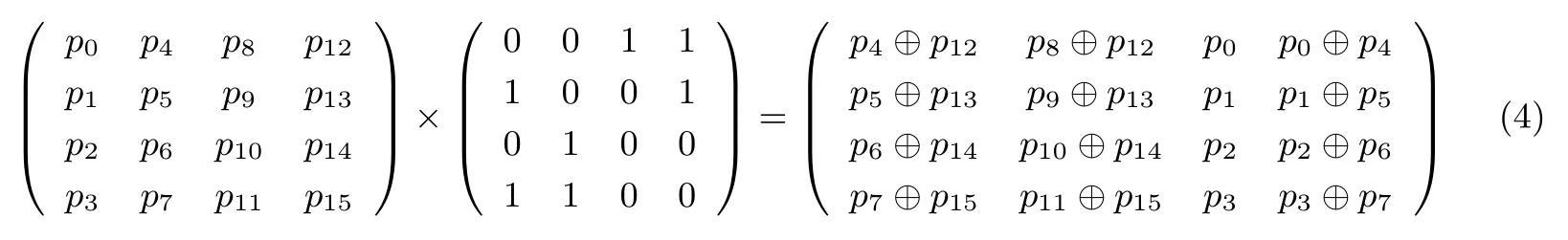
2.2.4 列循环移位

记状态矩阵的第i列的级联值为Coli=p4i||p(4i+1)||p(4i+2)||p(4i+3),其中0≤i≤3.

对Raindrop-128/128、Raindrop-128/256算法,每一列按照下述方式进行比特级的循环移位,即:Col0不变,Col1向左循环6比特,Col2向左循环7比特,Col3向左循环12比特.

对Raindrop-256/256算法,每一列按照下述方式进行比特级的循环移位,即:Col0不变,Col1向左循环12比特,Col2向左循环14比特,Col3向左循环24比特.

2.3 密钥生成算法

Raindrop算法采用线性操作生成每轮的轮密钥.Raindrop-128/128主密钥为128比特,每轮异或64比特轮密钥,Raindrop-128/256主密钥为256比特,每轮异或64比特轮密钥,Raindrop-256/256主密钥为256比特,每轮异或128比特轮密钥.

2.3.1 Raindrop-128/128密钥生成算法

假设我们需要生成R轮的轮密钥,那么首先将128比特的主密钥赋给密钥状态TK1,然后按照图2所示的方式依次生成密钥状态TKr,其中r代表轮数,满足2≤r≤R,(r-1)||0···0是密钥生成算法中使用的轮常数,0···0代表64比特的“0”,即轮常数异或在上,A4代表执行连续的4次A函数.在执行A函数时,将128比特的密钥状态分成8块,每块16比特,即函数具体的形式见图3,注意函数的最后一步是对这128比特的状态进行一个整体的左循环移5位的操作.第r轮的64比特轮密钥Kr是TKr的第64至127比特,即Kr=TKr[127:64].

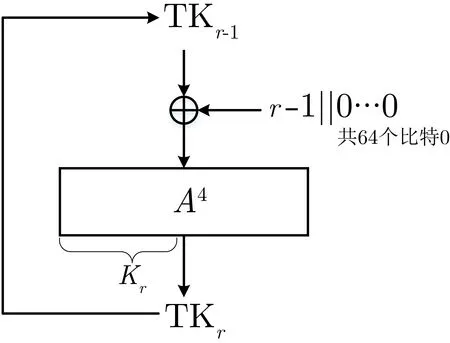
图2 Raindrop-128/128的密钥生成算法Figure 2 KeyGeneration of Raindrop-128/128

2.3.2 Raindrop-128/256密钥生成算法

Raindrop-128/256算法的密钥生成算法的整体结构与Raindrop-128/128类似,首先将256比特的主密钥赋给密钥状态TK1,然后按照图4所示的方式依次生成密钥状态TKr,其中r代表轮数,满足2≤r≤R,(r-1)||0···0是密钥生成算法中使用的轮常数,0···0代表160比特的“0”,即轮常数异或在代表执行连续的4次B函数.在执行B函数时,将256比特的密钥状态分成8块,每块32比特,即函数具体的形式见图5,注意函数的最后一步是对这256比特的状态进行一个整体的左循环移13位的操作.第r轮的64比特轮密钥Kr是TKr的第240至255比特,第208至223比特,第176至191比特,第144至159比特的级联值,即:Kr=TKr[255:240]||TKr[223:208]||TKr[191:176]||TKr[159:144].

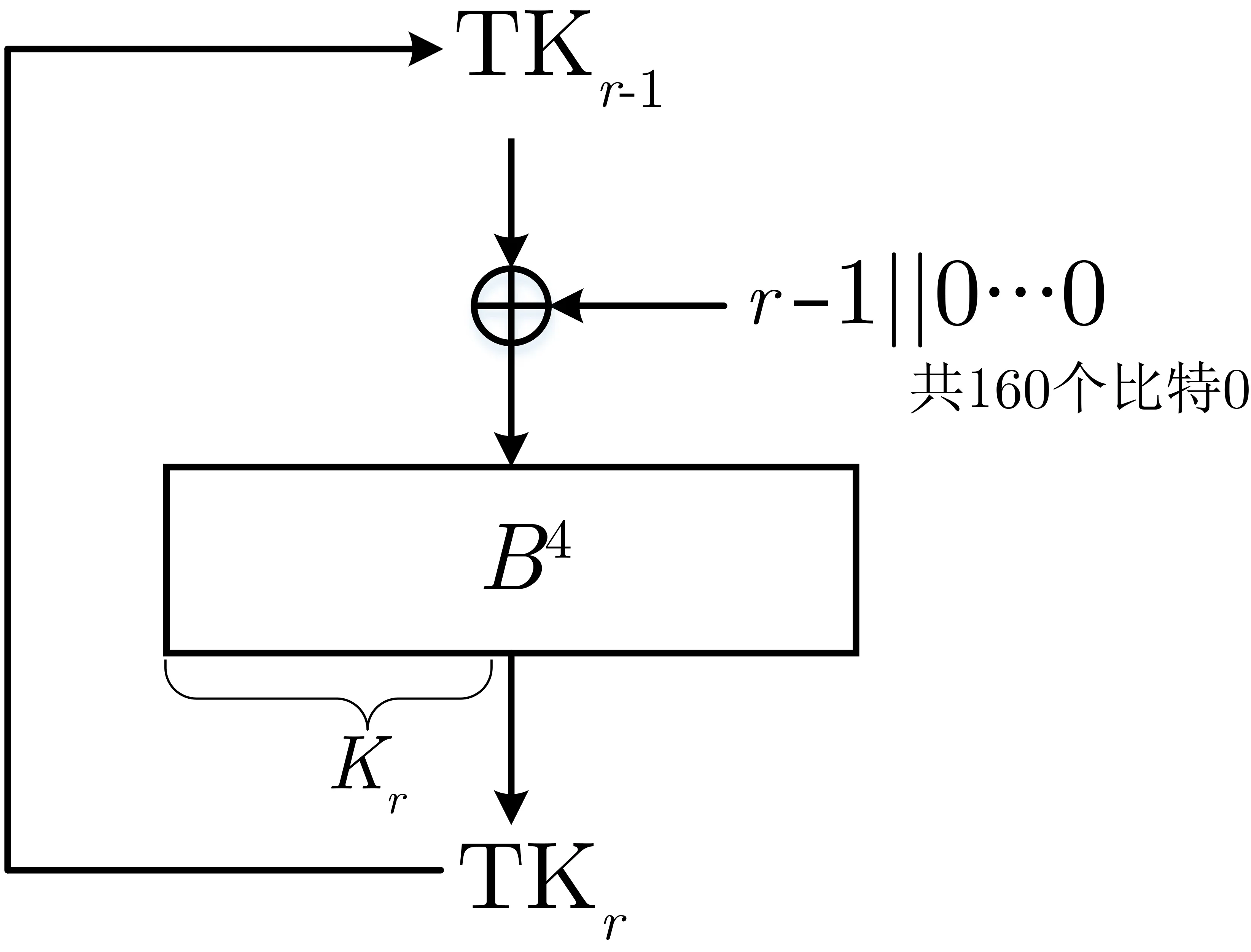
图4 Raindrop-128/256的密钥生成算法Figure 4 KeyGeneration of Raindrop-128/256

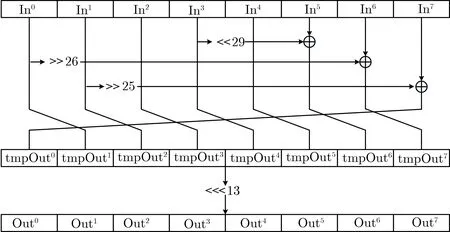
图5 B函数Figure 5 Function B

2.3.3 Raindrop-256/256密钥生成算法

Raindrop-256/256的密钥生成算法与Raindrop-128/256算法的密钥生成算法相同,只不过Raindrop-256/256使用128比特的轮密钥.第r轮的128比特轮密钥Kr是TKr的第128至255比特,即:Kr=TKr[255:128].

3 算法伪代码

3.1 加密算法

假设输入的明文为PL||PR,第r轮的轮密钥为Kr,加密轮数为R,输出的密文为CL||CR,S盒代换操作为S,行混合操作为M,列循环移位操作为BR,则加密算法如算法1.

算法1加密算法In p ut:input parameters P L||P R,Kr,R Outp ut:output C L||C R 1 P L0||P0R=P L||P R；2 for 0≤r＜R-1 d o 3 P L=P L；r+1 r 5 en d r+1=(PrR⊕Kr+1)⊕(BR◦M◦S(PrL))；4 P R 6 C L=PRL-1；7 C R=(P R R-1⊕KR)⊕(BR◦M◦S(PRL-1))；

3.2 S盒代换

假设S盒的输入为PL,输入大小为n比特,输出为S(PL),Si为i比特S盒,则S盒代换操作算法如算法2.

3.3 行混合

行混合为二元域矩阵右乘状态矩阵,假设行混合的输入为P,行混合的输出为M(P),则行混合算法如算法3.

3.4 列循环移位

列循环移位是状态矩阵的每一列进行循环移位,假设输入为P,输入大小为n比特,输出为BR(P),则列循环移位算法如算法4.

算法3行混合Inp ut:P Outp ut:M(P)1 p0||p1||···||p1 5=P排列方式如公式(1)；2 for i=0,1,2,3 d o 3 Ti=pi+4⊕pi+1 2；4 end 5 for i=4,5,6,7 d o 6 Ti=pi+4⊕pi+8；7 end 8 for i=8,9,10,11 d o 9 Ti=pi-8；1 0 end 1 1 for i=12,13,14,15 d o 1 2 Ti=pi-1 2⊕pi-8；1 3 end 1 4 M(P)=T0||T1||···||T1 5算法4列循环移位Inp ut:P Outp ut:BR(P)1 p0||p1||···||p1 5=P排列方式如公式(1)；2 if n=64 then 3 T0=p0||p1||p2||p3；4 T1=(p4||p5||p6||p7)⋘6；5 T2=(p8||p9||p1 0||p1 1)⋘7；6 T3=(p1 2||p1 3||p1 4||p1 5)⋘12；7 end 8 if n=128 then 9 T0=p0||p1||p2||p3；10 T1=(p4||p5||p6||p7)⋘12；11 T2=(p8||p9||p10||p11)⋘14；12 T3=(p12||p13||p14||p15)⋘24；13 en d 14 BR(P)=T0||T1||T2||T3；

3.5 Raind rop-128/128密钥生成算法

设Raindrop-128/128轮数为R,主密钥为K,第r轮的轮密钥为Kr,A函数为A,则Raindrop-128/128的密钥生成算法如算法5.

算法5 Raindrop-128/128密钥生成算法Inp ut:K,R Ou tp ut:Kr 1 TK 1=K；2 for 2≤r≤R d o 3 TK r=A◦A◦A◦A(TK r-1⊕((r-1)||000···000)),(r-1)共级联了64个0 4 en d 5 for 1≤r≤R d o 6 Kr=TK r[127:64]；7 en d

3.6 Raind rop-128/256密钥生成算法

设Raindrop-128/256轮数为R,主密钥为K,第r轮的轮密钥为Kr,B函数为B,则Raindrop-128/256的密钥生成算法如算法6.

算法6 Raindrop-128/256密钥生成算法Inp ut:K,R Ou tp ut:Kr 1 TK 1=K；2 for 2≤r≤R d o 3 TK r=B◦B◦B◦B(TK r-1⊕((r-1)||000···000)),(r-1)共级联了160个0 4 en d 5 for 1≤r≤R d o 6 Kr=TK r[255:240]||TK r[223:208]||TK r[191:176]||TK r[159:144]；7 en d

3.7 Raind rop-256/256密钥生成算法

设Raindrop-256/256轮数为R,主密钥为K,第r轮的轮密钥为Kr,B函数为B,则Raindrop-256/256的密钥生成算法见算法7.

算法7 Raindrop-256/256密钥生成算法In p ut:K,R Outp ut:Kr 1 TK 1=K；2 for 2≤r≤R d o 3 TK r=B◦B◦B◦B(TK r-1⊕((r-1)||000···000)),(r-1)共级联了160个0 4 en d 5 for 1≤r≤R d o 6 Kr=TK r[255:128]；7 en d

3.8 A函数

A函数用于Raindrop-128/128密钥生成算法中,设输入为PK,输出为TK,则A函数的算法见算法8.

算法8 A函数Inp ut:PK Outp ut:TK 1 In0||In1||In2||In3||In4||In5||In6||In7=PK；2 tmp Out0=In7⊕(In0≫10)；3 tmp Out1=In0；4 tmp Out2=In1；5 tmp Out3=In2；6 tmp Out4=In3；7 tmp Out5=In4；8 tmp Out6=In5⊕(In2≫15)；9 tmp Out7=In6⊕(In1≫15)；10 TK=(tmp Out0||tmp Out1||tmp Out2||tmp Out3||tmp Out4||tmp Out5||tmp Out6||tmp Out7)⋘5；

3.9 B函数

B函数用于Raindrop-128/256和Raindrop-256/256密钥生成算法中,设输入为PK,输出为TK,则B函数的算法见算法9.

算法9 B函数In p ut:PK Outp ut:TK 1 In0||In1||In2||In3||In4||In5||In6||In7=PK；2 tmp Out0=In7⊕(In1≫25)；3 tmp Out1=In0；4 tmp Out2=In1；5 tmp Out3=In2；6 tmp Out4=In3；7 tmp Out5=In4；8 tmp Out6=In5⊕(In3≪29)；9 tmp Out7=In6⊕(In0≫26)；10 TK=(tmp Out0||tmp Out1||tmp Out2||tmp Out3||tmp Out4||tmp Out5||tmp Out6||tmp Out7)⋘13；

4 设计原理

在设计Raindrop算法时,主要考虑了硬件实现代价.设计原理是采用较为简单的非线性层和线性层,减少硬件面积,降低关键路径上的时延.构造异或数较少的线性密钥生成算法,同时保证密钥生成算法扩散速度较快.

4.1 简单非线性函数

我们通过Keccak非线性运算的布尔表达式来生成Raindrop的4种S盒,该布尔表达式只包含1个与操作,1个非操作,1个异或操作,满足硬件面积小,时延短的要求.

4.2 简单线性层

我们选取一个深度为1的二元域矩阵作为线性层的一部分,深度为1保证了在关键路径上最多只贡献1个异或,同时整个矩阵总的异或数较少,也满足了我们对硬件实现的要求.

4.3 线性密钥生成算法

对于Raindrop-128/128算法生成1轮轮密钥总共只需要32个异或,对于Raindrop-128/256和Raindrop-256/256算法,生成1轮轮密钥只需要64个异或,同时通过筛选密钥生成算法中的移位数、异或位置和循环移位数来达到较好的扩散性.

5 安全性分析

本节给出Raindrop算法的差分分析、线性分析、不可能差分分析、零相关分析和积分分析的结果.鉴于算法结构本身特点,其它分析方法(如中间相遇攻击等)对算法安全性的影响较小,本文不再给出分析结果.

5.1 差分分析

利用STP搜索工具建立自动化搜索模型,我们发现Raindrop-128/128、Raindrop-128/256和Raindrop-256/256算法16轮最小活跃S盒个数均大于等于32.根据S盒的差分分布表,我们可知3比特、5比特、7比特、9比特S盒的非0差分传播概率的最大值均为2-2,因此Raindrop-128/128和Raindrop-128/256算法不存在32轮及更长轮数的有效差分路线,Raindrop-256/256算法不存在64轮及更长轮数的有效差分路线.因此Raindrop算法能够抵抗差分攻击的.

5.2 线性分析

利用STP搜索工具建立自动化搜索模型,我们发现Raindrop-128/128、Raindrop-128/256和Raindrop-256/256算法16轮最小活跃S盒个数均大于等于32.根据S盒的线性近似表,我们可知3比特、5比特、7比特、9比特S盒的非0掩码传播相关性的最大值均为2-1.因此Raindrop-128/128和Raindrop-128/256算法不存在32轮及更长轮数的有效线性路线,Raindrop-256/256算法不存在64轮及更长轮数的有效线性路线.因此Raindrop算法能够抵抗线性攻击的.

5.3 不可能差分分析

利用STP搜索工具建立自动化搜索模型,我们要求输入差分只有1个pi(一个word)活跃,输出差分只有1个pi(一个word)活跃.在这种情况下,Raindrop算法均不存在13轮及以上的1-1 word不可能差分.因此,Raindrop算法是抵抗1-1 word不可能差分攻击的.

5.4 零相关分析

利用STP搜索工具建立的自动化搜索模型,在限定输入掩码和输出掩码各只有一个pi(一个word)活跃的前提下,Raindrop算法均不存在13轮及以上的1-1 word零相关路线.因此,Raindrop算法是抵抗1-1 word零相关攻击的.

5.5 积分攻击

利用STP搜索工具建立的自动化搜索模型,使用比特级的Division Property对Raindrop算法进行分析,Raindrop-128/128和Raindrop-128/256算法的积分区分器最长为7轮,Raindrop-256/256积分区分器最长为13轮.因此Raindrop算法是抵抗积分攻击的.

6 Raindrop性能分析

6.1 软件性能分析

本节给出Raindrop算法在64 bit Windows环境和32 bit ARM环境下的实现结果.测试环境分别为:Intel(R)Core(TM)i7-6700T CPU 2.40 GHz主频、64位Windows10操作系统、16 GB内存,X86-64环境和基于STM32 F103的开发板(主频72 Mhz):stm32f1zet6核心板6、512 K片内Flash、64 K片内RAM.

在进行性能测试时,采用256字节数据作为输入,每次测试变换密钥,取105次CBC模式运算测试结果的平均值为加/解密速率的结果,其中加/解密执行时间包含密钥扩展算法运算时间.测试结果见表2.由于CBC模式下的解密过程可以并行实现,我们在表中给出的解密速率是基于多路实现结果.其中

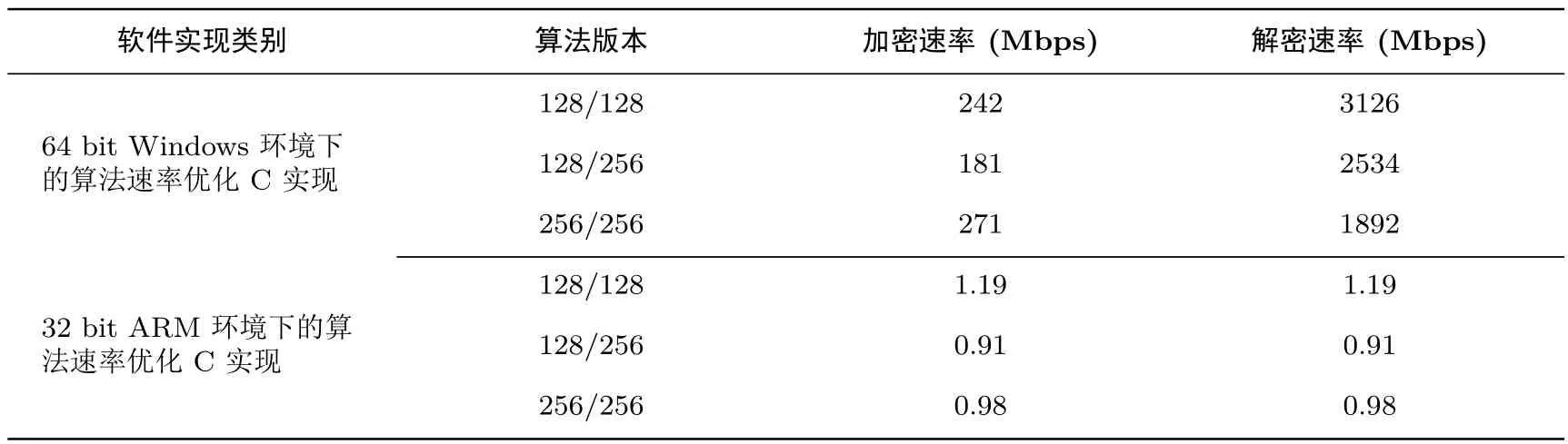
表2 软件实现结果Table 2 Results of software implementation

6.2 硬件性能分析

本节给出Raindrop算法的Verilog硬件仿真实现结果.采用的仿真工具为ModelSim SE 10.1a,综合工具为Synopsys Design Vision(F-2011.09-SP1 Version),以及工艺库为HJTC 0.11 um.算法Verilog硬件仿真实现采用32个分组数据进行加/解密.算法实现的加/解密运算用时包含密钥扩展运算用时.算法电路面积规模为包含加密、解密、密钥扩展运算的算法整体实现的含互连线面积.

具体方法如下:

(1)仿真验证

使用ModelSim对算法实现正确性进行仿真验证,并记录32个分组数据运算(含密钥扩展运算)占用的时钟周期数.

(2)性能自测试

在给定的时钟约束条件上进行前端综合,得到并记录以下测试数据:

1)关键路径时长

在Synopsys Design Complier中进行关键路径时长测试.根据算法设计提供的自测数据,设置相应的时钟约束条件,通过综合软件得到关键路径时长.

2)速率

在关键路径时长合理的条件下,通过以下公式计算加解密速率:

加密速率=加密数据长度/(时钟约束条件×加密占用的时钟周期数)

解密速率=解密数据长度/(时钟约束条件×解密占用的时钟周期数)

3)面积

在可满足的最小时钟约束条件下,在HJTC 0.11 um工艺库基础上进行综合,记录算法实现面积(包含加密、解密、密钥扩展运算的算法整体实现的含互连线面积).

4)吞面比

加密吞面比=加密速率/算法电路面积

解密吞面比=解密速率/算法电路面积

实现结果如表3所示.

表3 Verilog硬件仿真实现结果Table 3 Results of Verilog harware simulation implementation

7 总结

本文给出了一个新的分组加密算法——Raindrop算法.Raindrop算法采用Feistel结构.轮函数为SP结构,采用不同大小S盒进行组合,S盒的布尔表达式只包含1个与操作、1个非操作、1个异或操作.轮函数的行混合操作使用深度为1的二元域矩阵.密钥生成算法使用异或数较少,扩散性较强的线性操作.通过以上特点可以看出,轮函数容易进行门限实现,且实现代价很小,从而保证了Raindrop算法在硬件实现上具有较好的优势.此外,本文通过利用自动化搜索工具STP对Raindrop算法的安全性进行评估,评估结果显示Raindrop算法可以抵抗差分攻击、线性攻击等已知攻击,具有较好的安全冗余.

但由于Raindrop算法采用了3、5、7、9比特S盒,使得软件实现较为繁琐,同时由于Raindrop算法的独特性,在安全性分析时,主要对活跃S盒的个数进行评估,最终使得Raindrop算法的安全界较为宽松,因此降低Raindrop算法的轮数仍有很大潜力.