轻量级分组密码算法FBC*
冯秀涛,曾祥勇,张凡,曾光,唐灯,甘国华,王永兴,8
1.中国科学院数学与系统科学研究院,中国科学院数学机械化重点实验室,北京100190
2.湖北大学数学与统计学学院,应用数学湖北省重点实验室,武汉430062
3.兴唐通信科技有限公司,北京100191
4.战略支援部队信息工程大学网络空间安全学院数学工程与先进计算国家重点实验室,郑州450001
5.西南交通大学数学学院,成都610031
6.北京太一云科技有限公司,北京100125
7.北京科技大学计算机与通信工程学院,北京100083
8.中国科学院大学数学学院,北京100049
1 概述
分组密码是一种典型的对称密码算法,它采用固定的密码函数,在密钥的控制下对输入的明文消息进行加密得到密文消息,或者对密文消息进行解密得到明文消息.典型的分组密码算法包括美国早期的数据加密标准DES、现行的高级加密标准AES、我国的商业密码行业标准SM4[1]等.分组密码结合密码模式已被广泛用在安全存储、网络通信加密中.
轻量级分组密码是一种特殊的分组密码体制,其主要是指密码算法硬件实现和运行时所占用的系统资源的开销较少,例如硬件实现面积、运行时所占内存空间大小和能耗等.这类分组密码算法主要被用于资源受限的计算环境中,例如电子标签RFID.随着物联网的快速发展,物联网终端传感器部件广泛部署,对轻量级密码体制的需求也越来越大.由于轻量级分组密码具有较低的实现成本和较低的能耗,在物联网终端、卫星通信网络中大量部署轻量级密码算法可以带来显著的社会经济效益.
分组密码的典型结构包括Feistel结构和SPN结构等.这两种结构已经得到广泛深入的研究[2,3].切片(bit-slice)整体上属于SPN结构,最早由Eli Biham于1997年提出[4],是一种构建轻量级分组密码的重要技术之一.当前Present[5]、SERPENT[6]、Rectangle[7]、Keccak[8]等密码均采用了这一技术来设计算法.
安全是密码算法得以应用的前提.近年来,分组密码的安全性评估已取得长足的进步.特别是,基于混合整数线性规划(MILP)方法[9-11]的提出,使得分组密码算法安全分析朝着自动化、精细化、标准化、可证明方向发展.
本文主要描述了一种轻量级的分组密码算法FBC.该算法主要基于Feistel结构设计,并以Feistelbased Block Cipher的首字母命名.FBC算法主要包括FBC128-128,FBC128-256和FBC256-256三个版本,分别支持128和256两种比特长度的明文分组以及128和256两种比特长度的密钥.在整体结构上,FBC算法采用4路两重Feistel结构设计.在保持结构简洁的同时我们通过增加两个异或操作的微小代价较大提高FBC算法整体结构的扩散特性.非线性函数F采用切片技术.其中,S盒基于NFSR构造,其各项密码学性质达到最优,同时硬件实现代价达到最小,为最轻的S盒之一;线性变换L仅由循环移位和异或构成,具有较好的密码学特性的同时兼顾好的软硬件实现效能.在安全性方面,我们基于混合整数线性规划(MILP)寻找最少活跃S盒个数的方法对其进行差分、线性、不可能差分以及积分等方法的分析.实验结果表明,FBC可以抵抗上述各种攻击方法的攻击.FBC算法不仅具有结构简洁,轻量化,安全性高等特性,还具有灵活高效的软硬件实现方式,可以满足不同平台的应用需求.
本文余下章节安排如下:第2节详细描述了FBC算法规范流程;第3节给出了FBC算法设计准则;第4节给出了FBC算法部件的安全属性,并在第5节给出了算法的整体安全评估结果;最后在第6节对算法的软硬件实现性能作了简单评估.
2 算法规范
本节详细描述了轻量级分组密码FBC的算法流程,包括密钥扩展算法、加密过程和解密过程.其不同版本以格式FBC n-m统一进行命名,其中n为明文分组比特长度,m为主密钥比特长度.
2.1 算法参数
FBC不同版本的状态均由4个w比特的字组成,其中字长w与明文分组长度n的关系满足w=n/4.设r为迭代轮数.FBC算法主要参数见表1.

表1 FBC主要参数Table 1 Main parameters of FBC
2.2 符号
本文主要使用下面的一些符号:
P: n比特明文
C: n比特密文
ki: 第i个子密钥,i=0,1,···,2r+1
ai,bi,ci,di: 第i轮迭代的状态字,每个字的长度为w比特,i=0,1,···,r+1
u,v: 长度为w比特的字
ui,vi: 字u和v的第i个长度为w/4比特的子块,i=1,2,3,4
ui[j],vi[j]: 子块ui和vi的第j比特,j=0,1,2,···,w/4-1
1: 长度为w比特的全1子块
和运算符:
⊕:面向比特的异或运算
&:面向比特的与运算
‖:字符串连接符
2.3 算法描述
2.3.1 算法结构
FBC算法基于4路两重Feistel结构设计,非线性函数F采用切片技术构造,算法主体结构如图1.
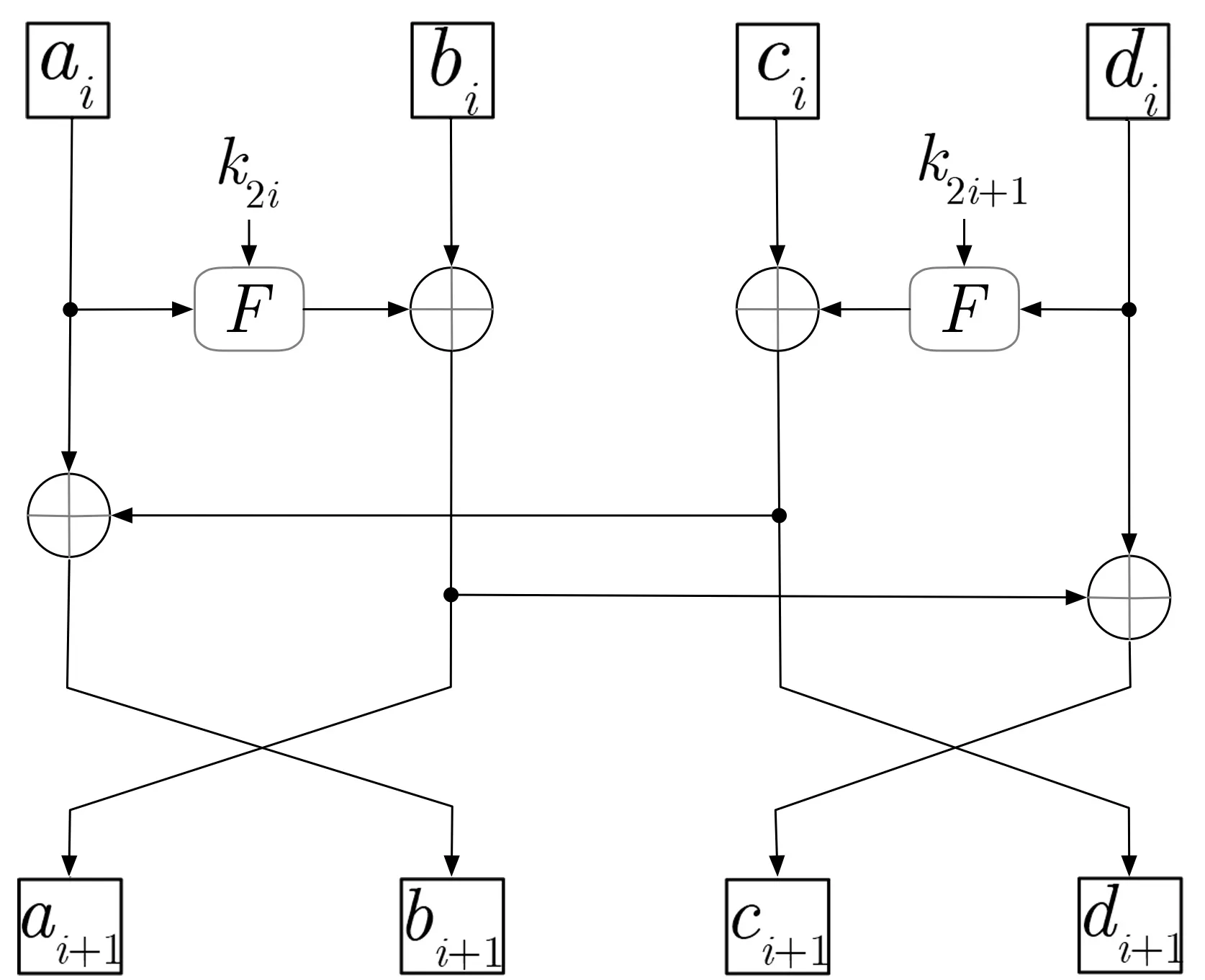
图1 FBC算法结构图Figure 1 Structure of FBC
2.3.2 非线性函数F
非线性函数F的输入包含2个w比特的字x和y,输出一个w比特的字z,记z=F(x,y).具体运算过程如下.
(1)子密钥加:u=x⊕y.
(2)列变换:将u二进制表示分解成4个等宽的字符串,每个字符串包含w/4个比特,即u=u1‖u2‖u3‖u4,令:
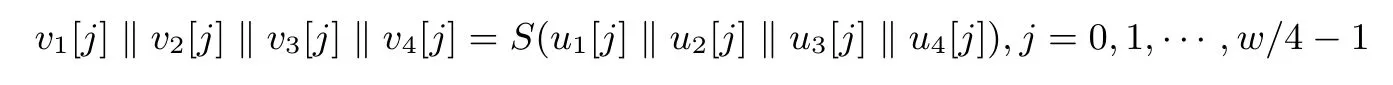
这里S为4进4出的S盒变换,见表2.记v=v1‖v2‖v3‖v4.
(3)行变换L:
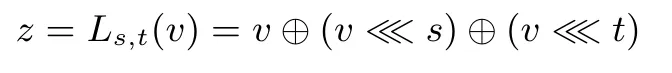
在行变换Ls,t(v)中参数s,t取值与w有关,见表3.

表2 S盒真值表Table 2 Truth table of S-box

表3 L线性变换中循环参数s,t取值Table 3 Value of s,t in linear transformation
2.3.3 密钥扩展算法Expand Key
针对FBC128-128和FBC256-256,将m比特主密钥k分成4个w比特的字k0,k1,k2,k3,即k=k0‖k1‖k2‖k3.对i=0,1,···,2r-5,计算
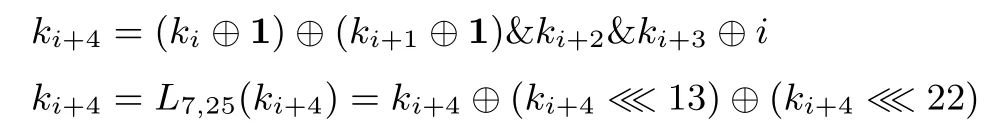
针对FBC128-256,将256比特主密钥k分成8个32比特的字k0,k1,k2,···,k7,即k=k0‖k1‖···‖k3.对i=0,1,···,2r-9,计算
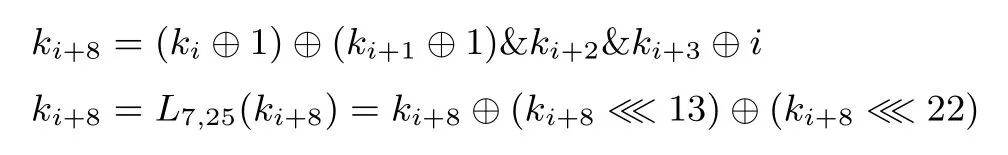
2.3.4 加密过程
(1)首先根据2.3.3节密钥扩展算法将主密钥k扩展成子密钥序列ki,i=0,1,···,2r-1;
(2)将输入明文块P分成4个长度为w比特的子块,即P=a0‖b0‖c0‖d0.重复执行下列操作r-1次(Round Func):
(a)ai+1=F(ai,k2i)⊕bi
(b)ci+1=ai+1⊕di
(c)di+1=F(di,k2i+1)⊕ci
(d)bi+1=di+1⊕ai
(3)然后执行下列操作1次(FinalRoundFunc)(不交换顺序):
(a)br+1=F(ar,k2r-2)⊕br
(b)dr+1=br+1⊕dr
(c)cr+1=F(dr,k2r-1)⊕cr
(d)ar+1=cr+1⊕ar
(4)最后输出密文块C=ar+1‖br+1‖cr+1‖dr+1.
2.3.5 解密过程
(1)首先根据第2.3.3节密钥扩展算法将主密钥k扩展成子密钥序列ki,i=0,1,···,2r-1;
(2)将输入密文块C分成4个长度为w比特的子块,即C=a0‖b0‖c0‖d0.首先执行下列操作1次:
(a)a1=a0⊕c0
(b)b1=F(a1,k2r-2)⊕b0
(c)d1=b0⊕d0
(d)c1=F(d1,k2r-1)⊕c0
(3)然后对i=1,2,···,r,重复执行下列操作r-1次:
(a)ai+1=bi⊕di
(b)bi+1=F(ai+1,k2(r-i)-2)⊕ai
(c)di+1=ai⊕ci
(d)ci+1=F(di+1,k2(r-i)-1)⊕di
(4)最后输出明文块P=ar+1‖br+1‖cr+1‖dr+1.
3 设计准则
本节给出了设计FBC算法时的一些参考准则,包括整体设计准则和部件设计准则两大类.
3.1 整体设计准则
FBC算法整体上遵循简单、简洁、轻量、高效、安全等准则设计.其主要体现于:
·简单:FBC算法基础运算部件简单,仅仅由通用部件异或、循环移位、逻辑与和S盒等构造.整个加解密过程和密钥扩展过程均简单明了.
·简洁:FBC算法结构简洁,整体采用4路两重Feistel结构设计,F函数基于切片技术构造,整个算法没有任何冗余操作.
·轻量:FBC算法部件采用轻量化设计,其中S盒基于NFSR构造,硬件实现仅需5个非门、4个或门和4个与门.线性变换L每个输出比特仅需2个或门.密钥扩展同样采用轻量化设计,每轮子密钥比特硬件实现仅需2个非门,4个异或门和2个与门.
·高效:FBC算法具有多种高效的软硬件实现方法.在软件实现方面,可以采用4进w出或者8进w出表实现,亦可采用无查表快速逻辑实现方法进行实现;在硬件实现方面,局部可以基于NFSR对S盒和密钥扩展高效实现,整体既可以同时实现左右两路Feistel结构也可以只实现一侧Feistel结构.
·安全:FBC算法整体采用4路两重Feistel结构,F函数采用切片技术构造,局部属于SPN结构,其中S盒选择的是密码学性质最优的S盒,置换P选择差分/线性分支数为4的线性变换L,在结构上没有弱点.只要迭代足够的轮数,整个算法就具有较高的安全性.
3.2 部件设计准则
3.2.1 S盒
S盒在设计时主要遵循了如下准则:
·4进4出的置换
·具有最优的差分均匀度和非线性度
·至少有一个分量布尔函数代数次数为3
·没有不动点
·轻量化
·具有高效的软件实现
·在上述条件下硬件实现代价最低
根据上述准则,我们选择基于4级NFSR来构造最优的4进4出S盒.其中NFSR反馈函数f选择如下:
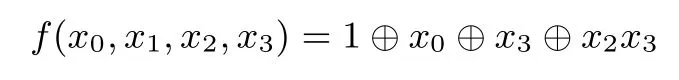
设由f定义的NFSR生成的序列的前8项为x0x1x2x3x4x5x6x7.令x=x0x1x2x3和y=x4x5x6x7.则NFSR诱导出到上的一个置换S:y=S(x).
3.2.2 线性变换L
线性变换L在设计时主要遵循了如下准则:
·w进w出的线性置换
·差分分支数和线性分支数不低于4
·具有最高的周期
·具有最少个数的不动点
·具有最优的全扩散特性
·简单,便于软硬件实现
·轻量化
根据上述准则,我们选择如下仅由异或和循环移位两种运算构成的线性变换:
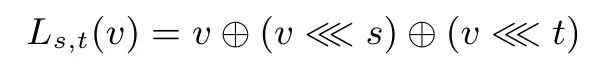
其中参数s,t取值与w有关,见表3.
3.2.3 密钥扩展
密钥扩展在设计时主要遵循了如下准则:
·非线性置换
·简单
·轻量化
·高效软硬件实现
·能抵抗滑动攻击
根据上述准则,我们采用类似切片技术设计了密钥扩展,在纵向列变换上采用M序列构造方法,在横向行变换上面采用线性变换L,在满足轻量化需求下达到快速混淆和扩散的目的.
4 部件分析
4.1 S盒
定义1 (代数次数)设正整数n.一个n×n的S盒是到上的一个映射:s=(f1,f2,···,fn),这里fi(1≤i≤n)均是n元布尔函数.S盒s的代数次数为其分量函数的线性组合的最低代数次数,即:
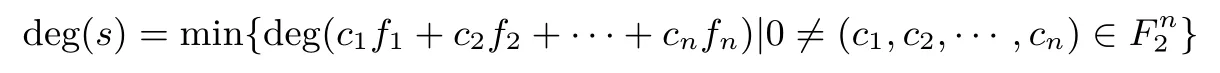
定义2 (非线性度)对于一个n×n的S盒y=s(x),定义S盒s的非线性度为
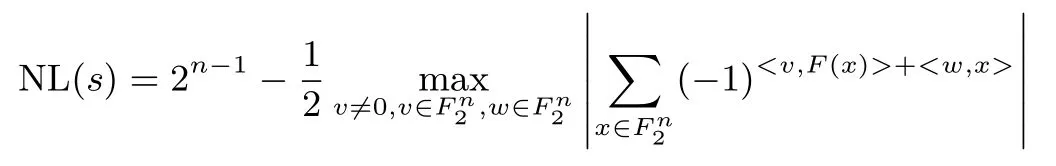
其中<,>表示内积运算.
定义3 (差分均匀度)对于一个n×n的S盒y=s(x),定义
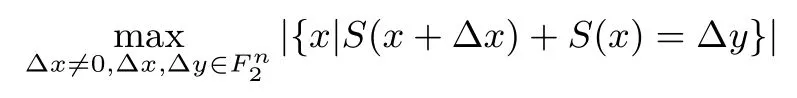
为该S盒s的差分均匀度.
定义4 (图代数免疫度)对于一个n×n的S盒y=s(x),定义
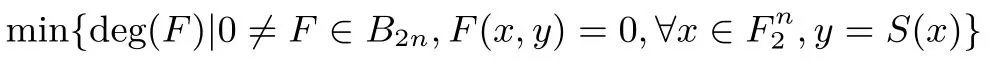
为该S盒s的图代数免疫度.
定义5 (不动点)对于一个n×n的S盒y=s(x),称满足s(x)=x的解为S盒的不动点.
对于FBC算法选择的4进4出的S盒的密码性质见表4,其差分均匀性、非线性度、图代数免疫度都达到了最优,没有不动点.

表4 S盒密码学指标Table 4 Cryptographic properties of S-box
4.2 线性变换L
定义6 (线性变换)有限域Fq上的一个变换L被称之为是Fq上的n维线性变换,是指其对任意X,Y∈,c∈Fq,均满足
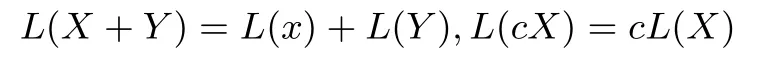
定义7 (差分分支数)对一个线性变换L:→,Y=L(X),可以用矩阵的形式表示,即存在Fq上的一个n×n的矩阵M,使得对任意X,有Y=L(X)=M X.线性变换L的差分分支数定义为
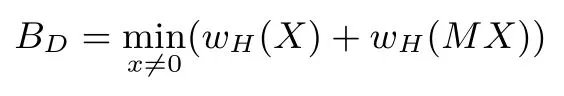
其中wH(X)是X的汉明重量,也就是非零分量的个数.
由定义可知,一个线性变换L的差分分支数总是小于等于n+1.
定义8 (线性分支数)对线性变换有Y=L(X)=M X,其线性分支数定义为
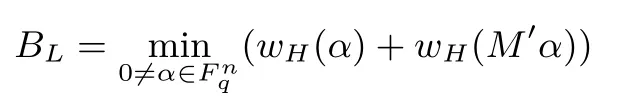
这里M′表示矩阵M的转置.
定义9 (周期)对任意给定的非零变换P和正整数i,定义
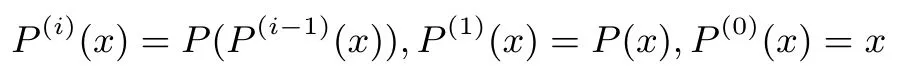
称使得对所有x均有P(i)(x)=x成立的最小正整数i为变换P的周期.
对于FBC算法族选择的线性变换Ls,t,其密码性质如下:

表5 线性变换Ls,t的密码学指标Table 5 Cr yp togr ap hic p rop er ties of Ls,t
5 安全性评估
5.1 差分分析
差分分析是最初由Biham E和Shamir A于1991年针对DES算法提出的一种密码分析方法[12].该方法几乎适用于所有的分组密码体制,是对分组密码算法威胁最大的分析方法之一[13-15].对于采用S盒作为核心部件的分组密码算法,评估单条差分传播路径最大概率上界的最有效方法就是估算差分传播路径中活动S盒的个数.2011年Mouha N等人[9]利用混合整数线性规划MILP给出差分分析和线性分析中活动S盒个数下界的评估方法.他们首先将差分分析和线性分析中活动S盒传播规律用线性不等式刻画,目标函数为最小的活动S盒个数,然后利用求解MILP问题的软件进行求解,如Cplex、Gurobi等.该方法得到的下界精度较高,许多时候达到最优值,因此被广泛用来作为评估分组密码抵抗差分分析和线性分析能力的参考指标.
对FBC算法,我们采用MILP方法搜索了差分分析中活动S盒的最少个数.由于采用原始方法利用线性不等式直接刻画S盒s和线性变换L以及异或⊕等运算涉及的变元个数和不等式个数均较多,运行Gurobi等软件时能够求解的轮数太少,时间太长,效率太低.故我们采用一种简化的办法来求解活动S盒的个数.该方法可以求解FBC算法全轮迭代过程中活动S盒的个数,具体刻画过程见附录A.需要说明的是,该方法得到的下界并不一定是真实差分分析中的活动S盒个数的精确下界,有时甚至相差很大.因此其结果仅仅作为一种参考.
作为结果,对FBC128-128、FBC256-256达到安全界的迭代轮数为32和64,而实际算法迭代轮数为48和80,我们认为它们完全可以抵抗差分密码分析;对FBC128-256,迭代64轮时活动S盒个数为128,刚好达到安全界.如果考虑到分组密码剥离轮技术的应用,通过该方法估算的活动S盒个数会低于64.正如上面所说,一方面我们的MILP方法估算活动S盒个数结果很粗糙,虽然它是一个下界,但是离精确的下界可能相差很大,另外一个方面,在实际差分密码分析中,真实差分路径的概率往往比确切活动S盒个数估算的界往往小非常多,因此我们依然相信FBC128-256对于差分分析来说是安全的.
5.2 线性分析
线性分析最初由Matsui M于1993年针对DES算法提出的一种密码分析方法[16].与差分分析相似,该方法同样适用于所有的分组密码体制,是对分组密码算法威胁最大的分析方法之一[17-19].对于采用S盒作为核心部件的分组密码算法,评估单条线性迹(即线性掩码传播路径)的最大偏差概率的上界的最有效的方法就是估算线性迹中活动S盒的个数.类似于差分分析,我们同样采用简化的MILP方法对其线性迹中活动S盒的传播规律作了刻画,其可以求解FBC全轮迭代过程中活动S盒的个数,具体刻画过程见附录B.
作为结果,对FBC128-128、FBC256-256达到安全界的迭代轮数为32和64,而实际算法迭代轮数为48和80,我们认为它们完全可以抵抗线性密码分析;对FBC128-256,迭代64轮时活动S盒个数为128,刚好达到安全界.同样的道理,我们相信FBC128-256对于线性分析来说也是安全的.
5.3 不可能差分分析
不可能差分是差分分析的一种变体[20-22],也是一种常见的密码分析方法.对于不可能差分分析,我们同样利用MILP方法来搜索FBC最长轮数的不可能差分模式,具体的转化MILP不等式方法与差分分析类似,不再赘述.我们在具体分析中构建了三种MILP模型,在有限的计算资源下,可得到FBC128-128和FBC128-256的7轮不可能差分和FBC256-256的13轮不可能差分.下面给出三种模型的构造方法,由已知的不可能差分分析结果来看,几乎所有的不可能差分路径的输入和输出差分模式分别只有一个活跃S盒,因此,三种模型中,选定输入输出差分时,应满足该输入(输出)只能使单个S盒活跃.
·M1:变量基于比特,将第一轮的输入差分和最后一轮的输出差分信息(α,β)添加到搜索i(i从第一轮开始遍历)轮差分路径的模型中,去掉目标函数,判断该模型有无解即可.若i轮模型无解,说明存在i轮的不可能差分路径(α,β),继续搜索i+1轮;若i+1轮有解,不再遍历i+1轮之后的模型,此时不可能差分路径(α,β)轮数最长为i.遍历输入输出差分(α,β),重复上面过程,则可得到最大轮数的不可能差分和对应的差分选取模式.
·M2:用到Sasaki和Todo提出的方法[23],同M1类似,不同在于对S盒的刻画.这里对于S盒来说,任意的非0输入差分经过S盒都可以得到任意的非0输出差分,因此S盒的刻画只需要两个不等式,而且遍历差分模式时,只需要对活跃S盒的位置进行遍历,S盒的输入输出任意取值即可.搜索过程与M1相同.
·M3:将S盒作为变量,则只需刻画轮函数的线性层即可,相对于上述两种模型,变量减少大概4倍.遍历输入输出差分模式时,遍历活跃S盒的位置即可,搜索过程同上.
上述三种方法各有优劣.M1遍历所有的输入输出差分,即使规定活跃S盒个数为1,要搜索的模型个数也是远远大于其他两种,因此搜索时间最长;当轮数较大时,M3能快速给出模型是否有解,效率上M3>M2>M1;但由于M1遍历所有输入输出差分,M2取定S盒的某个输入输出,M3只是遍历S盒位置,因此在轮数大小上M1>M2>M3.
在FBC128实验中,对于M1和M2,由于计算能力有限,第八轮就已经不能计算出结果,第七轮无解;M3虽然可判断的轮数大,但是M3在第七轮之后的所有轮数都有解.三个模型给出的结论一样,目前只能搜索到7轮不可能差分.

表6 FBC算法不可能差分分析结果Table 6 Impossible differential analysis of FBC
5.4 积分分析
积分分析可以看出是一种代数攻击,其主要寻求关于若干输入明文比特的零和区分器.可分性(division property)是目前分析对称密码算法积分性质最有力的工具[24,25],其同样可以借助MILP的方法方便快速地搜索算法的积分区分器.借助可分性可以搜索得到FBC128-128和FBC128-256算法的7轮积分区分器,受限于计算能力,目前还无法断定FBC128-128和FBC128-256是否存在8轮积分区分器.FBC256-256可以搜索得到10轮积分区分器,但是目前同样无法断FBC256-256是否存在11轮积分区分器.
5.5 零相关分析
零相关分析是线性分析的一种变体[26],也是一种常见的分组密码分析方法.类似于不可能差分分析,我们利用MILP方法搜索FBC算法族零相关的最长轮数.构造模型的方法同不可能差分分析的M3,区别在于对轮函数线性层描述与差分分析的相反,但实验结果同不可能差分结果一样,对于FBC128-128和FBC128-256的零相关分析,目前能找到的最大轮数为7.对于FBC256-256的零相关分析,目前能找到的最大轮数为13.
6 软硬件性能评估
6.1 软件性能评估
FBC算法具有灵活高效的多种软件实现方式,包括快速无查表实现、4进w出查表实现、8进w出查表实现,在内存允许的条件下,甚至可以做成16进w出的查大表实现.其中查表实现方法类似于AES算法的查表实现,只是对FBC而言,需要细心调整明密文和密钥比特的位置.下面我们详细给出了快速无查表实现方法,具体过程如下:

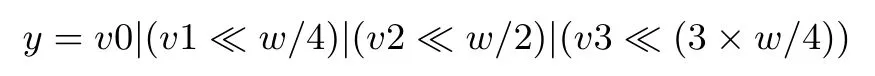
注:这里bitmask_const为比特掩码常量,其为宽度为w/4的全1字符串.
从上述快速实现方式中,可以看出,函数F可以通过7个异或,7个逻辑与运算,6个非运算(与全1常量异或运算可以看成是非运算),6个移位运算,3个或运算共29个基础运算就可以实现.
因此FBC算法的一轮迭代只需要29+4=33个基础运算便可以实现.整个加密过程和解密过程只需要33r个基础运算就可以完成.
6.1.1 软件测试结果
在64位Windows以及32位ARM环境下,对FBC算法的加解密速率进行了测试,测试环境见表7,结果取105次CBC模式运算测试结果的平均值为加/解密速率,如表8所示.

表7 FBC算法软件测试环境Table 7 Software test environment of FBC
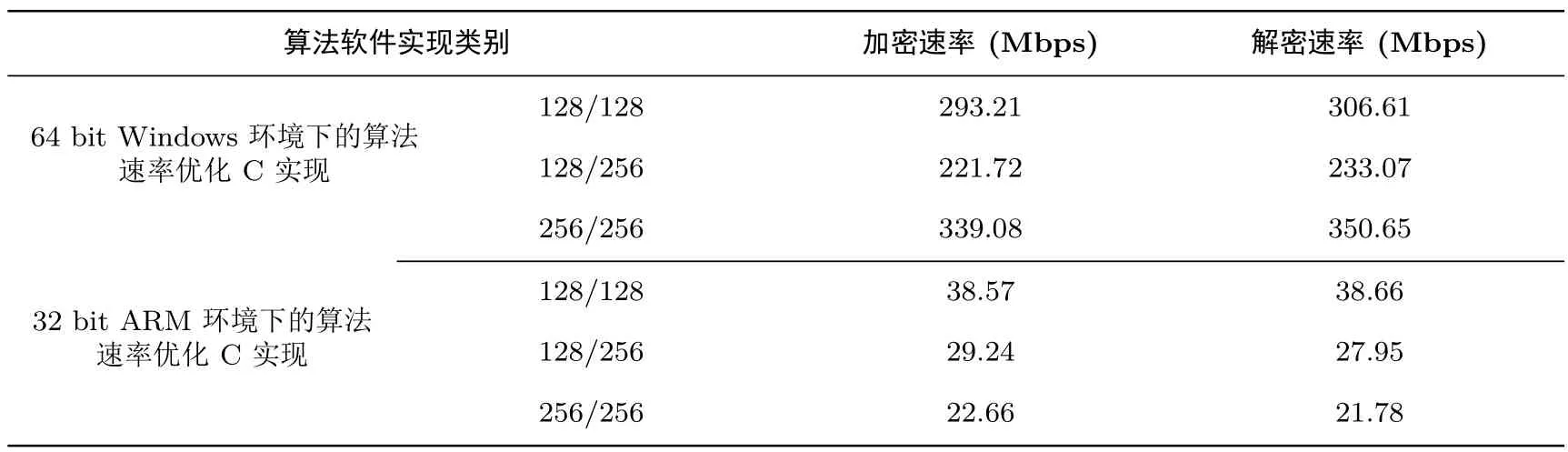
表8 FBC算法软件测试结果Table 8 Software implementation rate of FBC
6.2 硬件性能评估
6.2.1 硬件实现概述
FBC算法所有版本均可以轻量化实现.正如3.2.1节所示,S盒可以采用NFSR方式实现,此时需要4个与门,4个异或门,5个非门.而对于线性变换L,每比特需要2个异或门.因此实现函数F,需要w个与门,3w个异或门和5w/4个非门.
对于FBC算法的轮函数可以采用多种方式实现.一种是同时实现4路两重Feistel结构,此时需要2w个与门,10w个异或门和5w/2个非门.另外一种是只实现2路Feistel结构,另外2路采用重复调用即可.此时需要w个与门,5w个异或门和5w/4个非门就可以了.当然在Feistel结构内部,我们还可以更小宽度来实现轮函数,此时需要的硬件门数更少.
从上面的讨论可知,FBC算法的硬件实现代价非常低.
6.2.2 Verilog仿真实现测试结果
对FBC算法进行了Verilog硬件仿真实现测试,测试环境为基于Xilinx公司的ISE Design Suite 14.7软件工具和Xilinx virtex 5 FPGA芯片.结果如表9所示.
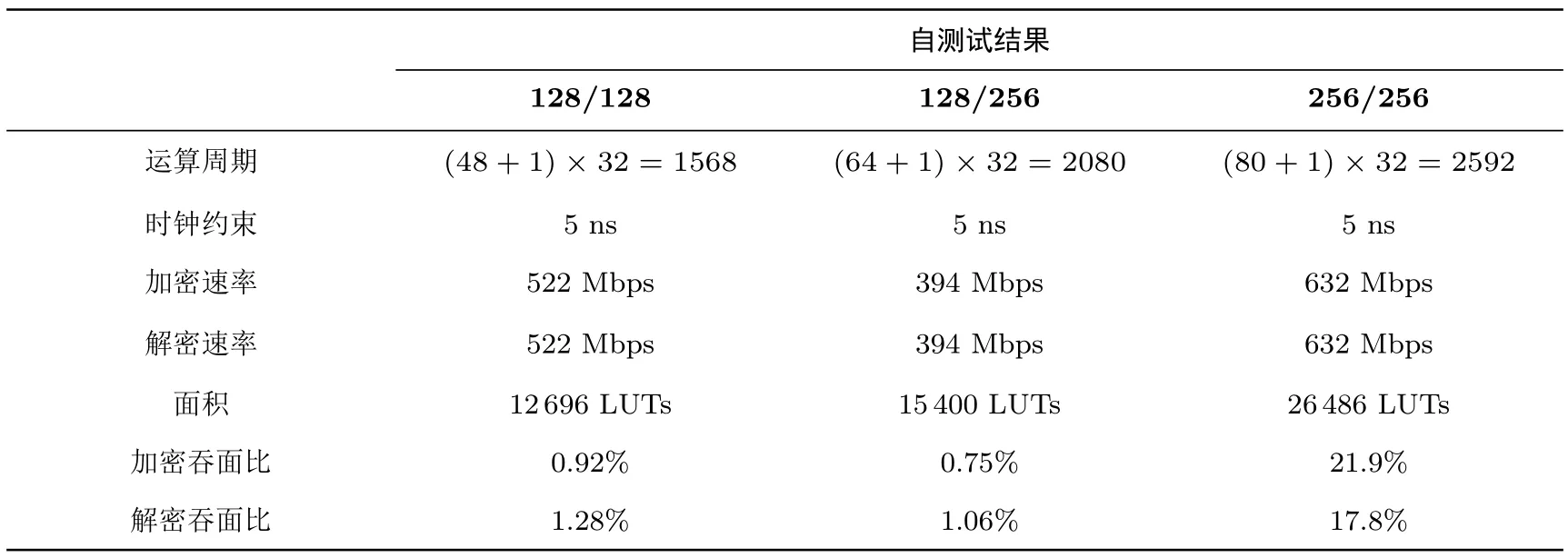
表9 FBC算法Verilog硬件仿真测试Table 9 Verilog hardware simulation test of FBC
致谢
本文作者衷心地感谢武汉大学唐明教授团队对FBC算法的硬件评估进行了Verilog仿真实现,并给出了相应结果.
附录A差分分析活动S盒个数不等式刻画求解
下面以FBC128-128为例介绍MILP具体分析过程.
设F函数的输入记作(x,k),这里k表示相应的轮密钥.设x=(x0,x1,···,x31)∈{0,1}32,将其写成如下形式:

注意到线性变换L(x)=x⊕(x⋘3)⊕(x⋘10),x的每一列经过L变换后仍然在同一列中.引入二元变量组(a0,a1,···,a7),分别对应x的每一列,即每个S盒,ai刻画第i列的活动S盒,即当该列为零时,即对应的S盒输入没有差分,ai取值为0;否则取值为1.接下来我们对轮函数用线性不等式刻画,将最少活动S盒个数作为目标函数并构造相应的MILP问题,最后用Gurobi求解目标值.
(1)对函数F的差分模式的不等式刻画
设(a0,a1,···,a7)表示F函数的输入差分模式,(b0,b1,···,b7)表示F函数的输出差分模式.为了刻画L(x)=x⊕(x⋘3)⊕(x⋘10)变换的输入输出差分模式,我们穷尽L变换的所有输入,最后我们发现输入输出差分重量之和为4的只有下列8种.

而其余情况其重量或者为零或者大于等于6.于是我们用线性不等式刻画如下:

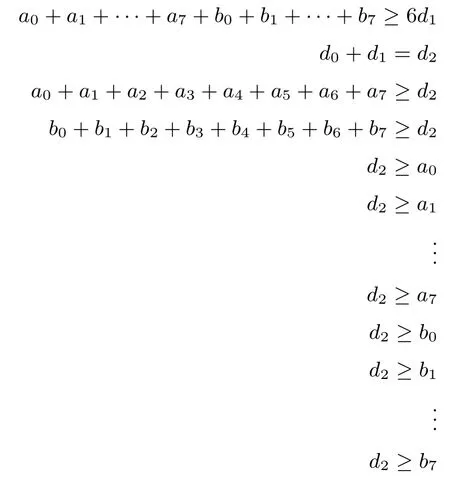
这里d0,d1和d2为引入的辅助变量,这三组变量的取值均为{0,1}.
(2)对轮函数的差分模式的不等式刻画
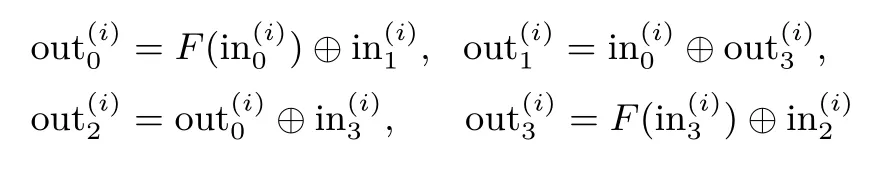
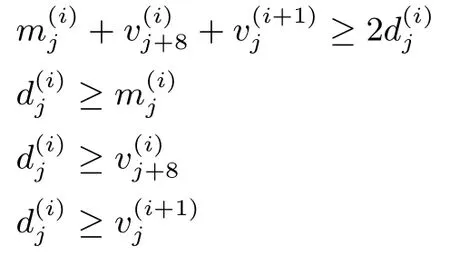
同理需要对
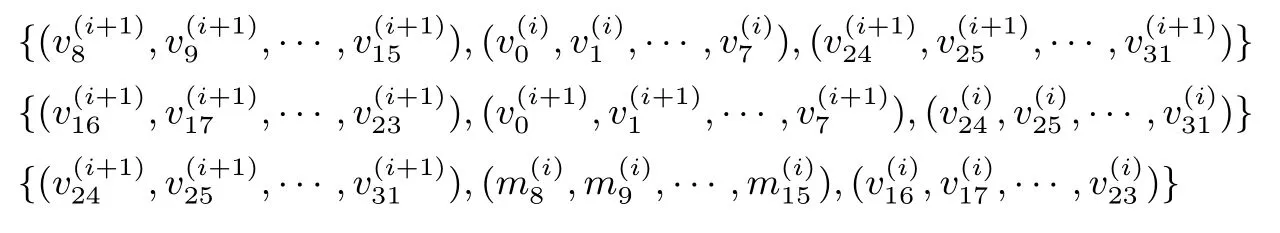
做相应的不等式刻画.
(3)限制条件刻画
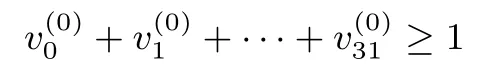
该不等式表示输入差分不为零.
其次,所有变量取值范围均为{0,1}.
(4)目标函数刻画

这里n表示轮数.
我们利用Gurobi运行该MILP问题,当轮数为32时,活动S盒的个数为64;当轮数为64时,活动S盒的个数为128.
附录B线性分析活动S盒个数不等式刻画求解
下面以FBC128-128为例给出了其MILP分析过程.
设x=(x0,x1,···,x31)∈{0,1}32表示F函数的输入,引入二元变量组(a0,a1,···,x7),分别对应x的每一列,即每个S盒.ai画第i列的活动S盒,即当该列为零时,即对应S盒的输入线性掩码为0,ai取值为0;否则取值为1.然后我们对轮函数用线性不等式刻画,将最少活动S盒个数作为目标函数并构造相应的MILP问题,最后用Gurobi求解目标值.
(1)对F函数的线性掩码模式的不等式刻画
设(a0,a1,···,x7)表示F函数的输入线性掩码模式,(b0,b1,···,b7)表示F函数的输出线性掩码模式.根据线性掩码与差分的对偶性,此时我们穷尽线性变换LT(x)=x⊕(x⋘3)⊕(x⋘10)(该线性变换为L(x)的转置)的所有输入,最后我们发现输入输出线性掩码重量为4的只有下列8种可能.

而其余情况其重量或者为零或者大于等于6.我们用线性不等式刻画如下:
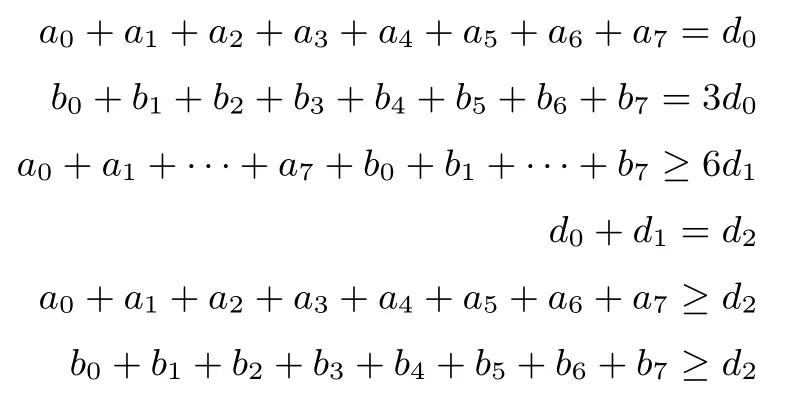
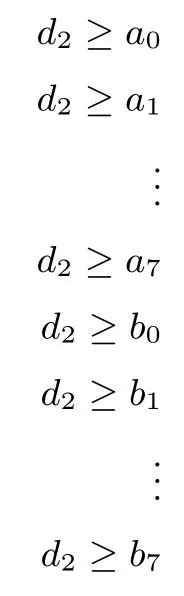
这里d0,d1和d2为引入的辅助变量,这三组变量的取值均为{0,1}.
(2)对轮函数的线性掩码模式的不等式刻画

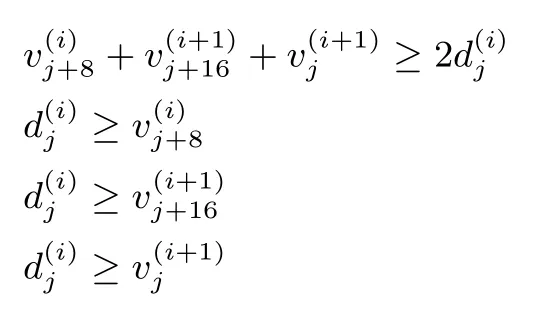
同理需要对
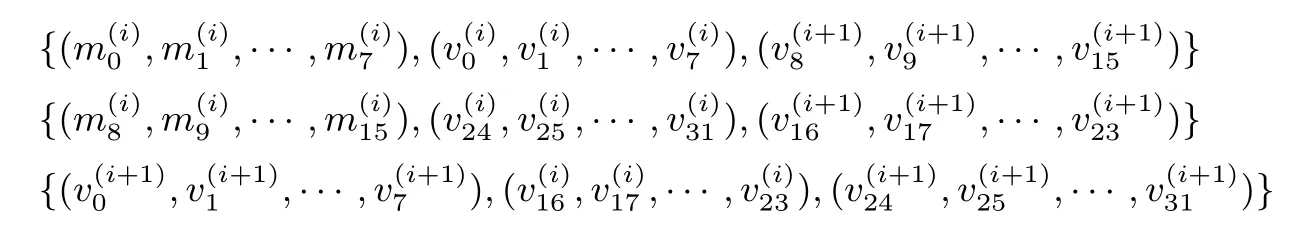
做相应的不等式刻画.
(3)限制条件刻画
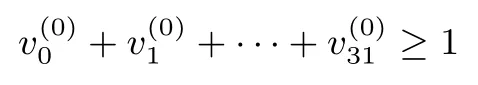
该不等式表示输入线性掩码不为零.
其次,所有变量取值范围均为{0,1}.
(4)目标函数刻画
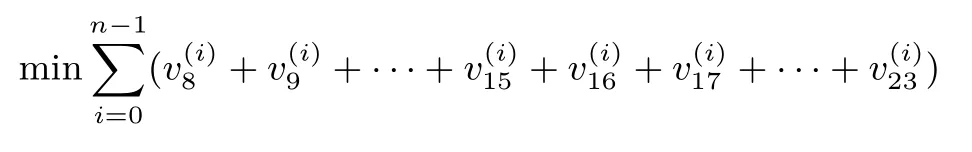
这里n表示轮数.
事实上,线性掩码模式的不等式刻画与差分模式的不等式刻画完全等价,我们利用Gurobi运行该MILP问题,当轮数为32时,活动S盒的个数为64;当轮数为64时,活动S盒的个数为128.

