双向蝴蝶形钢板墙抗震性能有限元研究

丁志昌， 李启才， 薛志杰， 黄 燊

（苏州科技大学 土木工程学院，江苏 苏州215011）

20 世纪以来，钢板剪力墙因其优异的抗震性能逐渐研究热点，并广泛应用在中高层钢结构中[1]。 带加劲的钢板剪力墙以及厚钢板具有水平刚度大、承载力高、耗能性能等优点，因此日本在实际工程中多采用此类钢板。而随着薄钢板理论逐渐完善，尤其是薄板屈曲后性能的发展，北美倾向于使用薄钢板。然而在实际应用中， 由于拉力带的作用使得周边框架受到附加的斜拉力而提前破坏， 因此该结构对柱刚度有阈值要求[2]。Hitaka 等[3]提出了带缝钢板剪力墙的概念，改变其受力性能，变形以柱状部的弯曲变形为主，削弱了拉力带的作用，并给出了相应的弹性抗侧刚度和承载力的理论计算公式。 近年来，国内外学者通过大量的开缝钢板墙试验及模拟究取得了一定成果：开缝钢板剪力墙延性和耗能优异，且可以通过调整其几何参数满足不同的承载力和刚度要求，但是同时，也存在部分试件竖缝杆过早面外失稳、局部应力集中严重而导致钢板撕裂等问题[4-7]。 基于上述问题，Ma[8]于2010 年提出了蝴蝶形钢板墙的概念，用蝴蝶形耗能段取代柱状耗能段，以期更多的截面边缘屈服而提高材料利用率，此外，还给出了蝴蝶板的弹性抗侧刚度和承载力公式。

课题组基于前人的研究成果提出了一种新型开孔形式的钢板剪力墙，双向蝴蝶形钢板剪力墙（Doubledirectional Butterfly-shape Steel Plate Wall，DBSPW），并进行了试验研究，在此基础上采用数值模拟进行参数分析，在验证有限元软件的可靠性之后，建立HN（Horizontal number）、HS（Horizontal size）、VN（Vertical number）和 VS（Vertical size）四个系列分别研究横向蝴蝶杆行数、尺寸以及竖向蝴蝶板数量、尺寸对其承载力，耗能，延性和刚度退化等整体性能的影响。

1 钢板模型与参数

1.1 双向蝴蝶形钢板剪力墙

图1 钢板构造与几何参数

双向蝴蝶形钢板剪力墙的构造见图1， 钢板可以看成由槽钢约束的竖向蝴蝶板和横向蝴蝶杆两部分组成。 该新型开孔钢板的设计目标是在加载过程中槽钢约束的竖向蝴蝶板承担主要水平力， 横向蝴蝶杆通过变形协调产生塑性变形在加载中前期以耗散大部分的能量输入而在加载后期与竖向蝴蝶板协同耗能，且可以通过调整两者数量以及尺寸实现结构性能可调。 槽钢作为面外约束可以限制钢板的整体变形，进而防止钢板因面外变形过早丧失承载力，同时也加强横向蝴蝶杆的端部条件，确保其发生面内的弯剪变形。 课题组针对新型双向蝴蝶形钢板剪力墙进行了4 块足尺试件的水平低周反复荷载试验，试验结果表明该新型钢板有较大的初始刚度和承载力，整体面外变形小，滞回饱满，实现了设计目标。

1.2 有限元模型的建立

本文采用Abaqus/standard 对双向蝴蝶形钢板剪力墙进行数值模拟，基于课题组进行的足尺试验中的一个试件实测数据验证软件模拟的可靠性，该试件记为Base 试件，其有限元模型见图2。 模型由框架梁、框架柱、钢板和槽钢组成，其中框架梁和柱采用梁单元，截面形式为H 型钢，尺寸与试验铰接框架一致，柱为H250×250 ×12×16，梁为 H350×220×12×16；内填钢板和槽钢采用 Abaqus 中 8 节点缩减积分的 Solid185 实体单元，几何尺寸参照试验实际尺寸，详见表1 中Base 试件。

梁柱连接采用有限元软件自带的加入单元模拟试验框架的铰接节点， 采用Tie 约束简化处理内填板与铰接框架之间的连接以及钢板与槽钢之间的螺栓连接。 此外钢板和槽钢之间采用面面接触模拟接触面之间的相互作用。 约束钢板底部所有自由度以模拟试验中的底部固接，柱下端放松URZ（框架平面内的弯曲转动）模拟铰接，为了防止框架面外失稳以及发生扭转，约束梁柱平面外的UZ（框架平面外的位移）和URY（梁柱绕轴线方向的转动），试验中通过与上梁固定的加载梁施加荷载，为了模拟这种均匀加载方式，耦合框架梁上翼缘表面所有节点的UX 自由度。

模型中钢板和槽钢材性采用线性随动强化模型，弹性模拟E及屈服强度和极限强度均按材性试验输入，强化阶段钢材的切线模型为0.04E，泊松比为ν=0.3；梁和柱材性只设置弹性模量E，同样按材性试验数值输入。数值模拟中需对钢板施加初始缺陷以考虑屈曲对钢板的影响，实际采用一阶模态面外幅值为钢板高度千分之一的方法综合计算。在双向蝴蝶形钢板剪力墙的数值模拟中采用位移控制的往复加载，参考SAC 规范[9]，同试验加载方案一致，考虑到计算所需的硬件和试件成本，每个加载级循环两次。

图2 钢板有限元模型

表1 钢板模型几何参数

1.3 有限元模型的试验验证

图3 有限元和试验滞回对比

为了验证有限元模型的可靠性，图3 给出了试验及有限元在往复荷载作用下的滞回曲线对比。 由图可知，有限元结果虽略大于试验数据，但总体吻合良好，分析认为原因如下：（1）试件在数值模拟中实现的是理想的平面受力体系，铰接钢框架无面外扭转，而在试验中侧向支撑尤其在加载中后期未能有效进行约束，试件有一定面外变形；（2）模拟中采用的钢材为理想的二线性强化本构，未考虑循环损伤，这和实际的钢材在往复荷载下本构有一定差别；（3）试件在制作和安装上均存在少量的误差，尤其是框架的铰接销轴与孔之间的缝隙，需要压实卡死过程。 （4）模拟中为简化竖向蝴蝶板与框架的螺栓连接进行TIE 接触处理，而在试验中发现蝴蝶板有少许拉拔效应，这也降低了试验试件的承载力。 图3 还可以看出试验试件在层间位移角1%左右时承载力出现下降现象，通过对试验过程观察可知由于螺栓并未拧紧，试件发生平面外失稳，但随后受到槽钢约束并没有进一步开展。 图4 给出了试件层间位移角5%时试验和有限元的整体变形图，以及钢板整体变形挤压槽钢产生的局部变形。 有限元数值计算得到滞回曲线虽略大于试验结果，但滞回形状基本一致，且两者整体变形以及局部变形吻合较好发展趋势，因此利用Abaqus 对此类钢板进行参数分析可满足精度要求。

图4 试件变形对比

1.4 参数确定

图1 给出了双向蝴蝶形钢板剪力墙的几何尺寸。 根据文献[8]研究，对于一端固定一端仅滑动的蝴蝶杆，在水平荷载作用下可以调整蝴蝶杆腰部和底部的宽度的比值a/b 来控制截面边缘材料首先进入塑性的位置，避免出现在应力集中、刚度突变等处，同时文中建议将截面首先进入塑性的位置控制在距蝴蝶杆端部四分之一处，由此得到横向蝴蝶杆的a/b 设计为1∶3。 考虑钢板设计目标，本文选取竖向蝴蝶板数量m（蝴蝶杆数目也会发生变化）、横向蝴蝶杆行数n（h 会随着n 的变化发生改变）、横向蝴蝶杆宽厚比α=b/t（保持耗能段高度h 基本不变） 和端部高厚比β=l/t 分为四个系列VN、HN、HS 和HN 以研究不同参数对双向蝴蝶形钢板剪力墙承载力，耗能，延性和刚度退化等整体性能的影响。 见钢板表1 所列。

2 有限元计算分析

2.1 应力云图对比分析

图5 钢板应力云图

图5 给出了各系列试件在层间位移角5%正向加载时的应力云图， 由图5 可知，Base、HN、VN 以及VS系列在最大加载级时横向蝴蝶杆面外变形较小，以面内的弯曲变形为主，端部及竖向蝴蝶板连接处由于刚度突变存在应力集中现象，且试验中发现由于往复折叠疲劳连接处出现钢板撕裂现象，这与该处应力状态相一致。HS 系列以横向蝴蝶杆的宽厚比为参数，HS3、HS2 以及HS1 蝴蝶杆相对Base 试件厚实性逐渐降低，在侧移过程中更易屈曲，因而产生的面外失稳的影响逐渐加大，蝴蝶杆呈现出较大的面外变形。 除上述现象，各试件在加载后期槽钢约束作用降低，对钢板整体变形限制降低，产生局部屈曲，钢板同时挤压槽钢使其产生轻微弯曲。

2.2 滞回曲线

图6 分别给出了Base 试件、HN、HS、VN 以及VS 系列的滞回曲线，考虑到计算成本，模拟中每级荷载循环2 次，共9 级。 由图可知，各系列试件在加载初期（层间位移角0.375%和0.5%）荷载和位移关系表现为线性，均处在弹性工作状态，几乎无耗能耗散。随着加载继续，层间位移角达到0.75%和1%时，各系列试件滞回环开始展开，荷载位移曲线逐渐偏离直线呈现非线性，并且在卸载后残余一定的变形，通过应力云图可知各系列试件横向蝴蝶杆产生弯曲变形，进入塑性产生一定的耗能。 当加载至层间位移角1.5%和2%时，横向蝴蝶杆弯曲变形加大，各试件滞回曲线继续发展，均呈现平行四边形，滞回饱满耗能优异，但各试件残余变形随之加大。 加载后期（层间位移角3%及以后），由于竖向槽钢约束，试件整体面外变形小，横向蝴蝶杆塑性发展充分，残余变形持续增加，各试件滞回饱满，耗能优异。

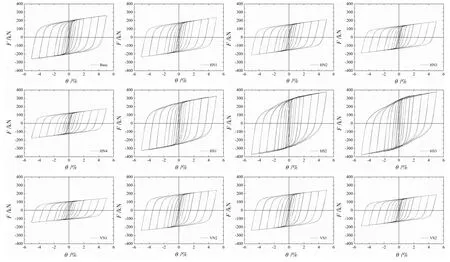
图6 钢板滞回曲线

2.3 骨架曲线

骨架曲线可以直观反映出试件的屈服强度、极限强度、初始刚度以及延性等特性，图7 分别给出了HN、HS、VN 和VS 系列试件的骨架曲线。 由图7 可知， 各试件骨架曲线对称性较好， 在屈服前 （层间侧移角0.75%）近似为一条直线，且具有较高的初始刚度和强度，超过某层间位移角，曲线斜率迅速衰减，但承载力始终缓慢上升，骨架曲线总体上近似呈现出屈服前后的“双直线”特征，表明系列试件均具有较好的延性耗能及抗倒塌性能。

图7 钢板骨架曲线

2.4 耗能能力

试件的耗能能力是评价其抗震性能的一个重要指标，滞回环包围的面积越大，耗散的能量就越多。 本文运用耗能量和无量纲能量耗散系数Ed来描述系列试件的耗能能力， Ed越大， 则反映出试件耗能越充分，耗能能力越好，反之亦然。 能量耗散系数Ed根据图8 进行计算。 图中，SABCD是滞回曲线包络的面积，S△ODF和S△OBC分别为以荷载峰值为顶点的三角形面积；Ed=SABCD/S△ODF+S△OBE。计算各系列试件每个加载级的总耗能量见图9，各加载级能量耗散系数的平均值Ed，见图10。

由图9 可知，各试件总耗能量随层间位移角的增大而提高。 从图10 可知，各试件能量耗散系数呈现几乎一致的变化规律，先迅速增大，然后随加载的继续逐步放缓乃至降低。 原因是横向蝴蝶杆的变形随层间位移角的增加变大，并逐渐进入弹塑性阶段耗能，而到加载中后期蝴蝶杆开始出现面外扭转变形，耗能能力被削弱，故能量耗散系数增长趋势变缓；HS 系列由于蝴蝶杆宽厚比较大，面外扭转现象严重，因此出现能量耗散系数略微降低的现象。

图8 能量耗散系数

图9 试件各加载级总能量

图10 试件的平均能量耗散系数

2.5 刚度退化性能

刚度退化是反映试件损伤累计程度、评定其动力性能的重要因素之一。 本文采用割线刚度Ki来衡量试件的刚度退化情况，其计算公式见式（1）

其中，+P 和-P 各自表示第i 级荷载正向和负向的峰值荷载，+δ 和-δ 则为峰值荷载对应的位移值。 由此计算出的各试件割线刚度Ki见图11；用Ki/K0表示刚度退化系数，作为刚度退化的指标，见图12。

图11 割线刚度Ki

由图中可以看出各系列试件虽然初始刚度存在差异，但其刚度退化系数曲线变化规律一致，随着层间位移角的增大降低，这是因为各试件变形模式类似，加载前期横向蝴蝶杆随着侧移增加进入塑性导致试件刚度迅速退化，加载后期蝴蝶杆塑性变形趋于稳定这是因为在槽钢面外约束下，整个试件进入了平稳的弹塑形强化耗能阶段，此时割线刚度近似等于15%至20%的初始割线刚度，从侧面验证了加载后期竖向蝴蝶板协调耗能的设计理念。

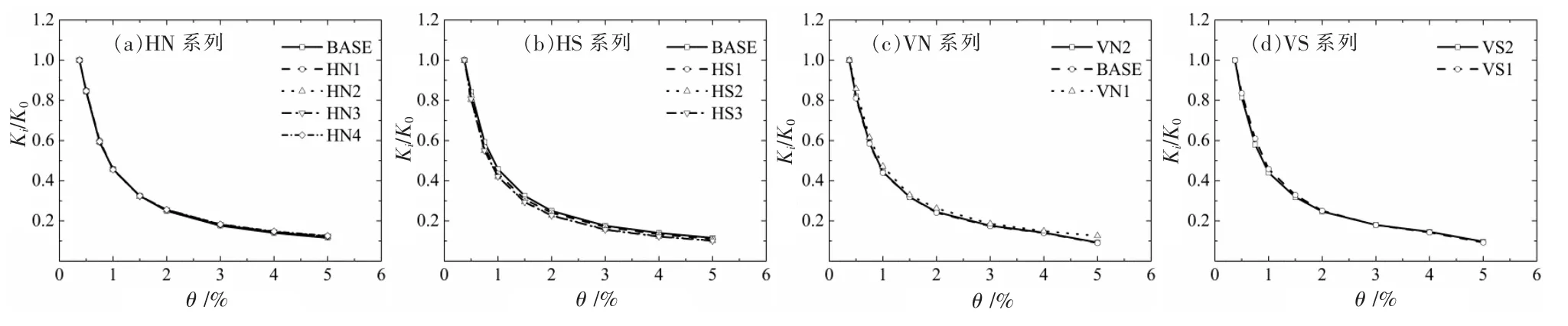
图12 刚度退化系数

3 参数分析

3.1 横向蝴蝶杆行数

横向蝴蝶杆作为主要的耗能段影响钢板整体性能，通过分析Base 和HN 系列试件来考察横向蝴蝶杆数目n 对钢板的影响。 由图6 可知，HN 系列试件滞回曲线饱满，整体呈菱形，且随着横向蝴蝶杆行数n 越大，滞回环越饱满，试件总耗能量越大（由图9 可知）。 根据图7（a）HN 系列试件的骨架曲线可知，由于横向蝴蝶杆数量不同，Base 试件的承载力最高，且随着横向蝴蝶杆行数的减少，试件承载力小幅降低；由图11（a）HN系列试件的割线刚度可知横向蝴蝶杆行数n 对试件初始刚度的影响与其对承载力的影响类似。 综合以上分析，横向蝴蝶杆的数目对双向蝴蝶形钢板墙的承载力和初始刚度影响较小。 由图10（a）HN 系列试件的平均能量耗散系数可知，加载前期横向蝴蝶杆开始进入塑性耗能，因此各试件Ed差异不大，但仍可以看出其随着n 增加而改善；当层间位移角大于2%以后，蝴蝶杆出现面外扭转，各试件耗能能力略微降低，此时能明显发现增加横向蝴蝶杆行数可以提高钢板的耗能能力。

3.2 横向蝴蝶杆比值

根据文献[10]的研究，对于开菱形孔钢板墙，蝴蝶杆的宽厚比越大，蝶形带厚实性越差，也越易发生面外失稳。 本文考虑到开孔对钢板承载力的削弱，控制横向耗能段的高度h，仅改变其宽厚比α，建立HS 系列以研究其对钢板性能的影响。

由图5 钢板的应力云图可知，试件宽厚比α 越大，在层间位移角5%时横向蝴蝶杆面外扭转越严重，因而图6 给出的滞回曲线的形状越向“梭形”靠拢。 由图7（b）HS 系列的骨架曲线以及图11（b）HS 系列各试件的割线刚度可知，Base 试件的承载力和初始刚度最低，而当提高试件的宽厚比α 时，其承载力和初始刚度略微提高。试件HS3 的α 最大为17.1，因此在HS 系列其承载力和初始刚度最高。上述分析再次验证横向蝴蝶杆宽厚比同样对试件承载力和初始刚度的影响较小。 从图11（b）还可以看出：HS 系列横向蝴蝶干的宽厚比较其他系列有所增加，相对而言其厚实性降低，在加载过程中，横向蝴蝶杆更易于发生面外变形，导致其承载力在加载中后期有略微降低，因而刚度退化也随着宽厚比的增加更加明显。

图10（b）是HS 系列各试件的平均能量耗散系数，发现层间位移角2%之前宽厚比较大的试件平均能量耗散系数较高，而2%以后则下降较多，这是因为随着宽厚比的加大，侧移导致的横向蝴蝶杆变形增大，所以试件HS2 和HS3 加载前期蝴蝶杆塑性变形程度较大，耗能充分，而到了加载后期，宽厚比较大的蝴蝶杆水平加载时屈曲产生的面外失稳影响更大，面外扭转现象严重，所以出现能量耗散系数降低的现象，且能量耗散系数降低的幅度随宽厚比的增大而提高。

3.3 竖向蝴蝶板数量和尺寸

由设计理念可知竖向蝴蝶板在双向蝴蝶板剪力墙承担主要水平力，因此其参数对钢板整体性能有显著影响。VN 系列改变竖向蝴蝶板数量m、VS1 改变蝴蝶形端部高厚比β 与HN3 进行对比以研究竖向蝴蝶板参数对钢板性能的影响。 图6（c）和图6（d）、图 7（c）和图 7（d），以及图11（c）和图11（d）分别给了 VN 系列和VS 系列各试件滞回曲线、骨架曲线和割线刚度。 由上述各图可知，对于VN 系列，试件VN2 的峰值荷载为362.62 kN，VN1 的峰值荷载为 145.83 kN，两者相差 60%；VN2 初始刚度最高，为 23.04 kN/mm，VN1 初始刚度最低，为8.76 kN/mm，两者相差62%。对于VS 系列，试件VS1 的峰值荷载为241.58 kN，初始刚度为14.71 kN/mm；HN3 的峰值荷载为189.44 kN，初始刚度为11.04 kN/mm，两者都相差22% 。 由以上分析可知：竖向蝴蝶板数量m 和蝴蝶形端部高厚比β 越大，试件承载力和初始刚度越高，且m 对钢板承载力和初始刚度影响较大。 图10（c）和图10（d）则分别为 VN 和 VS 系列试件的平均能量耗散系数，通过对图10（c）各曲线分析发现三条曲线在加载中前期几乎重合，而在加载后期具有较多竖向蝴蝶板的试件耗能略高，说明竖向蝴蝶板在加载前期不参与试件耗能，但在加载后期与横向蝴蝶杆协调耗能；从图10（d）看出两个试件在加载前期曲线重合，到加载后期由于槽钢对钢板面外约束作用降低，钢板产生整体屈曲，而试件VS 竖向蝴蝶板β 较大，整体屈曲效应更明显，所以耗能较试件HN3 大。

4 结论

基于试验利用有限元软件Abaqus 对双向蝴蝶形钢板剪力墙进行对比验证和滞回模拟，分析了不同几何参数对其抗震性能的影响，得到以下结论：

（1）建立的双向蝴蝶形钢板剪力墙非线性有限元分析在整体变形、横向蝴蝶杆屈曲、滞回以及骨架曲线等方面能与试验结果较好吻合，验证了模型的合理性。（2）除试件HN3、HN4 以及VN1，各系列试件均有较好的抗震性能，较高的承载力和初始刚度，滞回曲线饱满呈现菱形。 通过数值分析可知：各试件均实现了双向蝴蝶板设计理念：在整个加载过程中，竖向蝴蝶板承担大部分水平力，水平蝴蝶杆通过变形协调在加载中前期耗散能量，而在加载后期与竖向蝴蝶板协调耗能，进一步提高构件的耗能行为。 （3）横向蝴蝶杆行数n 增大时，双向蝴蝶形钢板剪力墙的承载力和初始刚度略微提高，但滞回环趋向愈加饱满，试件总耗能量大幅增大。 （4）横向蝴蝶杆宽厚比α 增大时，试件承载力和初始刚度也仅有小幅提高；但蝴蝶杆厚实性变差，侧移中易发生面外失稳，因此试件在加载中前期耗能优异，但加载后期由于蝴蝶杆面外变形较大，能量耗散系数有些许降低。 （5）竖向蝴蝶板数量m 增大时，其承载力、初始刚度和总耗能量增大，钢板能量耗散系数在加载后期也有不同程度增加；竖向蝴蝶板端部高厚比β 增大时，试件承载力和增大程度较高但总耗能量增长有限，因为加载后期竖向蝴蝶板因厚实性变差而更容易发生面外失稳，这也导致能量耗散系数在加载后期因为面外变形的发展而有小幅降低。