预制柱-叠合梁装配整体式框架边节点抗火性能研究

陈 锋， 毛小勇

（苏州科技大学 江苏省结构工程重点实验室， 江苏 苏州 215011）

对于框架结构来说，单个构件的抗火性能往往不能代表整个结构的耐火性能，节点抗火性能对结构整体抗火性能有着十分重要的影响。 在装配式结构中，节点是梁柱等预制构件连接的枢纽，与现浇框架相比有诸多不同，例如装配式节点存在预制构件和后浇区的连接界面，以及装配式节点需要考虑套筒及灌浆料的高温性能等。 因此开展装配式结构节点抗火性能研究具有工程应用价值。

目前对钢筋混凝土及组合结构框架节点抗火性能已有一定程度研究。 王广勇等[1]对钢筋混凝土梁-柱节点耐火性能进行了数值模拟；傅传国等[2]对钢筋混凝土梁-柱节点耐火性能进行了试验研究，在此基础上深入分析了火灾下钢筋混凝土框架节点变形、内力分布、耐火极限和破坏形态等规律。 宋天诣等[3]对钢管混凝土柱-钢混凝土组合梁节点、型钢混凝土柱-型钢混凝土梁节点升降温条件下温度场分布规律进行了有限元模拟和试验研究。Han 等[4]对型钢混凝土梁柱节点进行了试验研究，并给出了节点耐火极限的实用计算方法。然而对装配式框架节点的抗火性能研究还报导不多。

本文利用ABQUS 软件建立预制柱-叠合梁装配整体式框架边节点热-力耦合有限元模型， 对其抗火性能进行理论分析，并与试验结果对比，在此基础上讨论了梁端荷载比、梁纵筋配筋率、梁柱线刚度比值对于装配式边节点耐火性能的影响，分析结果可为装配式节点抗火设计提供参考。

1 有限元模型简介

分析采用ABQUS 的顺序热-力耦合法，首先对节点进行传热分析，然后将温度场计算结果作为内参数导入力学分析中。

1.1 高温下材料性能及参数

混凝土采用“Concrete damaged plasticity”模型，应力-应变关系选用TT-lie 模型[5]。 该模型考虑了混凝土的高温徐变，能较好地反应混凝土高温下力学性能，并且有良好的收敛性。 热膨胀系数、热传导系数、比热选用Lie 给出的公式，密度取2 400 kg/m3，泊松比取0.2。

钢筋采用弹塑性模型，应力-应变关系选用EC3 的模型[6]。 热膨胀系数、热传导系数、比热选用EC3 给出的公式，密度取7 850 kg/m3，泊松比取0.3。

1.2 边界条件

温度场分析中，边界条件为热辐射和热对流，对流和综合辐射系数分别取25 W/m2·K 和0.5，玻尔兹曼常数取5.67×10-8W/m2·K。力学分析中，柱上端限制平面外运动和水平位移，允许竖直位移和平面内转动。柱下端限制竖直水平位移，允许平面内转动。 梁端限制平面外运动。

1.3 接触面定义

钢筋骨架与混凝土采用“Embedded region”接触，端板与混凝土、座浆层与混凝土、上下柱与核心区采用“Tie”接触，预制梁与后浇区混凝土水平叠合面法向采用硬接触，切向摩擦采用罚函数，摩擦系数1.0。将套筒灌浆连接件简化为一个非线性弹簧，不考虑灌浆连接件的几何缺陷，弹簧具有一定的强度和刚度特征，且随温度的变化而变化，高温下弹簧单元荷载-位移曲线参照文献[7]取值。 预制梁与后浇区混凝土竖直叠合面（与核心区连接处）采用非线性弹簧模拟[8]，不考虑高温下叠合面摩擦系数随温度的变化，将不同温度下弹簧荷载-位移曲线输入“inp”文件中，以此模拟装配式节点竖直叠合面的力学特征。

1.4 节点参数及模型

梁在节点区主要承受负弯矩作用，长度取反弯点以内长度；柱取上下柱反弯点,即上下柱中点之间的部分，节点具体构造及梁、柱热电偶位置见图1。

在进行传热分析时，钢筋采用DC1D2 单元，混凝土和灌浆料采用线性热传导单元DC3D8 单元。 力学分析时钢筋采用空间二次桁架单元T3D2 单元，混凝土和灌浆料采用六面体减缩积分单元C3D8R 单元。 预制柱-叠合梁装配整体式框架边节点有限元模型如图2 所示。

图1 预制柱-叠合梁装配整体式框架边节点示意图

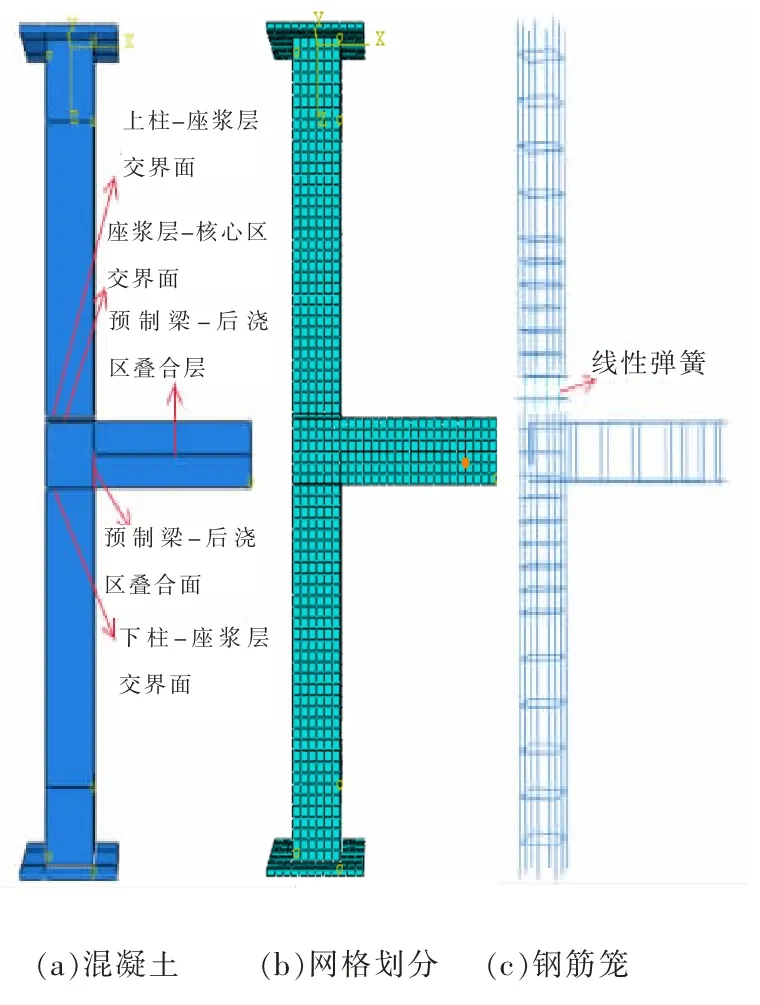
图2 预制柱-叠合梁装配整体式框架边节点有限元模型

2 有限元模型验证

2.1 试件简介

选用课题组在苏州科技大学结构抗火实验室进行的预制柱-叠合梁装配整体式框架边节点抗火试验数据对模型进行验证，试件尺寸如图1，混凝土强度为53 MPa，灌浆料强度为90 MPa，实测直径8 mm 钢筋屈服强度470 MPa，直径12 mm 钢筋屈服强度445 MPa，直径14 mm 钢筋屈服强度445 MPa，直径20 mm 钢筋屈服强度450 MPa，其余参数见表1，试验采用ISO834 标准升温曲线[9]。

表1 试件参数

2.2 温度场对比

梁、柱模拟和实测的各测点温度-时间曲线对比见图3 和图4。 可以看出各点计算温度与实测值发展趋势基本一致，梁截面测点3 温度计算值要略低于试验值。 这主要是由于节点破坏主要发生在梁端，梁端出现裂缝时，热量传入更快，模拟时未考虑裂缝发展。对比梁、柱截面的测点1、测点2 可看出，测点1 温度要高于测点2，这是由于测点1 位于角部，受到两侧传热的影响，而测点2 为一侧传热。 无论是梁截面还是柱截面，实测温度曲线在100 ℃附件出现明显的平台，这是由于混凝土中的水分受热成为水蒸气吸收热量的缘故[10]。

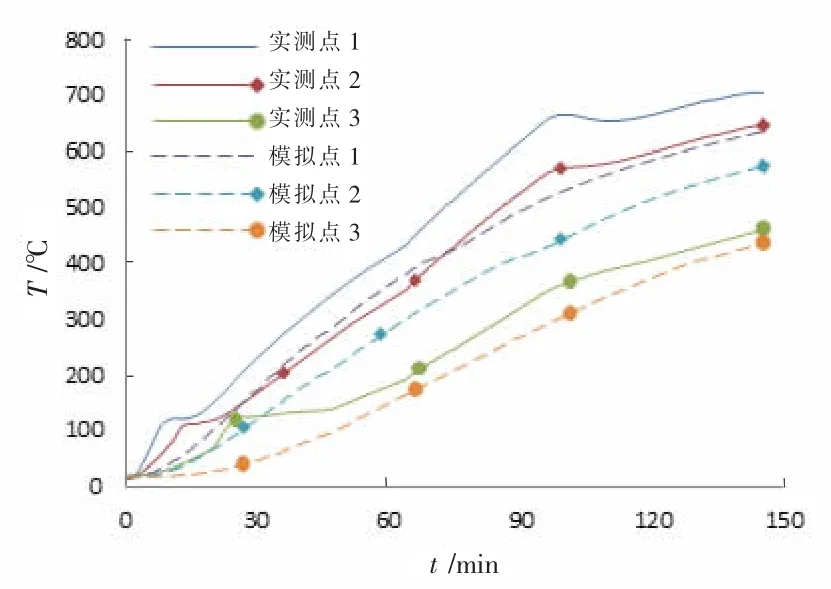
图3 梁截面温度对比图

图4 柱截面温度对比图

2.3 变形曲线及耐火极限对比

梁端位移、柱端位移模拟和实测曲线对比分别见图5、图6，可以看出曲线整体趋势一致。 在起始阶段，梁端位移发展缓慢，在接近耐火极限位移出现陡增；柱端位移先快速上升到最大值，然后平缓下降。 图中模拟值略大于实测值，可能为以下原因：模拟时采用的热膨胀系数与实际有差别；实际受火情况边界条件与模拟采用的不完全一致。

装配式边节点耐火极限取梁端时间-位移出现明显陡增的时间点， 从图5 可以看出实测的耐火极限为145 min，而模拟的耐火极限在135 min，两者误差7%。

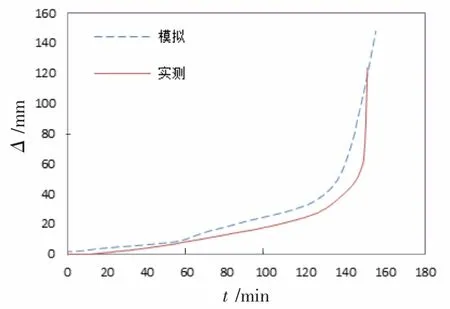
图5 梁端位移对比图

图7 实测裂缝

2.4 破坏形态对比

节点破坏时的裂缝见图7。图8 为计算得到的破坏时节点最大塑性应变分布。 可以看出图8 中拉区塑性最大应变与图7 中裂缝开展位置相吻合。 与现浇节点不一样的是，装配式节点发生破坏时梁现浇区和后浇区交界处产生水平裂缝，这在计算模型中也得到较好体现。 上述温度场、变形、耐火极限和破坏形态的对比表明， 分析模型能较为准确地反应节点抗火情况，可用于预制柱-叠合梁装配整体式框架边节点的高温性能分析。

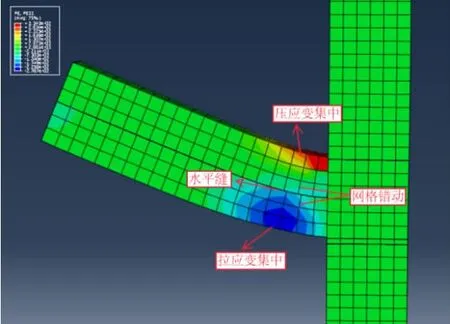
图8 最大主塑应变

3 节点参数分析

3.1 分析参数

主要考虑参数如下：梁端荷载比n，梁纵筋配筋率ρ（ρ=As/bh0），梁柱线刚度比k。 柱端轴压比为0.5，柱截面尺寸300 mm ×300 mm。 考虑三种参数变化，共设计了7 个分析模型，具体参数见表2。

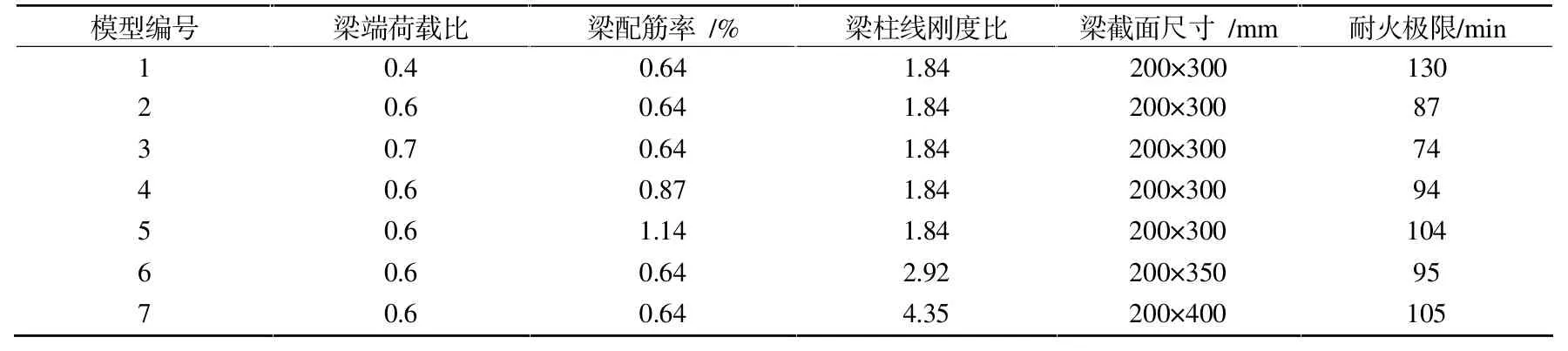
表2 模型参数

3.2 各参数对变形影响规律

不同梁端荷载比条件下，预制柱-叠合梁装配整体式框架边节点的梁端时间-位移曲线如图9 所示。 可以看到，随着荷载比n 的增大，时间-位移曲线出现明显拐点的时间要提前。n=0.6 和n=0.7 情况下，曲线在拐点后的趋势接近，但是与n=0.4 情况相比，拐点后荷载-位移曲线更陡，上升速率更快，这说明大荷载比情况下，梁端破坏更加突然。

图10 为配筋率对梁端位移的影响，可见随着配筋率逐渐增大，时间-位移曲线到达明显拐点的时间推迟。三种配筋率情况下，在节点达到耐火极限前，相同受火时间点位移值较为接近。 在到达拐点后，于相同受火时间点，配筋率越大，梁端位移越小。

图11 为梁柱线刚度比k 对梁端位移的影响，可见随着梁柱荷载比增大，时间-位移曲线到达明显拐点的时间略有推迟，曲线走势基本相同。 在相同受火时间点，线刚度比越大，位移越小。

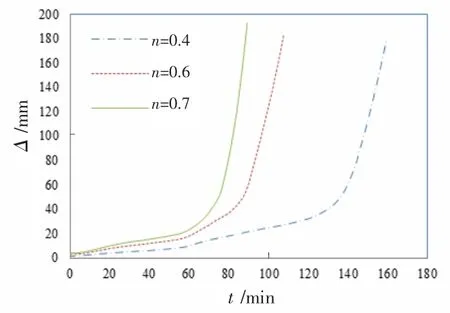
图9 梁端荷载比对梁端位移影响

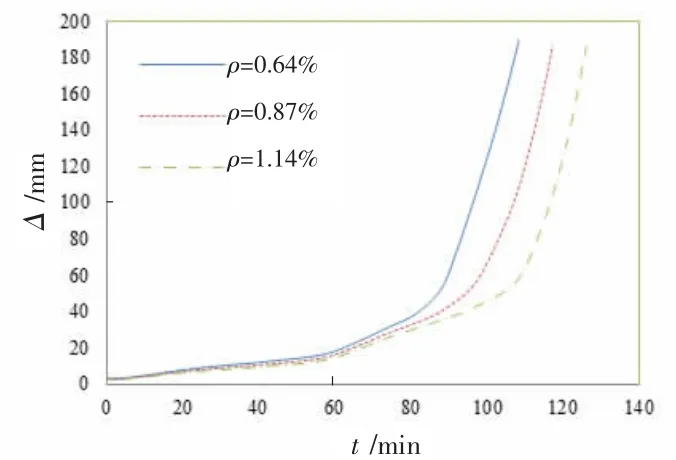
图10 配筋率对梁端位移影响

图11 梁柱线刚度比对梁端位移影响

3.3 各参数对耐火极限影响规律

图12 至图14 分别为梁端荷载比、梁纵筋配筋率、梁柱线刚度比对节点耐火极限的影响曲线。 从趋势上看，随着梁端荷载比的增加，节点耐火极限减小；随着梁纵筋配筋率增大，节点耐火极限增大；随着梁柱线刚度比值增大，节点耐火极限增大。 配筋率和梁柱线刚度比值对节点耐火极限的影响趋势相同，但是与梁端荷载比相比，两者的影响相对较小。

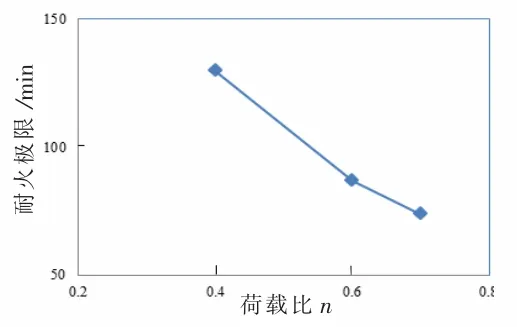
图12 梁端荷载比对边节点耐火极限影响

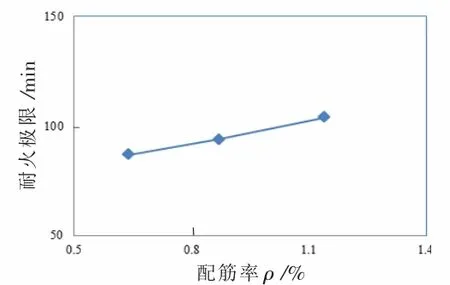
图13 配筋率对边节点耐火极限影响

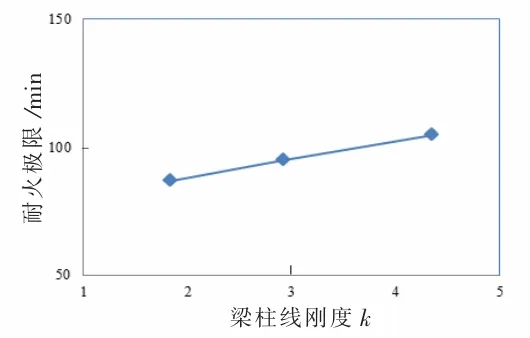
图14 梁柱线刚度比对边节点耐火极限影响

4 结论

（1）在强柱弱梁设计情况下，火灾下节点破坏由梁控制。破坏位置在距离节点核心区一段距离处，主要是由于核心区处温度较低，对连接的梁有一定保护作用。并且现浇梁和后浇带叠合层位置处出现水平缝。（2）在ISO834 标准升温条件下，预制柱-叠合梁装配整体式框架边节点的梁端时间-位移曲线大体呈先缓慢增长再陡增的趋势，有明显拐点，节点破坏具有一定的突然性。 （3）梁端荷载比越大，耐火极限越小；梁纵筋配筋率、梁柱线刚度比值越大，耐火极限越大。梁端荷载比对节点耐火极限的影响最为显著，而梁纵筋配筋率、梁柱线刚度比值的影响则相对较小。