径向压电驱动液体变焦凹透镜的机理研究

许 珂， 李 华， 茆廷学

（1.苏州科技大学 数理学院，江苏 苏州 215009；2.苏州科技大学 机械工程学院，江苏 苏州 215009）

近年来科学技术的发展十分迅猛，变焦透镜在许多领域有所运用，如手机或者照相机的镜头设备[1]。 传统的光学变焦系统需要大量的透镜做机械运动，不仅成本高，而且工艺复杂。 新型的光学变焦系统不仅不需要做机械运动，而且可以减小体积，适用于更多的领域并且满足了对变焦透镜的精密性和像质越来越高的要求[2]。 因此研究结构简单、紧凑、响应速度快的新型变焦透镜具有十分重要的意义[3]。 液体透镜就是这种新型变焦透镜，大多数液体透镜是利用了电湿润现象，其原理是通过改变液体和绝缘基板之间的电压来改变液滴在基板上的接触角，从而改变焦距[4]，其焦距最小可到50 mm。 此外，可以通过改变液体的折射率，使折射率产生梯度变化来实现变焦，如液晶变焦透镜[5]，这种变焦透镜由于材料特性限制焦距最小可到10 cm。还可以对腔体内液体加压，改变腔体内的液体分布，改变腔体表面透明弹性薄膜或物质自身表面的曲率半径，从而实现焦距改变[6]，此透镜虽然焦距变化范围很广，但有响应速度慢和体积较大等缺点。 本文研究的是一种径向压电驱动液体变焦透镜的变焦机理，圆环压电陶瓷的径向振动会使内腔中产生压强，当液体分界面中声波的反射压强呈一定规律分布时，液体表面发生形变，透镜的焦距发生变化。

1 驱动机理分析

1.1 透镜结构

本文设计的变焦透镜结构如图1 所示。 中心位置是一个环形压电陶瓷片，材料选用较高灵敏度、机械激励振幅大，机械损耗低且介电损耗低[7]的PZT4。硅胶的热稳定性好，粘滞系数比水溶液大，可以最大限度降低温度对透镜的影响，所以空腔中的液体选择硅胶。 圆环压电陶瓷底部用耐高温的环氧树脂胶粘连PET 圆形薄膜，上表面硅胶直接接触空气。 在PZT 圆环镀银的上下表面焊接两根金属丝作为电极，在两个电极间施加一定频率的超声电源驱动使圆环压电陶瓷径向振动。 此时透镜内有不同分布的压强，硅胶表面发生形变，透镜的焦距发生变化。

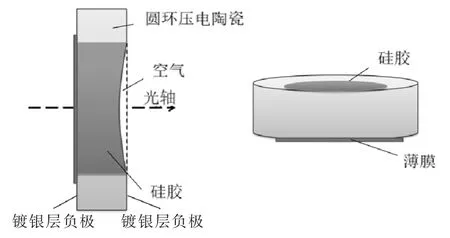
图1 透镜结构

1.2 径向振动压强分析

令圆环压电陶瓷高度为d，内径为a1，外径为a2，并设圆环压电陶瓷的中心为坐标原点，圆环中心轴线为z 轴，与圆环底面平行的面为XOY 平面，见图2。由于压电陶瓷圆环为径向振动，将压电陶瓷圆环分成无限多个微小体元，每一个微小体元可看作一个点声源[8]。 这里的点声源并不是传统的球形点声源，是一种有固定振动方向的声源，振动方向沿X 轴径向传播。

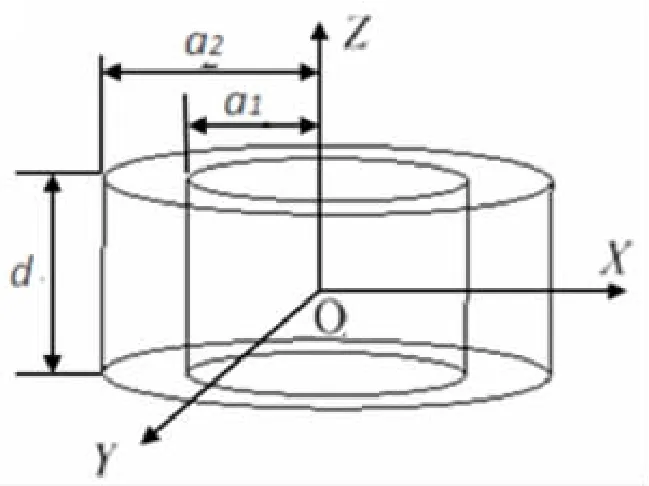
图2 圆环径向辐射声源

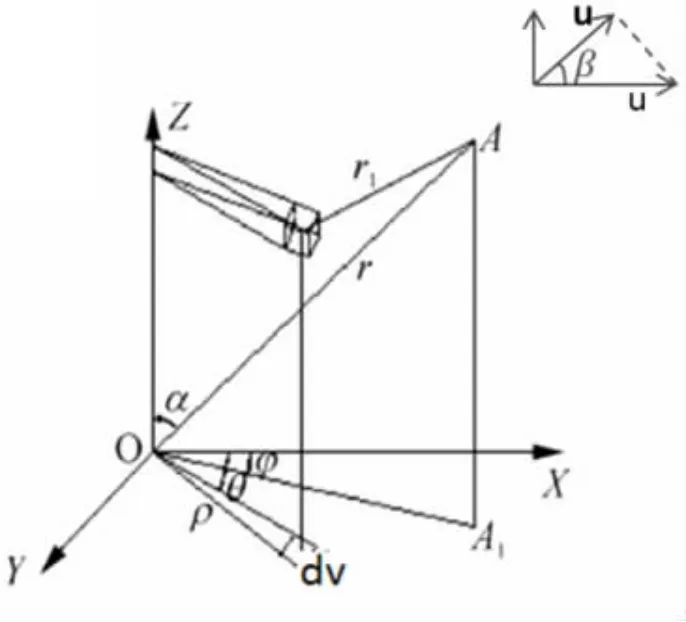
图3 解析模型图

在坐标系中，任一点A 位于距离坐标原点r，与z 轴夹角α。 点A1为点A 在XOY 面内投影，与X 轴夹角为φ。在圆环上任取一微小面元dv，其空间位置高为d，在XOY 面上的投影dv 的极径为ρ，极角为θ，见图3。则dv 在观察点A 处产生的压强为[9]

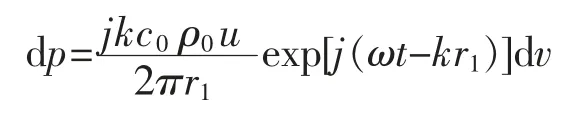
式中，k 为波数；c0为波速；ρ0为介质静态密度；u 为声源的振速；ω 为圆环谐振频率；t 为时间。 根据图3 得到由于振速u 的实际方向是沿X 轴方向，要将u 分解成点源到观察点A 的方向，并且所求为垂直方向上的压强分布，所以要再次分解，如图3 所示，即u=ucosβ。 对式（1）积分pi为入射压强：

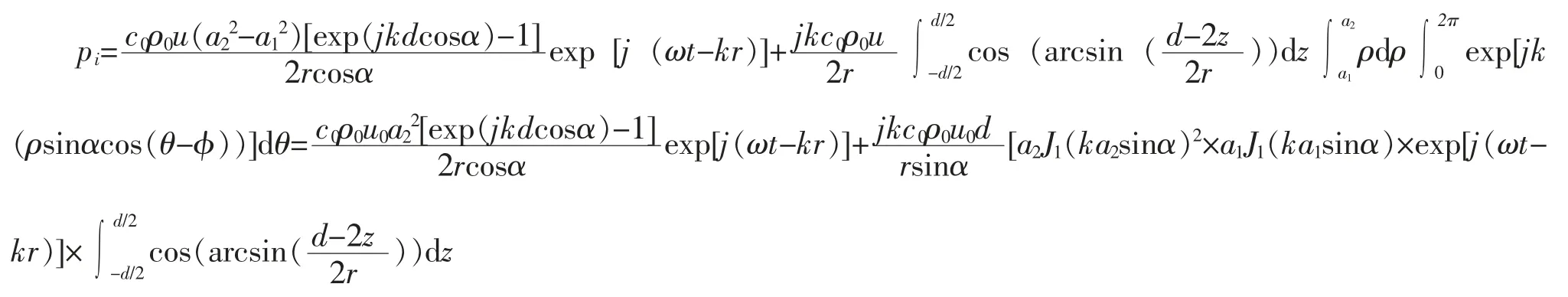
1.3 分界面压强分析

由于声波在两种阻抗不同的介质的分界面上会发生反射和折射，这时就会有反射压强和折射压强产生。而硅胶和空气都是流体，反射波和折射波中只有纵波没有横波。

根据斯奈尔声波反射和折射定律，可知声波遇到分界面时，反射角等于入射角，则折射波压强与入射波压强之比为

其中，zs2、zs1分别为入射波和折射波压强与相应质点速度法向分量的比值[10]，pt为折射压强。 在第一介质中声压p1=pi+pr在第二介质中声压p2=pt并且在分界面处z=0 满足边界条件：（1）声压的连续性即p1=p2；（2）法线振速连续即

由边界条件可知分界面上受到的力也是连续的，第一介质中受到的力为入射压强与反射压强的和，第二介质中受到的力为折射压强，这两个力大小相等方向相同，方向为硅胶-空气。 透镜的表面形状由折射压强决定，且透镜的形貌与折射压强大小分布相同。

图4 为分界面上任一直径上的折射压强分布，原点为圆环压电陶瓷的圆心，原点折射压强最小，且随着半径的增大折射压强增大，当增大到最大值时又会随着半径的增大而减小。

圆环压电陶径向振动产生不同分布的压强，在硅胶和空气的分界面声波会发生反射和折射，分界面的总压力为折射压强，径向振动液体透镜的表面形状由折射压强的大小决定，压强大的地方形变比较明显，压强小的地方形变不明显，分界面表面凹陷，所以理论分析该液体透镜为凹透镜。

2 试验研究

为验证理论分析的结果，搭建了试验平台，测试了圆环压电陶瓷的径向振动，分界面的压强分布和透镜表面形状，为了进一步测试透镜效果，还做了透镜成像实验。

2.1 试验条件及系统

制作了径向压电驱动液体变焦透镜，由15 mm×6 mm×3 mm 圆环压电陶瓷、0.7 mm 厚PET 薄膜和3 mm高硅胶（型号：hs-200 配比：1∶14）组成。 搭建液体透镜的试验系统见图5，试验仪器参数情况如表1 所列。

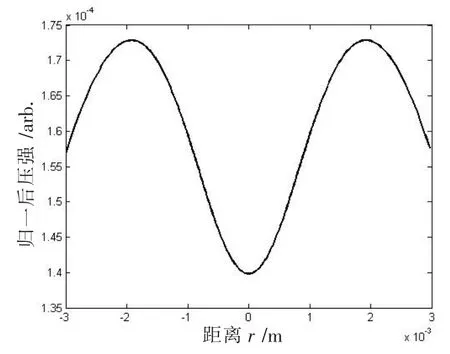
图4 分界面折射压强分布

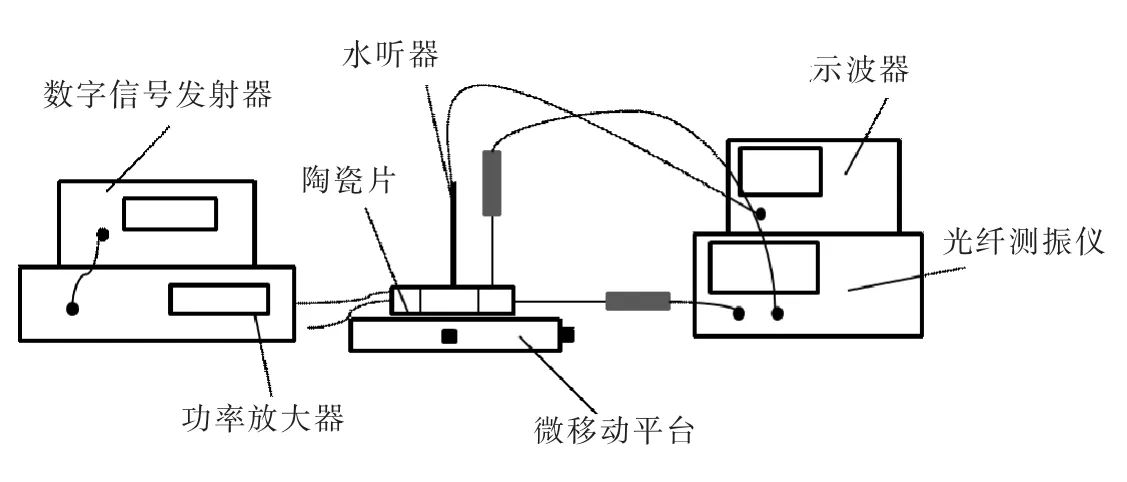
图5 液体透镜试验系统

2.2 压电陶瓷的振动测试与仿真

用阻抗分析仪检测分析组装好的液体透镜， 测试得到了液体透镜径振模态的谐振频率是99 451 Hz。运用光纤测振仪可以测量高频振动的位移， 测试压电振子厚度方向和径向方向的位移就可以确定圆环压电陶瓷的振动方式，试验结果见图6。

表1 试验仪器型号参数

在100 145 Hz 时，随着驱动电压的增大，圆环压电陶瓷径向方向振动增大并且厚度方向振动几乎保持不变， 所以压电陶瓷的振动方式是径向振动。并且在示波器中显示上下表面的振动相位相同，符合径振的特征。

利用有限元分析软件ANSYS，根据圆环压电陶瓷的尺寸和参数，建立了有限元分析模型，得到了径向振动的模态分析图，如图7 所示。 从图中可以看出圆环压电陶瓷厚度方向没有振动，径向方向振动明显，此时谐振频率为98 780 Hz，仿真与试验结果相一致。

图6 厚度和径向方向位移随电压的变化

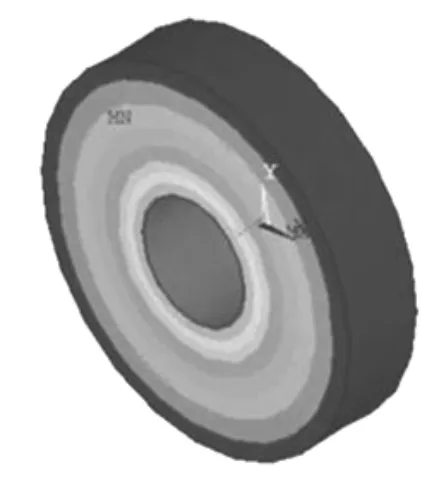
图7 压电陶瓷模态分析

2.3 压强分布试验

利用灵敏度0.145 mV/Pa 探针式水听器作为传感器，测量硅胶表面沿径向方向上的压强。 压强传感器连接示波器， 圆环压电陶瓷连接数字信号发生器和功率放大器，微移动平台控制距离。分别在输入电压为40、60、70、80 和120 V 时， 使用传感器距离底面薄膜3 mm 处即探针式水听器接触硅胶表面，并且水听器的侧面接触到圆环压电陶瓷内径，沿着圆环径向方向移动微移动平台，每隔0.5 mm 测量一次，多次测量不同径向方向上的压强并取平均值，结果如图8 所示。

原点即圆环压电陶瓷中心压强最小， 输入电压40、60、70、80 和120 V 都随着距离圆心的距离增大压强增大，增大到2 mm 处时压强减小，与理论推导一致。 并且随着输入电压的增大压强增大，当输入电压增大到80 V 后压强几乎不变。

图8 不同径向方向的压强分布

2.4 透镜表面形状试验

将制作好的圆环压电陶瓷变焦透镜放置在平台上，使用光纤位移传感测量硅胶表面任一直径上的位移变化。 将透镜连接数字信号发生器和功率放大器，频率选择99 823 Hz，当电压为0 V 时，硅胶液面静止不动，由于表面张力的存在不是完全水平的，使用光纤位移传感器在压电陶瓷圆环内径上任一反光点测量位移，用微移动平台控制距离，在一条直径上每移动0.5 mm 测量一次，即可表示在0 V 时一条直径的硅胶表面形状。 逐渐增大电压，硅胶液面凹陷程度越大，当电压为40、60、70、80 和120 V 重复上述试验步骤，即可得到在40、60、70、80 和120 V 时一条直径上的硅胶表面形状，和0 V 位移的差值就是改变电压变焦透镜表面实际发生的变化，如图9 所示。

从图9 中可以看出，原点发生形变最大，且随着半径的增大形变减小，为凹透镜。 当电压增大时透镜形变也增大，到80 V 后形变量几乎不变。用MATLAB 软件对40 V 时的曲线进行拟合，由于不同直径上的形变几乎相同，所以将拟合后的曲线绕Z 轴旋转，得到一个三维图像（见图10），可以清晰看出透镜为凹透镜。

图9 透镜表面位移变化

图10 表面情况三维图

2.5 透镜的成像试验

搭建一个物距2.5 mm，像距295 mm 的光学平台，如图11 所示。 改变透镜的输入电压， 拍摄各个输入电压下像的情况， 通过MATLAB 图像处理的方法得到变焦透镜的放大率， 使用高斯公式计算得到变焦透镜在不同电压下的焦距，如图12 所示。 两条曲线分别代表水平方向和竖直方向的焦距，随着电压的增大，超声驱动变焦透镜的焦距的绝对值减小，其焦距范围为-10 mm 到-90 mm。在电压20 V 至80 V 时焦距变化比较明显，电压80 V 后焦距几乎不变，与声压试验和透镜表面形变试验结果相同。 水平方向和竖直方向的焦距没有完全重合表明有畸变存在。

图11 试验平台

3 结语

研究表明，径向压电驱动的液体变焦透镜的机理为径向振动的圆环压电陶瓷中产生不同分布的压强使透镜焦距发生变化。 试验证明该透镜为凹透镜，透镜中心压强最小，随着半径的增大压强增大；透镜中心形变量最大，随着透镜半径的增大形变量减小；输入电压不同焦距不同，输入电压越大焦距越大，焦距的变焦范围为-90 mm 到-10 mm。 结果表明理论分析和试验结果相一致。

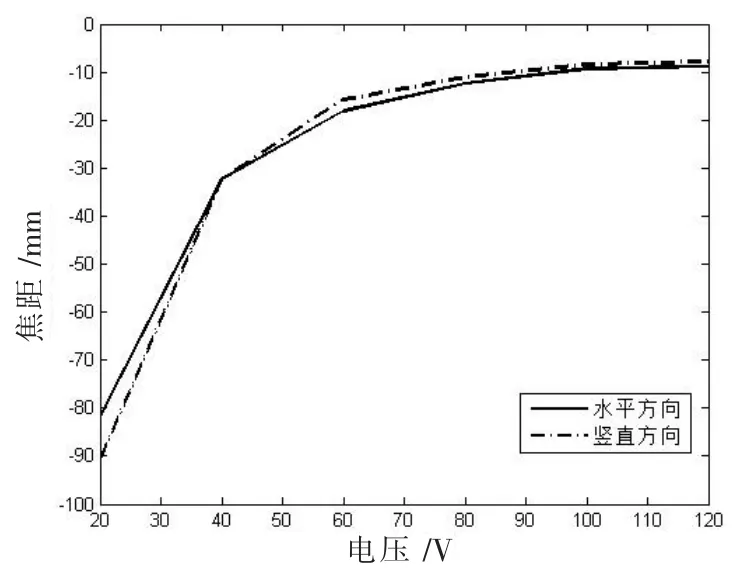
图12 不同电压下的透镜焦距