基于排队论模型的公共自行车站点车辆调度数研究
李 军, 朱从坤
(苏州科技大学 土木工程学院,江苏 苏州215011)
近年来,公共自行车作为政府大力推行的绿色低碳出行方式,被广泛应用于各大城市。 然而,在日常运营过程中,公共自行车站点经常出“空桩”或“满桩”现象,严重影响了市民使用公共自行车的满意程度和公共自行车使用效率。产生这一问题的原因之一,是由于站点车辆调度不及时造成的。关于公共自行车的调度问题,马智超等针对计算出每次派出的调度车数和最优路线的问题,基于改进的混合智能水滴算法,提出了一种的融合策略数学模型[1]。刘冉等结合库存与车辆路径规划建立了库存-路径模型,利用遗传算法求解调度量与路径的多种组合方案[2]。 张辉等通过分析公共自行车调度方式特性,提出了一种带模糊时间窗的城市公共自行车调度路径优化模型,同时基于蚁群算法求解最优调度路径模型[3]。 可以看出,关于公共自行车调度已有很多方法:水滴算法、遗传算法和蚁群算法等等。
排队论作为一种比较成熟的理论,被广泛应用于分析交通系统中的一些排队现象。 例如周智勇等引入排队论原理建立了出行过程中的车辆停放接受条件概率模型[4];殷月竹等运用排队论和Poisson 过程对公共停车场的停车情况进行分析,并建立排队论模型[5];程林结等采用排队论的方法对停车场规模在给定车辆损失率的前提下,求出满足条件的最佳服务窗口数[6]。 这些研究很好地解决了车辆停放管理中的一些问题。
本文期望通过新的方法来解决公共自行车调度车辆数问题。 在公共自行车站点处,市民借、还公共自行车的过程可以看作是一种排队现象,利用排队理论,通过分析站点的顾客损失,得出站点在快要“满桩”或“空桩”时需调配的最优车数,由此可为公共自行车的及时调度提供一定的指导依据。
1 公共自行车站点排队系统描述
1.1 排队系统假设
假设公共自行车站点的服务为一个排队系统,需要满足两个条件:一是站点提供的服务时间是随机的;二是提供的服务是确实存在的。 由于到达站点的顾客为还车和借车两类,因此需将站点排队系统分为两种,即还车排队,以及借车排队。
(1)顾客还车排队。 对于公共自行车站点而言,此时将空闲公共自行车桩视为服务台,服务时间为车辆在车桩上的停放时长,则服务效率为车桩周转率[7]。 当一个还车顾客在公共自行车站点停放车辆以后,由于顾客借车的时间是不确定的,取决于借车顾客出行需求,所以公共自行车在车桩处所停留的时间长短是随机的,即公共自行车桩的服务时间是随机的。
(2)顾客借车排队。 对于某个公共自行车站点,此时将每一辆可借公共自行车看作一个服务台,可借公共自行车的服务时间是公共自行车的使用时长,则服务效率为公共自行车周转率[8]。 当一个借车顾客在公共自行车站点借到公共自行车以后,由于借车顾客到达目标站点的距离是不同的,所以每个顾客使用公共自行车的时间是随机的,即公共自行车对借车顾客的服务时间是随机的。
1.2 输入过程
无论对于还车顾客或是借车顾客而言,顾客源都是独立、源源不断且随机地到达公共自行车站点接受停放服务或租借服务的,且互不影响。
1.3 排队规则
当还车顾客到达公共自行车站点时,如果站点有空闲车桩便立刻进行还车服务,若站点“满桩”,则还车顾客会选择离开,另寻别处站点停放公共自行车;当借车顾客到达公共自行车站点时,如果站点有可借公共自行车便立刻进行借车服务,若站点“空桩”,则借车顾客会选择离开,另找其他交通出行方式。 即公共自行车站点是先到先服务的损失制随机服务系统。
1.4 服务方式
站点中有K 个相互独立的空闲公共自行车桩(或可借公共自行车),它们之间是相互独立、随机为顾客提供借还车服务的,并且每个空闲公共自行车桩(或可借公共自行车)的服务能力是相同的,每个空闲公共自行车桩(或可借公共自行车)只能同时对一个顾客提供服务。
2 排队系统输入输出分布
为确定公共自行车站点顾客到达及服务时间的分布方式,从永安行科技股份有限公司搜集苏州市高新区部分公共自行车站点2018 年6 月11 日一天的借还信息(站点总计14 个),数据信息包括公共自行车的车号、借出车站、借车时刻、归还车站、还车时刻、用车方式、用车时间、借出站号、借车位、还车站号、还车位等。
公共自行车站点服务对象来自站点周边的人群,车辆借还的时间分布特征与站点周边人群的出行规律密切相关,为此将14 个站点根据所处地位置和服务的主要人群分为六类:工作上班站点、商场商业地区站点、人群集中区站点、住宅小区站点、轨道交通换乘站点、学校附近站点。 每类站点选取一个典型站点进行研究,即金狮大厦站、绿宝广场站、枫津菜场站、马浜花园站、轨交滨河路站、高新区二中站。 详见表1 所列。
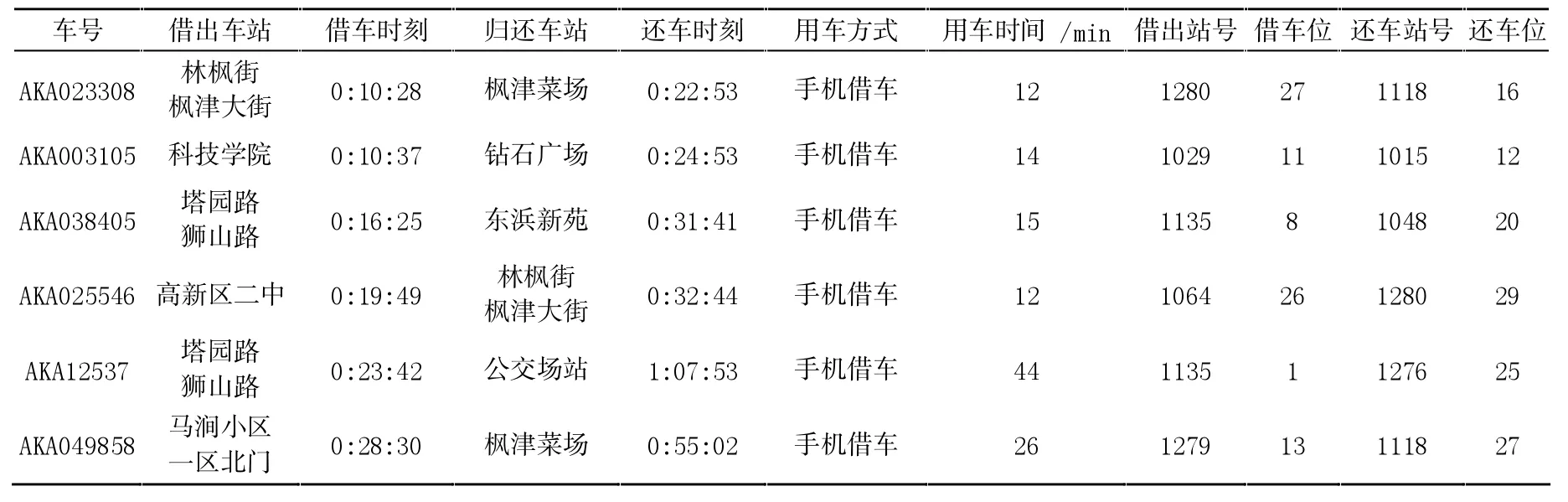
表1 苏州高新区部分公共自行车借还数据(2018 年6 月11 日)
2.1 输入分布
针对某个站点,将到该站点借(还)车的顾客按到达时间进行排序,相邻两顾客到达时刻之差即为其借(还)车时间间隔。 由于站点处顾客的到达具有随机性,顾客借(还)车的时间间隔也不相同,以1 min 为时间步距,对一天中不同借(还)车时间间隔发生次数进行统计;其中金狮大厦站点的统计结果见表2 所列。
依据表2 中数据,绘制借还车时间间隔频数分布曲线,如图1 所示。 由图1 可以看出,金狮大厦站的车辆借还时间间隔基本服从负指数分布。将数据输入matlab 软件,利用cftool 工具箱,进行负指数分布拟合及优度检验,结果如图2 与图3 所示。
(1)漏浆处理。成槽过程中,对固壁泥浆漏失量及泥浆净化回收量作详细测试和记录,如漏浆量不大,可采用加大泥浆浓度或增投堵漏剂等措施进行处理,若漏浆量过大,应适当放缓铣进速度,同时往槽孔中投放堵漏材料或在槽底灌注纯水泥浆的方式进行处理,待槽孔内泥浆恢复正常后再恢复正常施工。
由检验结果可知, 金狮大厦站的借还时间间隔频数分布拟合优度R-square 都大于0.95。其余五个站点的优度检验结果见表3。由此可知,公共自行车站点借、还车时间间隔均服从负指数分布。
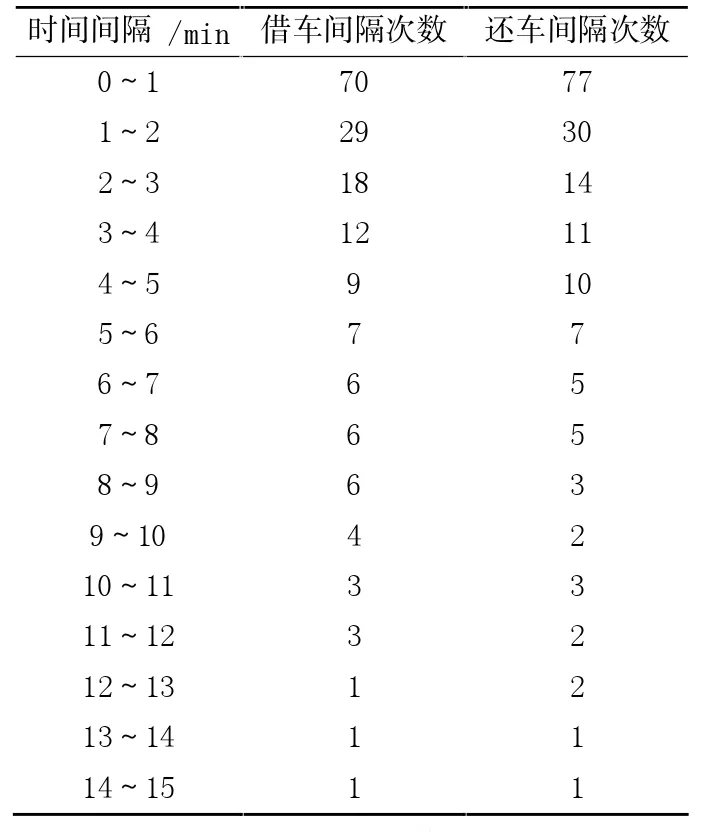
表2 金狮大厦站借还车时间间隔次数
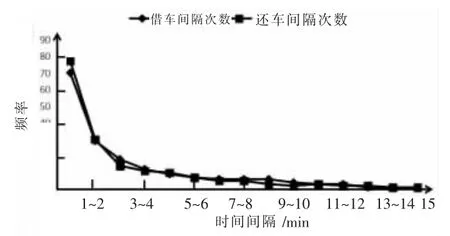
图1 金狮大厦站借还时间间隔分布曲线
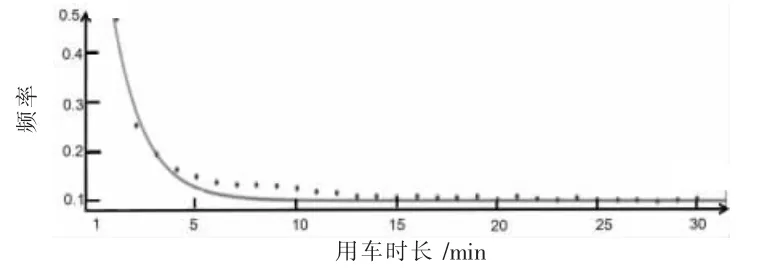
图2 金狮大厦站借车负指数分布拟合图

图3 金狮大厦站还车负指数分布拟合图

表3 各站点负指数分布检验结果统计
2.2 输出分布
2.2.1 用车时长分布 对于站点的借车排队系统,每辆公共自行车被使用时间即为一个服务台的服务时间。由于异地还车机制,公共自行车从A 站点借走,在B 站点还车,用车时长的随机性与站点属性无关,只与借车顾客的使用有关,那么对于用车时长,不必区分公共自行车站点类型。 定义用车时长为公共自行车从A 站点借走直到在B 站点归还期间耗费的时间,将表1 中用车时间数据进行频数统计,其分布图如图4 所示。 利用matlab 软件,对用车时间频数统计数据进行负指数分布拟合,结果如图5 所示。 可知公共自行车用车时长的拟合优度R-square 为0.954 3,属于拟合非常良好,是符合负指数分布的。

图4 公共自行车使用时长频数分布图

图5 用车时长负指数分布拟合图
2.2.2 停车时长分布 对于站点的还车排队系统,服务时间为车辆在车桩上停放的时长。 在所搜集的车辆信息中,每辆公共自行车都有对应的编号,停车时长就是对应编号的公共自行车在同一站点借、还时刻的差值。 对不同的停车时长出现的频数进行统计,如图6 所示;对其进行负指数分布拟合,结果见图7。 拟合检验结果显示,公共自行车停车时长即车桩服务时间的拟合优度R-square 为0.945 5,服从负指数分布。
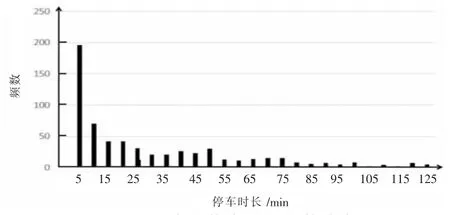
图6 车桩停车时长频数分布图

图7 停车时长负指数分布拟合图
综上,公共自行车站点的排队是M/M/K/∞排队系统。
3 损失制排队系统效率指标
在M/M/K 排队系统中,顾客按负指数输入,平均到达率为λ;服务时间呈负指数分布,服务率为μ;单个车桩或公共自行车服务强度ρ=λ/μ。 有k 个车桩,先到先服务,顾客源无限。 若还车时为“满桩”,或借车时为“空桩”,顾客则离开。 损失制排队系统基本效率指标为[9]

式中,参数分为两种情况:
(1)还车排队系统,此时WS为还车顾客在系统中停留时间的期望值,min;P0为没有顾客前来还车的概率;Ls为站点剩余平均空桩数量,个;Pn为站点有n 个空闲公共自行车桩可供停车时的顾客损失率。
(2)借车排队系统,此时WS为借车顾客在系统中停留时间的期望值,min;P0为没有顾客前来借车的概率;Ls为站点停放的平均可借公共自行车数,辆;Pn为站点有n 辆公共自行车可借时的顾客损失率。
4 站点最优车辆数模型
公式(1)中Pn为站点有n 辆可借公共自行车或n 个空车桩时借、还车顾客的损失率,以站点损失率不超过5%为约束条件,通过约束条件可计算出最优化的公共自行车调度数量或预留空车桩数量。 假设参数a 是最优化的空闲停车桩(或可借公共自行车)数量,则[10]:

将 P0代入 Pa可得

5 站点调度实例分析
5.1 站点公共自行车数时变曲线
对某一公共自行车站点,若已知其初始在桩车辆数,则可根据实时车辆借还信息,采取“借车为减,还车为加”绘制出站点车辆数时间变化曲线。如果站点实时车辆数超过停车桩数量,则“无桩可停”,会损失还车顾客;如果站点实时车辆数变为负数,则“无车可借”,会损失借车顾客。 以金狮大厦站为例,假设其站点初始车辆数,根据实时数据绘制车辆的时变曲线如图8、图9 所示。
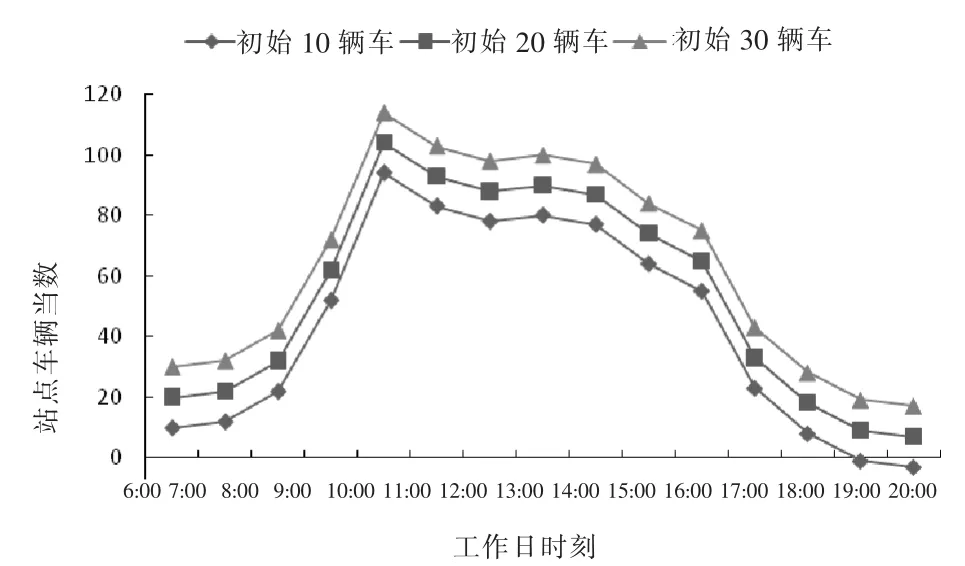
图8 金狮大厦站工作日车辆时变曲线
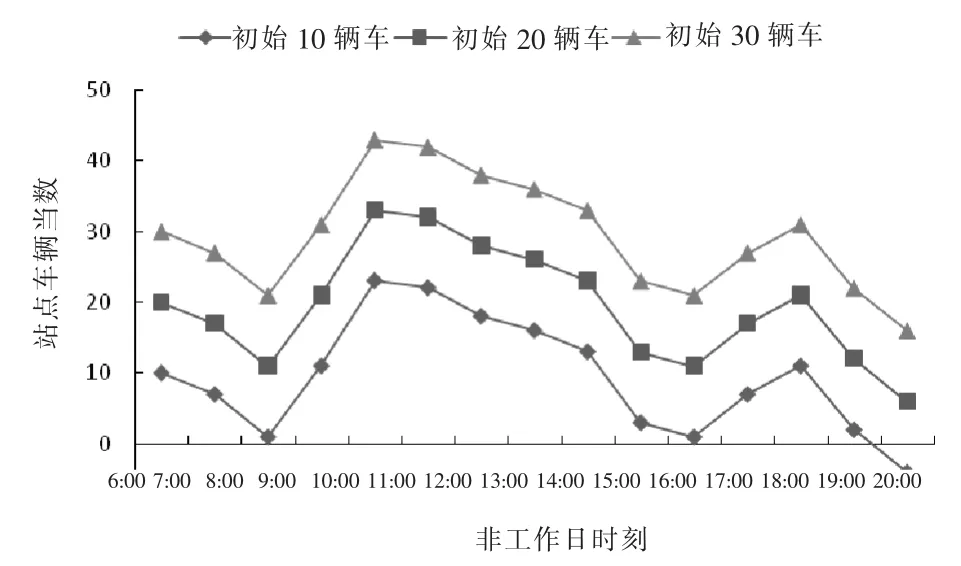
图9 金狮大厦站非工作日车辆时变曲线
金狮大厦站点有40 个停车桩,由工作日(2018 年6 月11 日)的车辆时变曲线可知,从8:00 左右开始,公共自行车的数量持续超过40 辆, 这说明早上八点左右开始的早高峰时期前来还车的顾客多于借车顾客,若不及时调走车辆,会造成无桩可停。从18:00 开始,公共自行车数量接近于0,说明在晚六点前的晚高峰期内,前来借车的顾客多于还车顾客,如不及时调入车辆,会造成无车可借。
在非工作日(2018 年6 月16 日),金狮大厦站的实时车辆数没有超过40 辆,说明站点在保证有20 辆左右初始车辆数的情况下,站点本身的顾客借还量趋于平衡,全天无需进行车辆调度。
5.2 调度公共自行车数计算
在工作日,金狮大厦站点早高峰期间需调出车辆,留出足够多的空车桩以满足还车需要;晚高峰期间需调入一定数量的车辆,以满足借车需要。 利用公式(6)可求得顾客损失率小于5%的车辆调配数或空桩数。
对于早高峰,计算早高峰期间还车顾客到达的平均还车时间间隔,其倒数即为还车顾客的平均到达率,λ早还=78 辆/h,车辆在车桩上平均停放时长的倒数即为平均服务率 μ平均=4.178 辆/h。 利用式(6)计算不同空桩数时的顾客损失率,如表4 所示。 可知,当空车桩数为24 个时,还车顾客损失率为4.5%,说明在早高峰期间,站点车桩快“满桩”时,应调度车辆留出24 个空桩位。
对于晚高峰,计算晚高峰期间借车顾客到达的平均时间间隔,其倒数即为借车顾客的平均到达率,可示为 λ晚借=110 人/h;顾客平均用车时长的倒数即为平均服务率,μ平均=7.012 6 辆/h。利用式(6)计算不同公共自行车数时的顾客损失率, 如表5 所列。 由表5 可知, 当可借公共自行车数为21 辆时, 借车顾客损失率为4.2%,说明在晚高峰期间,站点车桩快“空桩”时,应调度车辆使站点有21 辆可借公共自行车。

表4 金狮大厦站早高峰还车顾客损失率计算表

表5 金狮大厦站晚高峰借车顾客损失率计算表
综上所述,金狮大厦站点在早高峰快“满桩”时,应调出公共自行车,预留24 个空车桩位以供还车;在晚高峰快“空桩”时,应调度21 辆公共自行车以供借车。 以保证公共自行车借还车顾客的损失率在5%以下,满足了绝大多数借还车顾客的需求,有利于提高公共自行车服务水平。
6 结语
为更好的发挥公共自行车的作用,提高公共自行车站点服务水平,针对公共自行车车辆调度数量问题,在分析站点顾客到达规律、车辆使用时长及停放时长规律的基础上,建立基于排队论的公共自行车站点车辆调度数量优化模型,以借还车顾客损失率小于5%为约束条件,将模型应用于苏州市高新区金狮大厦站点,计算了该站点在早晚高峰时段内较为合理的公共自行车调度数量,为公共自行车运营管理提供指导意见。
——金狮狨
——金狮面狨

