均质土坝正交各向异性渗流场数值模拟

孙旭曙，梁佳灯，陈 超，左小鹏，郭晓萍

（三峡大学 水利与环境学院，湖北 宜昌443002）

1 引言

土石坝受填筑材料颗粒含量比例、颗粒级配、施工方法等因素的影响，使其颗粒在不同方向上的排列不同，进而在力学特性、力学参数等方面产生差异［1］，在宏观上表现出非均质性和各向异性。 由于土石坝坝体填筑材料渗透特性在水平向和竖直向相差较大， 导致实际工程中存在坝体实测浸润线高于计算值、渗流量增加、渗透比降加大等问题。 基于上述原因，在SL274—2001《碾压式土石坝设计规范》中规定［2］，土石坝渗流计算应考虑坝体和坝基渗透系数的各向异性。

深厚覆盖层坝基地层的天然沉积和坝体的分层填筑、碾压，使得坝基和坝体在渗透特性上表现为各向异性，进而影响其渗流场的分布。 邱珍锋［3］基于室内试验研究了砂泥岩颗粒含量比例、颗粒级配、试样干密度等因素对砂泥岩颗粒混合料渗透各向异性特性的影响， 阐述了砂泥岩混合料试样各向异性渗透特性的机理。 胡瑞［4］考虑了材料渗透参数的各向异性特性，开展了土石坝饱和-非饱和渗流分析；漆力健［5］研究了各向异性渗流情况下边界条件选取对渗流场的影响， 并将渗流边界条件概化为四类数学模型；何秉顺［6］考虑堤坝非饱和区土体水平渗透能力大于垂直渗透能力，研究表明堤坝内浸润线升高，水头等势线越倾斜，相应点处的孔隙水压力却会降低；罗胜平［7］采用数值模拟研究了各向异性土坝在4种排水体条件下的坝体渗流特性， 研究表明坝体的排水效果与坝体各向异性渗透特性密切相关。

本文以均质土坝为研究对象， 采用数值模拟方法研究了稳定渗流条件下坝体填筑材料各向异性渗透特性对坝体渗流场分布的影响， 重点分析了坝体浸润线、下游坝坡出逸点高程、单宽流量、坝体最大渗透比降的变化规律。

2 二维各向异性渗流计算理论

2.1 渗流控制方程

GeoStudio岩土分析软件中，SEEP/W模块的瞬态二维渗流控制方程可表述为［8］：

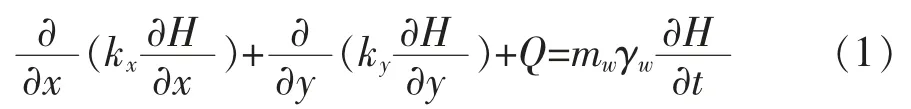
式中 H为总水头（m）；kx为x方向的渗透系数（m/s）；kv为y方向的渗透系数（m/s）；Q为施加的边界流量（m3/s）；t为时间（s）；mw为储水曲线的斜率；γw为水的容重（kN/m3）。

当为稳态渗流时， 单元体内流入和流出的流量在任何时间均相同，式（1）可变为下式：

2.2 有限元渗流方程

渗流控制方程采用加权余量的伽辽金方法求解，二维渗流方程的有限元格式可表示为：

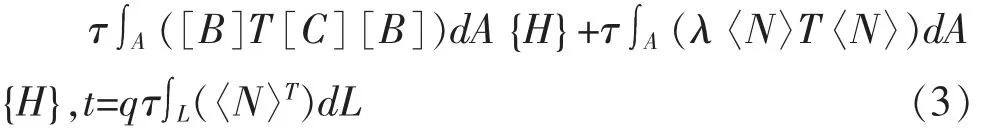
式中 ［B］为梯度矩阵；［C］为单元渗透系数矩阵；{H}为节点水头向量；〈N〉为插值函数向量；q为穿过单元边界的单位流量（m3/s）；τ为单元厚度（m）；λ为存储项， 对瞬态渗流等于mwγw；A为在单位面积上的求和符号；L为在单元边界长度上的求和符号。

有限元渗流方程可简化为下式：

式中 ［K］为单元特征矩阵；［M］为单元质量矩阵；{Q}为单元上施加的流量矢量。

当为稳态渗流时，水头不是时间的函数，式（4）可变为下式：

2.3 边界条件

当为稳态渗流时， 渗流控制方程的定解条件仅含边界条件，常见的边界条件有两类：

第一类边界条件： 当渗流区域的某一部分边界（比如S1）上的水头已知，法向流速未知时，其边界条件可以表述为：

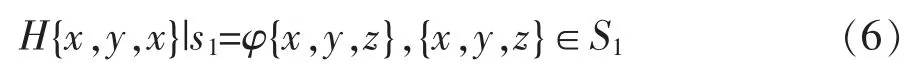
第二类边界条件： 当渗流区域的某一部分边界（比如S2）上的水头未知，法向流速已知时，其边界条件可以表述为：

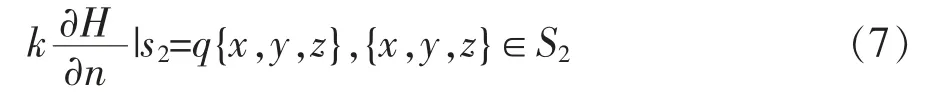
式中 s2为具有给定流量的边界段；n为s2的外法线方向。

3 算例

3.1 计算模型

计算模型如图1， 均质土坝坝高30m， 坝顶宽度8m，上下游坝坡坡比为1∶2.5，坝基覆盖层厚度20m，基岩深度为10m。 上游水位58m，下游水位32m。

图1 土石坝计算模型

3.2 计算参数

考虑均质土坝填筑材料受分层碾压施工方法的影响，坝体填筑材料按正交各向异性材料考虑，本次计算考虑了8种渗透系数比值（即竖向渗透系数ky与水平向渗透系数kx的比值（ky/kx）），其他材料为各向同性材料，渗透系数取值如表1。注：（1）ky/kx比值为1时， 坝体为各向同性；（2）ky/kx比值大表明竖向渗透性强，ky/kx比值小表明水平向渗透性强。

表1 材料渗透系数

3.3 计算结果及分析

计算结果主要分析坝体浸润线、 下游坝坡出逸点高程、单宽流量和最大渗透比降的变化规律。

3.3.1 浸润线

均质土坝浸润线如图2。 结果表明：随着坝体填筑材料竖向渗透系数ky与水平向渗透系数kx的比值逐渐减小，即水平向渗透性逐渐增强，坝体浸润线总体逐渐上升；当渗透系数比值ky/kx由20∶1降至10∶1时，坝体浸润线大致呈竖直线；当渗透系数比值ky/kx由1∶1降至1∶30时，坝体浸润线呈上凸型曲线，且位置不断升高；当渗透系数比值ky/kx为1∶10，1∶20，1∶30时，坝体浸润线位置较为接近。

图2 浸润线对比

3.3.2 出逸点高程

均质土坝下游坝坡浸润线出逸点高程变化曲线如图3。 结果表明：随着水平向渗透性逐渐增强，坝坡下游出逸点高程总体变化趋势为：平稳下降→缓慢上升；当渗透系数比值ky/kx由20∶1降低到1∶2时， 出逸点高程范围为31.9～32.8m，高差为0.9m，变化幅度约为坝高的3%；当比值ky/kx由1∶2降低到1∶30时，出逸点高程范围为31.9～36m，高差增至3.1m，变化幅度约为坝高的10.3%。

图3 下游坝坡出逸点高程变化曲线

3.3.3 单宽流量

均质土坝单宽流量变化曲线如图4。 结果表明：随着水平向渗透性逐渐增强，单宽流量变化趋势为：缓慢上升→快速上升；当渗透系数比值ky/kx由20∶1降低到1∶4时，单宽流量由0.6m3/d增加至6.2m3/d；当渗透系数比值ky/kx由1∶4降低到1∶30时， 单宽流量由6.2m3/d骤升至25.8m3/d，可见水平向渗透性增强对大坝渗流量有很大影响。

图4 单宽流量变化曲线

3.3.4 坝体渗透比降

均质土坝最大渗透比降变化曲线如图5。结果表明：当渗透系数比值ky/kx由20∶1降低到1∶2时，坝体最大渗透比降由0.311升至0.313， 变化基本趋于稳定；当渗透系数比值ky/kx由1∶2降低到1∶30时，坝体最大渗透比降由0.313快速降至0.301，表明渗透系数比值ky/kx对坝体最大渗透比降影响很小。

图5 坝体渗透比降变化曲线

4 结语

随着均质土坝填筑材料水平向渗透性能逐渐增强， 坝体浸润线呈上凸型曲线， 且位置逐渐上升； 坝坡下游出逸点高程和大坝渗流量均有较大幅度上升；而坝体最大渗透比降仅有微小上升，影响甚小。