基于粒子群可拓的南太平洋长鳍金枪鱼产量预测方法研究

袁红春，胡光亮，陈冠奇，张天蛟

(上海海洋大学信息学院 上海 201306)

长鳍金枪鱼(Thunnusalalunga)是南太平洋延绳钓的主要目标鱼种之一。准确的渔情预测可以指导渔民和渔业企业合理分配有限的捕捞努力量，减少寻找渔场的时间，从而大幅度降低渔业捕捞作业成本。近年来，大量学者对金枪鱼的资源密度与影响因子的关系进行了深入的研究[1- 6]。如Zagaglia等[5]使用广义加性模型(GAM)和广义线性模型(GLM)对长鳍金枪鱼渔场进行回归预测；宋利明等[6]使用支持向量机对不同水层的环境因子进行分析，得到了库克群岛海域长鳍金枪鱼栖息环境综合指数。虽然渔业作业数据及海洋环境数据的数据量庞大，但由于其复杂性和多变性，可进行数据分析和预测的样本量少，目前学者们多采用多元回归分析法[5]对渔场进行预测。回归分析法要求变量具有独立性和符合正态分布，但动态的海洋环境因子大都不符合正态分布，影响因子之间也不具有独立性。

以南太平洋长鳍金枪鱼为例，并结合多种影响因子，提出一种基于粒子群可拓神经网络的渔情预测模型，以丰富预测方法、提高预测水平。

1 材料与方法

1.1 数据来源

根据南太平洋长鳍金枪鱼的作业范围，选取135°W～110°E，5°S～40°S为研究海域。采用2000—2015年的数据进行研究，其中渔业作业数据来源于中西太平洋渔业委员会(WCPFC)的南太平洋延绳钓数据。海洋环境因子数据来源于美国国家海洋和大气管理局(NOAA)和欧洲哥白尼海洋环境监测服务中心(CMEMS)。

1.2 可拓神经网络模型

蔡文教授于1983年首先提出一门原创性学科—可拓学[7]。随着其理论框架的逐渐成熟与完善,对可拓神经网络[8- 10](Extension Neural Network，ENN)的研究也逐渐兴起，它是结合神经网络和可拓学的一种新的神经网络模型。

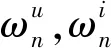
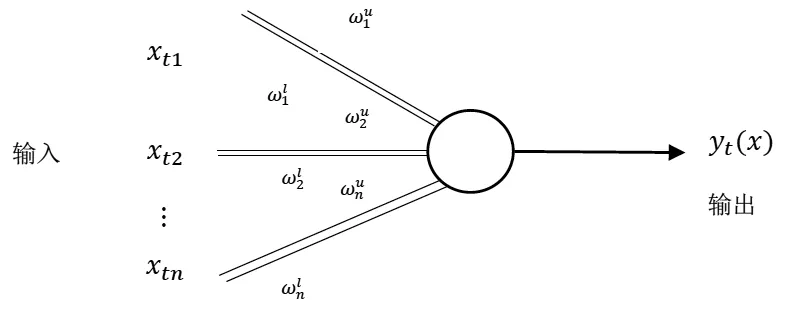
图1 可拓神经元结构Fig.1 Extension neuron structure

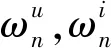
图2 ENN网络结构图Fig.2 ENN architecture

可拓学中的关联函数[13]作为ENN的激活函数，每一个输出神经元还包含一个求和函数和传递函数。其具体学习训练步骤如下：

1)分别建立样本物元模型，经典域物元模型和节域物元模型[11- 12]。

2)读入第t个样本Nc和其对应的期望输出类别。

3)建立关联函数并计算关联度。可拓神经网络的关联函数如式(1)：

Kij(xtj)=

(1)

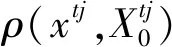
4)计算综合关联度。如公式(2)，Ki(xt)表示第t个输入样本与第i个输出类别的综合关联度。通过加权求和得到综合关联度：

(2)

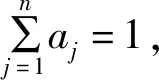
5)根据关联函数的性质，要求输入样本与输出类别的综合关联度值非负，即Ki(xt)≫0，本文采用函数作为输出神经元的传递函数，其公式如(3)。

(3)

取Si(xt)=max{Si(xt)}，如果i*=P，表明该样本通过ENN判别与其期望输出相符合，正确识别个数R+1，否则R不变。继续读入下一个训练样本，转到步骤2)。所有训练样本学习训练结束为一个学习过程。

6)一个学习过程结束后计算适应度函数，为下一步利用粒子群算法进行权值优化做准备。本文提出的适应度函数形式如公式(4)。

(4)

式中：T为样本总数；R为ENN预测正确的样本个数；Si(xt)=max{Si(xt)}。

1.3 粒子群优化

粒子群算法[15- 17](Particle Swarm Optimization，PSO)是一种基于群集智能的随机搜索算法。受到鸟群活动的启发，粒子群算法利用个体之间的交互，从而使群体在共享信息指导下在解空间中寻找出最优解。

PSO算法首先在解空间中初始化为一群随机粒子，每个粒子根据共享的群体信息动态地更新自己的速度和位置。算法每一次迭代中，粒子通过追踪两个“极值”对速度和位置进行调整，分别是个体寻找出的局部最优解pi和群体寻找出的全局最优解pg，粒子更新速度和位置如公式(5)、(6)：

(5)

(6)

(7)

式中：Tm为最大迭代次数；t为当前迭代次数；ωmax和ωmin为算法开始和结束时的权重。

粒子群算法训练时，每个粒子对应一组经典域参数，粒子的参数维度与一组经典域中的特征属性个数相对应，每个特征属性都有两个参数(上界和下界)，包含每种输出类别下的所有特征属性的经典域。其训练步骤如下：

1)初始化群体规模、参数维度、惯性权重、最大迭代次数和结束条件。初始化每个粒子的位置参数和速度参数，设定各个特征属性的节域和权重。

2)将粒子的位置转化为一组经典域，并带入到可拓神经网络模型中，对所有样本数据进行学习训练。一个学习过程结束后，根据公式(4)对每个粒子进行适应度值计算。

3)计算每个粒子的当前适应度，根据该粒子的历史最优适应度，更新个体历史最优粒子位置。

4)计算所有粒子的当前适应度，根据群体历史最优适应度，更新群体历史最优粒子位置。

5)检查是否满足算法结束条件，如不满足转到步骤6)，否则停止学习。获取当前群体历史最优位置为本次学习训练的最优解，即优化后的经典域。

6)更新惯性权重，根据公式(5)和(6)更新每个粒子的速度参数和位置参数。更新后的粒子转步骤2)继续训练。

1.4 层次分析法确定权重

不同的空间因子和环境因子对长鳍金枪鱼资源密度的影响程度不同，以每个影响因子的权重描述其对资源密度的影响程度。采用层次分析法(AHP)[18- 19]确定各因子的权重系数。该方法可使复杂关系之间的决策思想层次化，把决策过程中的定量和定性的因素结合起来，通过建立判断矩阵，排序计算和一致性检验后得到结果，避免了人的主观性导致特征属性权重与实际情况相矛盾的情况发生，提高了有效性。本文中选取的空间因子和环境因子共5个，分别为纬度、经度、海表温度、海面高度和叶绿素a质量浓度[20]，其权重确定步骤如下：

(1)构造比较矩阵：

(8)

(2)构造判断矩阵：

(9)

矩阵C=(cij)n×n为一致性判断矩阵，其中cb为一常数，在实际应用中常取cb=9；R=rmax-rmin称为极差；rmax=max(r1,r2,...,rn);rmin=min(r1,r2,...,rn)。

(3)计算权重并归一化：

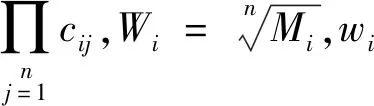
(10)

(4)进行一致性检验：

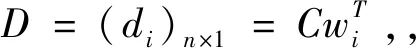
(11)

2 试验与结果

2.1 数据预处理

由于渔业作业数据和海洋环境因子数据空间分辨率不一致，需要经过数据匹配，统一转换为5°×5°区域的值。渔业作业数据和环境因子作业数据需经过数据净化，清除数据缺失的数据记录。单位捕捞努力量渔获量(CPUE)的大小常被作为资源丰度的相对指数来反映资源丰度的变化，其定义为：

(12)

式中：CPUE(i,j)为整经纬度(i,j)处的渔获率；Nfish(i,j)为该经纬度上的渔获尾数；Nhook(i,j)为该处的下构枚数。

研究中常使用三分位数将渔区按照CPUE的大小划分成若干个类别，从而将CPUE有效离散化[21]，适用于分类模型。由于渔业作业中各月产量差异较大，仅以历史CPUE的三分位点进行等级划分，不能有效地表示各月渔场的实际丰度水平，甚至会导致某些月份不存在高产区或者高产区较少，不利于指导渔业作业。因此借鉴文献[22]中的分类方法，将渔区以各月CPUE的三分位数分位点66.7%和33.3%划分为高产区、中产区和低产区三类。

本文选取即时性较强、获取方便的环境遥感数据，包括海表温度(sst)、海面高度(ssh)、叶绿素a质量浓度(Chl- a)，结合空间因子纬度(latitude)和经度(longitude)作为影响因子。不同的影响因子，量值单位以及变化范围差别较大，为防止小数值量被大数据量所淹没，对数据进行归一化处理。本文采用的归一化公式如下：

(13)

式中：y为归一化后的值；x为实际值；xmin为对应特征取值范围的最小值；xmax为其最大值。处理后的数据如见表1，其中2000—2014年共8787条数据为训练样本，2015年743条数据为测试样本。

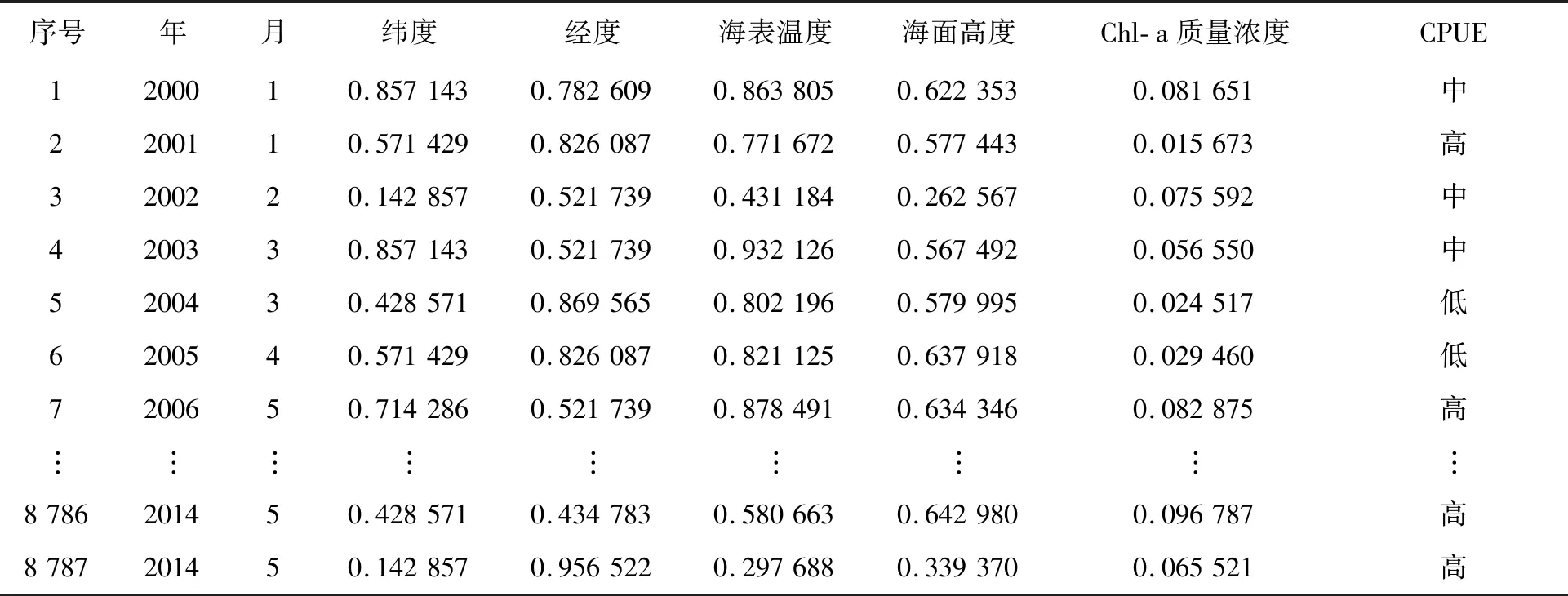
表1 部分试验数据Tab.1 Partial experimental data

本文使用召回率(Recall)作为评估标准[23]，其计算方式如下：

(14)

式中：Pi表示i类产量等级的预测召回率；tpi为预测正确的该产量等级的记录条数；fpi为其预测错误的记录条数。

2.2 试验过程

试验流程见图3。可拓神经网络中的权值优化训练，即为对3个产量等级的经典域进行优化。其中每个产量等级有5种特征属性，共有15个量值区间，30个参数(每个量值区间有上界和下界两个参数，即15个参数对)，即每个粒子有15个位置参数对和15个速度参数对。

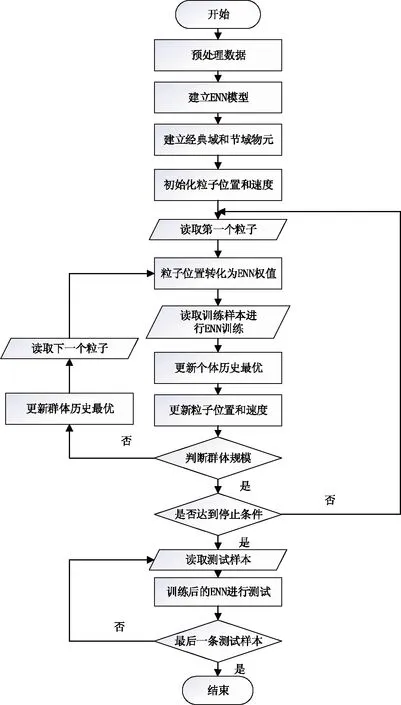
图3 试验流程Fig.3 Experimental process

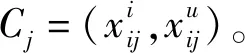
(15)

(16)

(17)

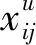
各特征属性的权值比重通过上文层次分析法获得，纬度、经纬、海表温度、海面高度、叶绿素a质量浓度(Chl- a)等权值比重分别为0.45、0.26、0.15、0.09、0.05。群体规模Nm=200，最大迭代次数Tm=500，算法开始时惯性权重ωmax=0.9，结束时惯性权重ωmin=0.4，学习因子c1=c2=2,经过多次训练，得到一组较为满意的经典域，如表2所示。

表2 PSO优化确定的经典域

2.3 试验结果

使用优化后的ENN对表1中的测试样本进行测试(表3)。优化后的ENN模型总召回率达到68%，表3同时给出了使用朴素贝叶斯分类模型、BP神经网络模型构建南太平洋长鳍金枪鱼预测模型的对比试验结果。其中朴素贝叶斯分类模型采用文献[24]的基于FastICA方法独立成分分析的朴素贝叶斯方法，BP神经网络采用5-512-3结构。

表3 不同模型的试验结果对比Tab.3 Experimental result comparison of different models

3 讨论

3.1 不同产区的预测结果

由表3可以看出，与其他两种预测模型相比，粒子群可拓神经网络模型总体召回率[23]最高，在高产区有较大的优势。在实际渔业捕捞作业中，作业位置一般对高产区的预测结果更依赖。但中产区的预测效果明显低于高产区和低产区，可能由于只按照月CPUE的三分位点进行长鳍金枪鱼的产量等级划分[22]，导致预测方法中的产量等级划分界限不清晰。而实际捕捞作业中受天气、政策等因素影响，渔场的实际CPUE值可能高于或低于试验中的产量等级标签。

3.2 与其他模型的比较

国内外进行了大量渔情预测模型研究，但多采用统计学模型，如对比试验中的朴素贝叶斯方法，用类似于数据库查询的方式进行预测[25]，通过对历史数据的频率统计得到先验概率和条件概率,从而计算出后验概率。该方法要求各个环境变量之间相互独立，模型进行训练前要对各变量进行独立成分分析，不仅增加了模型的复杂性，还造成数据信息量的损失。近年来，也出现了人工神经网络[26- 27]在渔情预测方面的应用。神经网络的学习训练过程即为网络连接权值的确定过程，但结构复杂的网络训练非常耗时，如对比试验中的BP神经网络方法，采用5-512-3结构。本研究中的可拓神经网络采用5-3结构，没有隐含层，结构简单。在学习速度上，粒子群可拓神经网络模型采用惯性权重线性递减的策略[17]，算法前期学习速度大，以适应网络在全局范围内大步长训练学习，后期学习速度小，适应网络在小范围内进行小步长训练学习，比BP网络采取的变速学习速度设计较为合理。

3.3 其他影响因素

利用粒子群算法优化权值，可解决可拓神经网络中经典域不易确定的问题，减少主观因素的影响。但是长鳍金枪鱼的渔场分布及洄游移动，除受到试验中的5种关键因子影响外，还可能受到时间因素、海水流速、海面风场、溶氧质量浓度、海水盐度等因素的影响[28]。因此，在下一步的研究工作中需要收集更多的环境参数数据，并将渔场的时间序列因素[29]加入到模型中进行更多影响因子的综合分析，以期更准确地为渔民和渔业企业提供作业基础资料 。

4 结论

使用粒子群优化可拓神经网络的方法，构建了南太平洋长鳍金枪鱼预测模型，与传统方法相比准确率有所提升，同时为渔情预测提供了一种新的思路。在今后的研究中需要收集更多的海洋环境因子数据，并结合时间序列因素加入到训练中，进一步提高预测准确率。