某铝合金钢圈螺栓孔的疲劳寿命特征
孙鹏峰
某铝合金钢圈螺栓孔的疲劳寿命特征
孙鹏峰
(厦门日上集团股份有限公司,福建 厦门 361000)
铝合金钢圈作为当前轮毂设计中主流产品,其疲劳度的实验对于产品的性能检测非常重要。螺栓孔作为钢圈应力的集中区,其疲劳开裂可以用力预测钢圈的疲劳寿命。采用弯曲疲劳实验方法,对钢圈螺栓孔进行有限元分析,进而用史密斯公式预测疲劳寿命。通过分析,可以为优化钢圈设计和分析预测钢圈寿命提供借鉴。
钢圈;螺栓孔;疲劳寿命;应力分析
汽车行驶过程中会受到多重的应力作用,钢圈作为力矩传导的关键部件,其受力特征十分复杂,钢圈承受的力根据路况的不同而随机施加到轮毅上。从载荷类型来看,主要有弯曲载荷和交变扭转载荷,因此极易造成钢圈疲劳失效。根据受力特征分析,钢圈所受载荷会在螺栓孔周围形成应力集中,是导致疲劳开裂的主要诱因。因此,借助有限元分析对钢圈螺栓孔进行复杂的受力分析,然后采用疲劳度建模分析钢圈螺栓孔的疲劳程度,以此指导未来产品进行优化设计。
1 铝合金钢圈疲劳实验方法选择
1.1 径向疲劳实验
径向疲劳试验是针对钢圈的径向受力进行的分析,径向作用力主要来自轮胎胎压和外部挤压力,会对钢圈的疲劳强度产生影响。因此径向疲劳度实验需要给轮胎施加1.2~1.7倍的正常胎压,然后在实验台上通过转鼓施加给钢圈径向的力γ,不断增加径向载荷,直到钢圈螺栓孔出现疲劳裂纹。径向载荷公式如下所示:
(Z)=Z·=γ·(1)
式(1)中:(Z)为垂直于钢圈半径的力矩;Z为方向的垂直力;为安装平面间的偏距。
径向实验要求在没有达到实验目的的基础上,钢圈具有承载不小于50万次的等量受力能力。但是,通过大量的实验发现,在径向受力实验中,钢圈的焊接总是先于螺栓孔开裂,因此,该实验无法稳定地检测到钢圈螺栓孔的疲劳强度。
1.2 弯曲疲劳实验
弯曲疲劳实验是考察钢圈承受扭矩作用力下的疲劳强度,钢圈所承受的扭矩主要来源于螺栓的拧紧力矩和弯矩。在弯曲实验中不需要考虑胎压对钢圈的作用,因此实验中只需要施加螺栓拧紧力矩即可。
实验过程中需要施加弯矩,弯矩通过液压缸和加载轴进行加载。弯矩大小由以下公式计算得出:

式(2)中:为加载轴的长度。
弯曲实验要求在钢圈极限承受能力下至少可以承载 30 000次的同等载荷。该实验可以对螺栓的拧紧力矩以及来自侧向的弯矩进行考察,通过大量的实验数据分析可知,在该实验中钢圈首先在螺栓孔处开裂,其他部位极少会出现裂纹。因此,可以认为螺栓孔的疲劳度对于弯矩比较敏感,因此该实验方法可以用于分析钢圈螺栓孔的疲劳寿命。
1.3 双轴疲劳实验
径向疲劳实验和弯曲疲劳实验是在双轴疲劳实验的基础上进行的两个轴向的受力简化模型。简化后的模型不能充分考虑两个轴向作用力的交互,因此分析的疲劳度精确性还有待提升。另外,两个实验采用不同的实验设备,不能在同一个钢圈上进行实验,得出的实验结论也略有差异,还增加了实验的成本。德国弗劳恩霍夫在此基础上提出的全新双轴疲劳实验方法,可以有效避免以上弊端。采用的实验设备可以同时施加垂直和侧向力,实验条件更加接近实际工况。但是该实验设备比较昂贵,且实验周期较长,因此,没有得到大规模应用。鉴于此,本文采用弯曲疲劳实验分析钢圈螺栓孔的疲劳寿命。
2 铝合金钢圈螺栓孔应力特征及寿命分析
2.1 载荷计算
钢圈的设计中充分考虑了钢圈的受力强度、重量以及行驶过程中的热传导情况,因此采用A35G高性能铝合金材料设计而成。铝合金材料保证了钢圈对于受力强度的要求,同时还可以满足轻量化的设计初衷。同时,钢圈上预留了10个通风孔可以有效地进行钢圈散热,通风孔与螺栓孔内外交叉排列,中心夹角为18°。
根据公式(2),可以计算出弯矩:
=(+)s×=24 873.5 N·m
实验设备的加载轴长为0.679 m,因此可以得到轴末端载荷为:
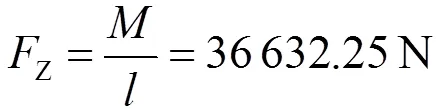
该实验中的受力分析是基于钢圈的静态分析模型。实验中钢圈处于静止状态,外力通过旋转弯曲力矩的形式施加给钢圈。基于以上计算数据可以对螺栓孔的应力和疲劳度进行进一步的分析。
2.2 螺栓孔应力分析
实际运行工况下钢圈是通过螺栓与刹车盘连接的,螺栓通过拧紧力将两个贴合面按压在一起。由于螺母和螺栓的受力情况比较复杂,因此,需要进行模型的简化,在两个贴合面上设置应变化分析其受力情况。实验结果如图1所示。

图1 螺栓拧紧力对轮副的作用
根据钢圈的受力分析以及大量的实验数据可知,螺栓孔附近是应力的集中区,因此,对于螺栓孔的应力分析,可以在螺栓孔周围选取不同的观测点,进行应力的提取。
选取应力集中区的可能最大的应力受力点进行取样,施加25 kN·m>=24.873 525 kN·m的弯矩。然后建立模型,取轮辐表面为~平面,螺栓孔垂直方向为轴。
通过图1可知,在上述实验条件下,从8个不同的方向施加周期性的载荷,螺栓孔受到的应力主要来自于Mises应力和轴应力,其轴和轴应力较小,且二者趋于一致;另外,轮辐应力的最大方向为第一载荷方向,因此,在螺栓孔的疲劳度实验中要以该方向的应力作为极限承受点。
2.3 疲劳寿命预测
钢圈在实际工况下,决定其寿命的往往是来自于局部的应变力集中点,该点的疲劳度即为整个钢圈的疲劳度。因此在钢圈的疲劳度寿命分析中采用局部应力应变法,通过史密斯公式进行其寿命的计算。2个采样点在最大应力方向的疲劳度寿命如表1所示。
表1 疲劳寿命计算结果
序号采样点1采样点2 Mises应力4.36E+054.78E+05 X轴应力2.15E+062.68E+06 Y轴应力9.45E+091.03E+07 Z轴应力2.14E+075.02E+07
从表1可以看出,在四个方向应力的寿命疲劳度分析中,其寿命的疲劳度从小到大依次为:Mises应力、轴应力、(轴应力/轴应力)。
由此可见,影响钢圈螺栓孔疲劳度寿命的主要因素是Mises应力,其次是轴应力。轴应力和轴应力对于钢圈螺栓孔的疲劳度寿命影响最小。另外,从两个采样点的疲劳度寿命来看,不同方向的疲劳度寿命相差不大,因此,也可以反映出该实验钢圈实际的合理性。
3 疲劳实验结果分析
通过上述分析可知,考察钢圈的螺栓孔疲劳度寿命,中国普遍采用弯曲疲劳实验。通过计算钢圈所能承受的最大弯矩为24 873.5 N·m,因此实验弯矩取25 kN,当周期性施加载荷时,在401 833次螺栓孔处发生开裂现象。可以认为该钢圈螺栓孔的疲劳寿命为401 833次。中国国标中对于钢圈的使用寿命规定为,最大载荷下极限承受次数不低于 30 000次。由此可以说明,该钢圈满足中国国标要求。
由于弯曲疲劳试验忽略了不同方向应力的交互作用,因此对于疲劳度的预测由于实际情况会略有差异。通过实测值与理论值的分析发现,其相对误差为8.5%。因此,弯曲疲劳实验作为钢圈螺栓孔疲劳寿命的预测方法具有一定的可行性。
4 总结
综上所述,螺栓孔作为钢圈的应力集中部分,其寿命与钢圈的寿命直接相关。因此,螺栓孔的疲劳度寿命分析对于钢圈的失效分析具有实用价值。通过实验发现,螺栓孔在弯矩作用下,其受到的应力主要来自于Mises应力和轴应力。采用史密斯公式预测的寿命值与实测值误差不大,由此可见,在钢圈的疲劳度实验中可以采用弯曲疲劳实验方法和史密斯公式进行其寿命的分析。
[1]尹显波,李健,张南媚,等.某铝合金钢圈螺栓孔的疲劳寿命研究[J].山东工业技术,2017(24):273.
[2]郑战光,王佳祥,杨兴,等.对汽车钢圈疲劳试验寿命的模糊预测[J].机械设计与制造,2017(10):85-87,91.
[3]余泉.汽车钢圈的疲劳强度分析与形状优化[D].柳州:广西科技大学,2015.
[4]李冰,耿雪霄,黄位健.汽车钢圈疲劳寿命的有限元分析[J].机械设计与制造,2011(7):125-127.
[5]王波,管迪华.汽车钢圈多轴疲劳寿命预计[J].汽车工程,2002(2):119-121,129.
U463.34
A
10.15913/j.cnki.kjycx.2019.24.028
2095-6835(2019)24-0069-02
孙鹏峰(1981—),男,福建宁化人,本科,中级工程师,主要研究方向为机械工程。
〔编辑:严丽琴〕

