学生推理能力培养浅析
杨静
[摘要]小学阶段是学生各项能力形成的基础时期。小学阶段形成的推理意识和能力,极大地影响着学生今后的学习过程。教师要重视对学生推理能力的培养,让学生能够尽早形成相对严谨的推理思路,以作为数学学习的支撑,并将这一能力迁移到其他学科。
[关键词]小学数学;推理能力;培养
[中图分类号]G623.5 [文献标识码]A [文章编号] 1007—9068(2019)32—0074—02
课程标准提出要注重对小学生核心素养的培养,而推理能力是小学数学核心素养培养的重要部分。在小学数学中,推理通常指的是逻辑推理,可以分为归纳推理和演绎推理两种。这两种能力对小学生在数学方面的学习,以及形成真正的数学能力来说,有着至关重要的作用。从学习的心理来看,推理通常是指由一个或几个概念(前提)推出新判断(结论)的过程,这个过程不仅体现在数学学习中,在日常生活中也很常见。
一、培养推理能力的必要性
推理的过程具有严密的逻辑关系,因此推理相较于其他数学能力来说,有着更为强大的力量。在实际生活中,推理也是最有力的论证说理手段,很多职业都需要一定推理能力的辅佐,很多场合也都是由推理发挥着最主要的作用。小学阶段是学生推理能力形成的基础时期,小学阶段所形成的推理基础,会极大影响学生今后的学习和生活,这也是课程标准要求注重学生小学阶段推理能力培养的原因。让学生尽早形成较为严密的推理思路,一方面是使之可以更快地适应最需要推理能力支撑的数学这门学科,另一方面是能够引导他们将推理能力迁移到其他学科,以获得更全面的发展。
二、培养推理能力的操作性
1.挖掘教材,渗透推理
客观事实表明,无论是何种能力的形成都需要依附在一个具体的知识点来学习。换言之,离开了具体的学习素材,学生是无法真正获得这项能力的。对于小学阶段的学生来说更是如此,他们的思维能力尚处在一个较弱的水平,必须挖掘教材,将素材具体化,他们才能够更好地思考。
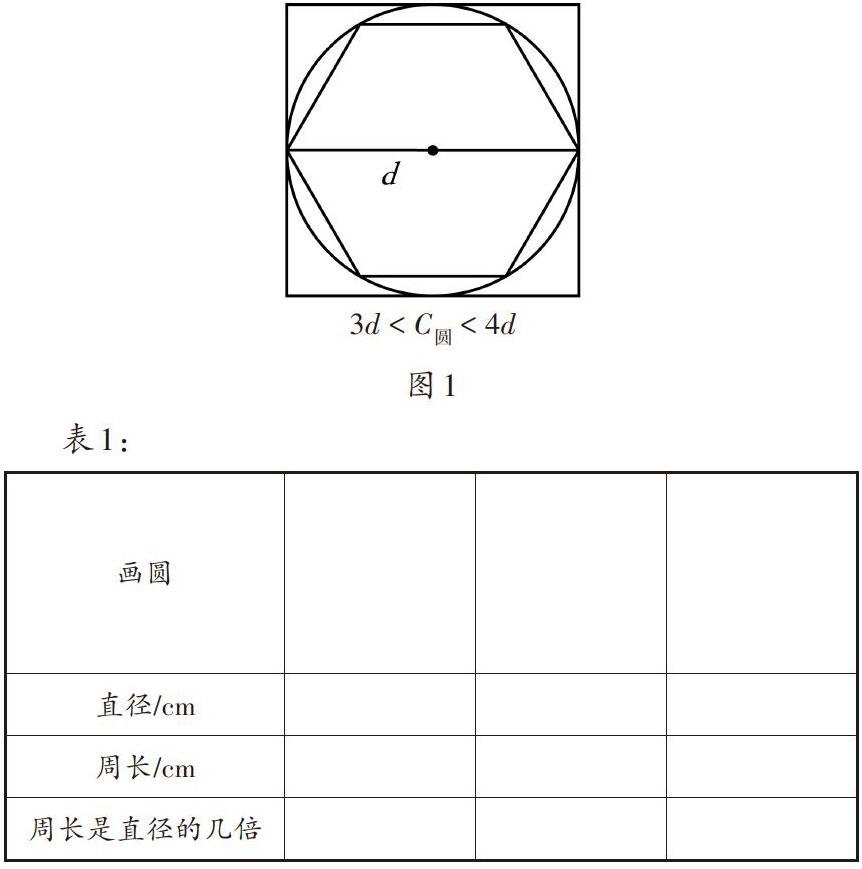
例如,教学“圆周率”时,教材用两个例题来帮助学生探究圆的周长与直径的关系,推导过程分为两步。第一步,先估算圆的周长。在正方形内画一个最大的圆,则圆的直径与正方形的边长相等,由于这个圆的周长比正方形的周长短,推算出圆的周长比直径的4倍小一些。接着,在圆内画一个最大的正六边形,则正六边形的边长与圆的半径相等,由于圆的周长比正六边形大一些,推算出圆的周长比半径的6倍(即直径的3倍)大一些(如图1)。此时,学生对于圆周长与直径的关系已经有了初步的感知。第二步,根据归纳推理得出圆的周长到底是直径的几倍。采用的是不完全归纳法,要求学生先用圆规画三个大小不同的圆,然后用细绳和直尺量出每个圆的直径与周长,将数据记录在表格中,并计算出圆的周长是直径的几倍(如表1)。学生通过对比分析三组数据,发现其中的规律:圆的周长都是直径的3倍多一些。最后,教师引出圆周率的概念。
以上推导过程看似简单,学生实际操作起来却花了不少时间,但事后学生在涉及圆周率相关的问题时,错误率很低,表明这样的教学方式是值得的。在教师的引导下,学生通过自主实践探究,对数据进行归纳总结,不仅加强了对知识点的理解和记忆,还有效培养了推理能力。
2.抓住瞬间,善用推理
分析教学实际情况不难发现,小学阶段数学学科的难点主要在解应用题,学生在应用题环节需要大量运用演绎推理这一方法,推理过程中又常常会擦出不一样的火花。教师需要在学生对初步学习一个知识点之后,依靠自己的教学经验及教学智慧抓住可以培养学生演绎推理能力的瞬间,帮助学生有效利用所学知识解决实际数学问题,乃至生活中遇到的问题,从而增强学生的推理能力。
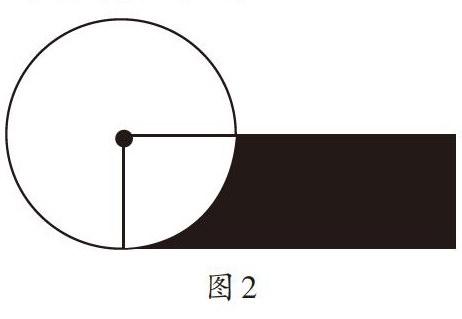
例如,教学“计算涂色部分的面积”时,有这样一道题:如图2所示,已知圆的半径是4厘米,长方形的长是12.56厘米,求涂色部分的面积。
大部分学生会先求出长方形的面积和圆面积的1/4,再将两部分相减,即得出涂色部分的面积。这时,有一位学生指出:“这个长方形的面积和圆的面积是相等的。”这是一个精彩的教学瞬间,在其他同学还比较疑惑时,教师应该抓住这个瞬间继续追问:“为什么呢?”引导这位学生说出推理过程:“在学习圆的面积时,我们知道把一个圆沿着半径平均分成若干等份,再重新拼成一个近似的长方形,这个长方形的面积等于圆的面积,宽是圆的半径,长是圆周长的一半。这道题虽然没有明说,但从图中也能看出长方形的宽是圆的半径,再根据题意可以算出长方形的长是圆周长的一半,从而推出长方形的面积就等于圆的面积。因此,求涂色部分的面积就是求圆面积的3/4。”如此精彩的推理过程,引来全班同学的热烈掌声,大家豁然开朗。
由于这样的推理建立在圆面积公式的推导方法以及用转化法解决问题的策略等旧知的基础上,学生很容易就可以分析出图形间的关系,并推理出更加简便的计算涂色部分面积方法。学生像这样通过自我演绎推理出知识点,比教师直接教授获得的满足感更强烈,同时有效强化了推理能力。
3.养成习惯,主动推理
推理能力的形成和习惯的养成一样,如仍需要在教师提醒下实施则并不算是真正形成了推理能力,关键在于学生的主观能动性。学生在遇到新问题之后,自发地运用自己掌握的知识和已有的推理能力去尝试解决,这才算是真正形成了推理能力。简单地说,就是包括推理能力在内,许多能力形成的最终标志是学生在遇到问题时能够主动运用自身的能力去解决。
小学数学的教学中,教师经常强调要学生牢固掌握基础知识,做到运用自如。要达到运用自如的水平,离不开一定程度的训练,但是需要注意的是这里的训练与“题海战术”是不同的概念。推理能力的训练要求学生通过反复训练掌握基础知识,再将这些知识内化,进而能够熟练灵活地运用。
例如,教学“加法运算定律”时,就有很多可以用多种运算律进行计算的题目,运用不同的定律,计算的难易程度也有很大差别。学生在将基础知识完全内化之后,就能在脑海中形成一种数学意识。比如,连加肯定是用加法交换律或者加法结合律,连乘是用乘法交换律或乘法结合律,既有加法又有乘法可以用乘法分配律,等等。
遇到问题会熟练运用最为迅速简便的解决方法,这些都需要学生在做题中自己发现题目特点,并进行归纳整理。当然,要形成这样的能力不是一朝一夕就可以达成的,还需要教师耐心引导,让学生在潜移默化中增强自身的推理能力,并主动运用到学习和生活中。
三、培养推理能力的长期性
在实际教学中,我们很容易发现,学生的推理能力并不是能够轻而易举形成的。由于应试的压力,在课堂教学中,教师不得不将重心倾向于基础知识点的巩固上,而学生的推理能力往往是在缺乏目标性的指导下自然形成的,这就导致学生推理能力的培养和课堂基础知识的教学很难融合。因此,要培养学生的推理能力,不仅需要教师自身的努力,还可能要付出应试成绩不理想的代价。此外,对于教师来说,在师范教育中缺乏对能力培养这块的训练,这就导致一些教师缺乏对学生能力培养的意识,在实际教学时很容易出现心有余而力不足的情况。由此看来,在小学数学教学中培养学生的推理能力任重而道远,具有长期性。
总而言之,推理是數学的基本思维方式,是数学发现的重要手段,也是帮助学生理解数学抽象性的有效工具。在教学中,教师应把推理能力的培养贯穿于学生学习的整个过程中,有意识地培养学生的能力,让学生学会主动运用,最终形成习惯。但是,学生推理能力的培养并不是一蹴而就的,需要付出许多时间与精力,教师和学生都需要长期坚持,确实任重道远。

