混凝土重力坝功能叠合区坝体应力计算方法探析

周天鸿，秦根泉，曾一夫，葛淑敏

（1.河海大学 港口海岸与近海工程学院，江苏 南京 210098；2.四创科技有限公司，福建 福州 350100；3.江西省水利规划设计研究院，江西 南昌 330029）

1 研究背景

混凝土重力坝是水利枢纽工程中一种重要的挡水建筑物。随着水利工程建设的高速发展，我国在建的混凝土重力坝的结构体型也越来越复杂且形式多样。例如，因挡水坝高度不同，出现了不同程度的坝体与坝后建筑物的功能叠合区，因叠合区结构重叠程度的不同，对坝体应力的影响以及应受到的重视程度也不同。

鉴于重力坝功能叠合区这一特殊结构在水利枢纽工程中的复杂性以及其越来越常见，目前很多学者对重力坝坝体与坝后建筑联合受力做了研究。武颖利［1］采用有限元法研究了某水电站在不同载荷工况下，坝体及厂房的应力及位移，对厂房坝段的设计提出了一些改进。吴海林等［2］采用有限元法分析了某坝后式水电站在不同厂坝连接型式下坝体和厂房的应力，得出了采用平缝灌浆或整体连接的形式，有利于改善受力条件的结论。周秋景等［3］针对三维有初始间隙的接触问题，采用有限元混合法研究了观音岩水电站混凝土坝和坝后式厂房的相互作用，得出了分缝大小对坝体、厂房应力和应变的影响规律。兰文改等［4］采用有限元法对某混凝土重力坝厂房坝段在两种工况下的应力应变进行复核，得出了一些有益的结论。杜丽惠等［5］采用考虑接触的三维有限元方法，对某水电站典型坝段的厂房和大坝的应力变形及它们通过联接缝的相互作用情况进行了数值模拟，研究了联接缝对厂房应力和稳定性的影响。牛志国等［6］结合某水电站的工程实际，用有限元法研究了不同厂坝连接方式对坝体和厂房的抗滑稳定、应力及变形的影响。熊斌伟［7］分别用材料力学法与有限元法对坝体以及厂房结构做了计算对比分析。陆宗磐［8］对万家寨水利枢纽工程的厂坝连接设计进行了研究。Liu等［9］基于偶应力理论对重力坝厂坝结构做了分析，得出了坝体应力集中区域的应力以及位移分布规律结论。

在以往的研究中，多对坝身与坝后结构采取分离分析或联合分析，未对不同计算方法对于此类复杂结构应力分析上的适用性进行讨论。混凝土重力坝功能叠合区结构复杂，由于计算资源和分析手段限制，采用有限元法对结构进行大规模的全面模拟比较困难，在一些情况下也是没有必要的，而材料力学法在一些情况下得出的计算结果偏保守，可能会影响对工程应力安全判定的准确性，所以在对混凝土重力坝功能叠合区进行应力分析时，如何合理的选择计算方法与计算模型是非常重要的。本文主要对某水利枢纽工程的安装间坝段混凝土重力坝功能叠合区的坝体应力计算模型与计算方法进行研究，对比分析在对该类复杂结构的工程情况下不同分析计算方法的计算结果，分析不同计算模型和计算方法对计算结果及安全评价结论产生的影响，指出存在功能叠合区的重力坝结构在进行坝体应力计算时可能会出现的问题，并提供解决思路。

2 工程实例

案例工程是一座以防洪为主，兼顾供水、发电等的综合利用水利工程，为大（2）型Ⅱ等工程。工程采用混凝土重力（闸）坝及河床式厂房组合式布置方案，主要建筑物沿坝轴线从左至右依次为：左岸碾压混凝土非溢流坝、表孔溢流坝、低孔溢流坝、发电厂房和右岸碾压混凝土非溢流坝等。本文研究对象为右岸非溢流坝安装间坝段，安装间布置在发电厂房主机间右侧，位于右岸非溢流坝下游侧，因该坝段相邻的发电厂房坝段机组安装定位的要求，安装间结构镶嵌在右岸非溢流坝上，对坝体局部断面有所削弱，形成了一定程度的功能叠合区。

安装间坝段上游部分为挡水坝，坝顶高程65.50 m，坝顶上游设2.10 m宽牛腿，坝顶宽度8.0 m，上游坡上部采用垂直坡面，下部采用1∶0.2的斜坡面，斜坡面高度10 m；下游坡59.63 m高程以上垂直，59.63 m高程以下坡度1∶0.75。坝体内设有灌浆排水廊道，断面尺寸2.5 m×3.5 m（宽×高）。安装间上游侧最大挡水混凝土厚度为14.05 m，安装间与挡水坝体为整体结构，装卸层高程为46.90 m，向下设二层，第一层布有空压机室和风机室，高程为42.35 m，第二层为透平油库，高程为37.35 m，为板梁柱框架结构，下游侧墙厚度为1.70 m。安装间坝段下游为发电厂区，回填高程46.70 m。安装间坝段上游挡水部分和基础底板为碾压混凝土，厂房建筑部分采用常态混凝土。

3 材料力学法计算及成果分析

材料力学法是重力坝设计规范中坝体应力计算的一种常规方法，该法计算简便，适用性强，其基本假定是：坝体水平截面上的垂直正应力呈直线分布。计算时将重力坝挡水坝坝体按照悬臂式结构进行简化，对功能叠合区坝段，不能考虑结构整体受力，属偏保守简化，计算上下游面边缘应力公式如下［10-11］：

计算部位选取安装间底板高程36.85 m处挡水坝坝体上下游面，该处为悬臂梁水头差最大部位，是大坝安全分析的关键部位。计算中不考虑挡水坝下游侧安装间板梁柱框架结构对坝体的支撑作用，主要荷载为：（1）坝体自重；（2）上、下游静水压力；（3）计算基底面扬压力。计算工况以及工况水位见表1，混凝土弹性模量24 GPa，泊松比0.167，容重2400 kg/m3，水容重1000 kg/m2。

考虑坝体内部渗水时，坝体内部的渗流水面线采用假定的稳定渗流状态的水面线，渗流水面线以下混凝土容重取浮容重。实际当中，因发生高水位工况的历时较短，稳定渗流可能尚未形成，因此计算假定的渗流水面线偏高，混凝土实际浮容重区域比假定的小，故使用该假定渗流水面线假定时的计算结果偏保守。各工况的坝体渗流水面线见图1。

经计算5种工况上游面安装间底板高程▽36.85 m处竖向应力结果见表1。由表1可知，使用材料力学法计算该坝段坝体应力，在3种上游面高水位工况下上游面安装间底板▽36.85 m处均出现拉应力，其中防洪高水位工况时拉应力值最大，为0.13 MPa。根据重力坝安全判定标准，重力坝在所有工况中上游面均不应出现拉应力［12］，考虑到重力坝功能叠合区的特殊性，能否以该计算结果作为判定大坝安全性的依据需进一步分析。

因为材料力学法以保守方法对计算结构进行了简化，上游挡水工况下，没有考虑安装间板梁柱结构对重力坝坝体的支撑作用，本文工程安装间结构嵌入坝体深度达17.3 m，在最底部因功能叠合坝体断面削弱的部分占坝底面的宽度近1/2，对坝体断面的侵占情况较为严重。这种结构会使得结构受力情况、应力大小以及分布状况发生较大的改变，为使得计算结果更符合实际，对大坝坝体的安全性做更准确的判定，需要进一步的细化计算模型，使用有限元法进行复核计算。

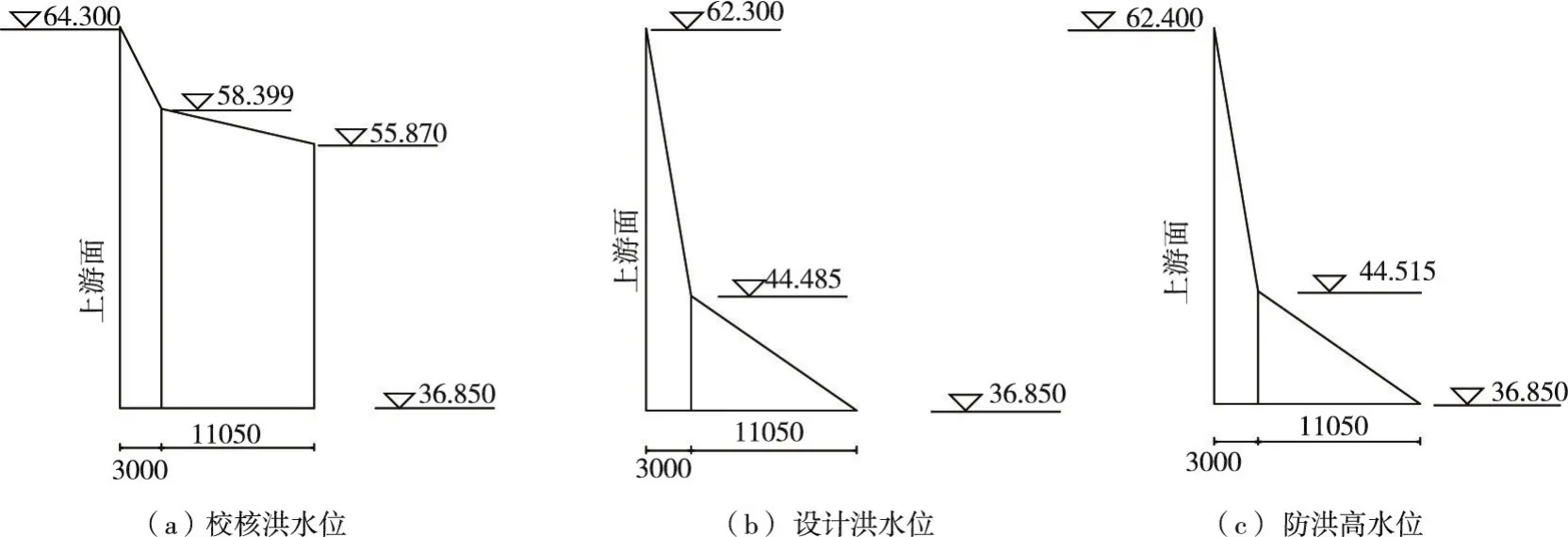
图1 各工况坝体渗流水面线

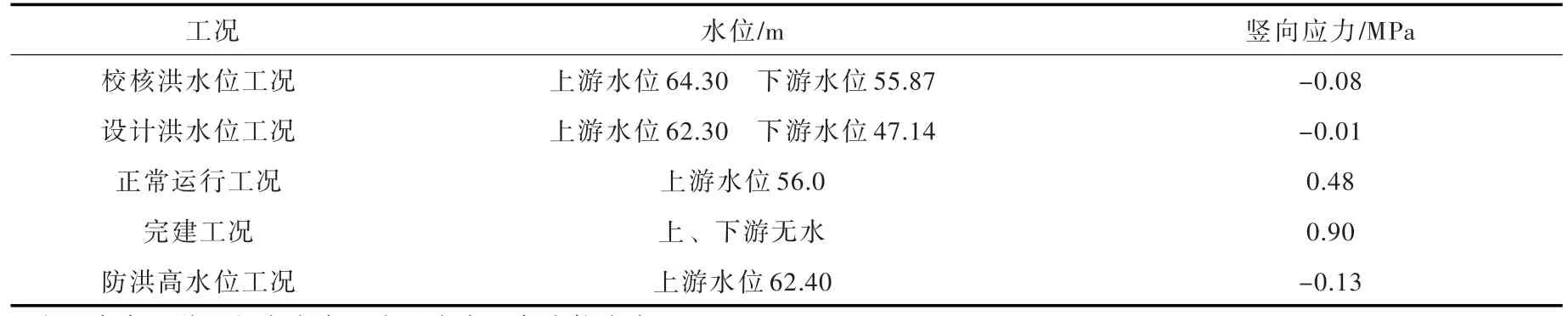
表1 安装间底板高程36.85 m处上游面竖向应力计算成果

4 有限元法计算及计算成果分析

4.1 有限元模型建立图2、图3为本文计算的三维有限元网格模型，以左右岸方向为X轴，向右岸为正；以上下游方向为Y轴，向下游方向为正；竖直方向为Z轴，竖直向上为正。计算区域上，坝前、坝后取1.5倍坝高，深度方向自坝底向下60 m高。研究表明，计算边界约束条件情况对计算结果有较大影响，为了更好的模拟边界约束条件，计算边界条件为：基础底部、前后侧及左右侧均为法向约束，其余为自由边界，坝体和安装间左右两侧法向约束。计算模型中考虑了安装间的板梁柱以及坝体混凝土分区、基岩等部位。坝体、安装间、板梁柱结构等均采用8节点6面体等参单元，基础中部分单元采用6节点退化棱柱体单元，共有单元213 254个，结点229 656个。

4.2 有限元计算成果及分析本文采用SAPTIS有限元分析软件进行计算，SAPTIS有限元分析程序擅长混凝土坝温度控制分析、非线性安全分析以及钢筋混凝土联合作用分析等，由中国水利水电科学研究院结构材料研究所采用FORTRAN语言编制，使用时间近20年。SAPTIS程序包括多种单元库（四面体单元、标准六面体单元等）、多种求解方式（直接求解、迭代方式求解）和各种本构模型，具有单元库丰富、求解速度快、效率高等优点，程序完全按照软件工程的要求进行编制和测试，结果准确可靠。

有限元计算法工况水位及荷载情况与材料力学法相同，由于使用材料力学法时在防洪高水位工况、校核洪水位工况以及设计洪水位工况上游面均出现了拉应力，有限元法对材料力学法计算时出现拉应力的3种工况进行坝体应力复核分析。

图3 坝体和安装间模型

为研究坝体上游面、坝体内部以及安装间结构的应力，从模型中提取典型断面进行应力分析。由于有限元计算模型考虑了坝后安装间板梁柱结构对挡水坝体的支撑作用，3种计算工况下坝体上游面及内部均为压应力，未出现拉应力，最大压应力出现在坝踵，为2.2 MPa（防洪高水位工况），坝体应力分布规律为随着高程升高，压应力逐渐减小。同时，计算应力等值线图中显示在梁板柱结合处有一定的拉应力存在，最大拉应力值为0.56 MPa（设计洪水位工况）。该部位为钢筋混凝土框架柱结构，对拉应力有承载能力，经复核，计算结果中该部位的拉应力值不足以对结构形成破坏［15］。

从3种工况的计算结果分析，坝体应力的大小及不均匀性和上游水位值变化趋势基本对应，但校核洪水位工况下，大坝校核洪水标准为2000年一遇，而下游厂房的校核洪水标准为200年一遇，此时下游厂房已经进水，下游水位产生的静水压力对挡水坝上游静水压力有一定的抵消作用。因此，坝体应力及不均匀性最大值出现在防洪高水位工况，即大坝下游厂房达到进水临界高程时对应上游水位工况。防洪高水位工况上游面以及大坝典型剖面竖向应力等值线图见图4，图中正为拉应力，负为压应力。

从各工况计算结果可知，经建立考虑安装间结构联合受力的有限元模型，使用有限元法复核计算坝体应力，在3种水位组合工况下，上游挡水坝体均处于受压状态，未出现拉应力，符合坝体应力安全性评价标准要求。

4.3 不考虑安装间板梁柱结构计算模型坝体应力计算及计算结果对比为与材料力学法计算结果进行充分比较，尝试在有限元法计算模型中不考虑安装间板梁柱结构支撑作用，分析工况为防洪高水位工况。计算得出的上游面竖向应力图以及坝体结构剖面竖向应力等值线图见图5，图中正为拉应力，负为压应力。

由计算结果可知，采用该计算模型的有限元法计算结果显示，虽然大坝上游面大部分处于受压状态，但在安装间底板高程附近（36～38 m）仍出现了约0.1MPa的拉应力，与材料力学法的计算结果较为相近。

4.4 不同计算模型及计算方法结果对比分析取有限元法两种计算参数在防洪高水位工况下在安装间底板高程处典型点的应力计算结果和材料力学法计算的安装间底板高程处应力计算结果进行对比，见表2。

有限元法与材料力学法在不考虑安装间结构受力情况下的计算结果在上游面安装间底板高程处均出现了约0.1 MPa大小的拉应力，均不符合坝体应力安全性评价标准要求，而在使用有限元法在考虑安装间结构受力情况下的计算结果显示，上游挡水坝体上游面均处于受压状态，未出现拉应力，符合坝体应力安全性评价标准要求。经过对比3组计算结果可知，在该研究对象中，对于大坝坝体在使用材料力学法与有限元法两种计算方法进行坝体应力安全性评价时出现了相反的结果，但坝体应力分析在同一种计算参数下采用不同的计算方法，得出的计算结果对大坝的安全评价结论是基本一致的。材料力学法在对功能叠合区坝段进行应力计算时，无法考虑安装间框架结构对坝体的支撑作用，得出的计算结果偏保守，可能会影响对大坝应力安全性的评价；有限元法可建立更细化的计算模型，在计算中能够考虑安装间框架结对坝体的支撑作用，通过优化计算模型来对计算结果的准确性进行修正，计算结果更为贴合实际，能对大坝的应力安全性进行更为准确的评价。

图4 考虑安装间结构受力计算模型防洪高水位工况下竖向应力等值线图（单位：MPa）

图5 不考虑安装间结构受力计算模型防洪高水位工况竖向应力等值线图（单位：MPa）

表2 防洪高水位下不同计算方法与计算模型安装间底板高程处竖向应力

5 结论

研究对象中采用材料力学法进行坝体应力计算时，未考虑安装间框架结构的作用，属于偏保守简化，计算结果显示防洪高水位工况时上游面安装间底板高程处出现了0.132 MPa的拉应力，但由于其偏保守简化导致计算结果偏保守而不够精确；采用有限元分析方法计算坝体应力时，建立模型中考虑了安装间框架结构的作用，得出了所有工况坝体均处于受压状态的更为贴合实际的计算结果。

考虑重力坝与安装间板梁柱结构联合受力时有限元计算结果显示：防洪高水位、校核洪水位以及设计洪水位3种工况下大坝上游面竖向应力均为压应力，坝踵部位最大竖向压应力出现在防洪高水位工况，约2.2 MPa；大坝典型剖面仅在安装间板梁柱结合处等结构突变处出现了拉应力，最大值出现在设计洪水位，约为0.56 MPa，坝体应力分布规律基本符合常规规律。

在不考虑安装间板梁柱结构联合受力的情况下，采用有限元分析方法计算，在上游防洪高水位工况，大坝上游面安装间底板高程附近出现了0.105 MPa的拉应力，与材料力学法计算结果相近，说明有限元法与材料力学法在采用相同的计算参数进行应力计算时，得出的计算结果是相近的。

有限元分析方法相比材料力学法能够考虑复杂的结构体系，在计算中通过优化计算模型来得出更为贴合实际的计算结果，是一种对重力坝功能叠合区这一特殊的复杂结构应力分析的有效方法，计算结果可作为评价重力坝功能叠合区坝体应力安全性的可靠依据。

本文在考虑坝体渗流水面线时未考虑洪水过程，以假定产生稳定渗流确定水面线，并简化为的直线形式，简化得出的计算水面线比实际水面线高，该假定对计算结果的影响是偏保守的。