水泵水轮机导叶间不同周向偏距对水力效率的影响研究

贺 蕾，高忠信

（中国水利水电科学研究院，北京 100038）

1 研究背景

我国对可逆式水泵水轮机的研究始于20世纪70年代初。很多专家学者针对混流式水泵水轮机过渡过程［1］、水泵水轮机参数选择及优化［2］、“s”特性［3］、驼峰特性［4］、水力性能三维数值模拟以及各个水力部件进行了研究［5］。

活动导叶对于可逆式水泵水轮机水力性能至关重要，一直是水力机械研究领域的研究热点，王乐勤等［6］研究了活动导叶开度对水泵水轮机泵工况的影响，为水泵水轮机的操作工况选择提供依据，也可以指导水泵水轮机的优化设计；邵卫云等［7］学者对导叶不同步装置（MGV）降低蜗壳进口压力的机理进行了研究，发现MGV装置在一定程度上降低了蜗壳进口压力的最大值；李小芹等［8］学者对抽水蓄能电站中球阀协同导叶关闭的水力瞬变过程控制方式进行研究，研究表明合理地选择导叶与球阀的控制规律，即可显著改善水泵水轮机装置水轮机工况甩负荷过渡过程的动态品质，降低抽水蓄能电站引水系统的水压上升值；李琪飞等［9］学者针对水泵水轮机导叶开启瞬态过程进行了数值分析，得到速度、压强随时间的瞬态变化规律，探讨水泵水轮机导叶开启过程的流场特性；Nennemann等［10］学者，针对水泵水轮机活动导叶振动问题，运用三维CFD数值模拟方法进行了研究，提出了解决方案。杨波等［11］学者采用混合紊流模型计算了组合叶栅内部流场，选取适当重合度与栅距比，叶栅性能得到大幅提高；徐伟等［12］学者通过数值模拟研究了串列叶栅的流动特性及机理；宋文杰等［13］学者利用数值模拟方法研究了串列叶栅前后排叶片相对位置变化对立新性能的影响以及作用机理。

水泵水轮机中固定导叶和活动导叶组成串列叶栅，固定导叶与活动导叶周向偏距即两组叶栅周向相对位置对于水泵水轮机的水力性能有一定影响，目前，关于活动导叶周向偏距对于水力性能影响的相关研究较少。本文运用三维定常数值模拟的方法，对水泵水轮机活动导叶不同周向偏距情况下的内部流动进行模拟计算，并对不同周向偏距水力效率影响进行比较研究。

2 混流式水泵水轮机模型

图1为混流式水泵水轮机模型示意图。该水泵水轮机模型中固定导叶20枚（包含鼻端固定导叶1枚）、活动导叶20枚、转轮叶片7个。表1为混流式水泵水轮机各过流部件参数。其中，D1为叶轮进口直径，D2为活动导叶分布圆直径。

运用数值模拟的方法，在不同周向偏距下，对以下4种工况进行计算：设计工况下的水轮机和水泵、水轮机小开度工况、水轮机大开度工况。图2为混流式水泵水轮机导叶区示意图，其中，b为固定导叶和活动导叶尾部夹角；a为相邻的固定导叶尾部之间夹角。

图1 混流式水泵水轮机模型示意

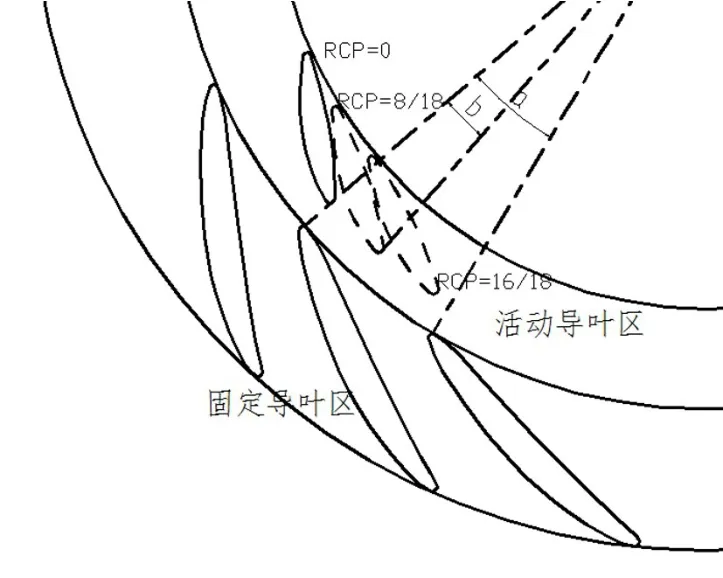
图2 混流式水泵水轮机导叶区示意

表1 混流式水泵水轮机参数

定义固定导叶与活动导叶周向偏距RCP=a/b［11］，前排固定导叶周向位置固定不变，改变后排活动导叶周向相对位置，能得到RCP的值分别为0、2/18、4/18、6/18、8/18、10/18、12/18、14/18、16/18、1，从而就得到了10种不同固定导叶和活动导叶组合方式。当RCP=1时活动导叶位置和RCP=0时活动导叶位置重合，即RCP=0-1为一个周期，RCP再增加就进入下一个周期。所以这里取RCP=0～16/18，9种固定导叶和活动导叶组合方式。图2所示，分别为0、8/18、16/18，3种组合示意图，随着RCP值的增大，活动导叶区周向沿着逆时针移动。

3 数值计算方法

数值模拟求解所用的商业软件是CFD的CFX，控制方程如下：

质量守恒方程（连续性方程）：

动量守恒方程：

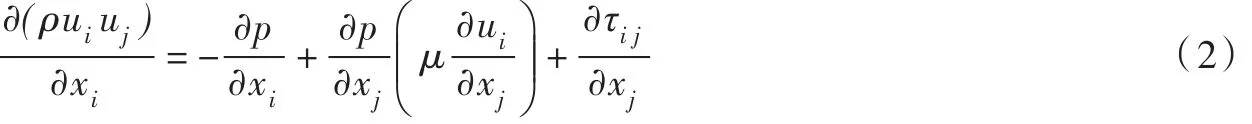
控制方程采用基于有限元的有限体积法进行离散，近壁面采用自动避免处理函数，湍流模型采用SSTk-ω模型控制方程如下：

其中，Gk为湍流动能项，Gω为耗散方程项，Γk和Γω代表k和ω湍流动能的有效扩散系数，Yk和Yk代表k和ω的发散项，Dω是正交发散项。Sk和Sω用户自定义。

边界条件设置如下，导叶和转轮区、转轮和尾水管的动静交界面采用混合面法；固体壁面给无滑移边界条件；进口给定的边界条件为总压；出口给定的边界条件为静压。

模型计算域划分以及计算网格划分如图3所示，并附有导叶区及转轮局部放大图。计算域包括蜗壳、固定导叶和活动导叶、转轮、尾水管四个计算域。网格划分采用ICEM网格划分软件，蜗壳采用四面体非结构网格，固定导叶和活动导叶、转轮、尾水管采用六面体结构网格。

图3 混流式水泵水轮机模型的网格图

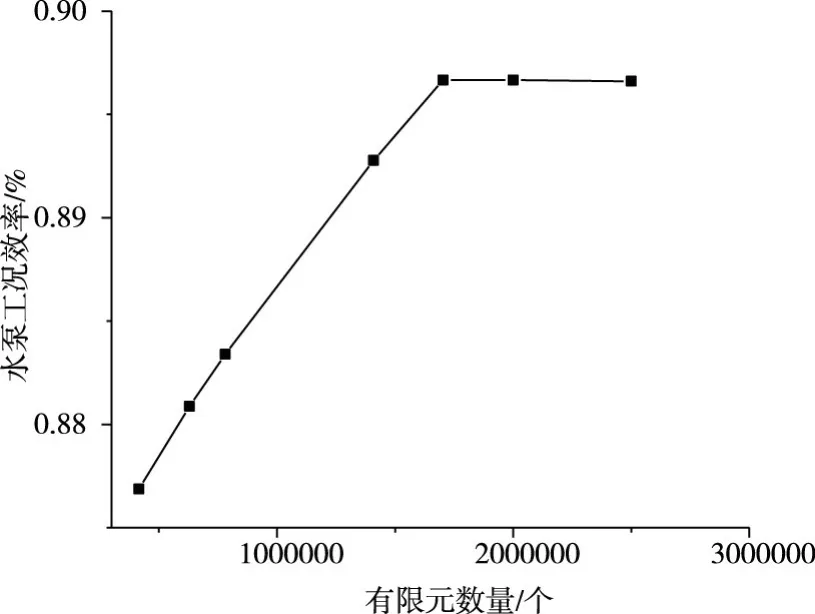
图4 有限元数量和机组效率曲线

为了明确网格数对计算结果的影响，在水泵工况下做不同网格数量的离散，再分别进行计算，网格数量从50万逐渐增加到300万。图4为模型不同网格数目对应水泵工况下效率变化曲线图，可以看出当网格数量大于150万的时，计算结果逐渐稳定在一个定值。本文采用计算域总网格数量为158万个。

4 计算结果及分析

4.1 计算工况水轮机设计工况、水轮机大开度工况、水轮机小开度工况、水泵工况4种计算工况下，活动导叶开度及水头如表2，机组转速n=1200 r/min，进口边界条件，给定模型进口水头或扬程，再根据水头或扬程计算得到进口总压。

4.2 RCP对水力效率的影响图5为水轮机设计工况、水轮机小开度工况、水轮机大开度工况、水泵工况，4种工况下周向偏距RCP与效率关系变化曲线图。

表2 水泵水轮机4种计算工况参数

从图5可知，随着周向偏距RCP的增大，在水轮机设计工况下水力效率先减小后增大，在RCP=0达到最大值，RCP=12/18～4/18为高效率区；水轮机大开度工况下水力效率先减小后增大，在RCP=12/18达到最大值，RCP=0～12/18为高效率区；水轮机小开度工况下水力效率先增大后减小，在RCP=12/18达到最大值，RCP=12/18～4/18为高效率区；在水泵工况下，水力效率先增大后减小，在RCP=4/18达到最大值，RCP=0～8/12为高效率区。

综上，考虑机组设计工况和非设计工况下机组性能，周向偏距RCP在0～4/18之间比较合理。

图5 RCP与效率关系变化曲线

4.3 水轮机工况下机组内部流场分析水轮机设计工况下RCP=0～1与机组效率曲线如图6所示。随着周向偏距RCP增大，效率整体呈先下降后增大变化规律，其中在RCP=12/18处出现波动；在RCP=0处机组效率达到最大，RCP=8/18处机组效率降到最低。取效率最高点RCP=0，机组效率最低点RCP=8/18进行分析。

对不同周向偏距RCP下水轮机工况下机组各个过流部件损失情况进行统计，其中导叶区损失最多，蜗壳区损失占比较小。定义水轮机工况下除转轮外各过流部件损失L1如下：

注：转轮区损失由机组总损失减去除转轮外各过流部件损失得到，P进口总压为各过流部件进口处总压，P出口总压为各过流部件出口总压，L1单位为%。

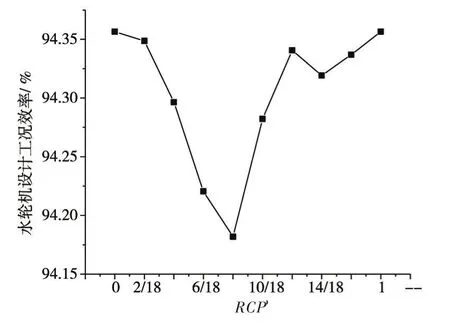
图6 水轮机设计工况RCP与机组效率曲线

图7 水轮机设计工况转轮与尾水管损失

表3为水轮机设计工况下不同周向偏距RCP对应的各过流部件损失情况。从表中可知，导叶区损失占比最多，转轮尾水管损失随RCP变化较大；蜗壳区损失占比最小，随RCP基本没有明显变化。图7为水轮机设计工况下转轮和尾水管总损失。从图中可知，随着周向偏距RCP的变化，转轮和尾水管损失变化规律与机组效率变化规律相反，机组效率越高，转轮尾水管部分损失越小。

取z=0截面与活动导叶出口面相交得到的圆弧上速度，得到活动导叶出口速度变化如图8。根据出口速度计算得速度方差，RCP=0和RCP=8/18方差分别为0.23298和0.45089，对应效率最低的RCP=8/18时，导叶出口速度波动大，效率最高RCP=0时，导叶出口速度波动较小。

图9为水轮机设计工况下导叶区与转轮区z=0截面压力云图，比较可以发现右图最低效率RCP=8/18时活动导叶出口处较左图最低效率RCP=0时出现了更大范围的低压区。图10为水轮机设计工况导叶区与转轮区z=0截面速度云图，比较可以发现右图最低效率RCP=8/18时活动导叶出口处速度比左图最高效率RCP=0时的速度出现更大的不均匀。

表3 水轮机设计工况各过流部件损失

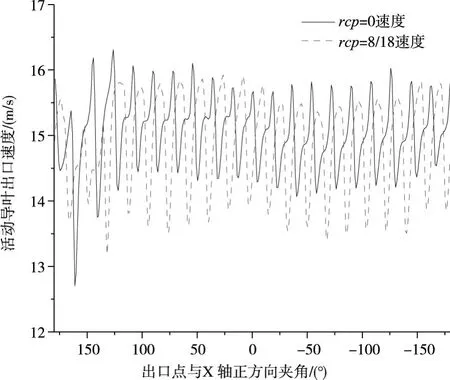
图8 活动导叶出口速度变化

水轮机设计工况下，周向偏距RCP的变化，会造成活动导叶出口处速度分布变化，速度分布不均匀性比较大时，导致转轮和尾水管内损失增大，效率降低。水轮机大开度、小开度工况下，随着周向偏距RCP的变化，效率增加或减小原因与水轮机设计工况相同。在这里不做详细分析。

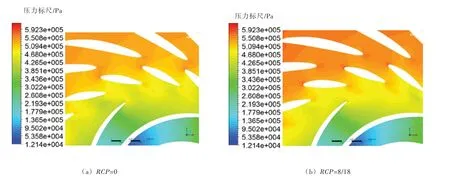
图9 水轮机设计工况导叶区与转轮区z=0截面压力云图

4.4 水泵工况下模型内部流场分析周向偏距RCP=0～1和水泵机组效率变化关系示意图如图11所示。水泵工况下，随着RCP的增大，效率先增大后减小，在周向偏距RCP=4/18时达到最大，周向偏距RCP=12/18时达到最小值。

图10 水轮机设计工况导叶区与转轮区z=0截面速度云图

对水泵工况下机组各个过流部件损失情况进行统计，其中导叶区损失最多，尾水管损失占比最小。定义水泵工况下除转轮外各过流部件损失L2如下：

注：转轮区损失由机组总损失减去除转轮外各过流部件损失得到，P进口总压为各过流部件进口处总压，P出口总压为各过流部件出口总压，Q为进口流量，，M为转轮的扭矩，L2单位为%。

表4为水泵工况下不同周向偏距RCP对应的各过流部件损失情况。从表中可知导叶区损失最多且波动最大；转轮和尾水管损失波动较小。图12为周向偏距RCP和水泵工况下导叶区损失关系图。

综上，随着RCP的增加效率先增大后减小，而机组导叶区的损失则先减小后增大。可以推测，在水泵工况下，周向偏距RCP的变化对机组导叶区内部流动产生了较大影响，进而使水泵工况下效率降低。

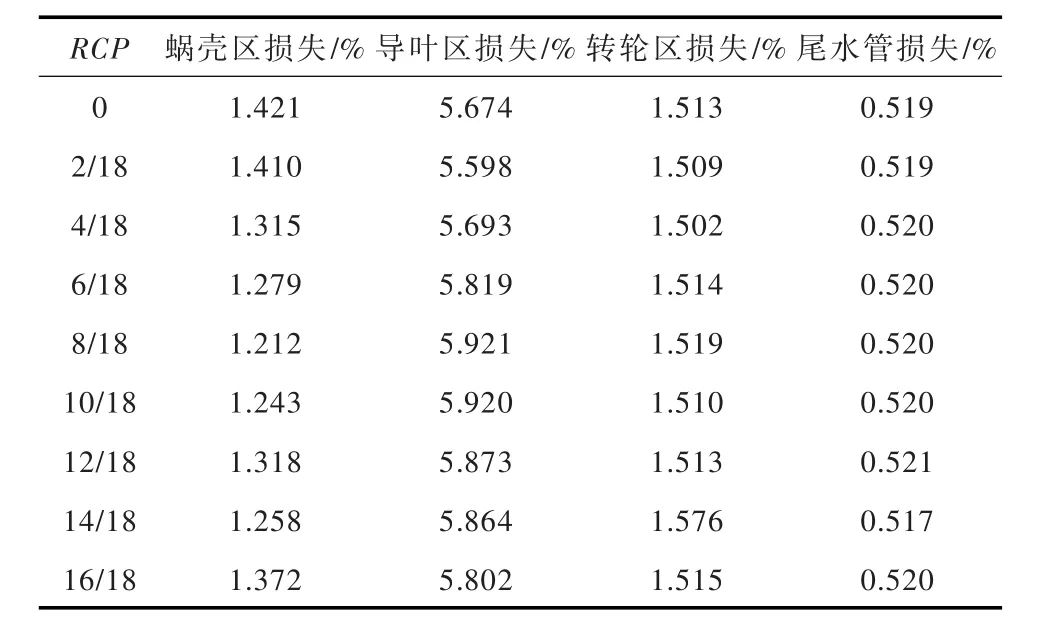
表4 水泵工况各过流部件损失

取z=0截面与活动导叶出口面相交得到的圆弧上速度，得到活动导叶出口速度变化图如图13。根据出口速度计算得速度方差，RCP=4/18和RCP=10/18方差分别为1.19983和1.37294，对应效率最低的RCP=10/18时，导叶出口速度波动大，效率最高RCP=4/18时，导叶出口速度波动较小。从图中可知，两种周向偏距下，从180°到-120°之间速度波动几乎相同；在-120°至-150°之间，周向偏距RCP=8/18时，活动导叶出口速度波动突然增大，查看模型得知该区域靠近固定导叶鼻端。

取水泵工况下高效率点RCP=4/18，低效率点RCP=10/18进行比较分析。

取水泵工况下z=0截面鼻端附近导叶区及蜗壳区速度云图如图14，左图为RCP=4/18高效率点，右图为RCP=10/18低效率点，由图可知，在水泵工况下机组效率较低时，周向偏距RCP的变化，造成靠近固定导叶鼻端的活动导叶区、固定导叶区以及蜗壳区流速不均匀，进而影响到水泵工况下水力效率。

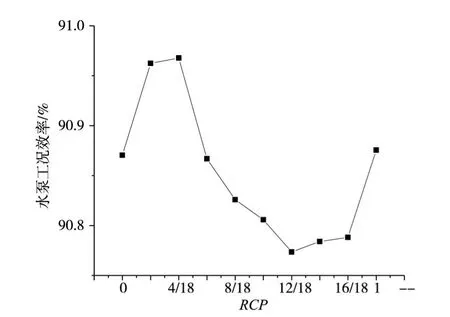
图11 水泵工况RCP与机组效率曲线

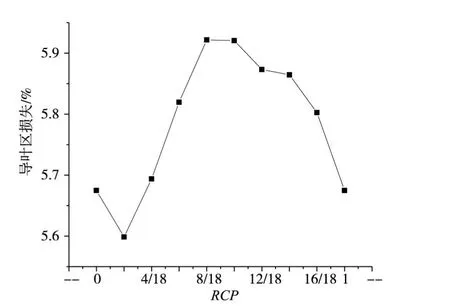
图12 水泵工况R C P与机组导叶区损失

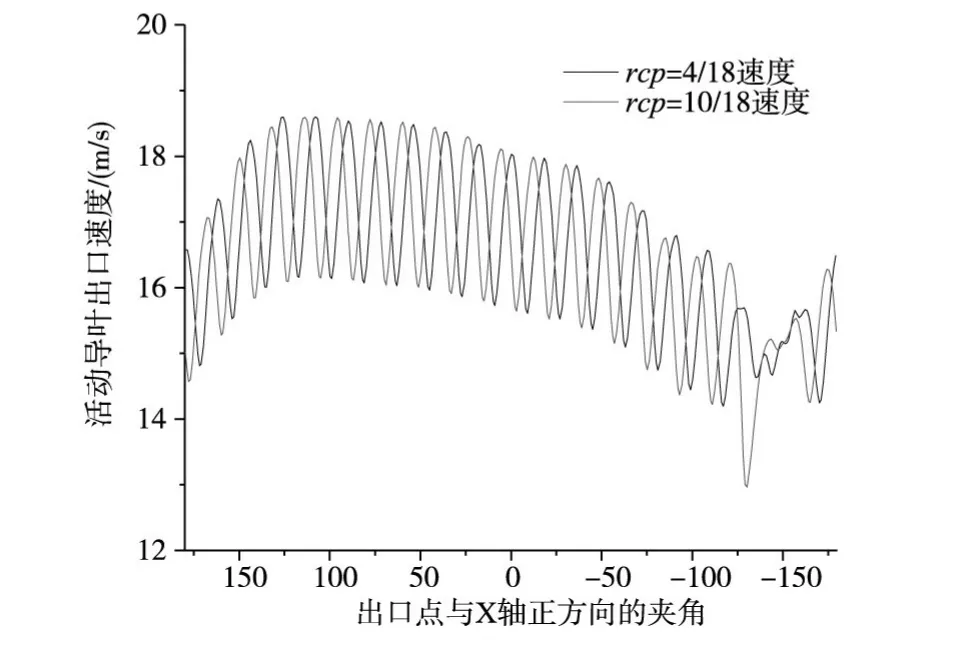
图13 水泵工况活动导叶出口速度变化

图14 水泵工况z=0截面鼻端附近导叶区速度云图

5 结论

（1）随着周向偏距RCP的增大，在水轮机模式下，设计工况和大导叶开度工况下水力效率先减小后增大，小开度工况下水力效率先增大后减小；在水泵工况下，机组效率先增大后减小。考虑机组设计工况和非设计工况下机组性能，周向偏距RCP在0～4/18之间比较合理。

（2）水轮机工况下，周向偏距RCP的变化引起水力效率降低因素为，造成活动导叶出口处速度分布不均匀，转轮和尾水管内损失增大，最终影响到效率；例如，RCP=0和RCP=8/18活动导叶出口速度方差分别为0.23298和0.45089；对应效率最低的RCP=8/18时，导叶出口速度波动大，转轮和尾水管损失为1.83%；效率最高RCP=0时，导叶出口速度波动较小，转轮和尾水管损失为1.688%。

（3）水泵工况下，周向偏距RCP的变化引起水力效率下降的因素为，造成靠近固定导叶鼻端的导叶区以及蜗壳区流速不均匀，进而导致效率降低。例如，RCP=4/18和RCP=10/18活动导叶出口速度方差分别为1.19983和1.37294；对应效率最低的RCP=10/18时，导叶出口速度波动大，导叶区损失为5.920%；效率最高RCP=4/18时，导叶出口速度波动较小，导叶区损失为5.693%。