点·链·网,复习课的价值构建
——人教版“多边形的面积复习”例谈
□ 张伟明
一、缘起
近期,笔者接到了上一节“多边形的面积复习”公开课的教学任务。这一课内容被编排在人教版教材五年级上册,是在学习了长方形、正方形、平行四边形、三角形和梯形面积后对面积体系进行的第一次系统的梳理,要求学生站在更高的平台上来俯视以前学习的零散的有关面积的知识点,将知识连点成线,连线成网。
笔者对本校15位教龄在5年以上的数学教师进行访谈后发现,近70%的教师通过大量收集习题、试卷,辅以“爆炒冷饭”式的知识点讲解,让学生在反复训练中达成复习目标;少部分教师采用“练习一校对一再练习一再校对”的教学方式,把学生会做每一道复习题作为唯一的教学目标。这样的复习课能被学生接受吗?复习课究竟该怎么上?
二、策略思考
在区教研员和同事们的帮助下,笔者执教了“多边形的面积复习”一课,形成了对复习课的一些思考。
(一)注重激活,在数学情境中重温“知识点”
激活学生脑海中的知识点是复习课展开的重要前提。教师应创设丰富的数学情境,让学生置身于问题解决的情境中,激发学生探索。教师适时捕捉有价值的生成,并以此为基础引导学生在交流和思考中提升对数学本质的认识,形成数学方法、意识和思想。
本课的导入环节,教师在出示了一组互相垂直的线段(如图1)后,提问:“这组线段让你想到了以前学过的什么平面图形?”在经过短暂的思考后,学生纷纷举手。起点不高但贴近学生认知的问题情境,点燃了学生的学习热情,学生搜寻着头脑中已有的知识点,进而关注平面图形的本质属性——互相垂直的底和高。教师则不失时机,让学生计算想象出来的图形的大小,于是很自然地就出现了10×4,10×4÷2两组算式,同时学生根据算式想象出了长方形、平行四边形和三角形等(如图2),揭开了多边形面积这一单元复习的序。教师通过唤醒学生原有的知识经验,自然而然地抛出了课题——多边形的面积复习。紧接着教师和学生带着“面积该怎么计算?面积公式又是怎么推导出来的?”这两个问题共同浏览电子课本,进一步回顾了三年级以来所有多边形面积的学习内容。这并不是一种简单意义上的再现,而是一种复习方法的指导。回顾是整理的前提,是复习的第一步。在这一步后,由点及链的复习就变得顺理成章。
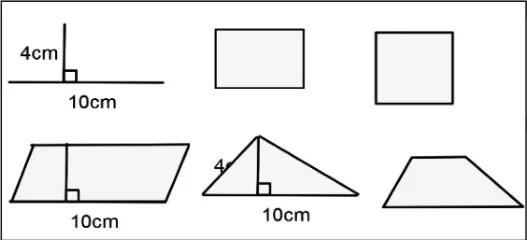
图2
(二)注重梳理,在自主探究中完善“知识链”
星星点点的知识,在问题解决情境中得到了激活。此刻,适时的梳理就显得尤为重要。知识点在梳理中连成知识链,复习从点状收拢成线状。在复习中,教师应留给学生思考的时间和空间,把复习梳理的主动权真正交给学生,让学生在动手实践与探究中自主把知识点链接起来,从而培养学生自主梳理的能力。
本课的梳理环节中,在学生回顾了教材,激活了原有的知识点,并在练习纸上记录下多边形面积的公式后,教师引导学生回忆图形面积公式的推导过程,感受面积公式在推导上存在的联系。教师在学生交流过程中辅以课件操作,真实再现平行四边形、三角形、梯形等多边形面积公式的推导过程(如图3),将学生置身于推导情境中,让推理有据可循。教师适时给予评价“是的,把平行四边形的面积转化成长方形的面积,这样就推导出了平行四边形面积公式,那跟它有关的长方形的面积公式是怎么来的你们知道吗?那同样是转化成平行四边形的还有……?”进一步帮助学生感受到这些表面上看起来独立的知识,其实它们之间存在着千丝万缕的关系。学生在自主探究回忆知识过程中充分应用分类、比较、转化等数学思想方法,加深了对知识的理解,链接的是知识的本质。至此,一个个零散的知识点因为内在的联系慢慢地串联为知识链。
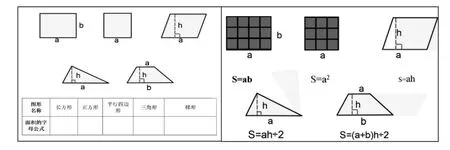
图3
(三)注重提升,在对比反思中构建“知识网”
零碎、分散的知识点,在学生自主梳理中得到了整合。但要将教材的知识进行内化与巩固,作进一步提升,还需要教师引导学生探寻知识间的联系,让学生在知识点的对比与对知识链的反思中,将发展变化中的数学知识链结成知识网,构建脉络清晰的知识模块,在不断完善学生认知结构的同时,让学生获得认识事物的普遍方法。
本课的提升环节中,在学生把知识点链接起来,从学习经验步入理性思考后,教师试图让学生在更广阔的空间里去比较、合作、反思。教师以“看来图形间是有联系的,这样的推导关系你能用线连一连吗”的设问,更有序地推进思考。教师先让学生独立思考,然后在组内议一议,再进行全班的汇报。在分析、比较各小组所获知识时,学生不难发现:除了正方形外,平行四边形可以转化成长方形,三角形、梯形可以转化成平行四边形。正是因为存在这样的转化关系,所以我们可以根据长方形面积计算公式推导出平行四边形面积计算公式。而这也正是图4中双向箭头所表示的含义。这样,学生记忆中那些孤立的、分散的、无序的、认识模糊的概念,通过再现、整理、归纳等方法,串成了线,连成了片,结成了网,纵横沟通,形成了条理化、系统化的知识网络。而在思维碰撞中,学生经历了由模糊到清晰、由疑惑到顿悟、由割裂到联系、由片面到全面、由理性到感性的认识过程。他们进一步发现,虽然长方形是面积公式推导的源头,但是平行四边形才是图形转化的鼻祖,于是他们又想到知识网可以从平行四边形出发,从整体上理解和掌握了知识之间的内在联系,感受了数学知识的逻辑性和系统性。
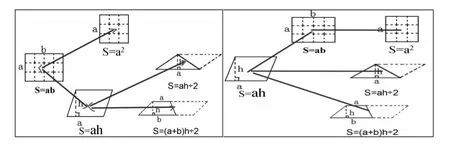
图4
(四)注重应用,在解决问题中感悟“知识价值”
复习课不应只是知识的简单重复呈现。在回顾与整理的过程中,它更多承载着沟通与生长的功能。沟通和生长的关键点在于提升练习,辅以教师的引导、点拨,为学生架构起“认知桥梁”,让学生感悟到知识间的碰撞、触发、再成长,从而实现关联学习,促进知识结构化的形成,让学生感悟知识的价值。
本课的应用环节中,学生很快就算出长方形、平行四边形、梯形、三角形的面积都是20平方厘米。教师提问:“为什么这些图形的面积都是20平方厘米?”通过对图形的分析、类比、联想,学生发现长方形和平行四边形面积相等是因为同底等高;三角形的底是10厘米,它是平行四边形底的2倍,高没变,但三角形的面积要除以2,所以面积也是20平方厘米;梯形可以通过割补法转换为底是10厘米,高是4厘米的三角形(如图5)。教师根据学生的成长,拖动图形,学生开始深入观察图形的内在联系,凸显图形本质的同时,也让梯形面积计算的万能公式的发现成为可能。
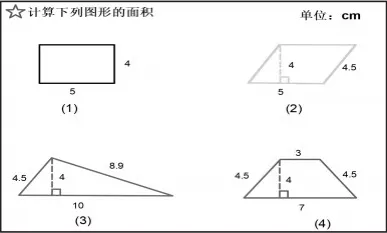
图5
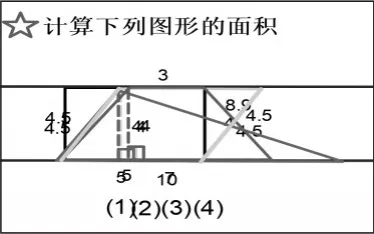
图6
接着,教师抛出更高层次的问题:“像这样,面积和高都不变的图形还有吗?”学生想象力迸发,创造了多种不同形状的等积梯形。教师捕捉到了学生创造出的上底是1,下底为9的梯形,让学生想象图形的形状,追问:“上底还能再小一点吗?”从整数自然就拓展成了小数,接着教师继续追问:“上底能不能继续小下去,直到……”打破梯形面积公式只能计算梯形面积的定式,沟通梯形与三角形的内在联系,丰富了梯形的内涵(如图6)。配合特定板书,学生继续开展运动想象,勾联了梯形与平行四边形的关系,然而这并不是结束,学生通过运动想象在得到倒三角形后惊喜地发现,当b=0时梯形的面积公式就变成了ah÷2,这就是三角形的面积公式,顺理成章的,他们又似乎发现a=b也可以推导出平行四边形的面积公式就是ah。学生在练习中发现知识网还可以以梯形为源头,结成一张新的网(如图7)。通过做这样的练习题,学生解决问题的思维从静态的基本图形组成分析上升到基于关系去分析图形之间的要素结构与等积变换,有效实现了知识间的关联与结构化。
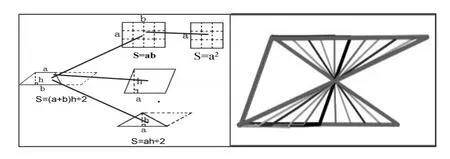
图7

