汝陰侯墓二號式盤地盤背面圖文新解

程少軒

《考古》1978年第5期公布了阜陽雙古堆西漢汝陰侯墓出土的3件式盤。(1)嚴敦傑： 《關於西漢初期的式盤和占盤》，《考古》1978年第5期，第334～337頁；殷滌非： 《西漢汝陰侯墓出土的占盤和天文儀器》，《考古》1978年第5期，第338～343頁。其中二號式盤，即被嚴敦傑先生稱爲“太一九宫占盤”者，《考古》所刊地盤背面綫圖及示意圖如下：(2)《考古》原刊線圖及示意圖均以“子夜半”在上、“日中”在下，這與古人占盤放置習慣不合。本文所用占盤圖像均改爲“子夜半”在下、“日中”在上。

殷滌非先生介紹説：

在背面，由中心點向四方劃出四個綫條，成一十字形。在各綫條末端分别針刻篆文“第一子夜半冬至右行”、“第二冬至平旦”、“第三七年辛酉日中冬至”(引者按： 殷文已指出“七年”爲漢文帝前元七年)、“第四冬至日入”。四隅劃“个”形，分刻“第二夏至”、“第三夏至”、“第四夏至”、“第四夏至”。……分冬至的那一天時刻爲四個等分，即“第一子夜半”，“第二平旦”，“第三日中”、“第四日入”。這就是説，第一年子夜半冬至，第二年是平旦冬至，第三年是日中冬至，第四年日入冬至，(3)許名瑲先生審閲本文初稿時補充説，此即《史記·曆書》“曆術甲子篇”所謂“正北，冬至加子時；正西，加酉時；正南，加午時；正東，加卯時”。子卯午酉二繩兩端標記時空，與此盤本質相同。這樣周而復始，統計一年的時間爲365日，四年而積一千四百六十一日。《淮南子·天文訓》説：“四歲而積千四百六十一日而復合故舍”，《後漢書·律曆志》也説：“日發其端，周而爲歲，然其影不復，四周千四百六十一日而影復初。”這占盤所揭示的冬至這一天，正好是經過四年日影復合如初。《天文訓》又説：“八十歲而復，故曰子午卯酉爲二繩，丑寅辰巳未申戌亥爲四鉤。”綜觀上述，這盤的方盤，亦與此正合。……《史記·律書》説：“天所以通五行八正之氣，”《索隱》“八謂八節之氣”。這占盤只言八節(引者按： 指該盤正面文字)，正與《史記》合；不言及二十四節，又與元光元年曆書注同。在八節中着重冬至和夏至(指這盤的背面專針刻冬至和夏至)，説明這兩個日期，在太陽周年視運動中有特殊的標誌，已爲古人所掌握。即冬至，遠極，故晷影長而晝短，“陰氣極，陽氣萌”，跨進了寒冷季節；夏至，北極近，故晷影短而晝長，“陽氣極，陰氣萌”，則進入炎熱季節。《淮南子·天文訓》説：“冬至加三日，則夏至之日也。歲遷六日而復始。”高誘注説：“冬至後三日，則明年夏至之日”；“遷六日，今年以子冬至，後年以午冬至也”。據這盤的八節，推算作下表。

表1 殷滌非所列文帝七年至十年八節干支

從表上看出，辛酉與甲子，丙寅與己巳，辛未與甲戌，都揭示按干支排列冬至加三日而爲當年夏至日，又歲遷六日正和辛酉到丙寅，丙寅到辛未，辛未到丙子之數。證明原著是對的。而注文説：“則明年夏至之日，”“今年以子冬至，後年以午冬至，”差誤甚大，原著“遷”字與“加”字，義有不同，高誘不加區辨，把它搞錯了。今以文帝七年的實物糾正高誘注，更可看出漢初天文觀測計算的精確。(4)殷滌非： 《西漢汝陰侯墓出土的占盤和天文儀器》，《考古》1978年第5期，第338～343頁。

按，殷滌非先生對盤中文字及曆法内涵的介紹大體準確，但所附表格的日期推算却頗有問題。現將殷文所列干支日期與我們推出的干支日列表對比如下：

表2 殷文與本文所推文帝七年至十年八節干支比較表

殷滌非先生所列表中干支日期有多處與我們所推之日相差一天。爲何會出現這種情況？經反復驗算，我們確認，殷先生應該是未能完全準確地理解該地盤背面文字的曆法内涵，加之自身演算亦有誤，致使出錯。(5)除了干支外，殷文文帝七年立秋之日期“七月初七”亦是誤算，實當作“七月初十”。本文初稿未校核序數日期，此承許名瑲先生驗算後指出，謹致謝忱！

在同期《考古》中，嚴敦傑先生也對該地盤背面文字作了討論：

地盤的背面是定四分曆冬至時刻數。四分曆冬至小餘開始是0，則第二冬至小餘1 /4=0.25，第三冬至小餘爲2 /4=0.50，第四冬至小餘爲3 /4=0.75。這就是盤上的夜半、平旦、日中、日入四個時刻的由來。又第三冬至後的夏至應該是第一夏至，因爲這夏至的小餘剛好是1 /8爲最小，以後第二夏至是3 /8，第三夏至是5 /8，第四夏至是7 /8也周而復始。第三冬至有“七年辛酉日中冬至”，用古四分曆推算漢文帝七年(公元前173年)冬至： 黄帝曆，癸亥25刻；夏曆，甲子75刻；顓頊曆，辛酉59刻；周曆，辛酉75刻；殷曆，壬戌50刻；魯曆，辛酉零刻。以顓頊曆所推爲近。又盤上冬至與夏至之間没有文字，按理這應該是春秋分，這樣從冬至到春分到夏至到秋分又到冬至便很順當了。(6)嚴敦傑： 《關於西漢初期的式盤和占盤》，《考古》1978年第5期，第334～337頁。

嚴敦傑先生指出冬至相關文字是説冬至小餘，這無疑是正確的。他認爲兩處“第四夏至”必有一誤，“第三冬至”後的“第四夏至”當改爲“第一夏至”，也是正確的。但後面所列夏至小餘的數據就有大問題了。我們以四個冬至之小餘爲定點，以第一冬至小餘=0，四分曆歲實365日，推算四個冬至、四個夏至小餘如下表：

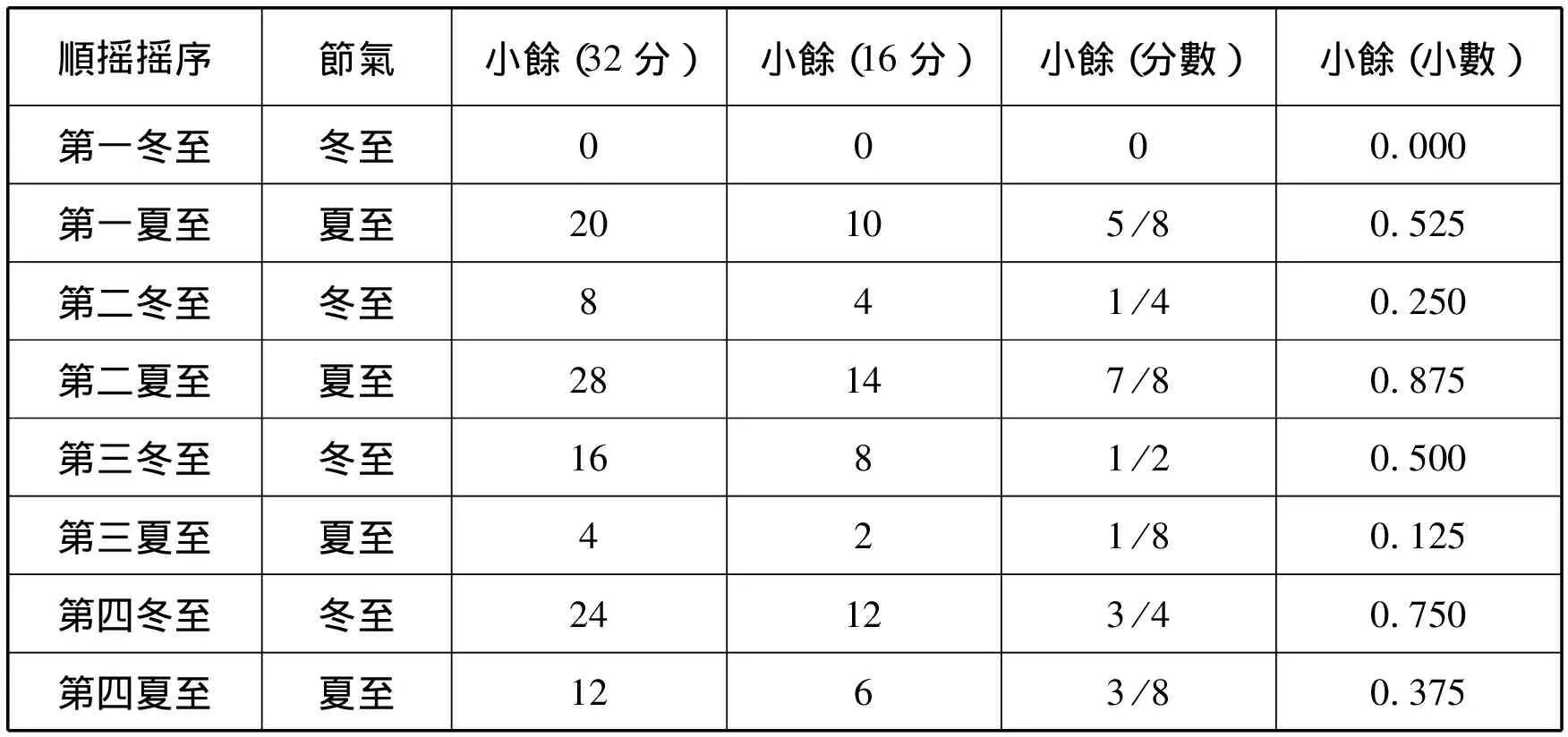
表3 汝陰侯墓二號式盤背面冬夏至小餘表

據上表可知，所謂“第一夏至的小餘剛好是1 /8爲最小，以後第二夏至是3 /8，第三夏至是5 /8，第四夏至是7 /8”的議論完全錯誤。第一夏至小餘不是1 /8而是5 /8；第二夏至不是3 /8而是7 /8；第三夏至不是5 /8而是1 /8；第四夏至不是7 /8而是3 /8。

正因爲嚴敦傑先生誤算了夏至小餘，所以未能進一步發現式盤的正確用法。下面我們根據背面更正後的示意圖，談談對此式盤的理解。

該圖的確如嚴敦傑先生所説，與節氣小餘有關。在更正了夏至小餘數據後，我們可以更進一步指出——式盤背面所繪圖像，就是用來推算冬夏至小餘，乃至推算冬夏至干支的。

以第一冬至子夜半小餘爲0起算(8)事實上秦漢時期並不存在整數“0”的概念，這裏嚴格來説應表述成“以第一冬至子夜半小餘爲16起算”，但這與現代數學的計算習慣不合。爲方便讀者理解，本文徑將達到取整進位狀態的小餘寫作“0”，後文不再一一説明。，取十六分制： 第一夏至小餘數爲10，正處第10道綫；繼續累加，第二冬至小餘累積爲20，進1日，所剩小餘數爲4，正處第4道綫；第二夏至小餘累積爲30，進1日，所剩小餘數爲14，正處第14道綫……其餘依此類推，綫之序數，即對應冬夏至之小餘。

雖然嚴敦傑先生列出的夏至小餘數據錯誤，但他推測“冬至與夏至之間没有文字，按理這應該是春秋分”，却又是正確的。只是嚴先生未能全然理解圖文的曆法内涵，也就無從指出這些綫條究竟如何代表春秋分。其實，方法與前面推算冬夏至一樣。冬夏至之間累加取數爲10，摻入它們的中點春秋分之後，累加數改取5，即每次數5道綫，就可以計算春秋分小餘了。我們可按十六分制小餘，列16道綫對應四組二分二至如下：

表4 四組分至小餘與羅圖十六綫對應關係表

依此術亦可方便推算出冬夏至干支。182日含3個甲子循環，餘2日。推算小餘時，滿1圈，即復至0號綫時，則小餘湊足整數進1日，累加在2日上，得餘數整3日。則前之冬夏至干支或加2日，或加3日，即下一冬夏至之干支日。例如上圖文帝七年冬至干支辛酉，爲第三冬至，則七年夏至日爲第三夏至，在2號綫，已過0號綫，所以當加3日，辛酉後3日爲甲子，即七年夏至干支。再推後一個冬至，八年冬至爲第四冬至，在第12號綫，未過0號綫，所以只加2日，甲子後2日爲丙寅，即八年冬至干支。

但是春秋分干支的計算，在此盤上就不便操作了。因爲它們距離冬夏至爲91又5 /16日，除去一個甲子後餘數30又5 /16日，餘數過大，無法便捷數得。這大概就是盤上不繪春秋分的原因。

稍有疑問的，是盤中“右行”二字。按文獻所見式盤操作的慣例，地盤中所謂“右行”一般是指逆時針運行，而圖中四個冬至的排列顯然是順時針的，依據逆時針完全無法操作。這或許是因爲文字與圖像在式盤的背面，依照操作者的視角，背面的逆時針運行就是正面的順時針運行。“左行”“右行”問題是數術研究中的一大難點，這篇小文本就無法説清楚。加之此二字的原始字形並未公布，實際情況究竟如何也無法判斷。因此，本文不再展開討論此問題，徑以“按示意圖順時針運行”理解式盤。

此種求冬夏至干支之法，與北大漢簡《節》篇冬夏至干支速算表十分類似。《節》篇簡31—32：

簡33—34有對該表的説明文字：

孝景元年，冬至庚寅。上八畫之下，即庚寅也。其次畫之下，亦夏至之日也。丹畫閒，閒一歲也。盡如此，以日次數之，每一畫一日也，終而復上，以爲常。

我們已在《北大漢簡〈節〉篇“冬夏至干支速算表”解讀》一文中闡述了以上圖文的使用方法。(9)程少軒： 《北大漢簡〈節〉篇“冬夏至干支速算表”解讀》，復旦大學出土文獻與古文字研究中心網站，http： / /www.gwz.fudan.edu.cn /Web /Show /2719，修訂後刊於《出土文獻與古文字研究》第7輯，上海古籍出版社，2018年，第355～359頁。第32簡4個“冬夏”，指的是4個連續的年份。4個年份用紅色綫條隔開，即簡文所謂“丹畫閒，閒一歲也。”我們將之自上而下編爲A、B、C、D四年。“冬”指對應横綫部分推算的是當年的冬至日干支；“夏”指對應横綫部分推算的是當年的夏至日干支。第31簡中黑色横綫，代表日期數，即“每一畫一日也”。4個年份分别有3+3、2+3、3+2、3+2條黑色横綫，合起來爲21日。四分曆歲實數爲365，4年共計360×4+5×4日=360×4+21日=1461日。360是六十甲子的倍數，可以整除，推算時不用考慮。剩餘21日不可整除，因此分配在4個連續的年份中——其中3個年份分配5日，一個年份分配6日。簡33、34説，“上八畫之下，即庚寅也”，是指B年冬至之格，自上起數第8道黑色横綫對應的干支日是庚寅。“其次畫”，指緊接着B年冬之格下面的3道黑色横綫。“其次畫之下，亦夏至之日也”，指要在前面庚寅日的基礎上，再加上3道黑色横綫代表的3個干支日，即癸巳日——這一天就是景帝元年的夏至日。按此算法，一個4年周期之中冬夏至干支日推算如下表所示：

表5 北大漢簡《節》篇冬夏至干支速算表推算法

按此推算方法，可以推算出漢初顓頊曆行用期間内各年份的冬夏至干支日。驗諸張培瑜先生《三千五百年曆日天象》，(10)張培瑜： 《三千五百年曆日天象》，大象出版社，1997年。推得冬夏至干支日期與之基本吻合。

可見，在古六曆時期，人們爲曆日推算發明了多種工具，汝陰侯墓二號式盤和北大漢簡《節》篇“冬夏至干支速算表”皆是其例。它們雖然形式迥異，操作方法也不太一樣，但本質都是利用了古四分曆參數的數學規律，均體現了古人的巧思，堪稱雙璧。

需要特别指出的是，細察汝陰侯墓二號式盤和北大漢簡速算表，雖然兩者所能推出的冬夏至干支並無不同，但兩者所據曆法其實是有細微差别的。北大漢簡速算表，所得冬夏至干支，與張培瑜先生《三千五百年曆日天象》吻合，而該書所用漢初顓頊曆節氣小餘，所據爲銀雀山漢簡元光元年曆譜等出土曆譜實物。因此，北大漢簡速算表所用節氣小餘參數，與元光元年曆譜完全一致。這一點，末永高康先生已經做了詳細考證，(11)末永高康： 《北京大學藏西漢竹書〈節〉の孝景元年冬至日をめぐって》，《出土文献と秦楚文化》第9號，2016年。所論當無疑義。

表6 據北大漢簡《節》篇速算表推元光元年及前後諸年份冬夏至干支

元光元年曆譜，冬至小餘爲11，立春小餘爲0，(12)張培瑜： 《新出土秦漢簡牘中關於太初前曆法的研究》，《中國古代天文文物論集》，文物出版社，1989年，第69～82頁。證明至少漢初官方行用之顓頊曆，節氣小餘所用參數，係以屬於D組年份的立春夜半齊同作爲起點的。(13)張培瑜先生認爲這一曆法的起點在“公元前672年5月甲子朔旦芒種夜半齊同”，實爲本文表述之特例，其曆法原理本質上並無不同。因涉及24節氣小餘具體推算，列表過長，兹不贅述。衆所周知，顓頊曆節氣小餘以立春爲起點，而古六曆的其他五種曆法，黄帝曆、殷曆、周曆、夏曆、魯曆，節氣小餘均是以冬至爲起點，這是顓頊曆與其他古四分曆的重要差異之一。因此，儘管與傳世文獻所反映的數據有所差别，但元光元年曆譜等出土漢初曆日實物以及北大漢簡《節》篇速算表，其陽曆部分均屬顓頊曆，應該是没有問題的。

而阜陽汝陰侯墓二號式盤，則顯然是以第一冬至子夜半齊同作爲起點的。這是其它五種古四分曆的特徵，與顓頊曆絶不相容。因此，在計算節氣時，據汝陰侯墓二號式盤和據顓頊曆，必然會有不同之處。我們以文帝五年至十年爲例，將汝陰侯墓二號式盤和漢初官方行用顓頊曆節氣小餘數據列表如下：

據上表，由於節氣小餘起算點不同，雖然兩種曆法推出的冬夏至干支完全一樣，但每四年立夏、秋分、立春的干支會有一日之别。而且，顓頊曆之冬夏至小餘，其32分制之數值恰逢奇數，所以也無法利用汝陰侯墓二號式盤推算——這也是曆法不兼容造成的。不過，利用同樣的原理，完全可以設計出一個可以推算顓頊曆立春、立夏、立秋、立冬四立小餘及立春、立秋干支的式盤。

漢初官方行用之顓頊曆，據D組立春小餘0爲起點，可上推曆元至乙卯。而汝陰侯墓二號式盤，據第一冬至子夜半爲起點，可上推曆元至甲寅，這與《開元占經》所載殷曆上元甲寅相合。且據此參數不可能推至黄帝曆上元辛卯、夏曆上元乙丑、周曆上元丁巳和魯曆上元庚子。再考慮到西漢前期殷曆的影響力僅次於官方行用的顓頊曆，因此我們認爲該式盤所據曆法極有可能是殷曆。

最後，需要附帶指出的是，地盤背面的曆法，與該盤正面講述的八節不屬於同一曆法體系。該盤正面相關文字如下：

冬=至=葉蟄卌六日廢明日。

立=春=天溜卌六日廢明日。

春=分=蒼門卌六日廢明日。

立=夏=陰落卌五日明日。

夏=至=上天卌六日廢明日。

立=秋=玄委卌六日廢日明。

秋=分=倉果卌五日明日。

立=冬=新洛卌五日明日。

李學勤先生指出這段文字與《靈樞·九宫八風》關係緊密，(14)李學勤： 《〈九宫八風〉及九宫式盤》，《王玉哲先生八十壽辰紀念文集》，南開大學出版社，1994年；收入《古文獻叢論》，上海遠東出版社，1996年，第235～243頁。記載的是八節相距的日數。文獻中這類八節相距日期的記載多見，李零先生曾列表詳加比較：(15)李零： 《北大漢簡中的數術書》，《文物》2011年第6期，第80～83頁。

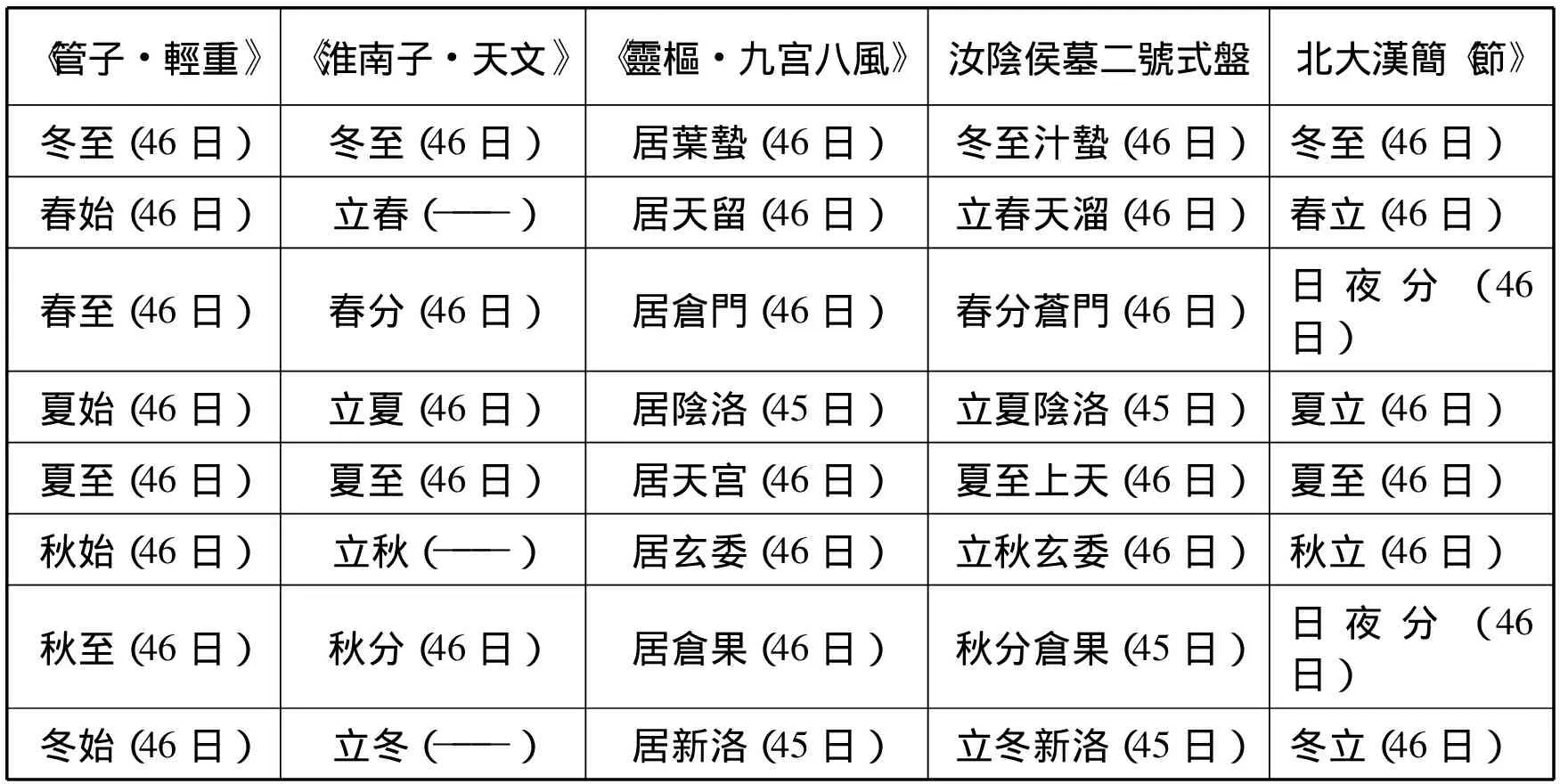
表9 文獻所見八節相距日期一覽

通過計算可知，根據四分曆八節小餘累進規律爲： 除了起算點(小餘零點)之後節點距日爲45日+46日排列外，其餘各節點距日均呈現45日+46日+46日循環排列的情況。以殷曆和顓頊曆兩種曆法的八節小餘累進爲例：

表10 殷曆八節小餘累進規律

表11 顓頊曆八節小餘累進規律

因此，依據四分曆實曆推出的八節距日，46日之時間段不可能連續出現3次，且45日之時間段不可能連續出現2次。以此結論驗諸表9，可知包括汝陰侯墓二號式盤在内的全部材料的八節日數，皆非據實曆推出。

阜陽雙古堆汝陰侯墓是1977年發掘的，發掘簡報、部分漢簡以及三件式盤於1978年秋季發表，倏忽已過去40年了。最初對式盤進行研究的殷滌非、嚴敦傑兩位先生，也已經逝世近30年了。作爲漢初列侯，雙古堆漢墓主人、第二代汝陰侯夏侯竃的食邑户數(六千九百户)遠高於軑侯利蒼、利豨(七百户)和沅陵侯吴陽(六百户)，甚至高於海昏侯劉賀(四千户)。因此，這個墓葬的考古價值是極高的。可惜的是，相較於同樣有40年發現歷史的長沙馬王堆漢墓和隨州曾侯乙墓，汝陰侯墓未免顯得冷清。2018年初冬之際，謹撰此小文，作爲對汝陰侯墓出土資料發表40週年的紀念。