以“确定特殊三棱锥外接球球心及线面垂直的垂足”为例论直观想象能力的培养

赖志生

数学学科的本质与功能目标，也就是育人价值，其功能目标用史宁中教授的话来诠释是最恰当不过的，即“让学生会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界”.

新课程标准明确要求，数学教学要将培养学生的数学核心素养当作课堂教学的重要目标，着重培养学生的数学学科能力，塑造学生的个人品质，使学生适应社会发展. 高中数学核心素养主要包括数学抽象、逻辑推理、数学建模、数学运算、直观想象以及数学分析六个方面.在教学的过程中，教师应该结合学生数学核心素养的培养，有效设计教学方案，促进学生数学能力的提升.

在立体几何的教学活动中，寻找特殊三棱锥外接球的球心，进而求半径以及特殊三棱锥体高、线面角计算时寻找垂足的位置，学生都觉得相当困难. 恰恰这些都是高考的热点问题，既考查学生的空间想象能力和运算求解能力，同时也考查了学生运用化归思想的能力，题目难度为中等或偏难. 本文以这两个常见问题为例，探讨在解决问题过程中如何培养学生的“直观想象”这个数学核心素养.

一、寻找球心问题

以下是课堂教学过程中的例题设计：

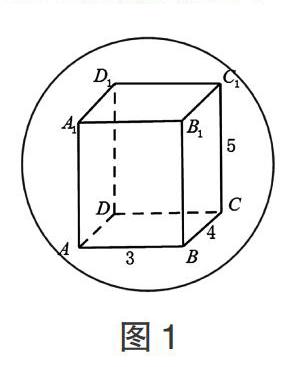
例1：若长、宽、高分别为3、4、5的长方体ABCD-A1B1C1D1的各个顶点都在球面上，则这个球的表面积为_____.（图1）

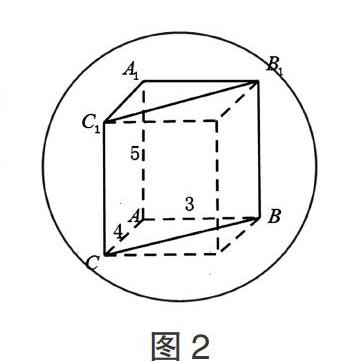
例2：直三棱柱ABC-A1B1C1的各个顶点都在同一球面上，AB=3，AC=4，AA1=5，AB⊥AC，则这个球的体积为         .（图2）

例3：已知三棱锥S-ABC，SA⊥AB、SA⊥AC、AB⊥AC，且AB=3、AC=4、SA=5，则该三棱锥外接球的表面积为         .（图3）

例4：三棱锥S-ABC，SA⊥平面ABC、AB⊥BC、BC⊥SB，且AB=3、BC=4、SA=5，则该三棱锥外接球的体积为         .（圖4）

例5：在四面体ABCD中，AB=CD=5、AD=BC=■、AC=BD=

3■，其外接球的表面积为         .（图5）

在以上5个例题中，学生比较容易看出后四个几何体都是以长方体为模型，可把它们嵌入长方体，通过补形法确定球心位置，求出半径后再求出表面积或者体积. 当我们把棱长改成相等时，学生马上就会想到这些几何体都是以正方体为模型，特别是经常考查的正四面体外接球问题. 不少学生在寻找球心位置的时候感到非常困难，无从下手，主要原因就是直观想象能力不强. 这样设计系列问题的目的，就是为了把学生经常遇到的各种特殊三棱锥和长方体相结合，培养他们的直观想象能力.

对于某些三棱锥外接球问题，在确定球心位置时还可以用轴截面法，这种方法同样能很好地培养学生的直观想象能力.下面以上述例3为例：

第一步：先确定底面△ABC外接圆圆心. 因为△ABC是直角三角形，故其外接圆圆心在BC的中点处，设为O1，半径r=■.

第二步：过O1作小圆圆面的垂线，则球心O必在该线上，且OA=OB=OC.

第三步：作出轴截面，即矩形SAO1P，球心O在O1P上，且只需OS=OA，显然球心O就是O1P的中点，再在■中由勾股定理就可以算出球的半径.

例6：已知三棱锥S-ABC，SA⊥AB、SA⊥AC、∠BAC=120°，且AB=3、AC=4，SA=5，则该三棱锥外接球的表面积为         .（例3改编）

当我们把∠BAC=90°改成120°时，显然不适合补形法，故对这种题型我们仍可以用轴截面法.

第一步：先确定底面△ABC外接圆圆心O1. 虽然不再是直角三角形，但是我们可以先用余弦定理，再用正弦定理求出外接圆半径r=■.

第二步、第三步与上述相同.

通过以上几个例题，想必不少学生对特殊三棱锥外接球问题的处理有了基本的思路. 当然还有许多特殊几何模型可以帮助确定球心，同时也可以通过建立空间直角坐标系，直接求出球心坐标进而求出半径. 在建立坐标系的过程中同样能很好地培养学生的空间想象能力，这里就不再赘述.

二、寻找垂足问题

在作线面垂直时，如何确定垂足的位置同样是学生的一大难点. 对于特殊三棱锥，笔者发现几乎都满足以下三个特征之一：①直接有线面垂直;②没有线面垂直但有面面垂直;③如果以上两个特征都没有，那么该几何体（或者几何体部分）具备对称性.

例7（2017年高考数学全国卷3文科）：如图，四棱锥P-ABCD中，PA⊥平面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点.（Ⅰ）证明MN∥平面PAB;（Ⅱ）求四面体N-BCM的体积.

显然这道题具备“直接有线面垂直”的特征，这类问题最简单，往往给出的条件是侧棱垂直于底面. 又N为PC的中点，所以在需要作四面体N-BCM的高时，过点N作平行于PA的直线交AC于点E，那么必有NE⊥底面BCM，且点E是AC的中点，NE=■PA. 故可充分利用线面垂直这个条件，可以直接用，也可以借用.

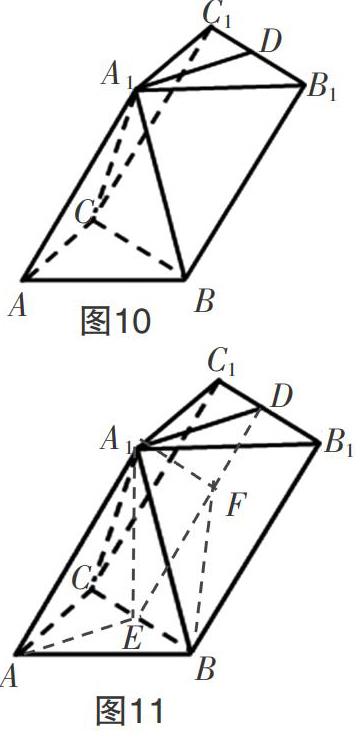
例8（2015年高考数学浙江卷文科）：如图，在三棱锥ABC-A1B1C1中，∠BAC=90°，AB=AC=2，AA1=4，A1在底面ABC的射影为BC的中点，D为B1C1的中点.（1）证明：A1D⊥平面A1BC;（2）求直线A1B和平面BB1C1C所成的角的正弦值.

在第二问求线面角时，同样需要作线面垂直，确定垂足的位置. 这道题既没有特征①也没有特征②，但是仔细观察，我们就会发现该几何体具备对称性（特征③）. 我们作个截面A1DEA（如图11），把这个几何体对半分，必有截面A1DEA⊥平面BB1C1C，且截面A1DEA∩平面BB1C1C=DE. 也就是说这道题转化为了具备特征②的题目，故我们只需过A1作A1F⊥DE于点F. 由上，我们轻易就能证明点F就是垂足，连接BF，则∠A1BF就是所求角（如图11）. 教师在讲解这类题时，可以出示一些具体简单的具有对称性结构的几何体，先让学生好好感受作对称截面会得到面面垂直的情况，培养他们的直观想象能力，然后再进行证明.

注：本文作者系广东省严运华名教师工作室成员.

责任编辑   罗 峰