带环形刚性隔板和基础隔震储液罐的动力响应
王成龙,王佳栋,孙保苍,王 丹
(1.江苏大学 土木工程与力学学院,江苏 镇江212001; 2.解放军陆军工程大学,南京210007)
储液罐是石油和天然气等资源储存的重要设施,储液罐中流体在外力激励下产生的晃动往往会导致结构的失稳和破坏[1]。工程中,常用隔板来控制储液罐中流体的晃动,实验表明隔板可以有效地改变储液罐中流体的自由晃动特性,增大流体晃动的阻尼,有效地减小流体受迫晃动时的波高响应,其中以环形隔板的应用最为广泛[2-5]。基于流体子域法,研究了水平激励下带多层刚性隔板的圆柱形储液罐的动力响应,通过对液动压力在流-固耦合界面的积分,详细探讨了液动压力所产生的基底剪力和倾覆力矩[6-7]。基础隔震储液罐的理论研究常采用质量和弹簧组成的等效力学模型。目前我国储液罐抗震鉴定标准所采用的就是Haroun 等提出的等效力学模型,该模型将流体等效为对流质量,柔性脉冲质量和刚性脉冲质量[8]。国内外专家基于该模型分别研究了各种隔震装置的减震效果和隔震机理,指出隔震装置能够有效降低基底剪力和倾覆力矩,但是对减小流体晃动波高响应的作用不大[9-14]。
根据国内外研究可知,基础隔震装置可以降低基底剪力和倾覆力矩,隔板可以减小晃动波高,但是关于隔板与隔震支座的综合防护机制的研究甚少。因此,文中以带环形刚性隔板和基础隔震的圆柱储液罐为研究对象,建立其动力响应方程,并通过地震响应的结果分析隔震支座和隔板参数对基底剪力和倾覆力矩的影响,所得结论将会为大型石油储液罐的防灾减灾设计提供重要的依据。
1 流体晃动解析模型
考虑如图1(a)所示的带有环形隔板圆柱形储液罐,其中罐壁、罐底均为刚体,环形隔板为内边自由、外边固支的刚性薄板。流体为无黏、无旋、不可压缩的理想流体。储液罐内径为R2,环形隔板内径为R1,自由液面到罐底的距离为H,隔板到罐底的距离为z1,隔板厚度可以忽略不计。按图1(a)所示建立坐标系,储液罐相对于地面的位移为x0(t),地面相对于惯性系位移为xg(t)。通过柱坐标分析储液罐中流体和罐体的运动,并采用子域法将储液罐中的流体区域分割成4个子域Ωi(i=1,2,3,4),如图1(b)所示。
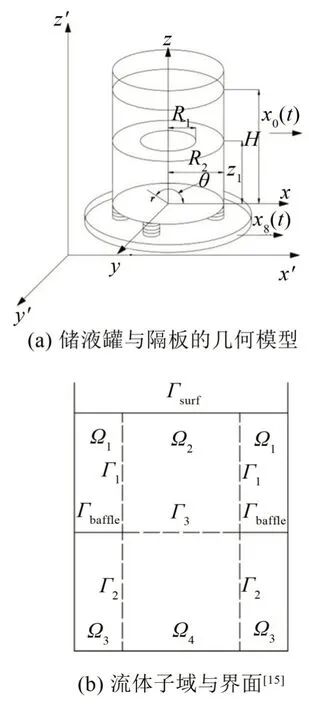
图1 储液罐的几何模型和流体子域划分
流体密度为ρ,子域内Ωi(i=1,2,3,4)的速度势[2]为φi(r,θ,z,t)。根据势流理论,储液罐中流体的速度势函数应该满足拉普拉斯方程

储液罐的初始条件和边界条件为[15]

式中:ηi为流体子域Ωi(i=1,2)的自由液面的波高方程,由文献[15]可得
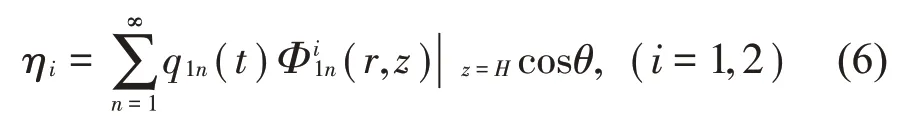
式中:q1n(t)为关于时间广义坐标,Φi1n为带刚性隔板圆柱形储液罐中的晃动模态,其对应的晃动的固有频率为ω1n。
在自由液面处,根据流体速度和势函数的关系得

由参考文献[15]可将流体速度势函数设为

式中:R1n(t)为关于时间广义坐标。
可以将式(6)和式(8)代入式(7)中得
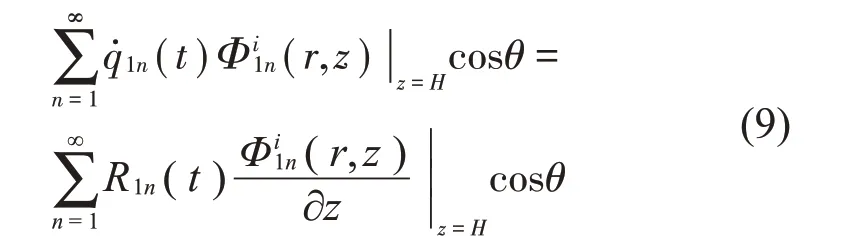
由流体自由晃动模态的正交性[15]得
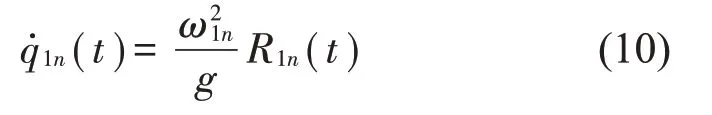
2 考虑基础隔震的动力响应方程
将式(6)、式(8)和式(10)代入自由液面方程式(4)中得

引入以下无量纲的量

将无量纲的量代入式(11)中,并由流体自由晃动模态的正交性得
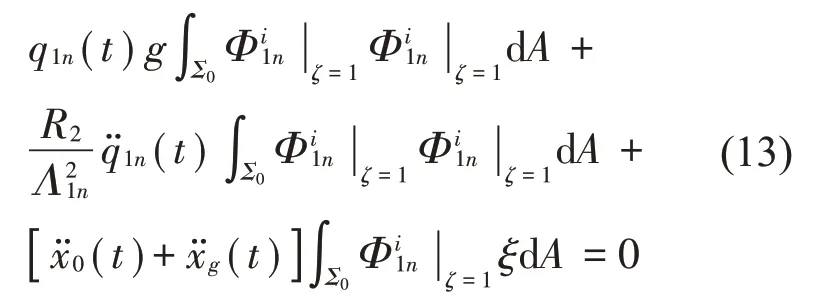
将式(13)简化得
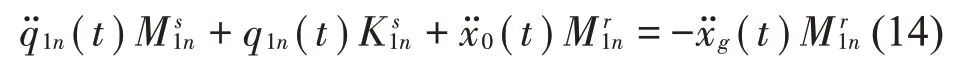
式中:
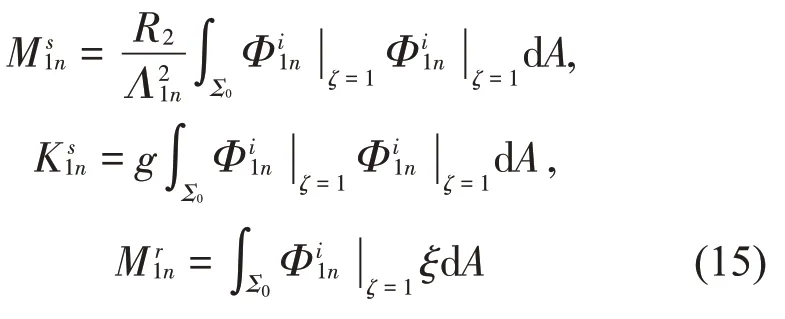
根据伯努利方程,储液罐中流体晃动所产生的液动压力为

沿着储液罐的侧壁,将式(16)进行积分即可得到流体对储液罐侧壁的合力,也就是作用储液罐地基上的基底剪力,在此考虑当激励沿θ=0的方向时,流体对储液罐侧壁的合力为

利用相同的积分方法可得到作用在储液罐罐壁上的液动压力所产生的倾覆力矩为
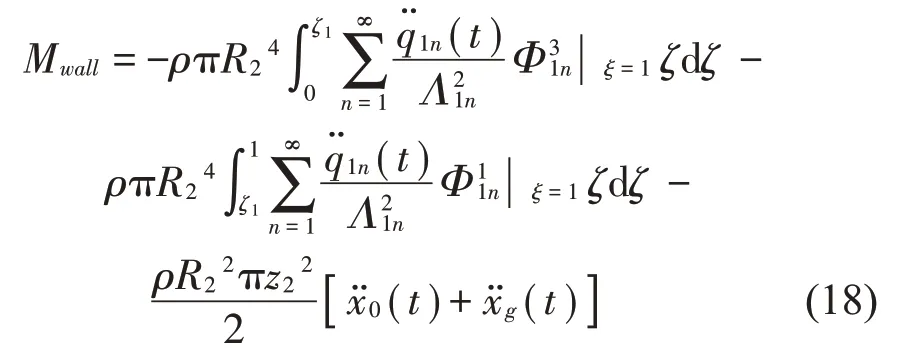
作用在隔板上下表面上的液动压力所产生的倾覆力矩为
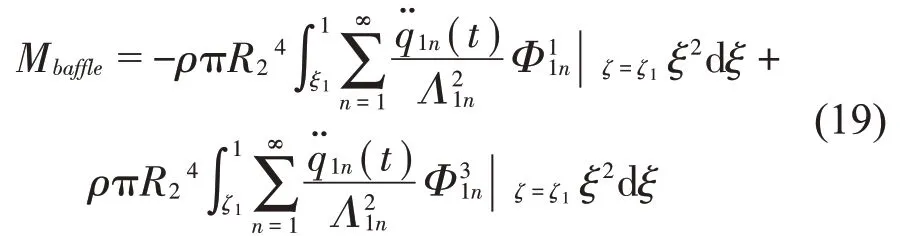
作用在储液罐罐底的液动压力所产生的倾覆力矩为

由式(18)、式(19)和式(20)可得到作用在整个储液罐上的倾覆力矩为
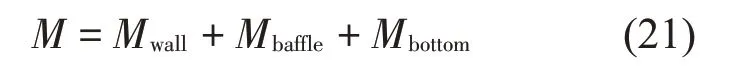
考虑储液罐的隔震,并根据达朗贝尔原理,建立动力学方程为
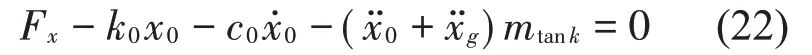
式中:k0=ω20ML为隔震刚度,c0=2ξ0ML为隔震阻尼,ML储液罐中流体的质量,ω0为基础隔震频率,ξ0为隔震层的阻尼比,取ξ0=0.2[16]。
将式(17)代入式(22),并忽略储液罐罐体质量mtank,从而将式(22)简化为

式中:
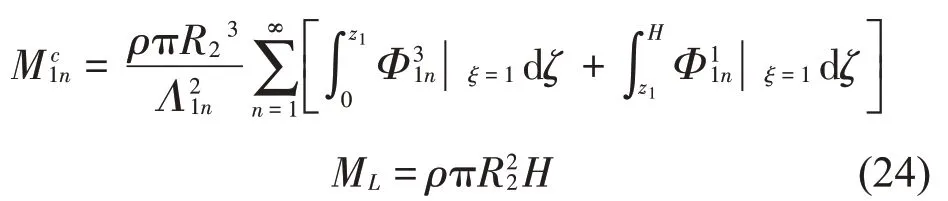
由式(14)和式(23)可得动力响应方程
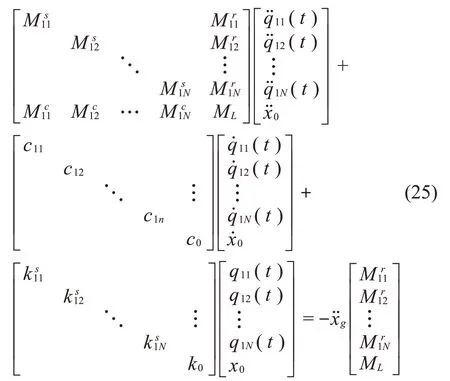
3 验证和参数研究
采用Newmark-β方法求解方程式(25)。输入水平方向的激励,选取南北方向的Kobe 地震波,时间间隔为0.02 s,持续时间为30 s,最大加速度绝对值为0.98 m/s2。
图2给出了Kobe 波的时程曲线。储液罐的内径R2=1.0 m,液面高度H=1.0 m,储液罐中流体密度ρ=103kg/m3。
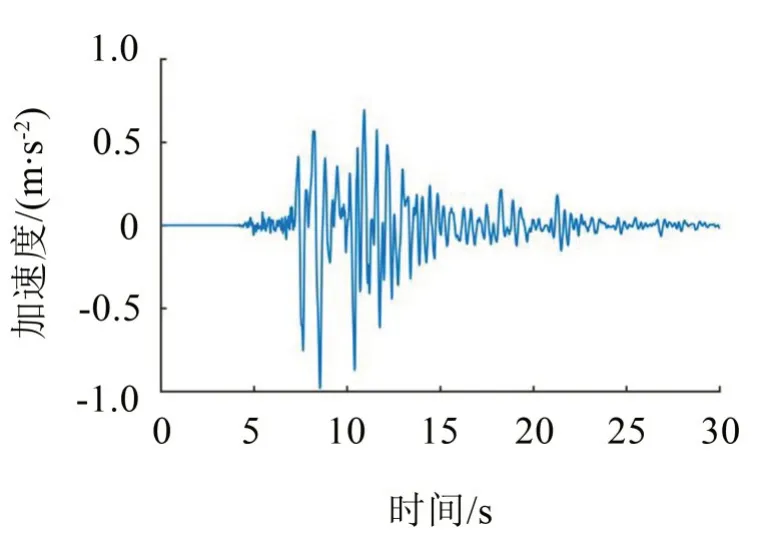
图2 Kobe地震波时程曲线
3.1 方法验证
当隔震支座周期很小时,隔震支座接近于刚性,此时带隔板和基础隔震储液罐的动力响应接近于无隔震的情况[15]。隔板内径取为R1=0.5 m,隔板位置取为z1=0.5 m,隔震支座的周期取为T0=0.2 s。
由图3显而易见:带隔板和基础隔震储液罐的基底剪力和倾覆力矩结果与无隔震的结果基本吻合,验证了该动力响应方程的正确性。
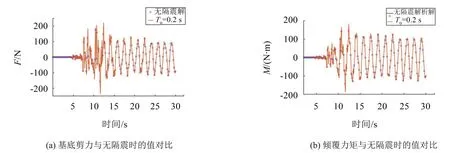
图3 T0=0.2 s时基底剪力和倾覆力矩与无隔震时的结果对比
3.2 隔震周期对减震效果的影响
隔板内径取为R1/R2=0.5,隔板位置取为z1/R2=0.5。从图4可看出:随着隔震支座的周期T0增大,储液罐的基底剪力和倾覆力矩的峰值均呈现先增大后减小的趋势。其中基底剪力和倾覆力矩的峰值在T0=0.4 s 取得最大,这主要是因为此时的隔震支座周期接近于一般土层下Kobe 地震波的卓越周期,地震响应被明显放大。当隔震支座的周期T0=0.9 s 时,基地剪力的峰值等于无隔震基地剪力的峰值,倾覆力矩峰值略小于无隔震倾覆力矩峰值。
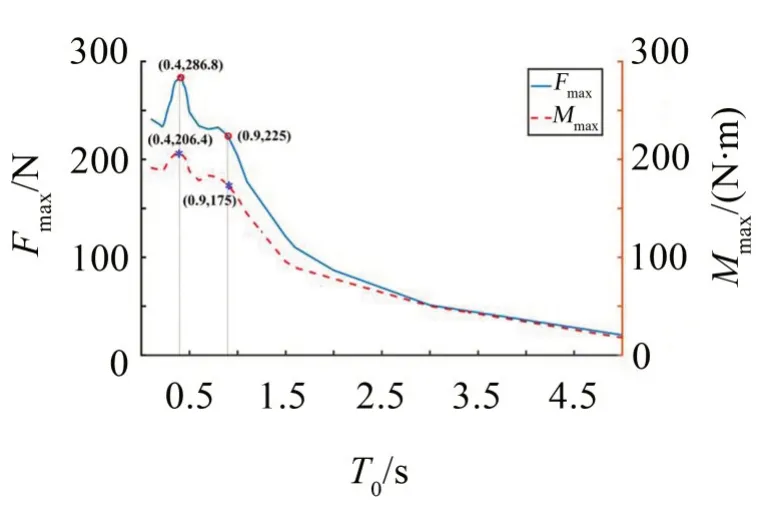
图4 隔震支座周期对减震效果的影响
因此,当隔震周期T0>0.9 s时,隔震支座可起到减震作用,并且减震效果随着隔震周期的增大而增大。
3.3 隔板内径对减震效果的影响
隔板位置取为z1/R2=0.5,考虑4 个不同的隔震支座周期,分别为T0=0.5 s、0.8 s、1.0 s和1.2 s。从图5(a)可看出:随着隔板内径的增大,储液罐的基底剪力峰值呈现先减小后增大的趋势。当隔板内径较小时,刚性质量所产生的晃动力远大于对流质量所产生的晃动力;随着隔板内径的增大,刚性质量产生的晃动力逐渐减小,对流质量产生的晃动力在逐渐增加,这两者具有相反的相位,因此整体的基底剪力峰值呈现出先减小后增大的趋势。
从图5(b)可看出:随着隔板内径的增大,储液罐的倾覆力矩峰值呈现增大趋势。当隔板内径较小时,对流质量的压力中心到罐底的距离较大,所以对流质量所产生的力矩大于刚性质量所产生的力矩;随着隔板内径的增大,对流质量所产生的力矩逐渐增大,刚性质量产生的力矩逐渐变小,这两者具有相反的相位,因此整体的倾覆力矩峰值呈现出逐渐增大的趋势。
3.4 隔板位置对减震效果的影响
隔板内径取为R1/R2=0.5,考虑4个不同的隔震支座周期,分别为T0=0.5 s、0.8 s、1.0 s和1.2 s。
从图6(a)可看出:随着隔板位置的增高,储液罐基底剪力的峰值呈现先减小后增大的趋势。当隔板位置较低时,刚性质量所产生的晃动力小于对流质量所产生的晃动力;随着隔板位置的增高,刚性质量产生的力逐渐增大,对流质量产生的晃动力逐渐减小,这两者具有相反的相位,因此整体的基底剪力峰值呈现出先减小后增大的趋势。
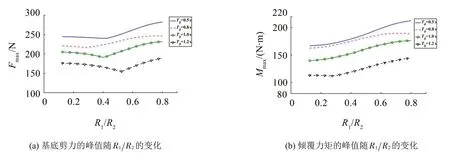
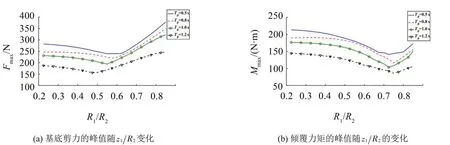
图6 隔板位置对减震效果的影响
从图6(b)可看出:随着隔板位置的增高,储液罐的倾覆力矩峰值呈现先减小后增大的趋势。当隔板位置较低时,对流质量所产生的力矩远大于刚性质量所产生的力矩;随着隔板位置的增高,刚性质量产生的力矩逐渐增大,对流质量产生的力矩逐渐减小,这两者具有相反的相位,因此整体的倾覆力矩峰值呈现出先减小后增大的趋势。
4 结语
(1)建立带环形刚性隔板和基础隔震的圆柱形储液罐的动力响应方程,并验证了该动力响应方程的正确性。
(2)当隔震支座周期T0>0.9 s 时,隔震支座可起到减震的效果,并且隔震支座的周期越大,隔震支座的减震效果越好。
(3)当隔震支座周期0.5 s ≤T0≤1.2 s 时,随着隔板内径的增大,储液罐的基底剪力的峰值呈现先减小后增大的趋势,而储液罐的倾覆力矩的峰值呈现不断增大的趋势。
(4)当隔震支座周期0.5 s ≤T0≤1.2 s 时,随着隔板位置的增高,储液罐基底剪力和倾覆力矩的峰值均呈现先减小后增大的趋势。

