瓦屋山引水隧洞围岩流变特性数值分析
王兆强,陈 新,张 磊,朱文凯
(四川大学水利水电学院,成都 610065)
0 引 言
在水利工程建设中,常常通过引水隧洞实现水资源跨流域、跨区域建设。引水隧洞开挖后围岩变形受开挖空间和时间效应的影响,呈强非线性变化,建立不同类别围岩的时效变形预测模型对工程设计和维护具有重要意义。变形预测的方法较多,但针对引水隧洞围岩运行期围岩变形预测的研究仍较少。金长宇等[1]建立了ANFIS模型来预测龙滩水电站地下厂房施工期的变形;张倩等[2]采用遗传算法优化BP神经网络,结合动态分析法建立了施工期围岩变形预测模型。目前传统预测模型注重对监测数据本身规律性的拟合,忽视了围岩变形的力学机制,此类预测模型会随着围岩应力状态的改变而失效,常常用于短期预测,为临时支护结构的设计提供依据。
鉴此,本文针对砂岩的流变特性,采用Burgers模型反映其流变变形规律,基于现场位移监测资料,通过遗传算法优化的BP神经网络对模型中的力学参数进行反演,利用参数化程序设计语言编写Burgers 流变方程并接入通用有限元软件ANSYS模拟隧洞岩体充水运行条件下的流变力学行为,取得了良好的应用效果。
1 工程地质条件
瓦屋山水电站枢纽位于洪雅县炳灵乡,枢纽由拦河大坝、左右岸泄洪隧洞、引水系统和厂房等建筑物组成。其中引水系统包括引水隧洞、调压井和埋藏式压力管道。引水隧洞主洞长4 765.322 m,断面为圆形,内径6.2 m,衬砌厚度40~80 cm。据地勘资料,洞周围岩类型包括:Ⅲ类围岩,长3 260 m,桩号0+239.97~3+499.97,以巨厚层~中厚层砂岩为主,部分薄层砂岩泥质岩类;Ⅳ类围岩,长1 425 m,桩号0+079.97~0+239.97、3+499.97~4+439.97、4+499.97~4+825.292,以中厚层泥质粉砂岩或中厚层粉砂质泥岩夹薄层粉砂质泥岩或泥质粉砂岩为主;Ⅴ类围岩,长140 m,桩号0+000~0+079.97;4+439.97~4+499.97,风化及卸荷的中厚层泥质粉砂岩夹薄层粉砂质泥岩。Ⅲ、Ⅳ类围岩中尚局部存在Ⅴ类围岩,主要岩体力学参数见表1。

表1 引水隧洞围岩分类及岩体力学参数建议值Tab.1 Classification of surrounding rock of diversion tunnel and suggested values of rock mass mechanical parameters
2 围岩变形监测结果
图1给出了隧洞收敛监测断面测点、测线的布置。结合工程地质和施工条件,确定施工监测方案以洞周收敛和锚杆应力监测为主。其中变形监测断面按照分段控制的原则,在Ⅲ、Ⅳ类围岩洞段选择6个变形监测断面,在开挖近掌子面的设计断面上埋设测点,测点按照圆形断面5测点8测线进行布置。本文根据固定点任意三角形法计算得出引水隧洞围岩测点的位移。固定点任意三角形法假设:周公河侧测点5处于坐标原点且不发生变形;测点1和测点5处于相同水平位置,测点1只作水平方向变形;测点2、测点3和测点4的变形分解为水平和竖直两个方向位移。
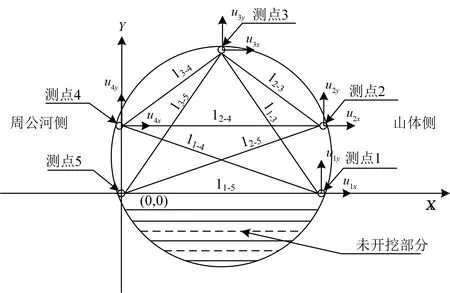
图1 隧洞收敛监测断面测点、测线布置图Fig.1 Tunnel convergence monitoring section measurement point, line layout
本文选取1号支洞下游面的第二断面(K1+90)作为研究对象,原因包括:该断面岩石为Ⅲ类围岩,在三类主要的围岩中占比到达69%,具有一定的代表性;该断面监测设备埋深时间为2005年8月16日,监测时间长达2个月,监测数据充足;期间断面开挖活动停止后只进行临时支护,期间围岩应力状态变化不大,易于模拟分析;开挖活动停止后各测线收敛值仍在增加,砂岩的流变特性得到充分表现,有利于对围岩流变参数的反演分析。
图2给出了1号支洞下游面的第二断面5个测点收敛值,基于固定点任意三角形法假设测点5处于坐标原点且不发生变形故不在图中列出。分析位移监测值可知,监测断面整体向周公河侧变形,主要由于靠山侧围岩的侧向压力和水压力较大。
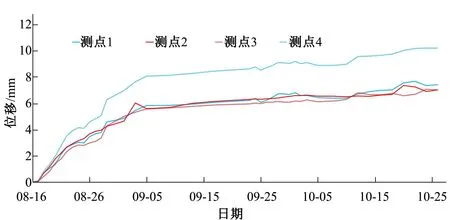
图2 测点位移监测值(2005年)Fig.2 Measuring point displacement monitoring value
3 砂岩本构模型及力学参数
王志俭等[3]通过对砂岩岩石和岩体进行流变试验和分析,认为Burgers 流变模型可以准确描述砂岩的流变特性。Burgers 流变模型为四元件两单元模型,在三轴应力条件下,该模型的轴线应变表达式为:
(1)

式中:G2为黏弹性剪切模量;η1为黏性系数;η2为黏弹性系数;K为体积模量;G1为剪切模量;E1为弹性模量;η为泊松比。
其中η1、η2、E1和G2四个力学参数需要通过参数反演确定。根据地质资料、三轴试验成果以及工程经验综合确定确定出了四个参数取值范围,见表2。

表2 反演参数取值范围Tab.2 Inversion parameter value range
4 围岩力学参数反演
4.1 遗传算法优化的BP神经网络模型
通过MATLAB对遗传算法优化的BP神经网络模型进行设计和编程,网络模型的建立主要分为以下两个部分。
(1)遗传算法优化BP神经网络。 基于BP神经网络,采用遗传算法进行全局搜索,得到BP神经网络最佳阈值和初始权值,再将优化后的阈值、权值输入BP神经网络,神经网络的局部搜索功能可以快速获得近似最优值。遗传算法的优化解决了BP神经网络易陷入局部极小值、稳定性差与网络收敛慢的问题。
(2)拟定神经网络结构。BP神经网络的结构包括的输入层、输出层和隐含层,其中输入层与输出层节点数根据实际问题确定,而隐含层节点数N可以通过公式(3)确定。通常先拟定一个初始值用于BP神经网络训练,若训练的结果不满足要求,则增加一个隐含节点直至满足要求。
(3)
式中:a为1~10之间的常数;m、n分别为输入层节点数和输出节点数。
通常先拟定一个初始值用于BP神经网络训练,若训练的结果不满足要求,则增加一个隐含节点直至满足要求。
根据BP神经网络结构的布置要求,以待反演力学参数作为神经网络的目标向量,输出节点数为4;以位移监测收敛值作为BP神经网络的输入向量,输入节点数为280。根据公式(3)隐层节点数初始值拟定为20层。
4.2 训练神经网络样本
训练神经网络样本是一个不断寻找最佳阀值与权值的过程,即通过训练使得网络的输出误差越来越小。本节拟利用Levenberg-Marquardt算法对神经网络样本进行训练。
基于均匀设计法[4],选用U11(117)均匀设计方案对前文四个力学参数η1、η2、E1和G2进行试验设计组合,得到11组不同组合的参数。通过数值分析模拟计算11组力学参数分别对应的测点位移值,具体模拟过程可以参考第六节。
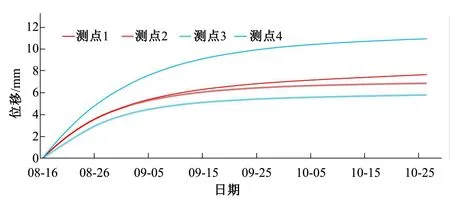
图3 神经网络训练样本(2005年)Fig.3 Neural network training samples
11组力学参数和对应的测点位移值共同组成人工神经网络的训练样本,为力学参数反演提供初始样本,由于篇幅有限,仅列出η1=1.03×1018、η2=1.21×1016、E1=39和G2=9.80×1010组合时的训练样本以供参考,见图3。采用初次训练好的网络样本进行参数反演,可能由于样本数量偏少而不能满足工程要求,可以继续增加网络训练样本,直至得出合理的反演参数。
4.3 力学参数反演及合理性验证
通过MATLAB对遗传算法优化的BP神经网络法进行设计和编程,将K1+90监测断面5个测点70 d监测值作为输入向量导入初始训练样本中,输出四个力学参数,结果为:η1=7.13×1017、η2=1.27×1016、E1=39、G2=1.80×1011。
将反演参数导入计算模型中,通过数值模拟得到K1+90断面各测点70 d的流变位移,图4给出了位移计算值与监测值得对比结果,各测点计算结果与监测数据拟合度较好,相对误差基本控制在10%以内,符合工程需要。因此Burgers流变模型和力学参数可以较好的描述该水电站砂岩地层引水隧洞1号支洞下游面围岩流变特性,可以用于引水隧洞围岩运行期变形预测。

图4 计算位移值和监测值对比分析(2005年)Fig.4 Comparison of calculated displacement values and monitored values
5 隧洞运行期稳定性预测
5.1 建立计算模型
利用参数化程序设计语言编写Burgers 流变方程并接入通用有限元软件ANSYS,程序每次迭代计算时均调用一次APDL,并更新应力和应变,从而实现砂岩流变模型的导入。
由于引水隧洞沿轴线方向较大范围内围岩岩性单一,因此,该问题可简化为平面应变问题。为减少边界效应,网格模型上下边界的设定均大于洞径的10倍,已知引水隧洞1号支洞下游面断面为圆形,内径6.2 m,衬砌厚度为0.6 m,因此模型计算范围为80 m×80 m,围岩和衬砌模拟单元均采用平面单元Plane42。模型有限元网格如图5所示。

图5 模型有限元网格Fig.5 Model finite element mesh
模型边界条件及初始条件:左右两侧、底部均采用法向约束;初始应力场以自重应力场为主;外水压力对引水隧洞的围岩和衬砌结构的长期稳定性有较大的影响,因此应当考虑外水压力对隧洞的影响,根据工程地质报告,对隧洞模型顶部施加80 m的压力水头,底面施加160 m的压力水头,侧面施加沿重力方向梯度变化的压力水头。
给定初始应力场和外水压力的模拟完成后,依次进行隧洞全断面开挖模拟及隧洞支护模拟(初期采用喷混凝土、挂网、锚杆支护)。由于开挖与衬砌施作之间的间隔时间较长,围岩变形量较大,开挖与衬砌施作期间及竣工之后还需要进行蠕变模拟。经过上述施工模拟建立运行期的初始应力场,在此基础上施加运行期的内水压力,最后分别对隧洞充水运行初期(流变时间为T=0 d)、T=10 d、T=30 d、T=60 d、T=120 d、T=240 d,T=360 d不同时段的流变情况进行模拟,每次流变模拟均调用Burgers 流变模型,并更新应力和应变,进而对引水隧洞长期的稳定性进行评价。建立围岩流变模型所需的力学参数η1、η2、E1和G2通过上述参数反演已经确定,其余计算所需的力学参数见表3。
5.2 计算结果分析
图6、图7给出了隧洞充水运行期流变时间T=60 d和T=360 d的位移场云图。隧洞运行T=60 d后,从位移的Y分量和位移的X分量云图可以看出:隧洞顶拱变形方向向下,Y方向最大位移分量为3.316 1 mm;底拱变形方向向上,Y方向最大位移分量为2.131 7 mm;山体侧隧洞水平位移分量要大于周公河侧,均向左侧发展变形,X方向最大位移分量为5.661 8 mm。
隧洞运行一年T=360 d,与隧洞运行60 d的位移情况相比发现:隧洞顶拱继续向下变形,Y方向最大位移分量达到3.836 1 mm;底拱发生少量回弹变形,变形方向向下,Y方向最大位移分量减小为2.001 2 mm,位移方向向上;山体侧隧洞水平位移分量仍大于周公河侧,继续向左侧发展变形,最大位移分量为达到5.661 8 mm;位移增量较小,流变变形处于收敛状态。

图6 T=60 d围岩及衬砌位移云图Fig.6 T=60 d displacement cloud chart of surrounding rock and lining

图7 T=360 d 围岩及衬砌位移云图Fig.7 T=360 d displacement cloud chart of surrounding rock and lining
为了系统分析引水隧洞1号支洞下游面围岩的流变规律,对不同时刻的位移云图进行整理,得到对应时刻围岩特征点的流变位移,见表4。从量值来分析,围岩总体变形量较小,在流变计算360 d后,围岩特征点位移约为4.5~6.9 mm。从流变趋势分析,隧洞围岩各特征点流变趋势都较为一致,初期变形较大,前10 d的变形量达到2.6~4.2 mm,之后变形速率逐渐减小。流变在10~30 d进入流变衰减期,在第30 d之后变形趋于稳定,进入稳定蠕变阶段,平均变形速率为0.005~0.006 mm/d。
分析结果表明:该断面围岩变形能在30 d内趋于稳定,稳定变形速率很低,且随着流变时间的推移洞周未出现新的塑形区,因此,运行期围岩流变情况满足引水隧洞围岩长期稳定性的要求。
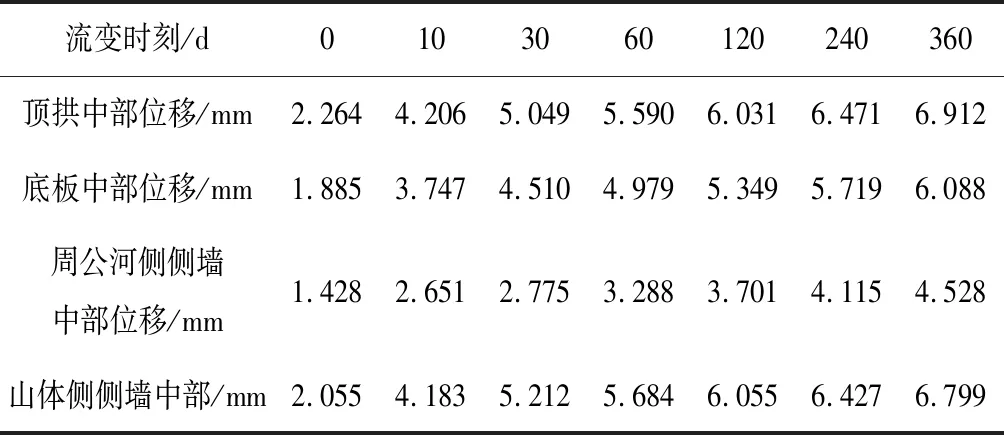
表4 不同时刻隧洞围岩特征点位移Tab.4 The characteristic point displacement of surrounding rock at different moments
表5给出了不同流变时刻洞周围岩应力最值的统计结果。从量值上分析,运行期围岩和衬砌结构主要出于受压状态,拉应力与流变时间成反比,压应力与流变时间成正比。各时刻大应力的最大压应力均出现在洞底右侧及洞顶左侧区域,洞周围岩未出现拉应力区。各时刻小主应力最大压应力均出现在围岩两侧3~4 m区域内,拉应力主要出现在衬砌结构底板右侧上,应力范围随与流变时间的推移而减小。因此,运行期围岩应力情况满足引水隧洞围岩长期稳定性的要求。

表5 流变计算过程中应力最值Tab.5 The maximum stress in the rheological calculation
6 结 语
(1)本文针对砂岩的流变特性,采用Burgers模型反映其流变变形规律。利用现有的监测资料,通过遗传算法优化BP神经网法反演得到模型中的力学参数。利用APDL编写Burgers 流变方程并接入ANSYS软件以模拟隧洞运行期稳定性分析。该预测模型能够适应隧洞充水运行条件下围岩应力状态的改变,研究成果可为引水隧洞运行期的稳定性分析提供参考。
(2)计算结果表明,该洞段引水隧洞整体稳定性良好。位移值变化较小,变形收敛速度快,稳定变形速率低;应力值趋于均匀化,应力集中程度渐少,塑性区面积较小,且进入流变稳定期后未出现新增塑性区。支护的受力情况也是安全可靠的。
□

