角点叠加法在堤防加固工程沉降量计算中的应用

张 松，叶政权，王 亮，钱 军，杨 帆

(1.扬州市勘测设计研究院有限公司，江苏 扬州 225007；2.扬州大学水利与能源动力工程学院，江苏 扬州 225127)

扬州境内长江干流长约80.4 km，江港堤防长约110 km，场地地貌分区为长江三角洲平原区。部分现状堤段的堤顶高程、顶宽、边坡等堤防断面不满足《堤防工程设计规范》(GB50286-2013)要求，须对堤身断面进行加高培厚。江堤的地基广泛分布于全新世流塑状淤泥质土，灰色稍～中密粉土、粉细砂(局部夹粉质黏土)；大部分堤段分布于深厚第2层淤泥质粉质黏土、淤泥质重粉质壤土，该层土力学强度差，对堤防的沉降稳定不利。在此类地基上对旧堤防(现状堤防)进行加高培厚设计时，需控制加固后新筑堤防的沉降量，减小新旧堤防之间的沉降差，保证加固后堤防的整体稳定性。

在《堤防工程设计规范》(GB50286-2013)中规定，可采用分层总和法计算堤身和堤基最终沉降量。在旧堤防基础上进行加高培厚后形成的新堤防，新加固的土方断面为不规则图形，应力分布具有不规则性，使得分层总和法[1]难以直接应用于加固后堤防的沉降计算。

在堤防工程设计中，本文以分层总和法的计算理论为基础，提出了角点叠加的计算方法，计算加固后堤基各部位的沉降量，得出因加固堤防而产生的沉降差，为给出合适的堤基处理工程措施及经济合理的堤基处理方案提供了理论依据。

1 堤基沉降计算方法

1.1 地基沉降

地基土的沉降计算涉及荷载作用下土中应力分布、土层的物理力学指标和计算方法等。地基土的沉降分为初始沉降、固结沉降和次固结沉降。

堤防加固设计中的沉降计算一般根据堤基的地质条件、土层的压缩性、堤身的断面尺寸和荷载分为若干段，每段选取代表性断面进行。

1.2 规范中提出的计算方法

《堤防工程设计规范》(GB50286-2013)中的堤防沉降计算方法为分层总和法，其计算公式为：

式中：S为最终沉降量，mm；n为压缩层范围内的土层数；e1i为第i土层在平均自重应力作用下的孔隙比；e2i为第i土层在平均自重应力和平均附加应力共同作用下的孔隙比；hi为第i土层的厚度，mm；m为修正系数，可取1.0，软土地基可采用1.3～1.6。

采用分层总和法进行沉降计算时，可将堤身应力简化并划分为一个矩形和两个三角形，查表分别计算其最终沉降量。

堤基压缩层的计算厚度可按堤基计算处土的附加应力与自重应力比值小于0.2控制。

2 角点叠加法计算堤防沉降步骤

2.1 角点叠加法计算堤防沉降的方法介绍

扬州市长江堤防历经数次加高培厚，显著提升了江堤的防洪能力，但现状堤顶高程、顶宽、边坡等堤防断面要素与目前的设计标准规定值仍有很大差距，故需进行加固建设。旧堤防加高培厚后，部分土方在旧堤上加高，部分土方填筑在新堤基上，除新筑堤的沉降外，旧堤因新加应力将发生新的沉降，使得堤基沉降量的计算变得较复杂。旧堤(现状堤防)加高培厚的示意如图1所示。

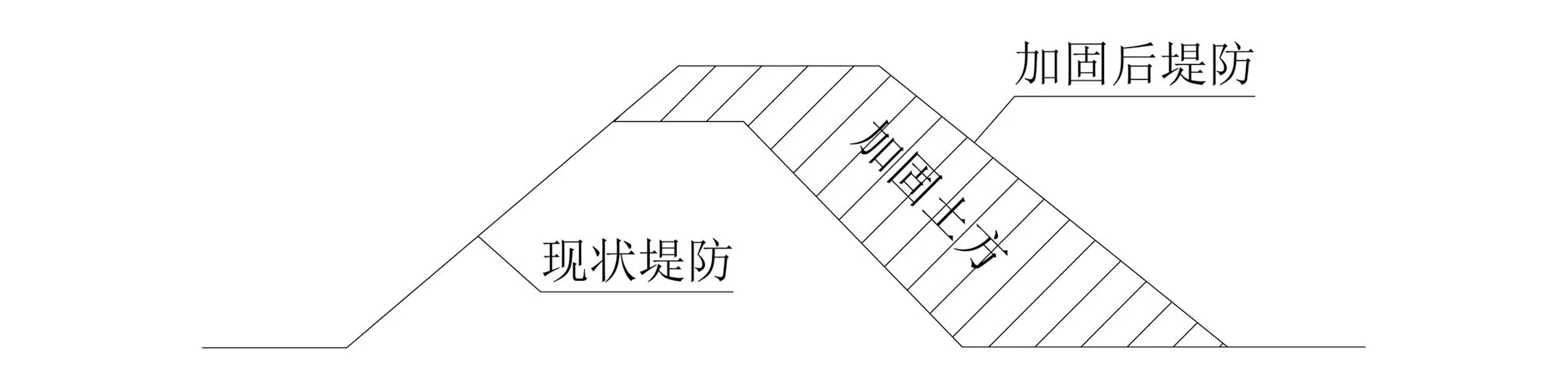
图1 加高培厚的堤防断面示意图Fig.1 Schematic diagram of the heightened and reinforced embankment

图1中堤身断面形式，因新加土方为不规则形状，将新旧堤防分格简化为多个矩形和三角形的结合体如图2，先计算由①和②两个三角形荷载产生的应力，再分别减去多算的⑥和⑦、原堤防所代表的③、④和⑤等部分荷载产生的应力，即可得出筑堤新增荷载对地基各土层产生的应力，从而计算各土层的沉降变形量，为线性显示整个堤基的不同部位的沉降量分布状况，分别对(1)、(2)、(3)、(4)、(5)、(6)和(7)等7个点(见图3)分别计算其最终沉降。以上由分块图形计算、由分布的节点表示出堤基最终沉降量的方式，命名为角点叠加法。

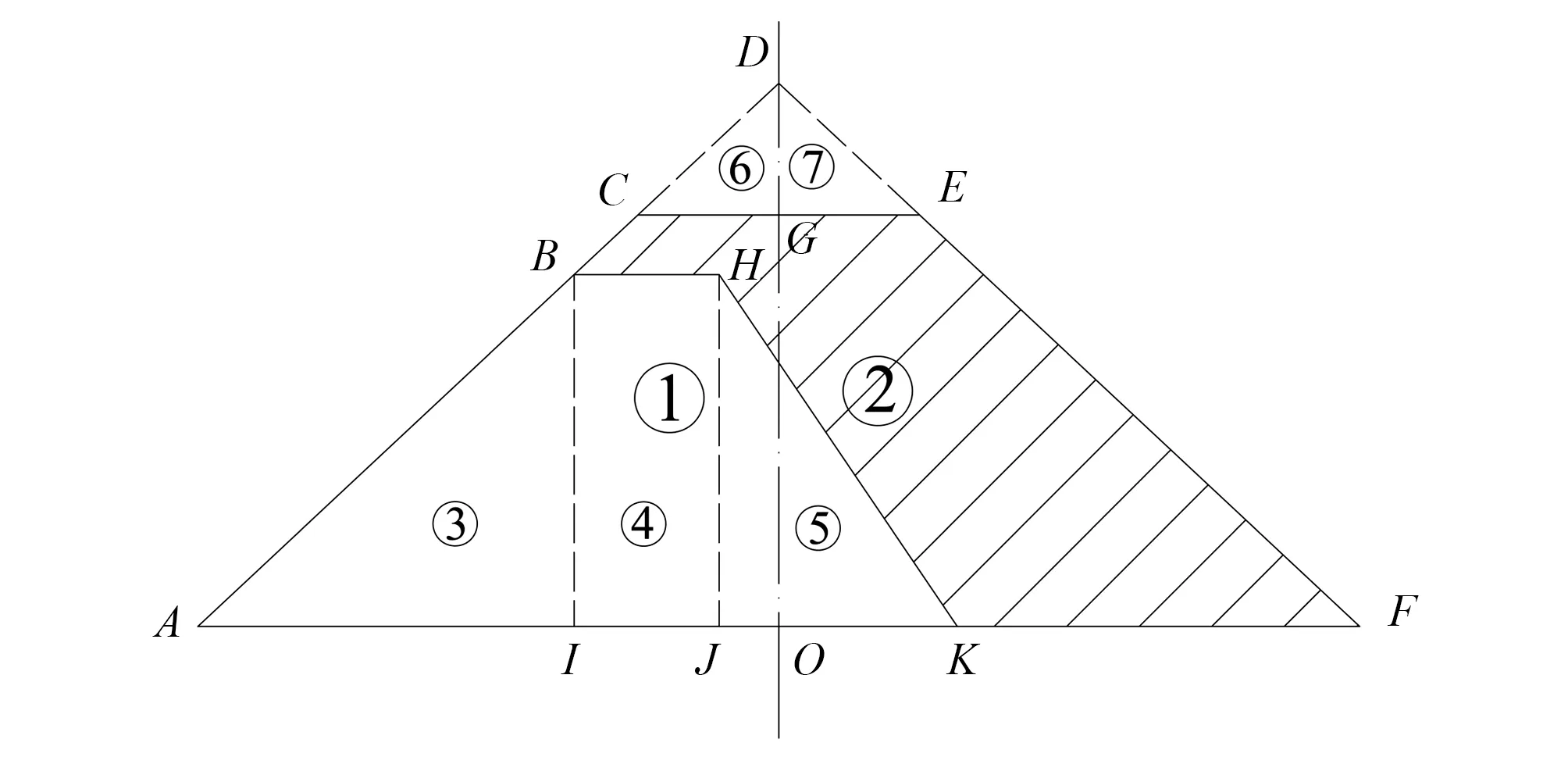
图2 角点叠加法计算示意图Fig.2 Calculation diagram of the corner addition

荷载划分荷载类型构成角点①三角形ADO②三角形DFO③三角形ABI④矩形BHJI⑤三角形HKJ⑥三角形CDG⑦三角形DEG

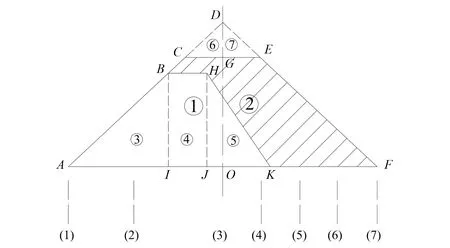
图3 点位布置示意图Fig.3 Point layout diagram

2.2 附加应力计算

如2图所示，为计算新筑堤身(即点B、C、E、F、K和H围成的区域)在地基中的附加应力，将相关载荷拼凑成①、②两个大的三角形载荷，则新筑堤身在地基中的第i层土中的竖向平均附加应力：

σzi=σ1i+σ2i+σ3i+σ4i+σ5i+σ6i+σ7i

式中：σ1i为三角形载荷①在地基中的竖向附加应力；σ2i为三角形载荷②在地基中的竖向附加应力；σ3i为三角形载荷③在地基中的竖向附加应力；σ4i为均布载荷④在地基中的竖向附加应力；σ5i为三角形载荷⑤在地基中的竖向附加应力；σ6i为三角形载荷⑥在地基中的竖向附加应力；σ7i为三角形载荷⑦在地基中的竖向附加应力。

参考文献[4]，基底均布荷载作用下的地基附加应力(图4)可按下列公式计算：

其中：m=x/b，n=z/b。

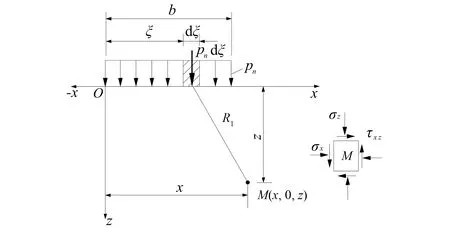
图4 基底均布形荷载作用下的地基附加应力Fig.4 Additional stress of foundation under basal uniform load

基底三角形荷载作用下的地基附加应力(图5)可按下列公式计算：

其中：m=x/b，n=z/b。

图5 基底三角形荷载作用下的地基附加应力Fig.5 Additional stress of foundation under basal triangular load

依据上述公式，可以计算各部分荷载在地基中各个点位各土层的附加应力。本次计算共选取了7个点位计算其下地基各层土的附加应力，点位布置如图3所示。

2.3 沉降量计算

地基沉降计算采用分层总和法进行计算。根据计算得到的各个点位各土层的附加应力，以及地质勘探报告个土层的压缩模量，可计算各土层在附加应力下的沉降变形量：

式中：pi为地基中第i分层平均附加应力值，kPa；Esi为地基中第i分层的压缩模量，kPa；hi为地基中第i分层的厚度，m；m为修正系数，根据《堤防工程设计规范》(GB50286-2013)[2]9.3.3可取1.0，软土地基可采用1.3～1.6；也可参考《公路路基设计规范》(JTG D30-2015)[3]7.7.2中的沉降系数计算公式进行计算，计算公式：

ms=0.123γ0.7(θH0.2+vH)+Y

式中：θ为地基处理类型系数，搅拌桩可取0.85；H为路堤中心高度；γ为填料重度，kN/m3；v为加载速率修正系数，按快速加载，速率大于70 mm/d考虑，取0.05；Y为地质因素修正系数，满足软土层不排水抗剪强度小于25 kPa、软土层厚度大于5 m、硬壳层厚度小于2.5 m三个条件时，可取0，其他情况可取-0.1。

堤基压缩层计算厚度，按下式确定：

式中：σB为计算层面处土的自重应力，kPa。

对每个点位各个土层中沉降变形量进行累加，可得到计算断面上各个点位的地基沉降量。

3 角点叠加法计算堤基沉降实例

3.1 典型断面的堤基沉降计算

扬州市长江防洪能力提升堤防加固工程中，部分堤段因堤顶高程不足，堤身较单薄，需加高加宽堤防，对于部分堤基为深20 m以上的淤泥质土的堤段，采用角点拼凑法对加高培厚后的堤防进行较精确的沉降计算，为堤基加固提供了数据支撑，保证了工程完成后堤防整体性和稳定性。

以长江堤防扬州段桩号K26+189断面为例，进行加固后的堤基沉降计算，本处堤防现状断面为：堤顶高程9.4 m，顶宽6.8 m，边坡1∶3；按规划的堤防标准，加固后的堤防断面为：堤顶高程9.7 m，顶宽8.0 m，边坡1∶3，背水坡高程7.0 m处设5 m宽青坎。加固断面如图6所示。

图6 江堤加固断面示意图(纵横比例1∶2)(单位：m)Fig.6 Schematic diagram of river embankment reinforcement

本段江堤堤基位于软土地基(2层土)上，具体地质剖面情况如图7所示。

根据地质勘测报告，2层土为黄灰、灰色淤泥质粉质黏土，此次计算所取代表断面处层厚14.2 m，含水率38.2%，压缩模量4.49 MPa，承载力80 kPa；其下卧层2-2层土为灰色轻、重粉质砂壤土，本次计算所取代表断面处层厚3.0 m，含水率32.6%，压缩模量6.65 MPa，承载力90 kPa。

采用角点拼凑法计算的堤基沉降值如表1所示。

表1 堤基沉降计算成果表 mm

图7 江堤地质剖面图(KC123孔)Fig.7 Geological section of the river embankment(hole KC123)

由于上述计算是在老堤引起的沉降已经稳定的基础上进行的，从表1可以看出：由于在堤防横断面上新加土方厚度不一，各计算点位处的附加沉降量数值很不均匀、最大沉降量达570 mm，需进行堤基处理。

3.2 典型断面的堤基处理方案比选

设计时，堤基加固方案为对沉降值较大的部位施打直径0.6 m的水泥土深层搅拌桩，桩的密度、桩长可通过采用角点叠加法计算加固后的沉降值来确定。

为了解不同布桩间距和长度的处理效果，为确定最优方案提供依据，参考《堤防工程设计规范》(GB50286-2013)、《建筑地基处理技术规范》(JGJ79-2012)等规范中有关规定，对多种不同桩基布置对堤基沉降处理的效果进行计算。计算方法如下：

搅拌桩处理后的地基沉降按复合地基变形计算方法进行计算。根据《建筑地基处理技术规范》(JGJ79-2012)7.1有关规定，复合土层压缩模量可按下式进行计算：

Esp=ζEs

式中：fak为基础底面下天然地基承载力特征值，kPa；fspk为复合地基承载力特征值，kPa；λ为单桩承载力发挥系数，可按地区经验取值；Ap为桩的截面积，m2；β为桩间土承载力发挥系数，可按地区经验取值；Ra为单桩竖向承载力特征值，kN；up为桩的周长，m；qsi为桩周第i层土的侧阻力特征值，kPa，可按地区经验确定；lpi为桩长范围内第i层土的厚度，m；ap为桩端端阻力发挥系数，应按地区经验确定；qp为桩端端阻力特征值，kPa，可按地区经验确定；对于水泥搅拌桩、旋喷桩应取未经修正的桩端地基土承载力特征值。

根据计算得到复合地基各土层压缩模量，采用角点叠加法可计算得到地基加固处理后的沉降变形情况。

计算时，桩基础间距分别取2.0、1.5和1.0 m，桩长分别取8、13和18 m(桩长18 m时已进入下卧层1.5 m)。其计算成果如表2。

采取了地基加固方案后，对减小堤基的不均匀沉降效果明显。对表2的计算成果(最大附加应力沉降)进行整理分析，汇总后如表3所示。

根据表3，绘制桩长、置换率与最终沉降量关系曲线如图8和图9所示。

根据表1、表2，绘制不同桩长、桩距处理前后各计算点沉降量变化对比图如图10所示。

4 结 语

(1)角点叠加法是基于分块图形计算、构建分布节点表示堤基最终沉降量的计算方法，该方法更便于求解加固后堤防的沉降量。经工程实际验证，角点叠加法是堤基沉降量计算较为可行的方法。

(2)根据堤基加固方案的最终实际工程反馈可知，采取地基加固对减小堤基的不均匀沉降效果明显，但无法完全避免沉降，只能在一定范围内减小沉降值。采用深搅桩加固时，加大桩的密度比增加桩长效果更好。在堤防设计时，沉降的预留值和堤基处理方案需进行多层次的计算和对比，从而采取较经济合理的设计方案。

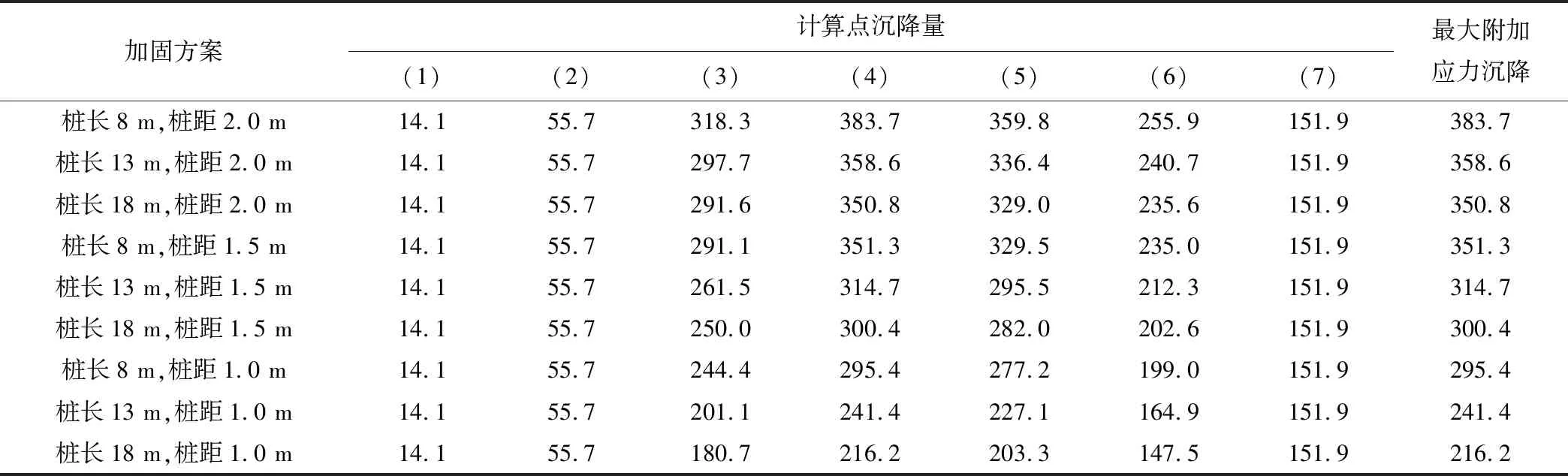
表2 加固后的各方案堤基沉降计算成果表 mm

表3 加固后的各方案堤基最大沉降量成果汇总表 mm

图8 相同置换率不同桩长沉降值变化图Fig.8 Settlement change graph at the same replacement rate

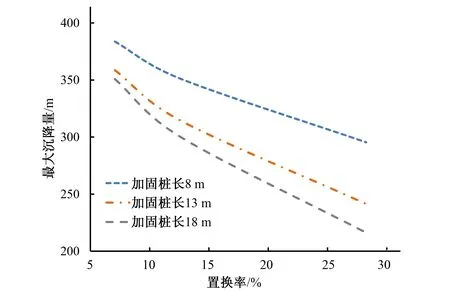
图9 相同桩长不同置换率下沉降值变化图Fig.9 Variation diagram of settlement value under the same pile length

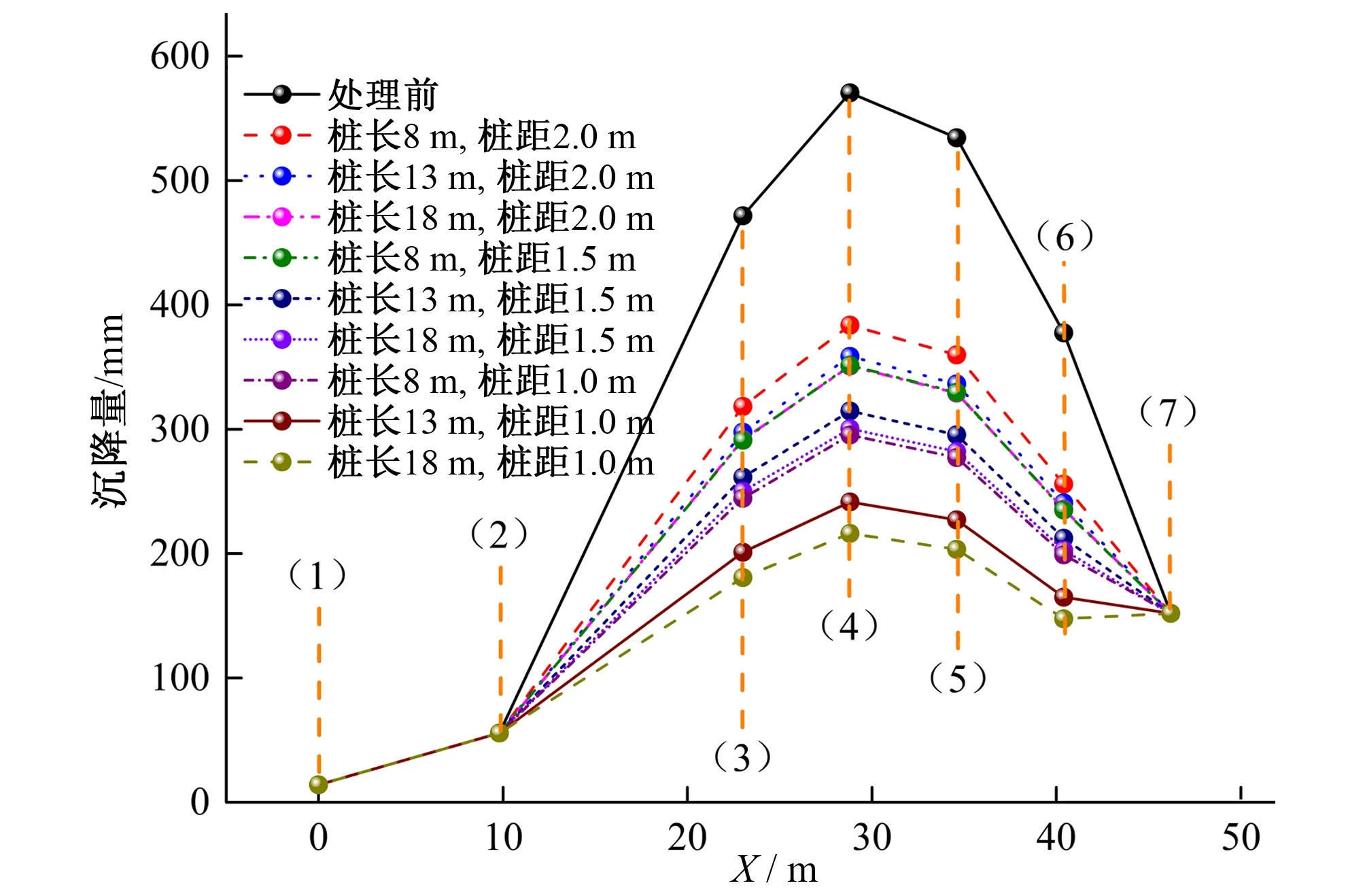
图10 不同桩长、桩距处理前后计算沉降量对比图Fig.10 Comparison of calculated settlements before and after treatment of different pile lengths and pile spacings

□