高心墙堆石坝心墙沉降变形测值延补方法研究

景玉兰，陈建康，张 瀚，牟 林，卢 祥

(1.四川大学 水力学与山区河流开发保护国家重点实验室，成都 610065；2.中国电建集团成都勘测设计研究院有限公司，成都 610072)

0 引 言

随着愈来愈多的高心墙堆石坝在我国西南地区的建设与运行，高堆石坝的心墙沉降变形特性也更加引起人们的关注[1]，掌握心墙沉降变形的原形观测资料对于避免心墙拱效应、水力劈裂及渗漏等问题[2]均有重要意义。实际工程中，因施工、水库蓄水、监测仪器或系统损坏等可能造成关键测点长期缺测或测值异常，以致无法掌握心墙沉降变形的实际规律，无法及时发现大坝出现的问题及采取补救措施。目前常用统计回归[3]、遗传回归[4]、时间序列[5]、克里金插值[6]、关联分析[7]、主成分模型树[8]等单一预测模型对堆石坝变形的缺测数据进行插补延长，或采用多种预测方法进行组合分析，其中俞凯加等[9]基于ARIMA-BP组合分析模型，考虑了监测序列的线性和非线性复合特性，钟登华等[10]基于ANFIS-GM模型，考虑了测值与影响因素的灰色特性和模糊特性，均得到了较好的预测效果。但这些模型很少能综合考虑序列的测值特性和延补期的长短，且有些方法过于复杂，对实际工程的适用性不强。本文基于高心墙堆石坝心墙沉降变形测值，比较分析了多元线性回归法、时间序列法、趋势面拟合法、克里金插值法、关联模型法等延补方法的适用性，考虑环境量、序列自身特性、空间变化规律、空间测值相关性等提出了一种适宜高心墙堆石坝心墙沉降变形测值插值延补的智适应模型。该模型能根据数据序列及延补期的长短智能而快速地计算出延补结果，能大幅提高计算效率，可为实际堆石坝工程的变形测值延补提供技术支持，也能为其他工程领域的测值延补方法提供一定参考。

1 工程背景

长河坝水电站系大渡河干流水电规划“三库22级”的第10级电站，属一等大(1)型工程。砾石土心墙堆石坝坝顶高程1 697.00 m，心墙顶高程1 696.40 m，心墙最低建基面高程1 457.00 m，最大坝高24 0 m，心墙高239.4 m。坝区河床覆盖层基本以含泥漂卵砾石等粗颗粒为主，厚度一般30～40 m。工程于2010年12月1日开工，2013年10月30日开始下游堆石区填筑，2016年9月17日竣工，2016年10月25日开始蓄水，2017年12月7日初蓄完成。

长河坝沉降变形监测主要采用电位器式位移计、电磁式沉降仪、水管式沉降仪。其中心墙填筑区埋设36套电位器式位移计，分布于0+193、0+253、0+330三个监测断面，编号WY14～17、WY19～24、WY26～29、WY31～34、WY36～41、WY43～46、WY48～51、WY53～56，如图1所示；心墙填筑区埋设3套55个电磁沉降环，分布于0+137、0+253、0+394三个监测断面，编号VE1-DC1～ DC15、VE2-DC1～ DC23、VE3-DC1～ DC17，如图2所示；下游堆石区埋设124个水管式沉降仪，分布于0+137、0+193、0+253、0+330、0+394五个监测断面，编号CH1～ CH124，图1所示水管式沉降仪有CH41～CH55、CH57～CH61、CH65～CH69。

长河坝大坝填筑施工中， VE1～VE3仪器下部的沉降环因挤压变形过大而无法测值，多数测环无法获取2015年9月至2016年7月的测值，致使无法判断是否捕捉到该时段心墙的最大沉降变形，应工程蓄水安全鉴定需求，需对异常及缺测测点进行测值延补以掌握大坝的实际运行性态。

图1 心墙区0+253断面电位器式位移计监测布置图(单位：mm)Fig.1 Monitoring layout of Potentiometer displacement meters in 0+253 m section

图2 沿心墙中心线断面电磁式沉降环监测布置图Fig.2 Monitoring layout of electromagnetic settlement rings of the section along the center line of the core wall

2 高心墙堆石坝心墙沉降变形测值延补智适应模型研究

2.1 传统常用延补方法

2.1.1 时间延补法

(1)多元线性回归法。多元线性回归法是一种以环境量作为自变量，监测效应量为因变量，基于数理统计建立起的数学模型。考虑以下延补时段为心墙填筑期，可建立如下回归模型：

(1)

式中：y(t)为心墙沉降变形监测值在时间t的统计估计值；H(t)为t时刻心墙上升高度；T(t)为从起始监测日算起至当前观测日的累积天数除以100；ai(i=1，2，3，4)为待定回归系数。

(2)时间序列法。大坝监测数据时间序列法可在不涉及环境量的条件下，根据测值时间序列的规律性、不变性及数据间的非独立性构建如下时序模型：

xt=f(xt-1,xt-2,…,x1)+at

(2)

式中：{xt}为大坝变形实测值的时间序列；f为当前测值与历史测值的相关关系；at为随机因素，通常假定为白噪声序列，令其均值为0。经计算，该心墙堆石坝沉降变形序列基本呈自相关系数拖尾，偏自相关系数一阶截尾，因此考虑测值序列符合AR(P)模型。

2.1.2 空间延补法

(1)趋势面拟合法。在外界荷载及环境等因素的作用下，坝体任意一点的变形都与空间坐标存在相关关系[11]，趋势面拟合法正是对多个测点、多个方向的测值进行综合分析的方法，构建趋势面函数如下：

(3)

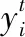
(4)

式中：λi为待定权重系数，可通过实验变异函数与变异函数模型拟合得出，此处采用的变异函数模型为球状模型。

(3)关联模型法。大坝沉降变形一般有若干个监测断面，各断面沿高程或上下游方向均会布置一系列测点，由于各断面外部环境、荷载条件和仪器基本一致，因此同一断面相邻测点的沉降变形测值及其变化趋势一般具有很强的相关性。对于关联度较大的测点，可根据测点测值直接建立关联模型，序列之间的关联强度可通过相关系数的大小来判别，如表1所示。

表1 相关系数和相关强度关系Tab.1 The relationship between correlation coefficient and correlation strength

2.2 延补效果分析

对于时间延补法，取长河坝工程心墙部位WY33、WY40和VE2-DC11、VE3-DC8作为验证测点，分不同时段分别对其进行多元线性回归和时间序列建模。由表2可知，两种方法均适用于短期延补。由于要建立效应量与多个自变量的数理关系，多元线性回归法较适用于长序列数据；建模时采用的因子及表达式受人为主控因素的影响较大，可能造成因子的漏取和误取，加之受随机因素的影响，模型的延补精度会随着时间的增加而逐渐降低，该法在120 d以内的延补精度较高，最大相对误差M(ΔA(%))基本可控制在17%以内，复相关系数R均大于0.9。时间序列法要求序列为自相关程度较高的等时间间隔连续数据，对如图3所示测点VE2-DC11、VE3-DC8的非等间距、非平稳序列不适用；建模时主要依靠数据内部的依存关系来预测数据的发展趋势，更适用于短序列的短期延补，该法在15 d以内的延补精度较高，且略高于多元线性回归法，复相关系数R均大于0.8，但随着延补时间的增加，延补值几乎处于不变或缓慢增长的状态，属无效值。

对于空间延补法，取长河坝工程心墙部位的电磁式沉降环VE1-DC5～VE1-DC8、VE2-DC10～ VE2-DC13作为验证测点，取下游堆石区同监测断面相近高程的水管式沉降仪作为参照测点。由表3可知，由于三种方法均无时间维度，仅受基础测点个数、相关程度及空间位置的影响，误差不随时间波动，对序列的短期和长期延补均适用。关联模型法的延补精度最高，延补测点与参照测点间的相关系数均大于0.87，从平均误差来看稳定性较好，但其受限于参照点的个数及其与延补测点间的相

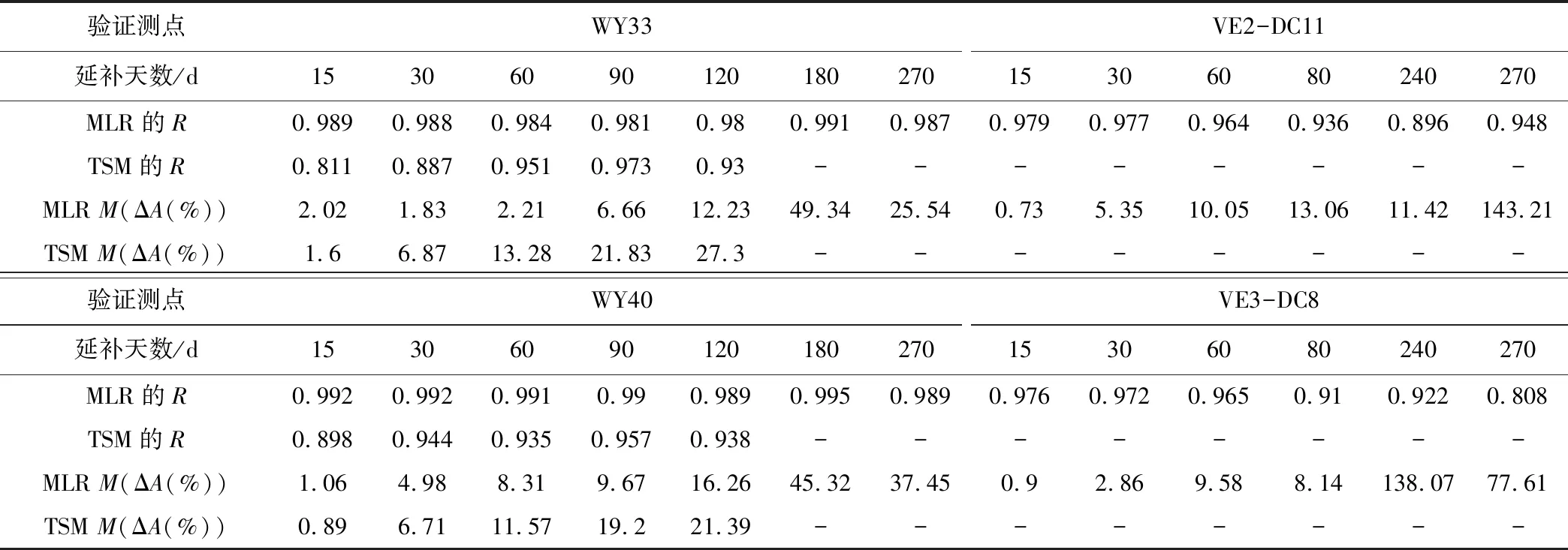
表2 典型测点沉降变形多元线性回归法与时间序列法延补精度对比Tab.2 Comparison between MLR and TSM of settlement deformation of typical measuring points

图3 测点VE2-DC11、VE3-DC8沉降变形多元线性回归法不同时段延补历时过程线Fig.3 MLR for settlement deformation in VE2-DC11 and VE3-DC8

表3 典型测点沉降变形空间延补法精度对比Tab.3 Precision comparison of space interpolation and extension method for settlement deformation of typical measuring points

关程度，参照点越多且相关度越高，测值延补误差越小。从平均误差来看，趋势面拟合法与克里金插值法的延补精度相当。由于在此建立的是一次三元趋势面方程，趋势面拟合对于变化复杂的插值情形适用效果不佳，拟合表面较少地通过原观测点，导致各测点的延补误差较大；虽然克里金插值的延补精度较高，但半变异函数受人为选定影响较大，且插值曲面通常比真实曲面平滑，导致个别测点的延补测值出现极值，稳定性相对较差。

2.3 智适应模型的构建与应用

2.3.1 智适应模型构建

高心墙堆石坝一般位于高山峡谷地区，坝区环境条件复杂，影响坝体各部分变形的因素众多，而传统常用的单一时间延补法和空间延补法在心墙沉降变形延补过程中不能综合考虑环境变量、序列自身特性、空间变化规律和空间测值相关性的影响。因此基于高心墙堆石坝心墙沉降变形特征，结合传统方法的延补精度、适用性及其计算的复杂程度，构建了适宜高心墙堆石坝心墙沉降变形测值的智能适应模型，该模型可根据各测点的测值特性从优选择延补方法，以求得到较高的延补精度，具体流程见图4。多元线性回归和时间序列的短期延补精度较高，短序列15 d以内的延补宜优先选用时间序列法，长序列120 d以内的延补宜优先选用多元线性回归法。三种空间延补法对长、短序列的延补均适用，综合考虑表1及表3，可认为当延补测点与参照测点间的相关系数≥0.8时，两者呈极强相关性，且此时延补精度较高。当短序列的延补期超过15 d或长序列的延补期超过120 d时，宜优先选用关联模型法；若参照序列的相关度小于0.8，宜改用趋势面拟合法和克里金插值法，对两种方法计算得出的相对误差进行比较，选取误差较小的方法。为验证智适应模型的延补精度，取长河坝心墙区WY33作为验证测点，与上述单一的多元线性回归延补结果相对比，见表4。可知，智适应模型的延补精度明显高于传统方法，且该测点270 d以内测值延补的相对误差均可控制在10%以内。

图4 高心墙堆石坝心墙沉降变形测值延补智适应模型Fig.4 Intelligence adaptation model for settlement deformation of core wall of high core rockfill dam

表4 测点WY33智适应模型与传统方法延补精度对比Tab.4 Precision comparison of intelligence adaptation model and traditional method in WY33

2.3.2 应用效果分析

将上述智适应模型应用于长河坝2015年9月至2016年7月心墙区电磁沉降环VE1-DC3～ DC8、VE2-DC6～ DC13、VE3-DC2～ DC10的测值延补中，其中四个典型日期沿心墙中心线断面的沉降变形分布见图5。可看出，不同时段延补后的长河坝心墙沉降变形均呈现出沿高程方向中部大、顶部和底部小，沿坝轴线方向河床中部大、两岸岸坡小的分布特征，左右岸岸坡沉降较为接近，符合高心墙堆石坝心墙沉降变形的一般规律。结合原观监测资料分析，截止2016年7月30日，心墙最大沉降量为1 950 mm，发生在(纵)0+253.00断面1 590.50 m高程测点处的电磁沉降环VE2-DC12。经插补延长，截止2016年7月30日，心墙最大沉降值仍位于测环VE2-DC12处，量值为1 985.23 mm，仅与延补前相差35.23 mm，占心墙最大填筑高度229 m的0.87%，且与类似工程瀑布沟水电站填筑期的沉降变形特征相似，见表5。

图5 沿心墙中心线断面不同时段沉降分布图Fig.5 Settlement distribution at different periods along the central section of core wall

3 结 语

(1)通过对常用数据延补方法的精度分析可看出，多元线性回归法适用于长序列120 d以内的短期延补；时间序列法更适用于短序列15 d以内的超短期延补，且其15 d以内的延补精度略高于多元线性回归法。当延补序列与参照序列呈极强相关性时，关联模型法的延补精度较高，且高于克里金插值法和趋势面法，后两者的精度相当，三种方法对长、短序列的短期和长期延补均适用。

(2)鉴于传统常用的数据延补方法各有其优缺点和适用性，基于高心墙堆石坝心墙沉降变形测值，考虑环境量、序列自身特性、空间变化规律、空间测值相关性等，提出了一种适宜高心墙堆石坝心墙沉降变形测值插值延补的智适应模型。

(3)高心墙堆石坝心墙沉降变形测值延补智适应模型在长河坝心墙沉降变形测值延补的应用表明，延补结果符合心墙沉降时变趋势，心墙最大沉降变形占心墙填筑高度比与瀑布沟工程具有相似性，验证了模型的合理性与有效性，具有良好的工程应用价值。

□