不同洪量对洪家渡水库水温分层结构影响分析

张 鹏 飞

(黄河水利职业技术学院，郑州 475004)

0 引 言

水温是评价深水水库水环境重要因子之一[1]，在水库水生态系统变化过程中起着重要作用。对于深水型水库，下层水体常年水温较低，上层水体由于受到外界因素的影响相对而言温度较高，因此会出现垂向分层的现象，水库水温的分层结构一定程度上代表库区内水体热量的空间分布特征[2]。影响水库水温分层的因素[3-5]有水文因素、进出水口位置、调度方案、地形条件、库内水深等因素，根据这些因子的影响强弱，库区内水温结构由强到弱可划分为：分层型、过渡型和混合型[6]。一般而言，一年内分层型水库水温结构会出现周期性的变化[7]，在表温层，由于有空气对流和风浪等作用，表层水体快速混合，水温变化不大，表温层的深度主要取决于水体的稳定性及水动力条件[8,9]；表温层以下水体会产生温度突变，称为温跃层；温跃层以下水体温度较低，库底热量变化平稳，称为滞温层[10-12]。库区内水体水温分层加剧了水环境的变化，对水质、水生生物的繁衍、新陈代谢、群落结构及分布有着重要影响[13]，在不同的洪量下分层结构又会发生变化，因此研究不同洪量下水库水温分层结构有着重要意义。

目前研究水库水温变化主要有经验法和数值模拟法[14]，相比经验法，数值模拟法因考虑了热交换、气候条件、水动力等因素[15]能较好地用于探讨水温变化规律而得到广泛应用。目前针对水温模拟的一维、二维、三维数值软件非常成熟，相比二维模型，三维模型能较好地处理研究区地形情况、水流运动特性、边界情况等问题而被广泛应用于湖、库水环境研究中，龙圣海[16]等利用MIKE 3较好的预测了金盆水库水温全年水温变化过程，刘晋高[17]等通过CE-QUAL-W2分析三峡水库不同异重流条件下水体的水温分布情况，赵一慧[18]等通过EFDC较好的预测小浪底水库的坝前水温分布。

近年来随着水资源开发利用程度的加大，梯级水电站越来越多，随着梯级水库的建立，天然河流的水流情势、库区水体热量分配会发生变化，相应河段水体的水温也随之改变[19-21]。目前研究水库水体温度分层的文章较多，但有关在不同洪量下水库水温分层情况的报道却极少，尤其是对于梯级电站，又因EFDC模型拥有能灵活的边界处理技术，能快速的耦合水动力、泥沙和水质模块，能较好拟合近岸复杂的岸线和地形等优点，故本研究建立了洪家渡水库的EFDC水温模型，拟对洪水历时进行考虑，以3 d洪水、5 d洪水、7 d洪水进行研究，针对不同的历时结合EFDC模型计算分析不同洪量对洪家渡水库水温分层结构的影响。

1 洪家渡水库水动力模型建立

1.1 研究区域概况

洪家渡水电站(26°51′ ～27°02′N， 105°32′～105°55′E)位于贵州省毕节市黔西县与织金县交界的乌江干流北源六冲河下游段，是乌江干流梯级开发的第3级电站，洪家渡水库不承担下游防洪任务，工程规模为一等，为多年调节水库，电站装机容量60 万kW(3×20)，年均发电量15.94 亿kWH。水库正常蓄水位1 140 m，库容49.47 亿m3，调节库容33.61 亿m3。

1.2 模型简介

EFDC模型是美国环保署支持的三维环境流体动力学数值模型，被广泛用于模拟水系统一维、二维和三维流场、物质输运(包括温度、盐度和泥沙的输运)、生态过程以及淡水入流等。目前，该模型还增强了很多水动力过程模拟因素，包括植被阻力、干度和湿度、水动力结构的表示、波浪和湖流边界层的相互作用以及波动流等。该模型拥有完整的前、后处理软件，采用可视化的界面操作，能快速的生成网格数据和处理图像文件，计算效率较高，运行速率大约是 POM 的1.85倍。随着EFDC模型的不断发展，其功能愈加完善和强大，应用越来越广泛。

EFDC模型通过控制方程物理量，通过二阶空间有限差分格式求解，采用三层有限差分格式作为模型的时间积分分解求出，通过隐式差分、显式差分分别计算垂向扩散项、水平扩散项，水平方向上采用平面正交模型进行转换、垂直方向上采用sigma坐标进行转换，对于不规则区域，一般先转化再进行网格剖分。坐标转换方程如下：

x=x(x*,y*)

y=y(x*,y*)

z=(z*+h)/(ε+h)

(1)

式中：x*、y*、z*分别表示横向、纵向、垂向坐标；x、y、z分别为按对应的坐标系转换后的横向、纵向、垂向坐标；ε表示垂向坐标；h为底部地形高程。

2.4 两组围生儿并发症发生情况 羊水过少组围生儿共77胎，正常组围生儿共78胎。羊水过少组新生儿窒息、足月低体质量儿、胎儿宫内窘迫、吸入性肺炎等围生期并发症发生率均明显高于正常组，差异均有统计学意义(P<0.05)。见表4。

模型经过上述坐标转换后对应的连续方程、动量方程、温度输运方程分别如下：

(2)

(3)

(4)

式中：mx、my是坐标转换系数(其中m=mxmy)；u、v是转换后坐标系下x、y方向上的速度分量。

热输运方程公式为：

(5)

I=rIsexp[-βfH(1-z)]+(1-r)Isexp[-βsH(1-z)]

(6)

式中：I为太阳短波辐射率；βf为快尺度的衰减系数；βs为慢尺度下的衰减系数；r为分配系数(值为0～1)。

1.3 模型的离散求解

采用二阶精度的空间有限差分格式求解控制方程，变量布置采用交错网格。模型的时间积分采用具有二阶精度的三层有限差分格式，采用内外模分裂方式将物理过程分解为内模(斜压模态)和外模(正压模态)。外模求解采用半隐格式，利用预处理共轭梯度法同时求解二维水位场。以新的水位值为基础，通过求解水深平均的正压速度场得到外模解。外模求解的水平边界条件包括如下选项：给定表面水位、入流特性、自由辐射的出流条件、边界的任意部分给定法向体积流量。在和外模相同的时间步内，内模求解垂向扩散项采用隐格式。动量方程内模主要是求解应力和速度的垂向分布。三层时间格式中的时间分裂由周期性插入一个二阶精度的两层时间格式完成。

1.4 网格的构建

洪家渡坝址处河谷断面为不对称“V”形，左岸陡峭，为70°～80°的灰岩陡壁。右岸相对较缓，为35°～45°的坡地。概化出的洪家渡水电站河底地形见图1，网格边长为25 m，共划分得7 824个网格，垂向分为40层。

1.5 初始条件的确定

1.5.1 初始水位

1.5.2 初始水温条件

根据2013年洪家渡水库坝前断面实测资料情况，洪家渡水库2～15 m为温跃层，温差达到5.2 ℃，洪家渡水库水温分层区域为整个库区。依据温跃层分布情况，将水库水深沿垂向由小到大分为20层。初始水温分布根据2013年洪家渡水库坝前实测垂向分布水温设定，取值为模拟月份前一个月的水温垂向分布值，没有给定的水层初始水温按相邻两层的数值进行线性内插。采用2013年洪家渡水库上游实测水温作为主流入库断面水温，2013年洪家渡水库坝前实测垂向分布水温见表2。

图1 洪家渡水电站河底地形图

表1 2013年洪家渡水库各月平均水位 m

表2 2013年洪家渡水库坝前断面各月垂向水温分布表 ℃

1.5.3 边界条件

(1)流量边界条件。共设3个开边界，凹水河和入库水流(白甫河和木白河)汇合后于出库断面流出。主流入库流量为总入库流量减去同时刻的支流流量；洪家渡库区主要的支流有三条，凹水河、木白河和白甫河，由于能获取的支流流量的数据不足，能获取的支流对应的年平均流量分别为7.9、6.45、30.6 m3/s；丰水期流量分别为11.06、9.03、42.84 m3/s；枯水期流量分别为4.74、3.87、18.36 m3/s。根据研究区域水文特性，将6-9月划分为丰水期，12、1、2月划分为枯水期，其他月份为平水期，模型计算时平水期入库流量采用对应河段的年均流量，为保证月均水位相等，因此出库流量设定值与入库流量相同，出库流量等于各河段入库流量之和，最后将对应边界的入库、出库流量平均分配到每一层中。

(2)水位边界。洪家渡水库出库流量考虑模型计算的稳定性，按月均水位给定下游水动力边界条件。

(3)水温边界条件的确定。入流水温边界分为两种，一种是主流的入库水温，另一种为支流凹水河的入库水温。由于支流凹水河是天然河道，水深较浅，河道特征明显，垂向断面水温混合均匀，故采用相应月份的天然水温作为凹水河入库水温，而主流的水温由于受上游引子渡水电站下泄水温的影响故不能采用天然水温，应采用2013年洪家渡坝前断面实测值(见表2)。 出流水温根据2013年洪家渡水库下泄水温实测值给定，具体实测值见表3。

表3 2013年洪家渡水库下泄水温实测值 ℃

注：表中数据为各月水温的平均值。

(4)大气边界条件。大气边界条件中大气压、空气温度、空气湿度、降雨量根据当地实测资料给定，蒸发量、太阳辐射量及云量利用模型，根据给定的实测大气边界条件及洪家渡水电站经纬度自行运算。

1.6 模型率定验证

根据模型各参数之间的影响规律，采用试算法进行率定计算，即先根据经验(或模型中的默认值)给出参数初始取值，再对模拟值和实际值进行比较，反复调整和试算，直到模拟结果与实测结果拟合效果较好为止，根据2013年洪家渡水库坝前断面各月垂向水温进行模型的率定验证，坝前断面各率定月份模型模拟出的水温垂向分布曲线和实测值对比分别见图2～图5。

图2 2013年4月洪家渡坝前垂向水温分布

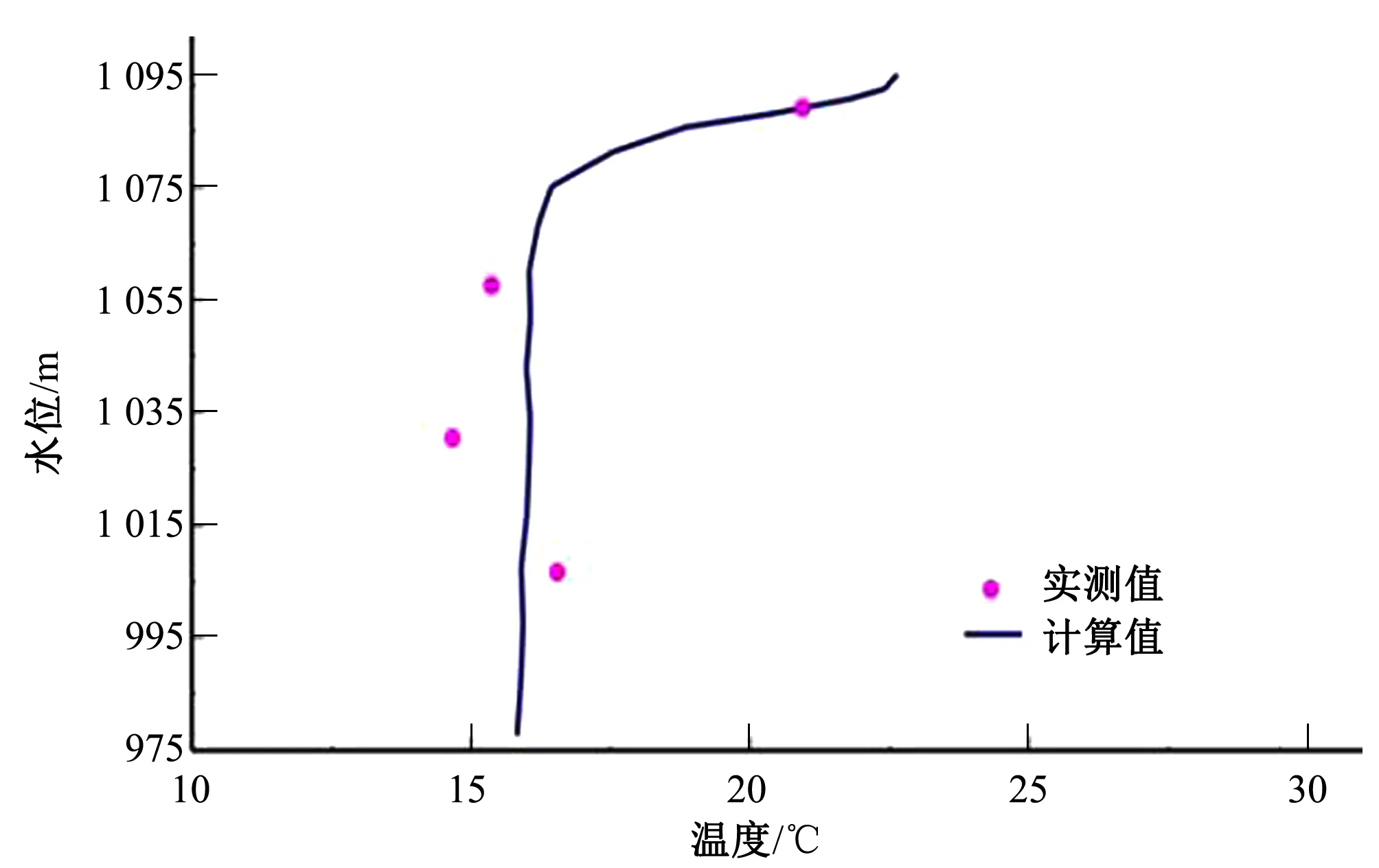
图4 2013年10月洪家渡坝前垂向水温分布

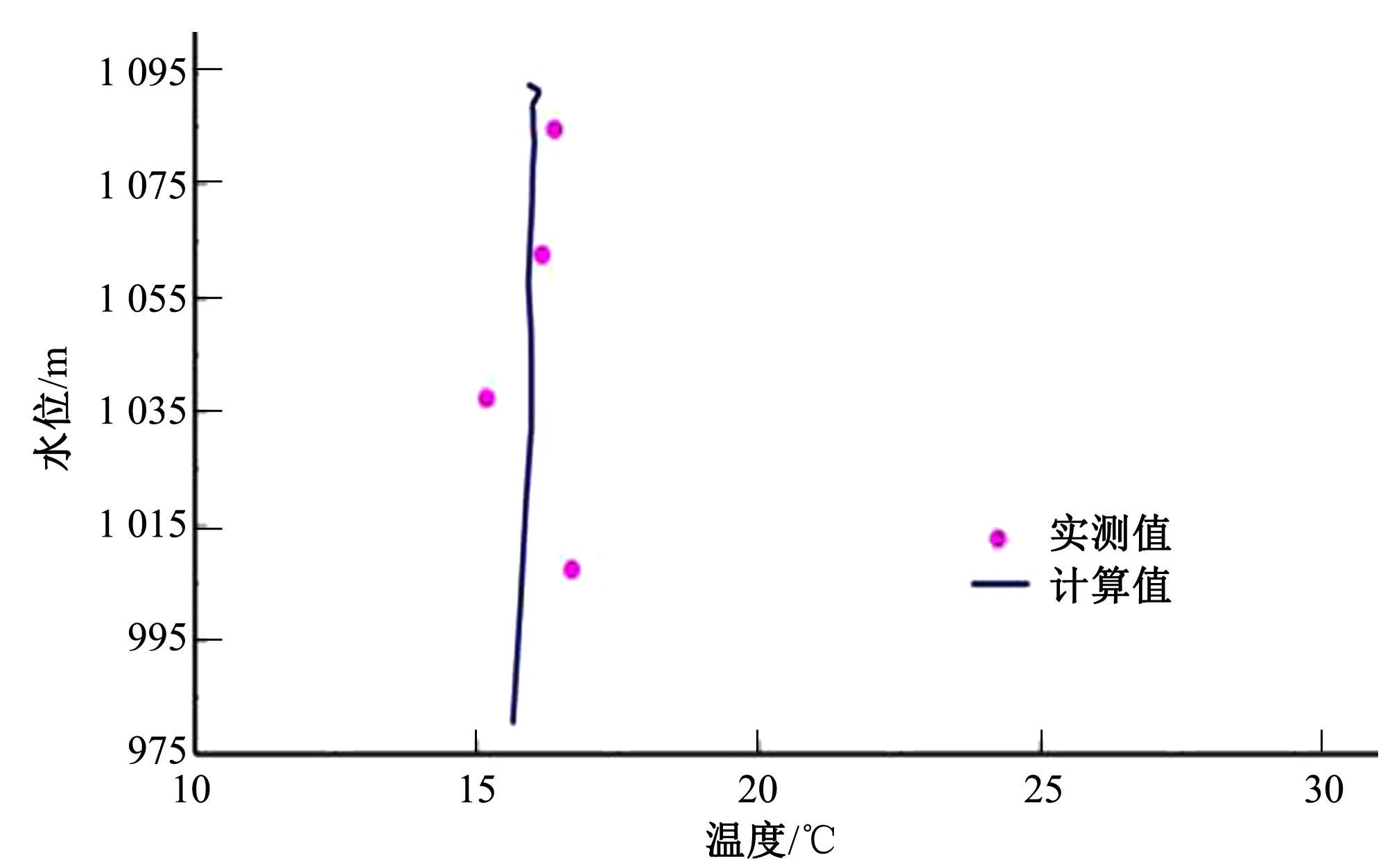
图5 2013年12月洪家渡坝前垂向水温分布

从上图率定结果表明：①洪家渡水库水温结构为分层型，与经验法结论一致；②7月、10月库区坝前水温出现分层现象，水温随深度的增加而逐渐降低，上层水体水温变幅较大，下层水体水温变幅较小，尤其7月份，库区上下层水体水温温差达到10 ℃；③库区坝前水温在4月、12月上下层水体水温相差不大(温差在2 ℃以内)，笔者推测11月以后由于气温的降低，表层水体水温随着降低，上层水体与下层水体产生对流现象，上下层水体发生翻转致使水温趋于一致；④模型水温计算值与实际水温监测值差值在0.5～2.7 ℃，模型率定效果较好，可以用来模拟与计算洪家渡库区的水温分布情况。

根据对洪家渡水电站水温的率定，得到EFDC模型计算水温率定的参数如下：蒸发传热系数 1.5、净水消光系数 0.45、总悬浮固体消光系数 0、水体表层水最小太阳辐射吸收率 0.45、河床热力厚度13 m、初始河床温度12 ℃、河床反射到水体的太阳辐射的比率 0.003、河床和水体之间的传热系数 0.3。

2 不同洪量对水库水温分层结构影响

目前径流-库容比法(α-β法)是判别水库水温结构常用的经验公式法[8]。其中α值为多年平均流量与水库总库容的比值，当α<10时为稳定分层型，10≤α≤20 时为不稳定分层型，α> 20 时为混合型；其中β参数表征了汛期洪水对水温分层结构影响程度，其值为一次洪水量与水库库容的比值，当β>1时，洪水对水温结构有影响，为临时混合型；当β<0.5时，洪水对水温结构无影响；当0.5<β<1，洪水对水温结构有一定影响，但未破坏水温的分层结构。这个经验公式的一次洪水量未明确洪水的具体历时，当一次洪水量相同但历时不同时，对水库水温分层结构的影响也不一样，根据上文α计算方法判断得本水库α<10，故为稳定分层型。为了具体分析研究不同历时的一次洪水量对水库水温分层结构的影响，取洪家渡水库库容V=45 亿m3做模型计算，选取3 d洪量、5 d洪量、7 d洪量来计算一次洪水量水库水温分层结构所造成的影响，这种影响以库表与水库深度为5、20、40、80 m的温差来体现，当一次洪水量相同但历时不同时，库表与水库各深度的温差值也不相同，通过模型的计算来说明温差的具体差异。

模型计算时，根据设置的流量边界对水库分别计算出3 d洪量、5 d洪量、7 d洪量对水库水温分层结构的影响，计算结果见图6。

由图6分析知：洪水量越大，洪水对水温的分层结构影响越小，即库表与各深度的温差越大。当一次洪水量相同时，历时越长，洪水对水温的分层结构影响越小，即库表与各深度的温差越大。

根据模型计算结果，得到3 d洪量、5 d洪量、7 d洪量情况

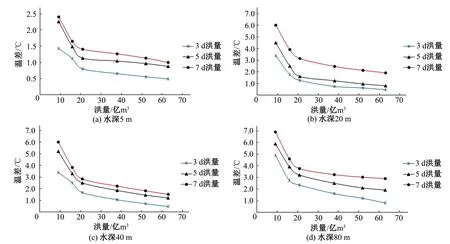
图6 不同洪量下水库库表与各深度(5、20、40、80 m)水体温度的差值

下水库水体在不同β值下库表与各深度水体的温差值，结果见表4。

表4 不同洪量、不同β值下水库库表与各深度的温差值 ℃

从表4知：在3 d洪量条件下，当β=0.15时，库表与库底的温差为4.50 ℃；当β=1.9时库表与库底的温差为0.60 ℃；当β从0.15～1.95变化时，库表与库底温差为3.90 ℃。

在5 d洪量条件下，当β=0.15时，库表与库底的温差为5.21 ℃；当β=1.95时，库表与库底的温差为0.57 ℃；当β从0.15～1.95变化时，库表与库底温差为4.64 ℃。

在7 d洪量条件下，当β=0.15时，库表与库底的温差为6.32 ℃，当β=1.95时，库表与库底的温差为0.81 ℃。当β从0.15～1.95变化时，温差为5.51 ℃。

分析可知：当一次洪水量相同且历时相同时，β值越大，水库混合程度越好，即库表与库底的温差越小；当一次洪水量相同且β值相同时，历时越长，库表与各深度的温差越大。

3 结 语

本文选取梯级水电站中的其中一个水库为研究对象，通过建立EFDC三维水温模型，采用2013年实测水温数据对模型进行率定，用2014年实测水温数据进行验证，模拟并分析了全年典型月份洪家渡水库水温分层结构特征，在此基础上进一步探讨了不同洪量下对库区水温分层结构的影响，研究表明。

(1)EFDC水温模型由于充分考虑了热交换、出入库流量、风向、风速、降雨、气温等因素，模拟值与实测值吻合度较高，说明EFDC模型结构合理、模拟结果可靠，可广泛应用于深水型水库水温预测中；

(2)洪家渡水库水温结构为明显分层型，在7-10月分层较为明显，上下层水体温差可达10 ℃，12-4月份上下层水温相差不大；

(3)一次洪水量相同且历时相同时，β值(一次洪水量与水库库容的比值)越大，水库混合程度越好，即库表与库底的温差越小；当一次洪水量相同且β值相同时，历时越长，库表与各深度的温差越大。

□