基于地形地貌参数确定地貌单位线中的平均流速

董丰成，石 朋,2，纪小敏，赵兰兰，陈颖冰，瞿思敏，崔彦萍

(1.河海大学水文水资源学院，南京 210098；2.河海大学水文水资源与水利工程科学国家重点实验室，南京 210098； 3.江苏省水文水资源勘测局，南京 210029；4.水利部信息中心，北京 100053)

流域水文响应是地貌扩散和水动力扩散对降落在流域上具有一定时空分布的净雨共同作用的结果。一直以来，水文学家和地理学家尝试着研究这种汇流机理以建立地形地貌特征和流域水文响应之间的关系，从而为无资料或资料匮乏区的汇流计算提供了一种解决办法。最早在这个方向取得突破性研究成果的是RODRGUEZ[1]、VALDES[2]等人关于地貌瞬时单位线(GIUH)理论的建立和应用。自此之后，越来越多的学者开始了对GIUH的关注和研究。芮孝芳[3]等通过分析流域水文响应机理提出了基于地貌扩散和水动力扩散的GIUH，石朋[4,5]等创建了由自相似网格构建GIUH并提出了考虑水流空间变异性的GIUH，邹霞[6]等应对现有GIUH对坡面汇流考虑的不足，提出了考虑坡面汇流的改进GIUH模型。

由于其不依赖于历史水雨情资料的特点，GIUH对于解决无资料或资料匮乏区的汇流计算问题具有显著优势。芮孝芳等[7]揭示了GIUH的实质是描述流域面上分布均匀的雨滴持留时间的概率密度函数。因此，水滴的汇流速度就成为计算地貌瞬时单位线的一个重要因子。在已有的关于GIUH的研究中，针对其汇流速度确定方法的研究并不多见。KUMAR[8]等建立流域平均流速与最大雨强以及河道断面、实测洪水信息之间的经验关系，NONGTHOMBAM[9]提出了一个与坡长及坡度有关的流速计算经验公式，并将此方法应用到印度的一个小流域进行洪水模拟。本文拟从统计角度出发，通过对多个源头型中小自然流域的分析，建立流域平均汇流速度同地形地貌因子之间的函数关系，并将此关系在其他流域进行应用检验，以探讨这种确定流速方法的适用性。

1 流域平均流速与地形地貌因子的相关关系

1.1 流域最优表征的平均流速

地貌瞬时单位线方法能否有效地应用于无水文资料地区，关键在于是否能够求得合适的流域平均汇流速度。然而，水文学发展到今天，还没有合适的科学方法测定流域实际的平均流速数值。本文通过率定优选的方式获取流域最优表征的平均流速，以此代表流域的实际平均流速，其中，流域最优表征的平均流速是指，当应用地貌瞬时单位线方法对流域上分布一定的净雨进行汇流计算时，使得计算与实际的汇流过程拟合程度最优时的平均流速。在率定优选时，为了使目标函数能够全面地描述由实测资料所反映的水文特征，根据GB/T 22482-2008《水文情报预报规范》中的精度评定指标，在计算场次洪水时，选用以径流深相对误差(RRe)、洪峰相对误差(RPE)、峰现时差(RTE)和确定性系数(DC)四个指标建立的综合误差系数(CEC)[10]作为目标函数，即：

CEC=(RRE+RPE+RTE+DC)/4

CEC介于0～1之间，CEC值越大，表明模型计算结果越好。

首先，利用新安江模型，对实测的历史场次洪水进行模拟计算，优选出模型参数，其中模型中的地表径流是通过线性水库的方法演算到流域出口。然后，在不改变新安江模型其他计算模块的前提下，调整地表径流的汇流方式，将地表径流直接汇入河网，形成河网的总入流；再将河网的总入流通过地貌瞬时单位线演算至流域出口，从而建立流域的地貌瞬时单位线模型。最后，地貌瞬时单位线模型直接移用新安江模型中相对应的最优参数值，并仍以综合误差系数作为目标函数，通过率定优选确定使得目标函数值最优时的平均流速数值，即流域最优表征的平均流速。

本文选用长江流域内155个互不嵌套的源头型中小流域(图1)，面积介于33～3 790 km2之间。每个流域内收集不少于30场次历史洪水资料，通过上述方法，利用下列公式[11,12]，确定流域最优表征的平均流速。

(1)

(2)

(3)

式中：v为平均流速，m/s；RA为霍顿面积比；RB为霍顿分叉比；RL为霍顿河长比；LΩ为最高级河道长度，m；k、a为中间变量；Γ(a)为x的伽马函数；t为计算时段长。

图1 研究区域及站点分布示意Fig.1 Indication of research watershed and hydrology stations

1.2 流域地形地貌参数

流域的地形地貌参数是流域下垫面条件在空间分布的一种数值表示方式。基于30 m×30 m精度的数字高程模型(DEM)，利用Rivertoools4.0[13]工具提取出每个流域上的最大河长、河网密度和面积比等共计17个地形地貌参数(表1)。

表1 流域地形地貌参数重要性排序Tab.1 Importance Ranking of basin topographic and geomorphological parameters

注：*表示通过95%的置信度检验。

1.3 重要性评价

流域的水文响应是降水和下垫面条件综合作用的产物，当降水条件一定时，流域的地形地貌特征对流域水文响应有着重要影响，其中的一方面就体现在对流域平均汇流速度的作用上。为探讨流域地形地貌特征对其平均流速的影响关系，本文从所有流域中随机挑选出了117个流域，分别利用Spearman相关性分析和随机森林模型[14]两种方法综合分析流域最优表征的平均流速和地形地貌参数之间的相关性，并且根据它们之间的相关性指标进行重要性排序。地形地貌参数排序越靠前，代表其对流域平均流速的影响程度越大，即流域的平均流速主要受到该地形地貌参数的作用和控制。同时，不同的地形地貌参数具有不同的量纲，会影响其与平均流速之间的相关性，因此在相关性分析之前通过数据标准化处理来消除地形地貌参数的量纲影响。分析和排序结果如表1所示。

(1) 利用Spearman相关性分析时，地形地貌因子的重要性顺序是按照其与平均流速之间的相关系数大小进行排序的。其中，最高级河流的海拔落差、最高级河长和高宽比都通过95%的置信度检验，并且与最优表征平均流速的相关性最高，说明它们对最优表征平均流速的影响作用最大；其余的地形地貌因子均未通过检验。

(2) 利用随机森林模型分析时，通过优选确定模型中的特征变量个数mtry 和树的数目ntree的取值分别是15和1 000，最终输出是按照均方误差的平均递减和精确度平均递减对参数的重要性排序的结果，递减的数值越大表示因子对流域平均流速的影响越大。根据随机森林模型的均方误差和精确度评价结果来看，对流域平均流速影响程度最大的地形地貌因子都是最高级河流海拔落差和最高级河长，并且其在综合评价中也处于十分重要的位置。

根据地形地貌参数的各个重要顺序的累加结果重新进行排序，得到各地形地貌参数对流域平均流速影响程度的综合重要性顺序。根据综合排序结果来看最高级河流的海拔落差和最高级河长是影响流域平均流速最重要的地形地貌因子，即在流域平均流速的形成上主要受到它们的作用。因此最终选择构建最高级河流海拔落差和最高级河长与流域平均流速的相关关系。

1.4 相关关系的建立

根据1.3节的分析结果，以率定流域最高级河流的海拔落差和最高级河长为自变量，流域最优表征的平均流速为因变量，通过Eureqa工具进行函数关系拟合并优化后得到式(4)。从式(4)的表达形式来看，最高级河流的海拔落差越大，平均流速的数值越大，而最高级河长正好相反，这种关系符合实际的情况。并且，最高级河流的海拔落差比最高级河长对平均流速的影响更大，这种影响关系也与上述相关性分析得到的结果一致。

(4)

式中：v为平均流速，m/s；DΩ为最高级河流海拔落差，m；LΩ为最高级河长，km。

利用公式(4)计算剩余38个流域相应的流速，得到的结果记为Vc，并与上述求得的最优表征平均流速Vs进行对比检验。如图2所示，率定流域和验证流域的拟合效果良好，确定性系数分别为0.557和0.588，表明利用公式(4)计算的平均流速在率定和验证流域上均适用，并且能够用于计算流域的平均流速。

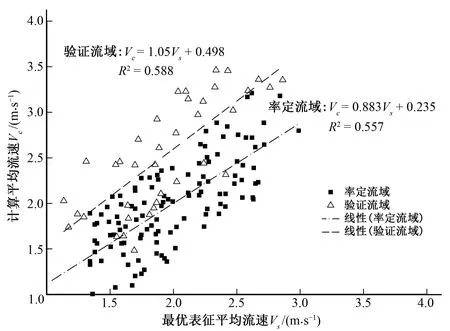
图2 率定和验证流域的最优表征平均流速和 计算平均流速的相关关系Fig.2 Scatter plots and correlation of calculated average flow velocity and optimal characterized average flow velocity in calibrated and validated basins

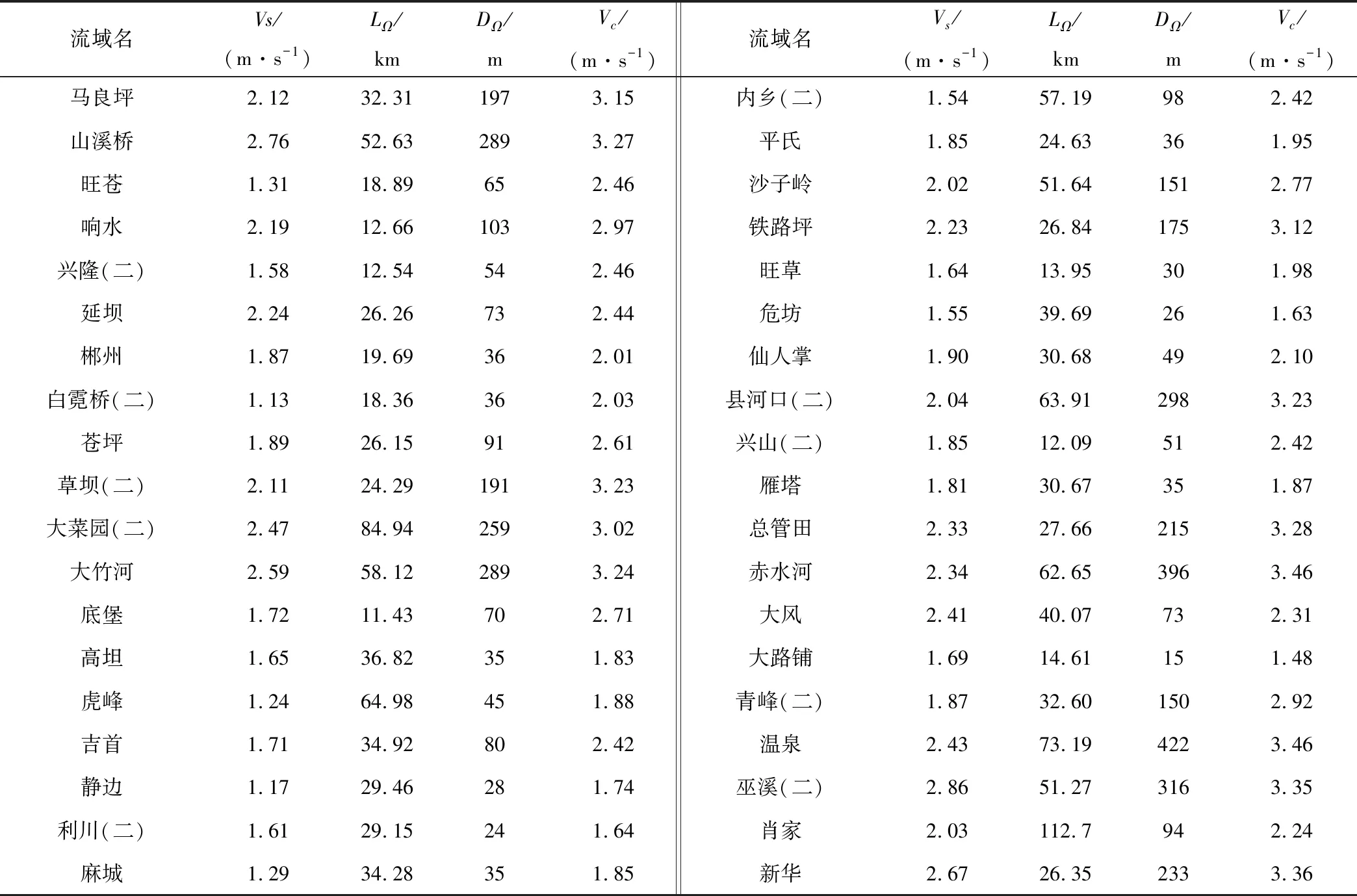
表2 38个验证流域的计算平均流速Vc与最优表征平均流速Vs数值Tab.2 Calculated average flow velocity and optimal characterized average flow velocity in 38 validated watersheds

2 实例应用

为了进一步探讨本文提出的确定平均流速方法在地貌瞬时单位线中的适用性，选取了海南省定安河流域进行验证，并与传统新安江模型的计算结果进行对比。

2.1 应用流域概况

定安河流域地处海南省境内，属于万泉河的一级支流，流域控制面积约1 257 km2，主河道全长约99 km。受热带季风气候的影响，流域暴雨季节性明显，多年平均降水量约为1 639 mm。流域山地起伏较大，短历时强降雨易造成山洪暴发。流域基本信息及所使用的历史洪水资料系列统计见表3，场次洪水资料的时间步长均为1 h资料。

表3 流域概况及其水文资料统计Tab.3 Characteristics and hydrological data statistic of watersheds

2.2 结果分析

利用流域30 m×30 m的DEM提取地形地貌参数，通过式(4)计算出流域的平均流速为2.81 m/s。从计算结果来看，平均流速的数值大小符合实际情况[15]，可以用于场次洪水的模拟计算。

在模拟计算的过程中，首先使用日模资料对模型的蒸散发和产流参数进行率定和检验，选用径流深相对误差和确定性系数作为目标函数；然后使用场次洪水资料对新安江模型的其他参数进行率定，将综合误差系数作为场次洪水计算时的目标函数。在检验平均流速的适用性时，不改变模型的其他参数，将地表径流直接汇入河网，利用地貌瞬时单位线模拟水体从进入河网到流域出口的汇集过程。模拟结果及误差统计见表4。

由表4可知：新安江模型的平均洪峰误差为12.7%，平均确定性系数为0.725；地貌瞬时单位线模型的平均洪峰误差为10.35%，平均确定性系数为0.741。由此可以看出，地貌瞬时单位线模型与新安江模型的计算结果相近，甚至稍微优于新安江模型的计算结果。尤其在洪峰滞时方面，从原来的平均峰现时差为3.8 h，降低到了1.9 h，并且其中有9场洪水的时差在1 h以内，占场次洪水总场数的50%。

综合上述分析，通过本文的确定流域平均流速方法[式(4)]计算得到的流域平均流速，数值范围符合实际情况；根据其计算出的流域地貌瞬时单位线模拟历史场次洪水过程的结果显示，计算效果良好，能够用于实际的洪水预报业务。

表4 模拟结果及误差统计Tab.4 Accuracy statistics of hourly simulation results

注：平均值一栏为各项绝对值的平均值，非直接相加求平均。

3 结 语

基于地形地貌参数的地貌瞬时单位线是解决无资料或资料匮乏地区汇流计算的一种非常有效的方法。针对现有研究中对于地貌瞬时单位线中汇流速度确定方法研究的不足，本文通过对地形地貌参数和流域平均流速进行相关性分析，建立仅与地形地貌参数相关的确定流域平均流速的方法，主要结论如下：

(1)通过率定优选的方式确定流域最优表征的平均流速，以此代表流域实际的平均流速。应用Spearman相关性分析法和随机森林模型综合分析了流域最优表征的平均流速和地形地貌参数之间的相关关系。结果表明，最高级河流的海拔落差和最高级河长是影响流域平均流速最重要的地形地貌因子。

(2)以率定流域的数值信息建立最优表征的平均流速与最高级河流的海拔落差、最高级河长的相关关系式，并在率定流域和验证流域上进行验证，结果表明，计算的平均流速 和最优表征的平均流速 之间的拟合效果良好，确定性系数分别为0.557和0.588，即利用公式(4)确定的流域平均流速能够代表流域实际的平均流速。

(3)将本文研究的计算方法应用到海南定安河流域，构建地貌瞬时单位线模型模拟历史场次洪水，并与传统新安江模型进行对比。根据计算结果，计算的平均流速数值符合实际情况，模拟计算的各项指标的误差均在允许范围内且模拟的洪水效果优于传统新安江模型，特别是在峰现时差方面有明显的提高。

□