在反思和追根中提升解题教学效益——以一道向量题为例

林 松

(江苏省仪征市第三中学 211400)

数学习题“题海无边”，如果解题和解题教学就题论题，则永远做不完、讲不尽．解题和解题教学只有“回头是岸”，加强解题后的回顾反思和追根求源，才能跳离题海、事半功倍，提升解题和解题教学的效益．这里的反思和追根是对解题思路、问题本质进行反思和求源．通过反思与追根利于学生数学核心素养的培养和落实．下面以一道向量题为例进行一番反思和追根．

1 习题的呈现

图1

此题是一道平面向量数量积运算问题，是平面向量的核心内容．此题蕴含丰富的数学思想和方法，如转化思想、数形结合、特殊化等，是落实数学核心素养难得的知识载体．在教学中应让学生充分展示解题思路，引导学生对解题的思路进行反思，对问题的数学本质进行挖掘，探索数学问题的根源，激发学生的学习兴趣，提升学生的数学素养．

2 学生思路展示及反思

2.1基底法思路及反思

(1)思路

教学中，学生认为基底法是解决向量问题的常用方法，展示了如下解法：

(解法一)如图2，

①

②

图2

因为点M、N分别是边AD、BC的中点，所以

所以由①+②可得，

(2)反思

2.2坐标法思路及反思

(1)思路

图3

(解法二)以N为原点，BC所在直线为x轴建立如图3所示的直角坐标系．

设B(-x0,0)，C(x0,0)，A(x1,y1)，D(x2,y2)，

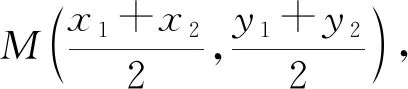
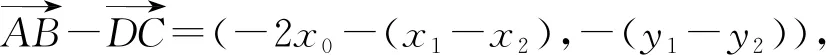
又因为AB=DC，

(2)反思

教学中应引导学生反思以下问题：①坐标法解决向量问题的本质是什么？②解题过程中是如何实现简化运算的？通过引导学生反思，理解用坐标法处理向量问题也是一种常见思路，其本质上就是几何问题代数化．应注意引导学生对条件和目标进行差异分析，确定计算方向，简化运算，培养学生的数学运算素养．

2.3 直观猜想法思路及反思

(1)思路

图4

证明：如图4，取AC的中点K，连接MK、NK．

因为M、K分别为AD、AC中点，

所以MK

所以∠CQN=∠KMN．

同理KN

所以∠KNM=∠BPN．

又因为AB=CD，所以KN=KM，

所以∠KMN=∠KNM，所以∠CQN=∠BPN．

(2)反思

平面几何知识具有“形”的直观，与高中数学中的平面向量具有相同的本质．在解决一些关于平面向量问题的试题时，可以结合平面图形的性质，利用平面几何的知识去解决，可以另辟蹊径，换一个思路解决问题，落实了学生直观想象和逻辑推理素养．

通过反思，学生可以利用“∠CQN=∠BPN”，结合向量数量积定义可得到原题如下创新解法：

(解法三)如图4，设∠BPN=α，∠CQN=β，则α=β．

图5

(解法四)如图5，还可以利用几何方法得到如下解法：

作BR，使BRDC，作∠PBR的角平分线BT交PN于T，可得∠CBR=∠C，∠PBT=∠RBT．在△BPT和△BNT中，因为

∠BTP=180°-(∠PBT+∠BPT),

∠BTN=180°-(∠NBT+∠BNT)

=180°-(∠NBT+∠C+∠CQN)

=180°-(∠NBT+∠CBR+∠CQN),

所以∠BTP=∠BTN.

又∠BTP+∠BTN=180°,

所以∠BTP=∠BTN=90°.

因为∠BTP=∠BTN=90°,

2.4 特殊化法思路及反思

(1)思路

图6

(2)反思

错误的思路有时也有可以汲取营养的地方，有时也有反思讨论的价值．上述特殊化法虽然不合题意，但如此特殊化得出正确的答案是偶然的还是必然的呢？是否具有合理性呢？现在已经证得“∠BPN=∠CQN”，那么上述特殊化也是合理的，极致特殊化的图形其实就是后文实验操作的起始图形，亦可以看作是极限位置，得到正确答案是必然的．

3 数学实验与追根

教学中，由“∠BPN=∠CQN”的发现，可以追溯本题题图的来源．引导学生开展以下实验操作得到．

①如图7，取两个相等的角∠UPV，∠XQY的纸片，让∠UPV的顶点P与∠XQY的顶点Q重合，∠UPV的边PV和∠XQY的边QX重合；

图7

图8

图9

②如图8，在PU，PY上分别取A、B，D、C，使得PA=PD，AB=DC，连接AD，BC分别交PX于M、N．再沿着边PV向下移动∠XQY，在PU与QY上分别截取PA=QD，PB=QC，连接AD交PV于M，连接BC交PV于N，此时就得到图9的一般情况．

由上面的操作可以知道：只要∠BPN=∠CQN，PA=QD，AB=DC，就应有M、N是AD、BC的中点．反之，AB=DC，M、N是AD、BC的中点，一定有∠BPN=∠CQN，PA=QD．

4 教后的思考

《普通高中数学课程标准(2017年版)》指出：“向量是描述直线、曲线、平面以及高维空间数学问题的基本工具，是进一步学习和研究其他数学领域问题的基础，在解决实际问题中发挥重要作用．”[1]可见，向量的学习对高中生数学素养发展的意义重大．教学中，应引导学生理解在高中数学中解决向量问题的主要方法基底法和坐标法，基底法和坐标法的共同本质在于把图形关系转化成代数关系，利用代数运算去解决问题，实现数与形的转化．其实，坐标法是基底法的特殊化，就是单位正交基底法，而用坐标来处理之后的几何问题在求解过程中，特别是在求某个点的坐标时，大多情况下会更加方便自然，可操作性强．平面几何的方法在解决一些关于平面向量问题时，可以另辟蹊径，也能很方便解决地解决问题，甚至有意想不到的收获．当然，平面几何的方法对解决向量问题时更多地是起到辅助的作用，绝不能喧宾夺主，过分强调其作用．