学习进阶为不同课型“把脉”*

江苏省宜兴市丁蜀高级中学 毛燕平

学习进阶理论旨在为学生的认知发展建模，形成可持续发展的数学核心素养.学习进阶理论强调围绕核心概念或研究主题，建构一系列前后一致、逻辑连贯的思维序列，让学生自主选择合适的认知路径，循序渐进，层层深入，逐步走向深度学习的高层次阶段.

以教学改革为名而推出的评优课、示范课、精品课自然吸引了很多人的关注，起到教学引领作用的示范课自然不能轻视，但师生双方均会因为听课者的出现而在注意力上有所分散.笔者以为，师生每天都会经历的常态课往往会因为学生所受限制较少而呈现出更加默契的师生交流.本文结合同一教材的示范课与常态课的教学片段进行了对比分析与思考，依据学习进阶理论在各自存在的问题上进行分析并探寻了两者之间的“平衡点”.

一、以“已有认知”作为教学出发点

以学生的已有认知作为教学的出发点并引导学生在分析思考、合作探究中获取新知识，才能使学生的储备知识得到激发和挖掘并以此为“生长点”进行新知识的探究.

情境1：示范课

某教师在数列复习示范课上设计出了如下两个问题：

问题1：填写以下表格.

学生很快得出：前n 个正奇数之和等于n2；重要不等式定理为：若a，b∈R+，则（当且仅当a=b时取“=”）.

师：大家想一想应如何证明？

三分之二的学生在问题1 的铺垫下顺利进行了证明，而且方法比较统一.

情境2：常态课

这是笔者推门听课所听的一节数列复习课，该执教老师作出了以下不同设计：

这位教师在随堂课上直接将上述问题抛给了学生，学生在没有任何铺垫的情况下陷入了思考僵局.

师：学生1，在此题的证明上你是如何思考的？

生1：我的思考还没成熟，不过我想从左边往右边证明，好像不好做.

师：有哪位同学能补充一下？

生2：我准备将其左边看作数列来解题的，不过也没解决.

（学生的思考明显受阻了）

师：将式子左右两边割裂是上述两位同学共同的想法，是否可以综合起来呢？

（学生激烈讨论起来，执教老师担心浪费时间，开始了直奔目标的启发）

师：什么的和是n2？我们之前学过的？

生3：前n 个正奇数之和为n2.

师：不等式左边的每一项是否可以变为奇数呢？

生4：嗯，不等式右边有（n+1）2，则前n+1 个正奇数之和为（n+1）2，想法将左边转化成前n+1 个正奇数之和就行了.

生5：数学归纳法证明也是可行的.

师：很好，这是你根据自学内容得到的证明方法，大家以后也都会运用到的.

反思：情境1 的设计明显是教师认真准备的，问题1 作出的铺垫令课堂教学的目标得以顺利完成，但问题2 所具备的潜在价值却并没有得到充分地体现.情境2忽略了学生的思维起点，学生探究的内容虽然多，但其中的认知跨度明显是学生较难适应的，这也直接导致了教师最后只能选择直接告知的教学方式.笔者以为，教师应认清学生的已有认知水平并依此进行教学情境设计，引领学生在已有认知的基础上有效回顾和深入探索，这也是教师在课堂设计中必须探究、确立的示范课和常态课的一个“平衡点”.

二、以“问题引领”作为教学落脚点

教师围绕知识目标设计的问题与问题情境能使学生在认识问题、解决问题的过程中获得数学思维能力与数学素养的提升.

情境3：示范课

某教师在教研活动中的教学片段如下：

师：已知等差数列{an}：4，7，10，13，16，…，请大家观察此数列并尝试写出其第100 项a100.

生1：a100=301.

师：怎样算的呢？

生1：我正好预习了等差数列的通项公式an=a1+（n-1）d，我将a1=4，n=100，d=3 代入公式计算了出来.

师：若没预习过，这第100 项a100又应该如何计算呢？

生1：一项一项推.

师：这是很烦琐的过程了，能找到规律吗？

生1：后一项减前一项正好都是3，其他就不懂了.

师：老师接下来就将每一项列出并写出其改写过程.

（这是教师担心课堂教学任务不能完成作出的举动）

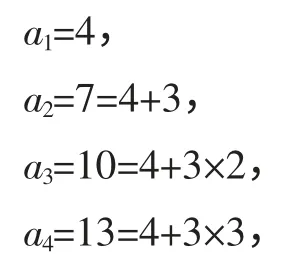
则a100=4+3×99=301.

师：从a100=4+3×99=301 的表示中，大家能猜出首项是a1、公差是d 的等差数列{an}的通项第n 项an吗？如何证明？

生2：数列{an}的通项为an=a1+（n-1）d.不过我不会证明.

师：大家还记得等差数列的定义吗？是否可从此处着手？

生3：可以的，从等差数列的定义可知，a2-a1=d，a3-a2=d，…，an-an-1=d，将以上n-1 个等式相加可得an-a1=（n-1）d，即an=a1+（n-1）d.

情境4：常态课

师：已知等差数列{an}：4，7，10，13，16，…，大家观察一下，是否可以很快写出其第100 项a100呢？

生1：我不会.

师：请大家观察以下各式并分别写出其值.

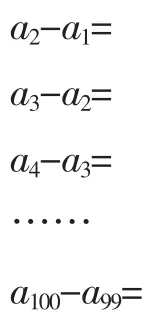
生2：都等于3.

师：那么大家是否可以对上述n-1 个式子进行整体考虑并推出第100 项的值呢？

生3：用叠加法可以求出.

师：那大家能否猜出首项是a1、公差是d 的等差数列{an}的通项an呢？怎么证明？

生4：能，根据等差数列的定义可知a2-a1=d，a3-a2=d，…，an-an-1=d，把以上n-1 个等式相加可得an-a1=（n-1）d，即an=a1+（n-1）d.

反思：情境3 中的执教老师作出了“观察——归纳——猜想——证明”的教学设计，不过因为学生没有数列的类似知识导致教师的这一设计失败了，最终教师只能自己给出改写过程.情境4 中的执教老师设计的问题情境较为简单，过于直接的问题设计并不能帮助学生对所学知识形成深刻的理解.事实上，教师如果能抓住等差数列的概念本质并设计问题情境，使学生能够在以“问题引领”的教学中进行思考与探究，必然能使我们获得示范课与常态课的又一“平衡点”.

三、以“拓展变式”作为教学生长点

以“拓展变式”作为教学生长点能使学生的学习能力与创新意识均得到很好的发展，教师在实际教学中应有针对性地进行拓展变式训练并帮助学生更好地学会应用.

情境5：示范课

师：谁会解决此题？

（学生没有表示，于是该执教老师直接提问了生1）

生1：它明显不是等差数列，所以用等差数列求和的方法是不行的，但式子看上去比较特别，应该有特殊办法，不过我不会.

情境6：常态课

教学的第一步同情境5 中的问题1，问题解决之后随即进行了拓展与变式.

拓展1：已知等差数列{an}，an≠0，公差是d，化简

拓展3：如果数列{an}对一切正整数n 均满足：，那数列{an}必然为等差数列吗？如果是，请证明；如果不是，能举出反例吗？

反思：存在多处限制的情境5的教学相对呆板，学生的思维和能力生长也因此丧失.情境6 的教学却能摆脱各种限制并进行拓展，新的知识生长点因此形成，但教学容量相对过大，很多学生对拓展变式的理解与把握未必深入.事实上，教师若能在学生掌握“裂项求和”的基础上进行拓展1、拓展2 的训练，有效资源“生长点”的有效应用必然使示范课与常态课之间再获新的“平衡点”.

总之，教师应以“已有知识”为教学的出发点并进行问题情境的设计与拓展变式的训练，使示范课与常态课之间处于平衡、稳定的状态并获得课堂教学的理想效果.W