寻根究源,还原本“意”
——一道圆锥曲线试题的命题背景探索
江苏省海门中学 李乃洋
圆锥曲线问题在高考或者竞赛初赛试题中出现频率较高,究其原因是其丰富的几何特性与其解法的无穷魅力.在解决问题时,有时我们还需更多思考命题者的命题源头或者背景是什么,往往在一番探索之后,会对圆锥曲线理解更深一层.最近笔者在解决一道数学初赛试题时,尝试思考出题人出于何种命题的“依据”,于是带着这个思考做了如下探索.
一、试题呈现
二、解法探究
方案一:利用直线的参数方程简化计算.
解法1:因为焦点F(c,0),设直线l的倾斜角为α,则直线l的参数方程为(t为参数),且A,B对应的参数分别为t1,t2,将直线的参数方程代入双曲线的方程得:
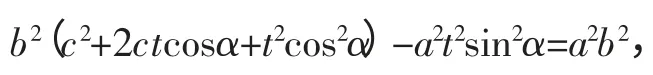
化简为(c2cos2α-a2)t2+(2b2ccosα)t+b4=0,

因为|OF||AB|=|FA||FB|,所以c|t1-t2|=|t1|t2|,将上述结果代入化简得2ac=b2,依据双曲线中b2=c2-a2,可知e2-2e-1=0,又e>1,所以e=
方案二:利用双曲线的极坐标方程简化计算.
解法2:以双曲线的右焦点F为极点,x轴正方向为极轴建立极坐标系,则双曲线的右支方程为(ρ>0),左支方程为,其中p为该焦点到对应准线的距离(焦准距).如下图(考虑两种情形)
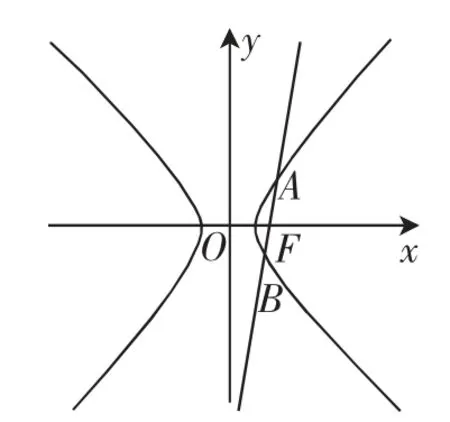
图1-1

图1-2
(1)在图1-1中,交点位于右侧同支,设点A(ρ,θ),则
(2)在图1-2中,如果交点位于两侧不同支,如交点A在右支,而B在左支,则(此时e2cosθ2>1).
代入|OF||AB|=|FA||FB|得:
以下同解法1,结果可知e2-2e-1=0,又e>1,所以e=
解法反思:上述解法均是建立在圆锥曲线中焦半径不同表示方式基础之上,依据圆锥曲线第二定义(统一定义)解题.试题中条件“|OF|·|AB|=|FA|·|FB|”包含了焦半径|FA|,|FB|,以及焦点弦长|AB|和半焦距|OF|这些几何量,探究其与曲线离心率e的数量关系,自然让我们思考试题命制的背景是什么?
三、试题背景
事实上,对于等式|OF|AB|=|FA||FB|做一变形,即|OF|·(|FA|+|FB|)=|FA|·|FB|可得而对于表达式,其含义我们熟悉表示圆锥曲线共线焦半径的倒数和,通常其和为定值为焦准距,e为离心率),于是我们以抛物线为例论证其关系(焦点在x正半轴,如图2).
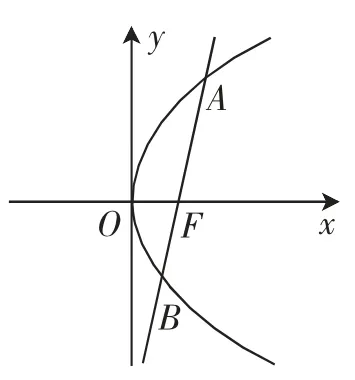
图2
结论1:已知抛物线顶点在坐标原点,焦点F在x正半轴上,过焦点F的直线交抛物线于点A,B,则
类比抛物线,我们也可以得到椭圆中结论.
(证明略)
一般在圆锥曲线中,很多性质具有统一性,自然思考上述结论在双曲线中是否成立?在解法2中,事实上我们已经得到如下两种情形:
比较三种圆锥曲线上述结论形式,我们一定思考,如何将具有和谐统一的圆锥曲线结论统一,于是从产生异化的双曲线入手,其实,但是要考虑抛物线的离心率e=1,故我们可以把上述关系再整理,得到
定理:已知焦点在x轴上的圆锥曲线(中心在坐标原点),过x正半轴上的焦点F的直线l与曲线交于不同两点A,B,焦准距为p,离心率为e,则焦点弦长|AB|与焦半径 |FA|,|FB|满足关系
由上述定理,不难发现开头这道试题的命题背景即为探索圆锥曲线中焦点弦与焦半径之间的关系,利用圆锥曲线的统一定义我们可以有多种解法,但基于双曲线的两支情形,需要关注焦点弦的特殊性,在文1等文献中,都出现了在圆锥曲线中这种定值结论,但对于双曲线来说,过焦点的直线形成的两个焦半径倒数和是不确定的(只有焦点F内分线段AB时,结论正确).基于上述分析,再结合极坐标方程,我们容易得到如下推论.
推论1:已知焦点在x轴上的圆锥曲线(中心在坐标原点),过x正半轴上的焦点F的直线l与曲线交于不同的两点A,B,圆锥曲线的离心率为e,焦点到对应准线距离为p.若直线的倾斜角为θ,则焦点弦长公式为|AB|=
推论2:已知焦点在x轴上的圆锥曲线(中心在坐标原点),过x正半轴上的焦点F的直线l与曲线交于不同两点A,B,圆锥曲线的离心率为e,焦点到对应准线距离为p.若则焦点弦长公式为
且由圆锥曲线极坐标公式(双曲线两支符号不同),可得,推论1得证.
四、结束语
通过对一道试题的探究,我们发现了圆锥曲线中一共性性质,并通过解法探究及结论的论证,进一步理解解析几何的核心“用代数的方法研究几何问题”,这正是我们解决问题需要掌握的策略,也是命题者更深的用“意”.数学家哈尔斯说过“问题是数学的心脏”,在平时解题中我们要养成“提出问题、发现问题、分析问题,解决问题”的研究手段,提升读懂、理解数学命题的能力.

