不等式恒成立，参数值妙求解——2019年全国卷Ⅰ文第20题

浙江省金华第一中学 吴贤盛

不等式中的恒成立问题能够很好地考查函数、不等式等相关知识，以及函数与方程、化归与转化等数学思想，一直备受命题者的青睐，是各级各类考试中的热点问题之一.此类问题一般位于选择题或解答题的压轴题位置，难度一般为中偏高档或高档层次.经常出现的题目类型是不等式恒成立的证明、不等式恒成立条件下的参数值或取值范围的求解等.

一、真题在线

【高考真题】（2019年全国卷Ⅰ文20）已知函数f（x）=2sinx-xcosx-x，f′（x）为f（x）的导数.

（Ⅰ）证明：f′（x）在区间（0，π）内存在唯一零点；

（Ⅱ）若x∈［0，π］时，f（x）≥ax，求a的取值范围.

本题考查导数的应用，求导公式和法则、函数的零点、不等式恒成立等知识，考查推理论证能力、运算求解能力，以及分类与整合思想、函数与方程思想等.巧妙地把导数及其应用、三角函数、函数及其零点、不等式恒成立、参数的取值范围等相关问题加以交汇与融合，综合考查知识与能力.

二、真题解析

解析：（Ⅰ）方法1：（官方标答——函数单调性法）

设g（x）=f′（x），则g（x）=cosx+xsinx-1，g′（x）=xcosx.

所以f′（x）在区间（0，π）内存在唯一零点.

方法2：（零点存在性定理法）

由题意得f ′（x）=2cosx-［cosx+x（-sinx）］-1=cosx+xsinx-1.

设g（x）=f′（x）=cosx+xsinx-1，则有g′（x）=xcosx.

所以根据零点存在性定理，可知f′（x）在区间（0，π）内存在唯一零点.

（Ⅱ）方法1：（官方标答——函数单调性法）

由题设知f（π）≥aπ，f（π）=0，可得a≤0.

由（Ⅰ）知，f′（x）在（0，π）内只有一个零点，设为x0，且当x∈（0，x0）时，f′（x）＞0；当x∈（x0，π）时，f ′（x）＜0.所以f（x）在（0，x0）上单调递增，在（x0，π）上单调递减.

又f（0）=0，f（π）=0，所以，当x∈［0，π］时，f（x）≥0.

又当a≤0，x∈［0，π］时，ax≤0，故f（x）≥ax.

因此，a的取值范围是（-∞，0］.

方法2：（构造函数法）

若x∈［0，π］时，f（x）≥ax，即f（x）-ax≥0恒成立.

设函数h（x）=f（x）-ax=2sinx-xcosx-（a+1）x，则h′（x）=cosx+xsinx-1-a，h″（x）=xcosx=g′（x）.

①当a≤-2时，h′（x）min=h′（π）=-2-a≥0，即h′（x）≥0在区间［0，π］上恒成立，则h（x）在区间［0，π］上单调递增，则有h（x）≥h（0）=0，即f（x）-ax≥0，此时f（x）≥ax恒成立.

又h（0）=0，h（π）=-aπ≥0，则知h（x）≥0在区间［0，π］上恒成立，即f（x）≥ax恒成立.

所以，当x∈［0，x2）时，h（x）＜h（0）=0，可知f（x）≥ax不恒成立.

综上分析，可知a的取值范围是（-∞，0］.

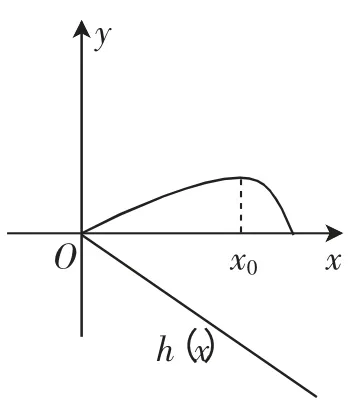
图1

方法3：（数形结合法）

由（Ⅰ）知，f′（x）在区间（0，π）上存在唯一零点x0，使得f′（x0）=0，且当x∈（0，x0）时，f ′（x）＞0；当x∈（x0，π）时，f′（x）＜0.

所以f（x）在（0，x0）上单调递增，在（x0，π）上单调递减.

又f（0）=0，f（π）=0，所以，当x∈［0，π］时，f（x）≥0.

设函数h（x）=ax，作出函数图像，如图1所示.

由于f（x）≥ax=h（x）在区间［0，π］上恒成立，则有a≤0.

因此，a的取值范围是（-∞，0］.

方法4：（分离参数法）

若x∈［0，π］时，f（x）≥ax，等价于2sinx-xcosx-x≥ax（*）在区间［0，π］上恒成立.

①当x=0时，（*）式即为0≥a×0，显然成立，此时有a∈R.

②当x ≠0 时，即x ∈（0，π］，（*）式可化为a ≤

设函数h（x）=2xcosx-2sinx+x2sinx，则h′（x）=x2cosx，x∈（0，π］.

当x∈（0，x0）时，g′（x）＞0，g（x）单调递增；当x∈（x0，π］时，g′（x）＜0，g（x）单调递减.

综上分析，可知a的取值范围是（-∞，0］.

三、规律总结

破解此类含参不等式恒成立问题的方法较多，比较常见的思维方式就是利用分离参数法来处理，在能够判断出参数的系数的正负的情况下，可以根据不等式的性质将参数分离出来，得到一个一端是参数，另一端是变量表达式的不等式，只要研究变量表达式的最值即可.此时，求解含参不等式恒成立问题的关键是过好“双关”：第一关是转化关，即通过分离参数法，先转化为f（a）≥g（x）（或f（a）≤g（x））对任意x∈D（定义域）恒成立，再转化为f（a）≥g（x）max（或f（a）≤g（x）min）；第二关是求最值关，即求函数g（x）在区间D上的最大值（或最小值）问题.

而有些含参不等式恒成立问题，在分离参数时会遇到讨论的麻烦，或者即使分离出参数，但参数的最值却难以破解，此时常借助导数法，通过求导，分析函数的单调性，通过对函数单调性的分析确定函数值的变化情况，找到参数满足的对应的不等式，往往也能取得意想不到的效果.