基于数学探究性学习的教学设计*——以“探究隐圆之源”为例

四川省自贡市教育科学研究所 张德荣

四川省绵阳南山中学校 何先俊

数学探究是中学数学教学核心内容之一，探究性学习经历了一个从他主到自主的发展过程，探究性学习既需要能学、想学、会学、坚持学的内部条件，更需要教师指导的外部条件.数学探究性学习分为课堂内的探究性学习、课堂外的探究性学习及课堂内外相结合的探究性学习三种.本文就学生课堂内外相结合的探究性学习下的教学设计谈一些想法.注：本堂课是高三第二轮复习课，学生是成绩中等的理科班学生，有一定的自主学习与自主探究能力.

一、提出问题

（一）问题背景

古希腊数学家毕达哥拉斯曾说：“圆是一切平面图形中最美的图形.”但在数学解题时，我们往往发现不了美丽的圆，因为很多时候圆是隐藏着的，但高考又经常在此考点进行考查，故我们有必要对这些知识进行归纳、总结.

“隐圆”，顾名思义，即隐藏着的圆，发现“隐圆”不仅需要一双“发现美的眼睛”，更需要有扎实的数学基础.现在让我们去发现各类隐圆，发掘隐圆之源，探究其解法，领略圆之美.

（二）明确任务

各位同学请在课外收集整理与“隐圆”相关的概念、试题，可以翻阅教材、查看近几年的高考试题，也可以利用网络工具，时间一周.

二、前期准备

（一）探究内容

（二）学生分组

全班61人中，收集情况如下：

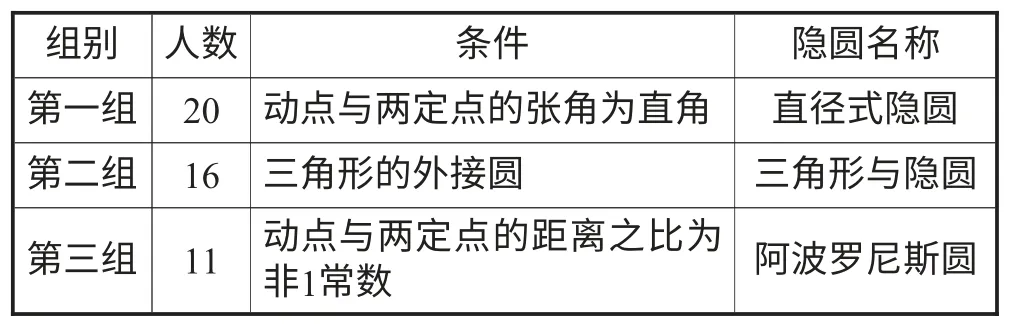
将学生进行分组，研究同一问题的学生分为一组，进行探究，没有成果的学生分入人数较少的一组.并根据所选试题的特征对各组的隐圆进行命名.其中阿波罗尼斯圆由老师所命.

（三）展示要求

每个小组指定一名组长，由组长牵头，再进行课外探究，对收集的题型进行整理，提炼典型例题、变式题，发现共性及一般性定义与解法.并制作简略的投影文档.

三、教学过程

（一）第一组：直径式隐圆

隐圆来历S1：我们做了很多张角为直角的试题，其中多数都可以用圆的相关知识解决.因为圆的直径所对的圆周角为直角，其逆命题也成立，即在平面内给定两点A、B，设点C在同一个平面内且满足∠ACB=90°，则点C在以线段AB为直径的圆上.

S2：我是从教材必修2第124页上的一道作业题的证明过程得到启发的：

已知圆的一条直径的端点分别是A（x1，y1），B（x2，y2），求证此圆的方程为（x-x1）（x-x2）+（y-y1）（y-y2）=0.此题的证明用直径所对的圆周角是直角立即得到答案.

例1 （2014年北京卷7）已知圆C：（x-3）2+（y-4）2=1和两点A（-m，0），B（m，0）（m＞0）.若圆C上存在点P，使得∠APB=90°，则m的最大值为______.

解：由直径式隐圆知，点P的轨迹是以AB为直径的圆，于是此圆与圆C有交点，可知正确答案为6.

T：必须满足张角是90°，才能用圆的方程进行解决吗？

S3：不一定，当张角大于90°或小于90°时，动点轨迹是圆外或圆内的区域，一样可以解决.

（二）第二组：三角形与隐圆

隐圆来历S1：我是由三角形的正弦定理想到三角形的外接圆的.在△ABC中，角A，B，C所对的边分别是a，b，c，根据正弦定理，△ABC外接圆的直径

例2 （2014年全国卷Ⅱ文12）设点M（x0，1），若在圆O：x2+y2=1上存在点N，使得∠OMN=45°，则x0的取值范围是______.

解：｜ON｜=1，∠OMN=45°，由正弦定理知△OMN的外接圆直径所以

T：本解法巧妙地避开了对极限位置的讨论，准确而简洁.其关键之处是什么？

S2：我认为本题关键之处是运用正弦定理求出△OMN的外接圆直径为定值，然后再根据线段OM的长度不大于外接圆直径建立不等关系，从而求出x0的取值范围.

（三）第三组：阿波罗尼斯圆

隐圆来历S1：我是受必修2第124页B组第3题的求解过程推向一般而得到的.

S2：我是直接由必修2第144页B组第2题得到的.

T：以上两位同学所说的圆有一个很好听的名字“阿波罗尼斯圆”.古希腊数学家阿波罗尼斯（约公元前262—前190）在其著作《圆锥曲线论》中有一个著名的几何问题：“在平面内给定两点A，B，设点P在同一个平面内且满足当λ＞0且λ≠1时，点P的轨迹是个圆.”我们称这个圆为“阿波罗尼斯圆”，简称“阿氏圆”.

例3 （2013年江苏卷17）在平面直角坐标系xOy中，点A（0，3），直线l：y=2x-4.设圆C的半径为1，圆心在l上.

（Ⅱ）若圆C上存在点M，使｜MA｜=2｜MO｜，求圆心C的横坐标a的取值范围.

解：（Ⅱ）可设圆心C的坐标为（a，2a-4），则圆C的方程为（x-a）2+［y-（2a-4）］2=1.

因为｜MA｜=2｜MO｜，可得点M的轨迹方程为x2+（y+1）2=4，设为圆D.由条件知圆C和圆D有交点，所以｜2-1｜≤解得a的取值范围为

四、开放性探究

（一）“蒙日圆”的探究

T：前面我们研究了三种隐圆，还有同学有其他结论吗？

S1：老师，我在做2014年广东卷第20题时，发现一个结论：

T：很好，经查，椭圆的任意两条互相垂直的切线的交点在同一个圆上，这个圆我们称之为“蒙日圆”.请同学们自己完成其证明.

例4 设直线l：3x+4y+a=0，圆（x-2）2+y2=2.若在直线l上存在一点M，使得过点M能作圆的两条互相垂直的切线，则a的取值范围是______.

解：由题意知点M在圆（x-2）2+y2=4上，所以直线l：3x+4y+a=0与圆（x-2）2+y2=4有交点，于是所以-16≤a≤4.

评注：圆或椭圆的两条互相垂直的切线的交点在一个圆上；对于抛物线，交点在准线上；对于双曲线=1（a＞b＞0）的任意两条互相垂直的切线的交点在圆x2+y2=a2-b2上.

（二）勾股圆的探究

T：还有同学有其他结论吗？

S1：因为圆的标准方程是（x-a）2+（y-b）2=r2（r＞0），其结构是一组勾股数，于是我大胆猜想：已知定点A，B，若动点P满足｜PA｜2+｜PB｜2=r2，则动点P的轨迹为一个圆.

T：不错，猜想往往是发现真理最重要的一步，请同学们对此结论进行探究.

S2：老师，我得到的结论是：

已知点A（x1，y1），B（x2，y2），若动点P（x，y）满足｜PA｜2+｜PB｜2=r2，则动点P的轨迹为一个圆，其方程为2x2+2y2-2（x1+

T：请给这个圆取个名字吧.

S3：因动点P满足的式子类似于勾股定理，故我称动点P的轨迹为“勾股圆”.

T：非常形象的名字.

五、数学探究教学设计的模型

数学探究式教学是在新课标理念指导下，对数学教学方式的一次重大改革，通过开展探究性教学，学生的探究意识和创新能力得到提高，老师的教学理念和教学方法也有了很大改进.F