培养高中生思维品质的案例与思考*

江苏省天一中学 潘 干

思维能力与品质是智力发展的核心和支柱，数学知识在人的发展中或许会被遗忘，但数学学习过程中形成的思维品质却始终会对其一生产生深远的影响.高中学生思维的灵活性、敏捷性、深刻性、广阔性、批判性、独创性会在数学学习中获得飞速发展，高中数学教师应着眼于将学生数学思维品质的发展落实到有意义的数学思考、教材钻研和教法探究.

一、思维灵活性的培养

视野开阔并能多维发散是思维灵活性的具体体现，一般来讲，一题多解、一题多变是培养学生思维灵活性的常用手段.

1.一题多解

习题课教学是发展学生思维多维发展的有利平台，教师应对习题进行仔细的斟酌并引导学生运用所学知识提出不同的解题构想，引导学生对知识之间的纵横联系进行梳理与构建并挖掘出更加简捷、巧妙的解法.

例1 已知

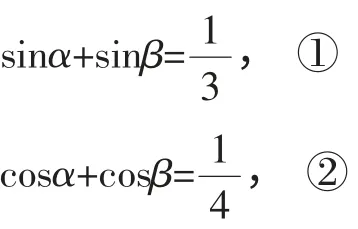
请探讨可能产生的结论？

探索1：①2+②2可得两角差的余弦公式）

探索2：①×②，再和差化积得sin（α+β）［cos（α-β）+

探索3：①2-②2，再和差化积得2cos（α+β）［cos（α-β）

探索5：由sin2α+cos2α=1消去α可得消去β可得

开放题的引入能引导学生对题目条件、条件之间的关系、结论均展开不同深度与层次的思考，帮助学生在综合变换解题手段中提升思维的灵活性.

2.一题多变

确定问题结构并对已知条件进行变形以培养学生思维的灵活性.

由等差数列的通项公式an=a1+（n-1）d，知道其中三个变量即可求得第四个变量.如“{an}是等差数列，a1=1，d=-2，则常数-9是第几项？”给予充分的空间并引导学生自主编题，学生只有全面掌握所涉及的知识才能在变式编题中更显游刃有余.随心所欲，胡编乱造显然会闹出笑话.一旦学生将上题改成“a1=1，d=-3，则常数-9是第几项？”求得自然是不对的.给予学生足够的空间并尝试自主变式编题能使学生更好地理解n∈N*，以及等差数列及其求和公式的知识，思维也更灵活.

二、思维深刻性的培养

善于从事物现象中发现本质并揭示事物关系与联系中的规律即为思维深刻性的体现.

例2 方程sinx=lnx的解有（ ）个.

A.1 B.2 C.3 D.4

分析：利用解方程解题是学生的常规想法，但却在此题上行不通.换角度思考：此题实质上就是求方程组的公共解，利用数形结合的思想串联知识并挖掘事物的本质可使此题得解，发展了学生思维的深度.

三、思维广阔性的培养

培养学生思维的广阔性就是要引导学生在充分分析题意的基础上，调动、选择相应知识对问题展开全面的分析并寻求解题关键.

例3 已知某二次函数的对称轴是直线x=-1，其图像在y轴上的截距是2，在x轴上截得的线段长是4，求二次函数的解析式.

解法1：截距是2，因此选择一般式方程y=ax2+bx+c（a≠0），有c=2，结合其他条件，列方程组即可解得a、b.

解法2：因对称轴是直线x=-1，选择顶点式方程y=a（x-m）2+k（a≠0），有m=-1，结合其他条件，列方程组即可解得a、k.

另外，根据图像的对称性可得，该函数与x轴相交于点（1，0）、（-3，0）.

解法3：根据截距是2，即过（0，2）、（1，0）、（-3，0）三点，选择一般式方程y=ax2+bx+c（a≠0），代入点的坐标，列方程组即可求得a、b、c的值.

解法4：联想一元二次方程、二次函数的关系并选择两根式y=a（x-x1）（x-x2）（a≠0），则x1=-3，x2=1.根据截距2，求得a的值.

四、思维敏捷性的培养

具备快速而准确的思维品质能使运算与推理过程更为简捷.

例4 已知某平行四边形的相邻两边边长是a和b，绕a边旋转所得几何体的体积是V1，绕b边旋转所得几何体的体积是V2，则V1∶V2=（ ）.

图1

A.a ∶b B.b ∶a C.a2∶b2D.b2∶a2

分析：直接求解，如图1，可得V1=πab2sin2θ，V2=πa2bsin2θ.

但若将此平行四边形视作矩形来解题，解题则会更加简捷.

五、思维独创性的培养

新颖、善于应变的独创性思维能帮助学生获得富有个性的见解，能使学生养成自觉质疑、探索的意识.

例5 求三角式：sin210°+sin250°+sin10°sin50°的值.

解法2：令x=sin210°+sin250°+sin10°sin50°，y=cos210°+cos250°+cos10°cos50°，则x+y=2+cos40°，x-y=-cos40°-两式相加得，则原式

解法3：作直径为1的圆，构造角度为10°、50°、120°的圆内接三角形，则sin10°、sin50°、sin120°能构成三角形的三边长.

逆用余弦定理：sin210°+sin250°-2sin10°sin50°·cos120°=sin2120°，原式

评注：解法1是常规的，解法2、3则在构思上更显巧妙和独特，教师在实际教学中应给予学生充分的探索空间以促进其思维与个性的发展.

六、思维批判性的培养

不盲从、不轻信并能对思维活动的各环节进行独立分析、调整与校正，是学生具备思维批判性的具体体现.

分析：学生在解决这道典型中点弦题目时往往会想到点差法或韦达定理，求得直线方程y=2x-1，很多学生解题至此便以为结束了，但其实还需要验证判别式Δ才行，把直线方程代入双曲线方程可得Δ=-8＜0，直线与双曲线并不存在交点.

教师在培养学生思维品质的过程中，首先，注意严谨、科学的教学活动的设计与落实，充分发挥自身的主导作用并对学生始终心存期待，让学生充分感受到教师的鼓舞与期待并为了目标的实现而努力，教师对学生所持有的期待，以及落实的科学训练方法能使学生的大脑发挥巨大的潜能.其次，教师还应随时把握学生的思维动态并注意适时激疑，使学生能够产生更加积极的思维并对问题展开更深层次的思考与探究.再次，教师应善于引导学生在各种问题与结论中揭示规律，使学生能够在不断的思考、探索、辨析与总结中获得能力的提升.

总之，数学教师应该认识到数学学习对锻炼学生思维的巨大价值，有目的、有意识地设计教学活动并做到常抓不懈，从而使学生的思维品质获得全方面的发展.F