基于GPU的大规模无人机编队控制并行仿真方法*
李文光,王 强,曹 严
(北京理工大学宇航学院, 北京 100081)
0 引言
相比于单个无人机,多无人机作战具有显著的优势,比如作战半径大、侦查范围广等,因此受到很多学者的关注,成为研究的热点[1]。编队控制算法是多无人机协同作战的一项关键技术,基于一致性的协同编队控制算法是众多编队控制算法的一种,也是一种典型的分布式算法,与传统的集中式算法相比,具有通信与控制结构灵活、无人机规模不受限制等优点,因此在编队控制问题中具有重要的应用[2]。
仿真为算法的可行性验证提供了良好的手段。但是当仿真模型规模较大时,仿真耗时问题相对突出,其成为制约仿真发展的重要因素。为提高仿真效率,并行仿真凭借其高效、可重用等特点越来越多地受到青睐[3]。并行仿真的主要任务是将仿真目标分解为多个子目标并将其分布在不同处理机上同时仿真,从而提高仿真的整体效率。在大规模的无人机编队仿真中,由于无人机数量庞大,同样会面临仿真耗时长的问题。基于此,文中研究了一种并行仿真方法,并充分利用GPU强大的计算能力和高效的并行性以提高仿真效率。
1 基于一致性的协同控制建模
无人机的运动学方程为:
(1)
式中:xi(t)为无人机的位置向量;vi(t)为无人机的速度向量;ui(t)为无人机的控制向量;N为无人机数量。
(2)
(3)
ui(t)=ui-form(t)+ui-vel(t)
(4)
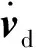
根据个体控制律式,可得系统的控制向量u(t):
(5)
式中:n为无人机模型维度,L为系统的Laplace矩阵,E与期望的编队队形相关,具体定义如下:
(6)
(7)
Li=[li1,li2,…,liN]
(8)
(9)
整理可得闭环系统的状态方程:
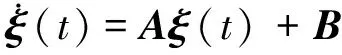
(10)
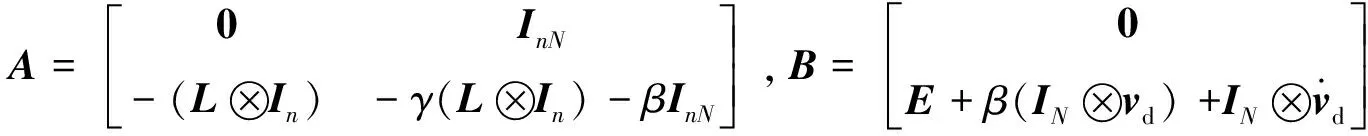
2 复杂系统的并行仿真方法
并行仿真的第一步是将整个模型拆分为多个子模型以减小模型的规模。编队控制模型是一个连续时间模型,其一般形式如式(11)所示:
(11)
而f=[f1,f2,…,fN]T为状态转移矩阵,x=[x1,x2,…,xN]T为状态向量。
连续时间模型的分割实际上就是将式(11)中的N个等式方程划分为M组,每组中的全部状态变量及其状态转移方程即组成了新的子模型Si(i=1,2,…,M)。模型分割要考虑的首要问题是降低子模型间的耦合,因为耦合是造成时延误差的关键因素。
构造N×N阶雅可比矩阵,如式(12):
(12)
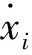
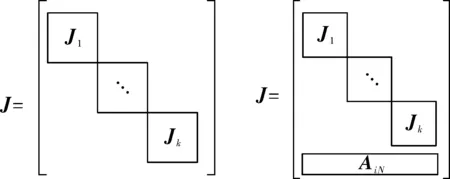
图1 矩阵变换最终结果示意图
并行仿真的第二步是将已分割的子模型分布在多个仿真机上并行求解。由于子模型间存在耦合,需要以合适的通信步长完成子模型间的数据通信。通信步长的选取至关重要,是影响求解误差的重要因素[4]。
3 GPU体系结构与CUDA
3.1 GPU及其内部体系结构
GPU(graphic processing unit)是一种扩展的计算设备,称为协处理器。与CPU相比,GPU的优势体现在其高效的并行性、强大的浮点计算能力等。
GPU的优势得益于其内部体系结构,GPU有多种架构,比如NVIDIA公司的Tesla、Fermi、Kepler、Maxwell、Pascal等等,不同GPU架构的内部体系结构略有差别[5]。以Fermi为例,其内部体系结构简化图如图2所示。
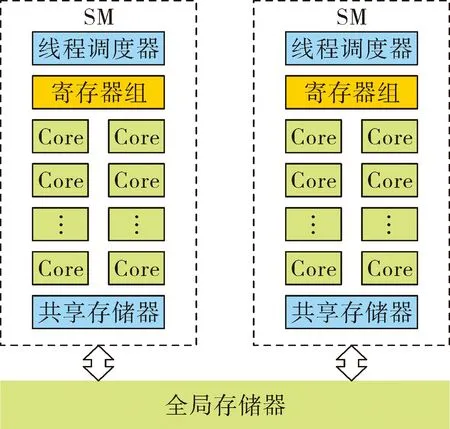
图2 Fermi架构GPU内部体系结构
图2包含了几个GPU中非常重要的结构,分别是:
1)Core:流处理器,也称为SP(streaming processor)。是GPU中最基本的计算单元,能单独完成双精度运算和32位整数运算。
2)寄存器:32位寄存器,是每个线程私有的,用于存储局部变量。
3)共享存储器:用于存储共享变量。与寄存器相比,共享存储器中的数据是一个线程块中所有线程共享的,但访问速度较慢。
4)线程调度器:用于线程调度。
5)SM:多核流处理器。一个GPU中包含一个或多个SM,一个SM通常包含线程调度器、共享存储器、多个SP以及上万个寄存器。
6)全局存储器:在某种意义上等同于GPU的显存,一个kernel函数中所有线程都能访问,存储空间大,但访问速度最慢。
虽然每个SM中有数以万计的SP,但并不是所有的SP都同时被调度。warp是SM中的线程调度单元,每个warp包含连续的32个线程,物理上占用32个SP用于计算。SM在任一时刻按照单指令多数据模式通过线程调度器执行一个warp中的所有线程,也就是说,同一个warp中的32个线程同时执行同一条指令,但分别处理各自的数据。
3.2 CUDA
CUDA是NVIDIA公司推出的编程模型,为用户提供简单的接口以实现CPU和GPU异构系统开发。
CUDA编程模型中引入主机端(CPU)和设备端(GPU)的概念,一个完整的CUDA程序包括主机端和设备端两部分代码。主机端代码在CPU上执行;设备端代码又称为kernel函数,在GPU上执行。
启动kernel函数时需要指定线程网格划分,之后CUDA运行时系统生成一个两级结构的线程网格:一个网格由多个线程块组成,每个线程块又由多个线程组成。所有线程执行同一个kernel函数,每个线程在运行时在物理上占用一个SP和多个寄存器(寄存器占用数量跟kernel函数中代码相关),因此,GPU设备对kernel函数的网格划分是有数量限定的[6]。
此外,CUDA提供了一系列函数用于操作和管理GPU设备。比如数据传输函数cudaMemcpy (),用于完成CPU与GPU间数据的传输;线程管理函数cudaDeviceSynchronize(),用于CPU和GPU间的同步等等[5]。
4 仿真设计与验证
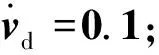
仿真实验所用计算机的CPU为Inter core i7,频率3.4 GHz,内存8 GB;GPU为Fermi体系结构,SM数量为1,Core数量为48,寄存器数量为32 768个。
4.1 模型分割
首先对模型进行分割。系统的雅克比矩阵即为式(10)中矩阵A,计算可得系统Laplace矩阵如式(13)所示:

(13)
将式(13)代入矩阵A,可以看出,每架无人机的位置向量和速度向量之间存在耦合关系;不同无人机之间一定存在且只存在与相连两架无人机的耦合。因此,同一个无人机模型的所有状态变量应通过行列置换作为一个整体,不同无人机模型按位置顺序排列。此时,在任一位置将模型分割,分割位置相连两无人机模型间的耦合即为分开后两模型间的耦合,子模型间的耦合最小。考虑到负载均衡和实验设备的限制,将整个模型拆分为5个子模型,每个子模型包含连续的200架无人机模型。
每个子模型定义如下:
(14)
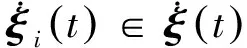
4.2 CUDA程序设计与优化
求解式(14)所示的子模型,设计的CUDA程序伪代码如图3所示。其中,kernel函数实现的功能是迭代一个仿真步长。子模型的求解采用Euler法,因此kernel函数的具体实现是计算ξi=ξi+h(Aiξi(t)+Bi+ui)。在该kernel函数中,网格划分为1×200,每个线程求解不同无人机的位置状态量和速度状态量。

图3 子模型求解CUDA伪代码
GPU中,当一个warp中的线程访问全局存储器的连续地址时,这些线程的访问请求会被合并成对连续单元的合并访问,以提高数据读取速度。基于此,考虑对上述程序优化。在kernel函数中,每个线程求解时需要获取系数矩阵A和状态向量ξ的数据。在一个warp中,32个线程同时从全局存储器中获取矩阵A的同列不同行的元素,如图4中虚线框所示,此时每个线程同时从矩阵A中读取的元素是不连续的。
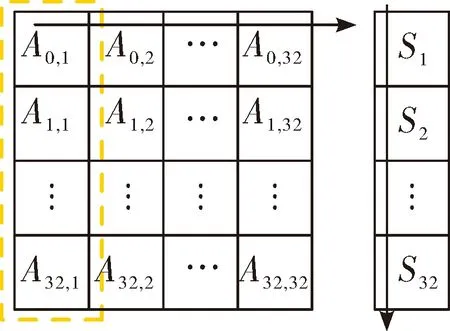
图4 优化前访问矩阵元素示意图
考虑将矩阵A转置后再复制到GPU存储器中。这时,kernel函数在计算矩阵相乘时如图5所示,同一warp中不同线程访问的是连续的元素。
将设计的CUDA程序分布到不同工作站上求解。不同工作站间的通信采用集中式通信:由另外一台计算机作为服务器,用于接受源节点的数据并发送到目标节点,并且集中控制通信步长,同步子模型的仿真时钟。仿真实验分为三组:第一组完全在CPU下求解;第二组采用未优化的CUDA程序求解子模型;第三组采用优化后的CUDA程序求解子模型。三组仿真耗时情况如图6所示。

图5 优化后访问矩阵元素示意图
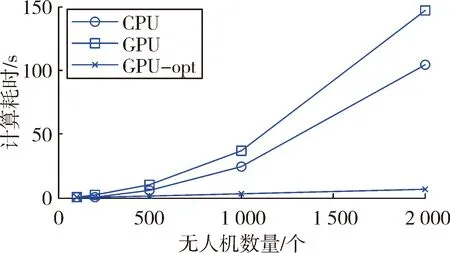
图6 CPU、GPU仿真耗时对比图
图6体现出相比CPU,GPU在求解这一类问题上更加高效,而且随着无人机规模的增大,其加速效果更加显著。同时也体现出经过优化后的CUDA程序,其效率有了明显的改善。
4.3 通信步长对误差和加速比的影响
通信步长是影响误差与仿真耗时的关键因素。为探究通信步长对误差和仿真耗时的实际影响,并为实际仿真应用中通信步长的选取提供依据,设计了本节仿真实验。实验结果如图7和图8所示,纵坐标分别为相对误差和加速比,横坐标为通信步长与仿真步长的比值,即X=H/h;相对误差是指GPU下并行仿真结果相对CPU下串行仿真结果的误差,取所有状态量相对误差的均值作为观测值;加速比是指GPU下并行仿真耗时与CPU下串行仿真耗时的比值。
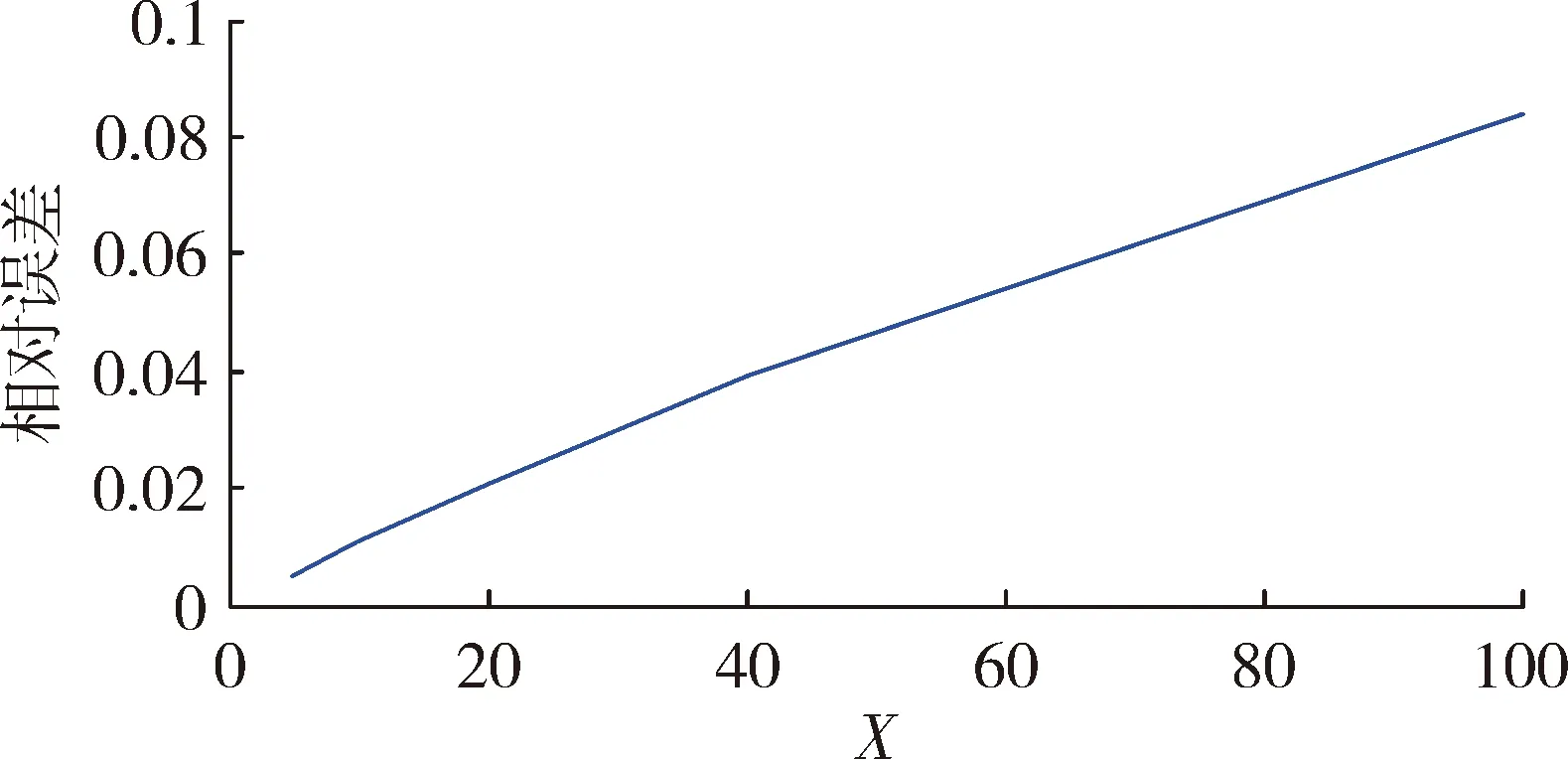
图7 X与相对误差关系图
由图7可以看出,X和误差成正比;由图8可以看出,X对加速比的影响在X很小时相对较大,随着X的增大,其对加速比的影响逐渐减小。结合图7、图8可知,当X取仿真步长的5~15倍时,具有较好的效果。
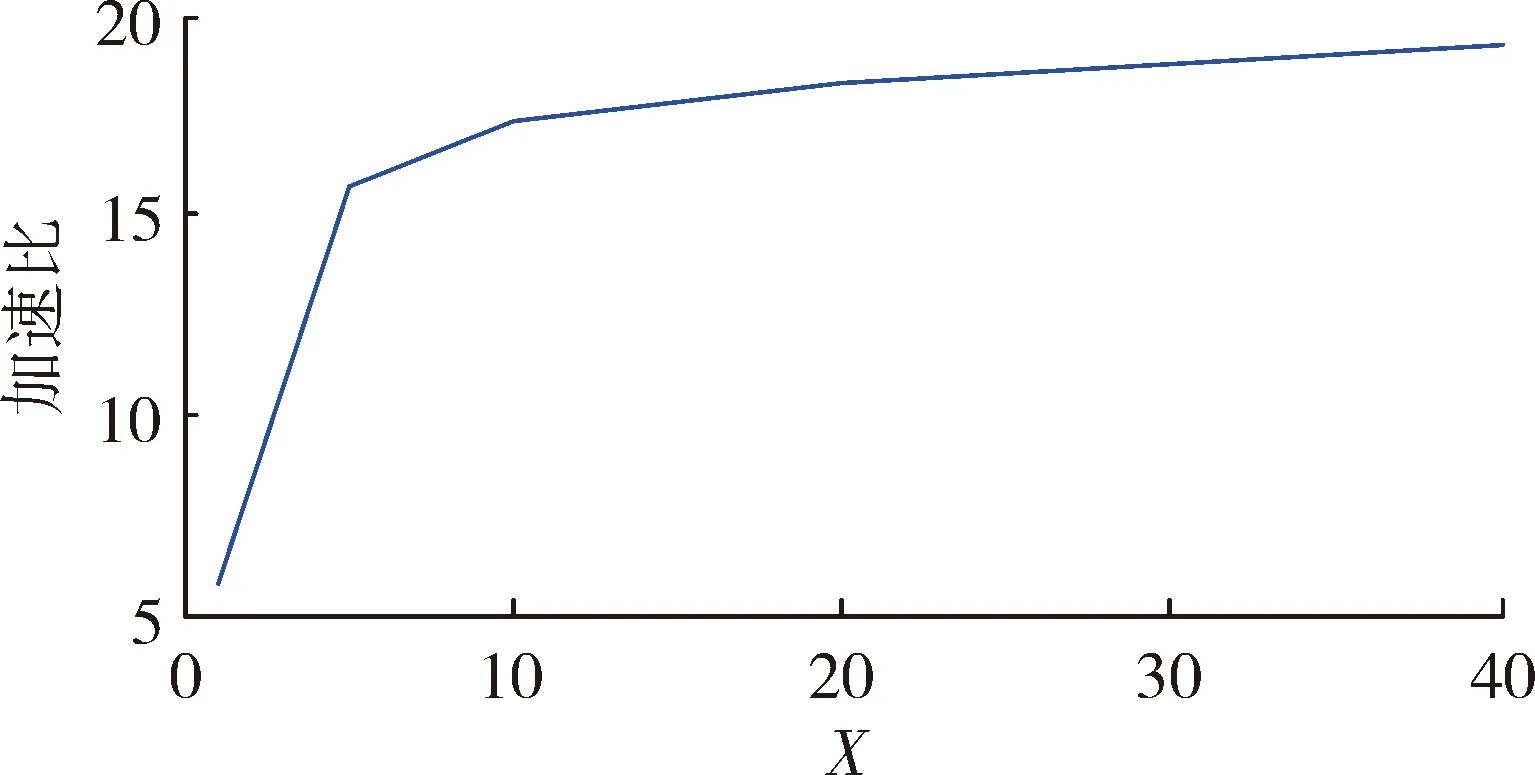
图8 X与加速比关系图
5 结论
从仿真结果可知,通信步长对求解误差以及求解效率有显著的影响,当通信步长取仿真步长的5~15倍时,相对误差仅为0.01~0.02,验证了该并行仿真方法的正确性;加速比达到15~20,验证了方法的高效性。图6体现出了GPU在大规模数值仿真中的优势,并且实验所用GPU性能较差,计算能力(compute capab-ility)仅为2.1,最新的GPU计算能力能够达到7.1,因此GPU在大规模仿真中有着广阔的应用前景。

