偏置比例导引律在空地作战中的应用

穆忠伟 吴剑 何诚 张哲

在现代空地作战中,精确制导武器对于取得战争胜利的主动权至关重要.它也是战场中敌我双方较量的关键武器,研究制导律性能尤为重要[1].关于制导律的研究大多数是以零化脱靶量、攻击角度约束、能量控制、法向过载控制等为重要的研究指标.经典的比例导引律在导弹的制导性能方面依然是占据重要地位.但是在约束攻击角度的性能上,偏置比例导引律要比其更具优势.

关于偏置型比例导引律方面的方法有很多的学者进行了研究.文献[2] 是以比例导引模型为基础,研究了偏置项作用时间、作用起止时间、期望落角和导航比等对偏置比例导引所构成的影响,推导出了偏置比例导引律的数学模型.文献[3]针对常用的比例导弹导引律在反导作战中的机动能力和效率的问题,提出了具备对目标垂直和水平机动跟踪能力的一种扩展的比例导引律.文献[4]针对导弹飞行过程中受到的外部扰动对前置角的变化有很大的影响,基于现有的分段迭代求解剩余飞行时间的方法进行了拓展,设计了满足相应的任意初始前置角和末端攻击角度约束的偏置比例导引律.文献[5]是基于比例导引律和末端攻击角度误差反馈,并对导弹飞行时间进行了精确设计,提出了一种不包括线性近似项的导引律.文献[6]中为了约束针对反坦克导弹命中的角度姿态,设计了一种考虑落角约束的制导律.文献[7]针对微型拦截器需要高精度的制导控制,研发了偏航及滚动优化姿态控制系统,设计了偏置比例导引律.文献[8]针对在大气层外拦截器进行直接的动能碰撞的方式进行目标毁伤,设计了发动机不具备变推力工作状态并适合轨控发动机的开关阈值的偏置比例制导律.近年来,关于非线性系统的有限时间稳定性收敛问题也得到了很多的研究[9-13],所以设计能够具备有限时间收敛特性的偏置比例导引律也是十分必要的.

本文主要针对空地作战中攻击静止目标和运动目标的约束攻击角度的问题,运用偏置比例制导律的优点,同时又具备一定的有限时间收敛的特性,再加上利用滑模变结构控制对外界的扰动及内部的参数摄动具有极强的自适应性和鲁棒性,将二者结合所设计的偏置比例导引律将对制导律性能的提高具有重要的意义,也提升了空对地导弹的末制导段的整体性能.

1 弹目相对运动关系

图1表示导弹M与地面目标T的几何关系,其中Oxy为惯性坐标系,M表示导弹,T表示目标,导弹速度V为恒定r为导弹与目标间的距离,a为垂直于导弹速度的法向加速度,θ 表示弹道倾角,η 为导弹速度V与弹目视线LOS 之间的夹角,q代表视线角.

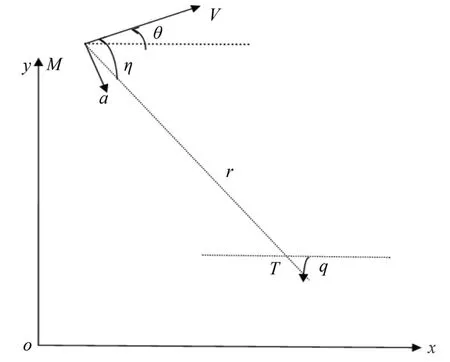
图1 导引几何关系

弹目相对运动方程为

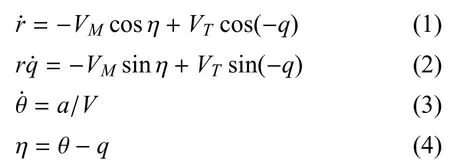
在导引的初始时刻t0时,r(t0) =r0,q(t0) =q0,θ(t0) = θ0,η(t0) = η0得出传统的比例导引法的关系式为

2 新型偏置比例导引律设计及有限收敛性证明

2.1 新型偏置比例导引律设计

导弹基本的偏置比例导引律具有如下的形式

其中,K≥2,x为待设计的偏置项.将式(3) 代入式(6)中并约掉两端的V可得

将式(7)两端在[t0t]上积分计算,可得

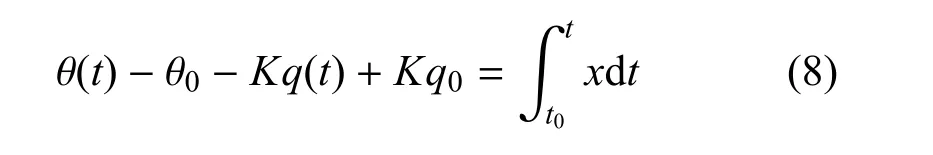
令tf为导弹击中目标的时刻,那么根据文献[12]有

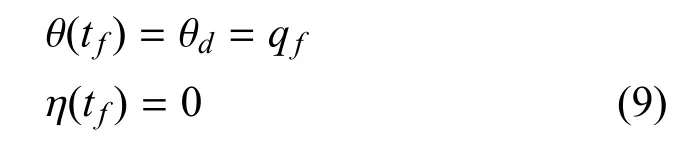
其中,θd为终端的攻击角度.将式(9)代入式(8)中,并将tf替换t可得

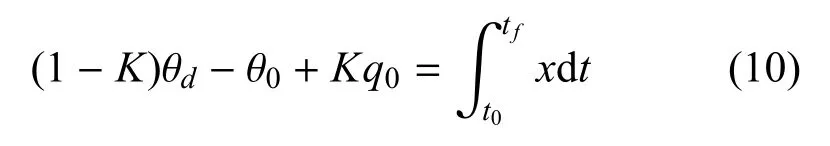
在t时刻,令并其代入式(10)可得

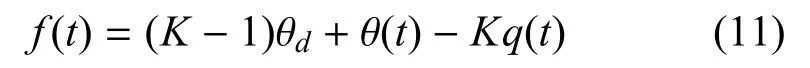
由式(11)可以得出t从t0到tf,f(t0)到f(tf)的变化为

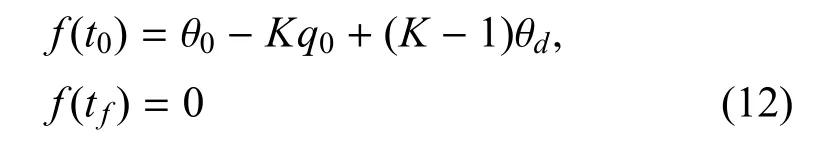
那么将偏置项问题转换为f(t)从f(t0)收敛到0的问题,这样就可以满足攻击角度的要求.

接下来结合滑模变结构控制,首先利用f(t) 收敛到0 的特性,设计一个滑模切换面,因此设计切换函数为

当系统进入滑模切换面后,f(t) 收敛到0,而合理的趋近律会使系统具有优良的动态品质.

采用具有自适应特点的指数趋近律[14],可以保证系统具有正常的动态品质.趋近律如下:

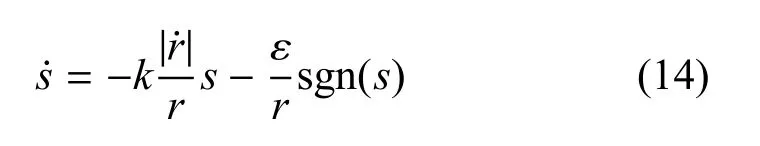
其中k＞0,ε ＞0.

将式(13)两端求导可得:

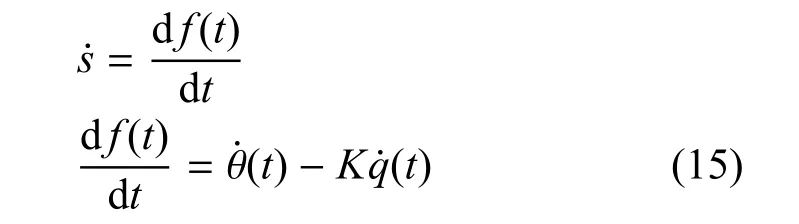
将式(14)与式(15)两端联立可得:

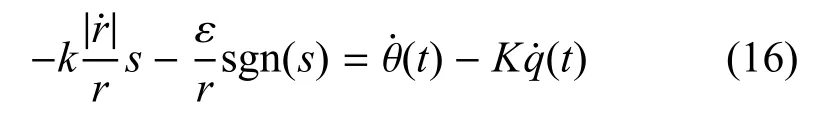
将式(3)及式(1)代入式(16)中可得:

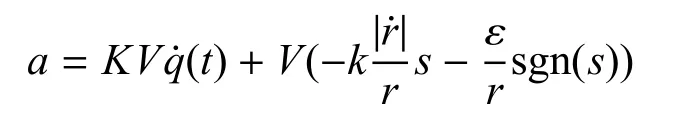
进一步得出:

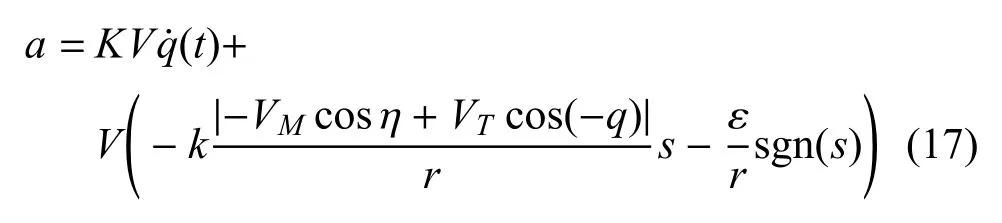
式(17) 所得结果是最终的新型的偏置比例制导律.

2.2 有限收敛性的证明

下面证明系统的趋近状态与滑动状态,首先证明其趋近阶段的状态,根据文献[15]选取Lyapunov函数Va=s2,对其两端求导数可得如下:

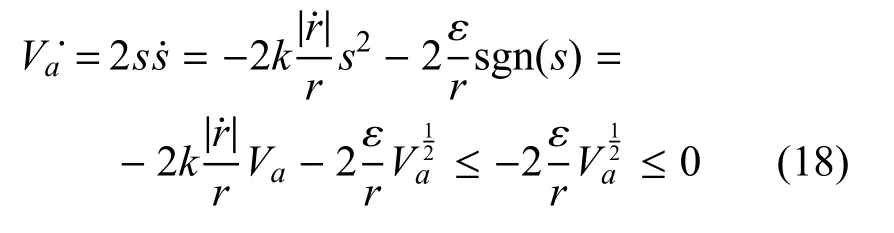
根据文献中的引理可得,系统可以在有限时间内收敛到滑模面.

接下来,对系统收敛到0 进行证明.选取Lapunov 函数Vb=f(t)2,对其两端进行求导可得如下:

接下来构造f(t)的动态如下:

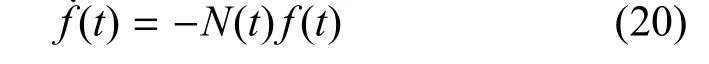
其中,N(t)＞0,选取即随着弹目距离越来越近,f(t)收敛的速度就越快,那么˙r< 0.cos η ＞0将N(t)代入式(20)中可得:

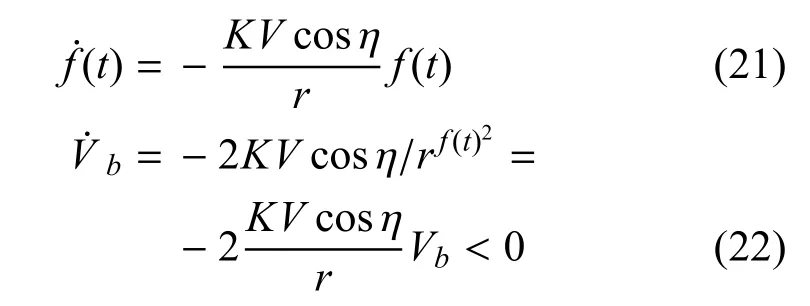
据文献[16]有限时间收敛的引理可知: 系统可以在有限时间内收敛到0.

3 仿真分析

3.1 导弹打击固定目标的仿真

导弹在制导的过程中,针对地面固定目标时,目标速度VT= 0,导弹的初始坐标位置为xm= 0,ym=4 000,初始弹道倾角为θm= 0,导弹的速度vm=260 m/s;目标的初始坐标位置为xt=4 800,yt=0,期望落角为-60°；制导参数取值:ε=0.01,K=5,k=3.本文将与传统的经典比例制导律进行比较如下:

其中,N=8,下面将本文提出的新型偏置比例导引律与传统比例制导律进行对比.

首先根据仿真结果可得,比例制导律和偏置比例制导律的制导时间分别是24.5 s、25.4 s,脱靶量分别为2.469 7 m、0.261 0 m.角度误差分别为43.915 4°和2.358 8°.偏置比例制导律的拦截时间要比比例导引律的拦截时间稍长些,根据图2可看出这是因为比例导引律的弹道曲线较低,而偏置制导律的弹道曲线较高.在实际的空地作战中,较高的弹道为提供更快的攻击速度及更大的毁伤效果带来很大的优势.脱靶量又小,具有更精准的制导效果.

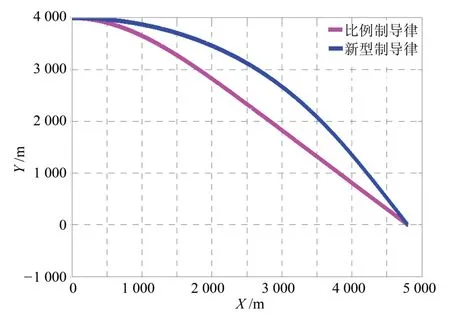
图2 两种制导律的弹道轨迹

根据图3可以得出,偏置比例导引律比比例导引律能更好地约束特定的角度攻击目标,角度误差还很小,以精准的角度命中敌方目标的特定位置,例如在空地作战中攻击地面目标的动力装置、弹药库所在的位置,能更准确地针对目标的特定部位进行毁伤,大大提高了导弹打击目标的灵活度.

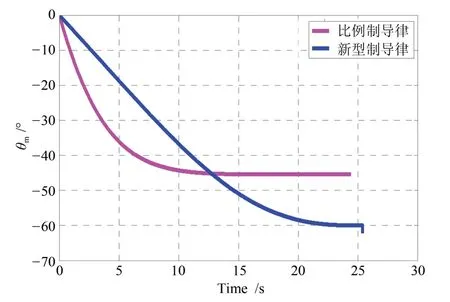
图3 两种制导律的弹道倾角曲线

根据图4可以得出,两者制导律的加速度曲线刚开始相差较大,而后两者都迅速较少直至向0 收敛.证明本文所提出的制导律性能更佳.

根据图5可以得出,偏置比例制导律的视线角最终趋于-60°,实现了弹道倾角与视线角最终趋于一致的结果以特定姿态攻击目标.而比例制导律却以很大的误差击中目标.并且图6中各自角速率都趋于0,证明都可以以一定的角度命中目标.

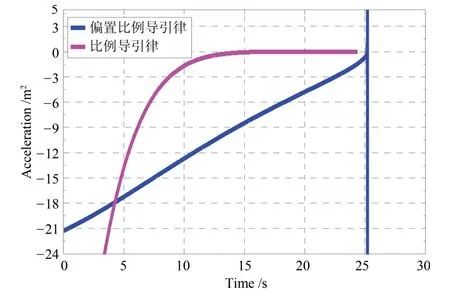
图4 两种制导律的加速度曲线

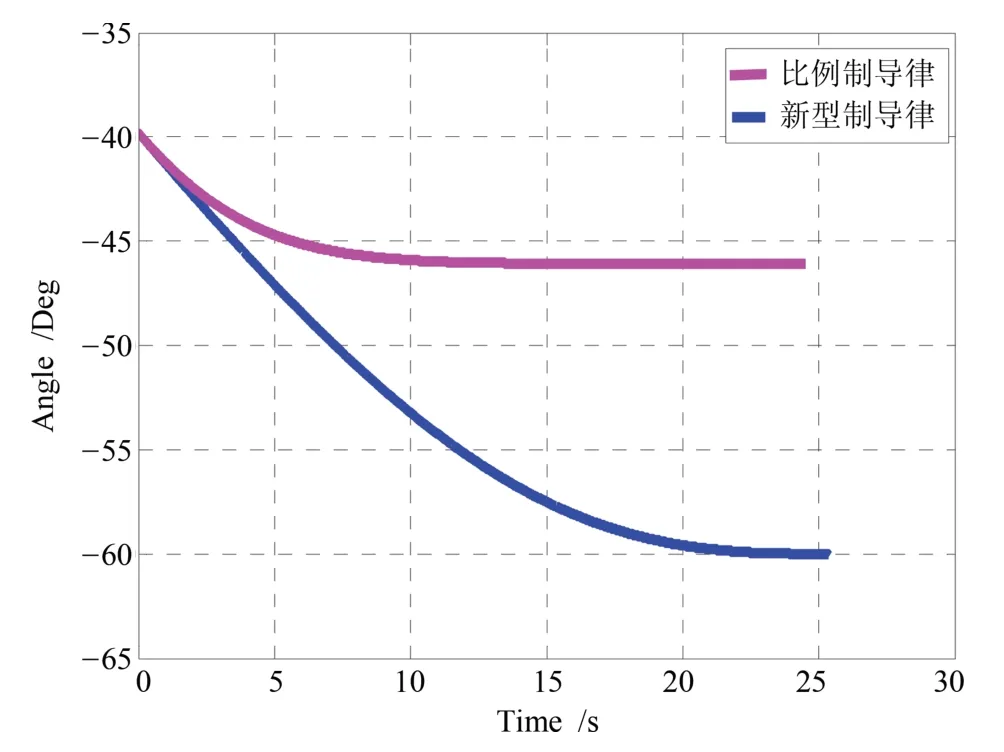
图5 视线角曲线

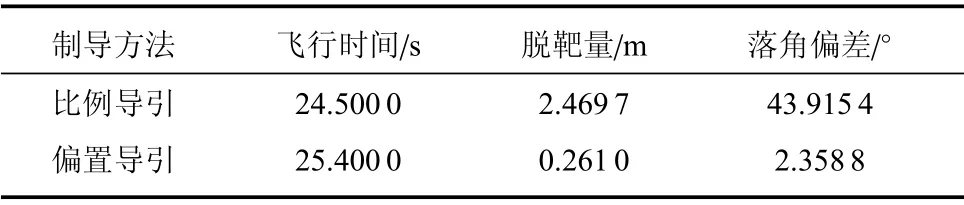
表1 两种导引律制导效果的比较

3.2 导弹打击运动目标的仿真

导弹在制导的过程中,导弹的初始坐标位置为xm= 0,ym= 4 000,初始弹道倾角为θm= 0,导弹的速度Vm= 260 m/s; 目标的初始坐标位置为xt=4 800,yt= 0,目标速度Vt= 150 m/s；期望落角为-30°；制导参数取值:ε=0.01,K=5,k=3.

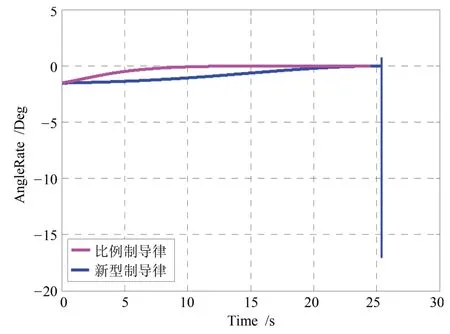
图6 视线角速度变化曲线

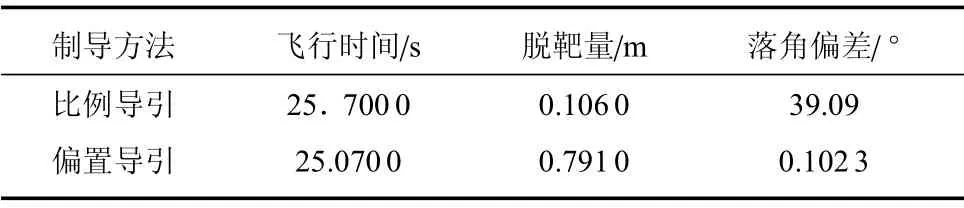
表2 两种导引律制导效果的比较

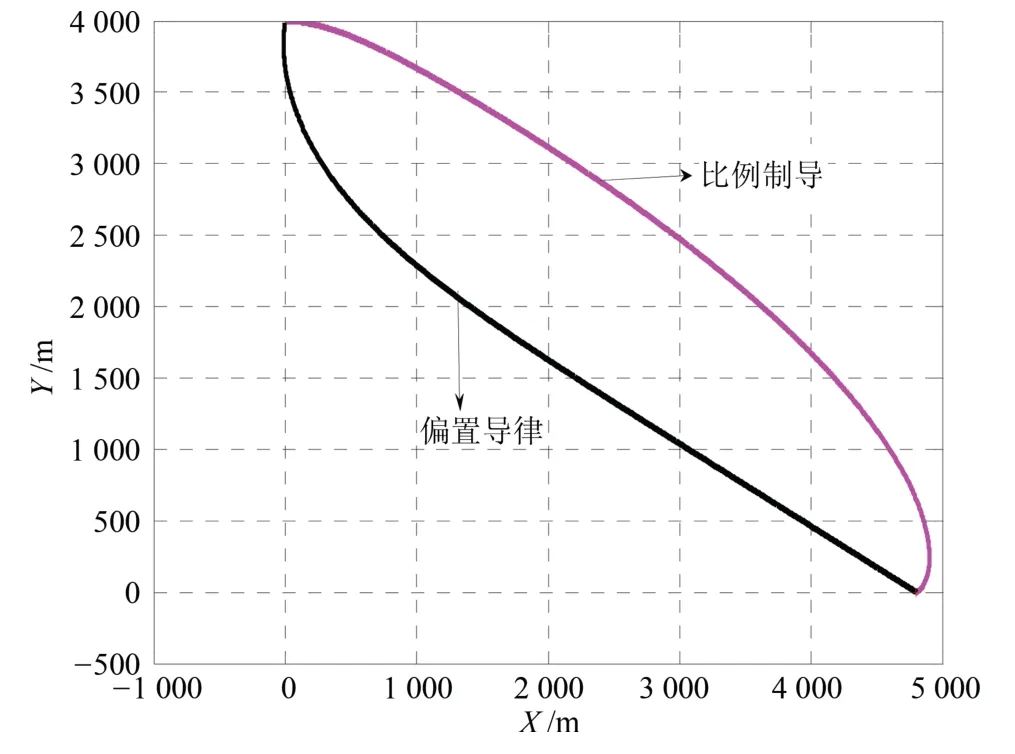
图7 弹道轨迹

结合表2和图7可知,偏置比例导引律使导弹的飞行时间要比比例导引的时间短,弹道低于后者的弹道；图9可知,偏置比例导引的弹道倾角趋于期望落角为-30°,而后者则落角偏差相差40°,所以从攻击落角看,偏置比例导引攻击运动目标的落角更佳.

由图8可知,偏置比例导引的过载曲线最终趋近于0,而后者的过载曲线大小先大、后小、再变大.最终趋于分散,相比性能,偏置比例导引使导弹末制导段的机动性能更高.

由图10可知,两者视线角速率最终都趋于零,而比例导引律趋于零后又分散,使导弹的脱靶量更大.

4 结论

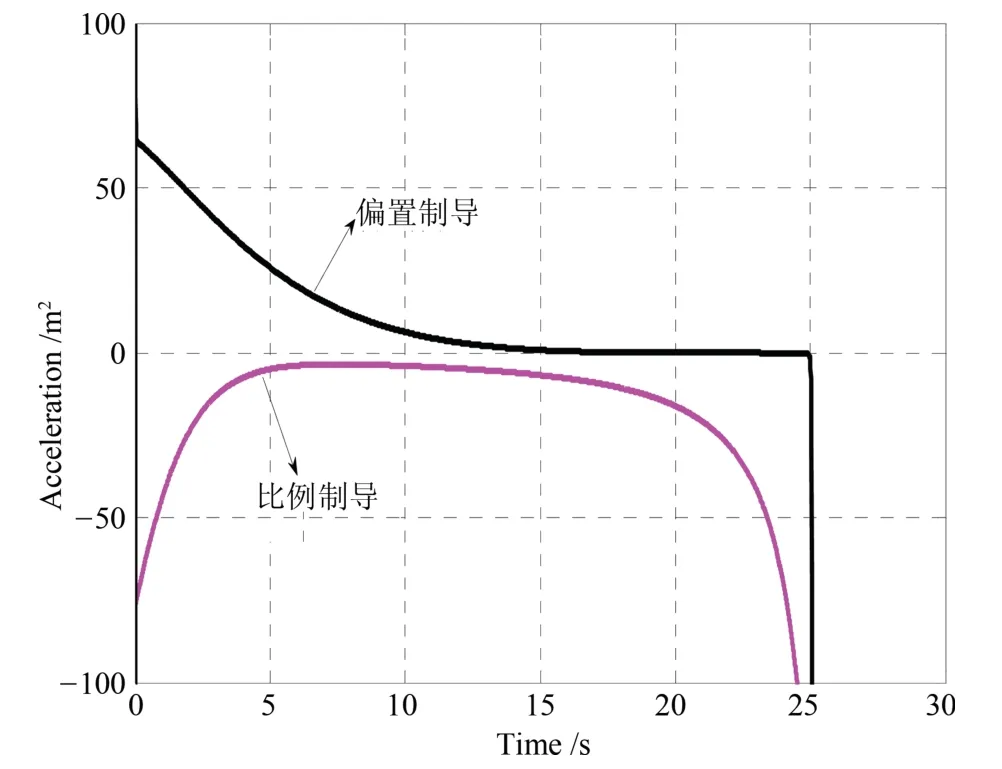
图8 过载曲线

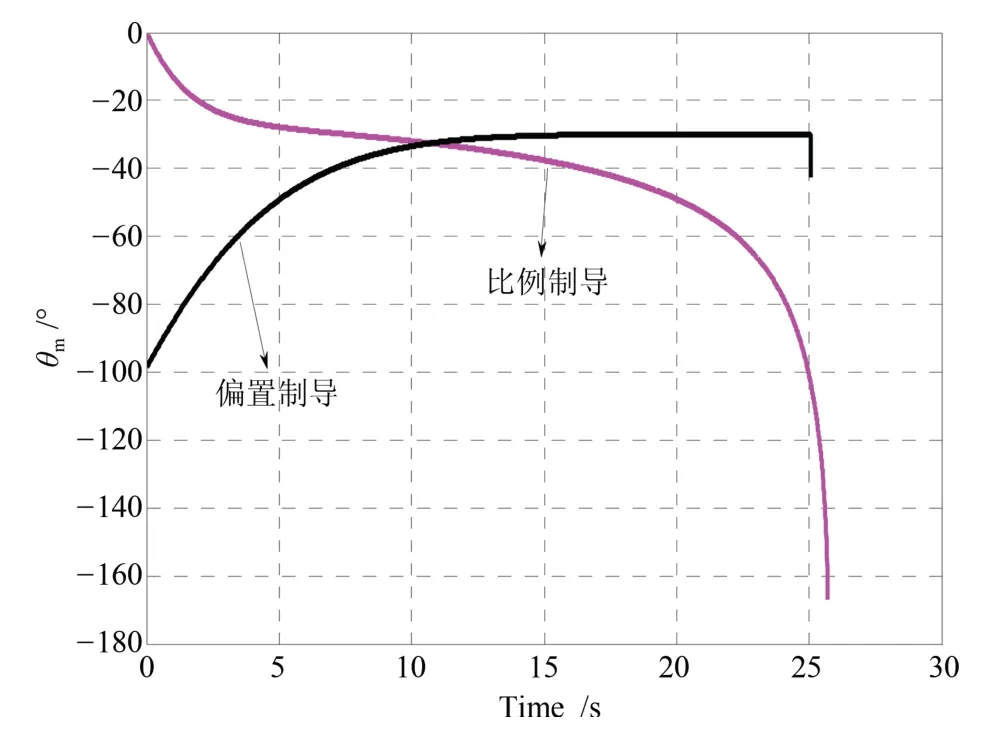
图9 弹道倾角

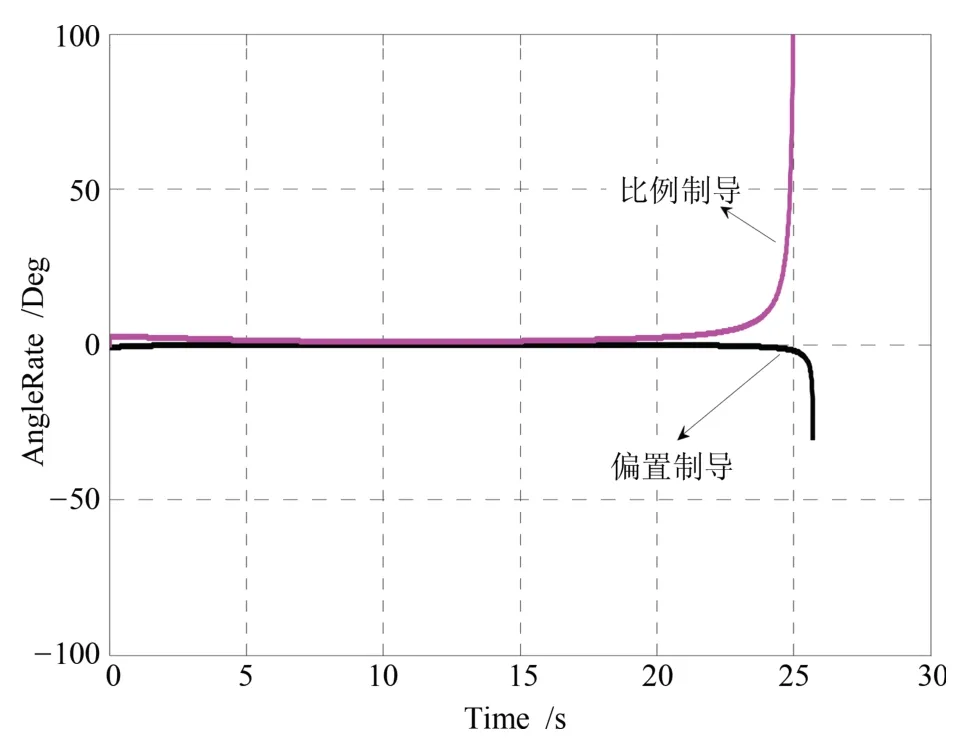
图10 视线角速率

针对在空地作战中导弹以一定的落角打击地面目标的问题,本文提出了一种偏置比例导引律.利用弹目之间的相对运动关系,基于积分换算的设计思想,通过结合滑模变结构理论使偏置比例公式中的偏置项对内及外具有自适应性.除此之外,该制导律能够保证导弹在末制导前期尽可能地充分利用导弹的机动能力,以使制导律尽快地收敛,那么在制导的末端,也能保证落角的约束.与传统的比例制导律相比,本文所研究的偏置比例制导律在制导精度及制导角度方面都更具优势.