基于贝叶斯网络的“低慢小”目标威胁评估方法

2019-12-26 01:38辛振芳黄魁华何晶晶贾彦翔邱旭阳

指挥与控制学报 2019年4期

辛振芳黄魁华何晶晶贾彦翔邱旭阳

威胁评估(Threat Assessment,TA)是以目标属性与状态推断以及态势评估为基础的高层信息融合技术,是指挥中心进行作战指挥决策的一个重要环节.“低慢小”(Low Slow Small,LSS) 目标主要是在低空慢速飞行的小型无人机或空浮器[1],其具备侦测难、管制难、治理难等特点.随着国内低空空域改革进程的加快以及通用航空器研制水平的不断提升,各类民用低空飞行器迅速发展,一方面对传统的防空作战带来新的挑战,另一方面给城市安防带来新的不确定性因素.近期报道的几例以无人机为代表的“低慢小”目标擅自闯入事件都给城市安防带来巨大困扰,严重影响人们生产生活.因此,亟需研究能够有效处理“低慢小”目标的防控系统,威胁评估作为“低慢小” 目标防控系统的基础性关键环节,直接影响“低慢小”目标防控方案的制定和防控效果.本文主要研究以无人机为代表的典型“低慢小”目标威胁评估方法.

在传统防空作战中,常用的目标威胁评估方法主要包括模糊集方法、层次分析法、灰色关联度分析、贝叶斯网络、逼近理想解的排序法、云模型理论方法或多种方法的合成等[2-5].目前针对“低慢小” 目标研究威胁评估的文献较少,主要使用AHP、TOPSIS 等方法进行评估.文献[6]针对“低慢小”目标,利用层次分析法推出层次结构,并建立威胁度评估指标体系,最后用实例验证了评估模型的有效性,但AHP 方法过度依赖指标体系和专家系统的支持,其主观性过强; 文献[1]中利用排序法求解规范决策矩阵时比较复杂,且由于权重设置方法的不同,权重具有一定的随意性;文献[7]以目标类型、速度、距离等6 个因素作为威胁评估因子,利用模糊集与信息熵和TOPSIS 算法相结合的方法进行排序的威胁评估,该方法只能推算出目标威胁的大小排序,并不能给出“低慢小”目标具体的威胁值.

实质上,针对“低慢小”目标进行威胁度评估时,需考虑很多的影响因素,其中包含定量因素,也包含定性因素.对“低慢小”目标进行威胁评估的关键环节是影响因素的选取与处理.本文综合分析影响目标威胁评估的定量因素和定性因素,同时考虑到威胁在时间上的连贯性,提出一种基于动态贝叶斯网络的“低慢小”目标威胁评估方法.

1 相关原理简介

1.1 贝叶斯网络

贝叶斯网络是一种概率图模型.是以概率推理为基础的数学模型,其在处理不完整性以及不确定性的问题上具有明显优势.贝叶斯网络的拓扑结构是一个有向无环图,主要包括网络结构与条件概率两部分,可用二元组S= 〈G,P〉表示,其中G代表网络结构,P代表条件概率.

1)G= 〈X,E〉,其中X= {X1,X2,··· ,Xn}是有向无环图的节点集合,E是有向边的集合,代表各节点之间的依赖关系.蕴含的条件独立假设为:图中各个节点Xi与其父节点的非Xi后代节点构成的任何节点子集均是条件独立的,若Pa(Xi)代表Xi的直接双亲节点,A(Xi) 代表非Xi后代节点组成的任何节点集,则

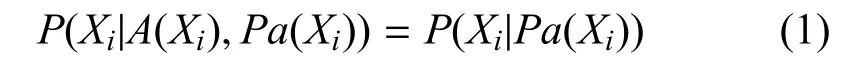
2)条件概率P是一种概率参数,其体现节点之间关联性的局部概率分布集,可用P(Xi|Pa(Xi)) 来刻画.条件概率传递了节点与其父节点之间的相互关系,若节点是根节点时,则其条件概率又叫做先验概率.

若贝叶斯网络的结构与条件概率表是明确的,则网络中所有节点(变量) 的联合概率密度可表达,并且可依据某些节点的取值或先验概率求解之后各节点的概率.在链规则上运用条件独立性,可得:

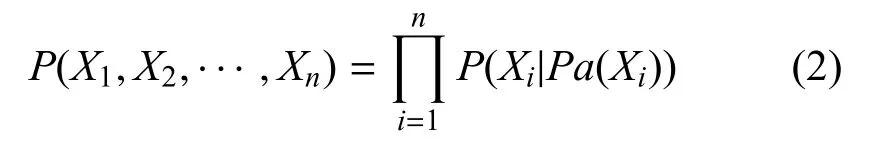
1.2 动态贝叶斯网络

动态贝叶斯网络是在静态贝叶斯网络的基础上,结合时间信息,并引入先后时间片的状态转移概率.此模型可将前一时间片对其后续事件的影响考虑在内,使模型的鲁棒性大大提高.动态贝叶斯网络需满足两个前提,即:

1)假设动态概率过程具有马尔科夫性,即:

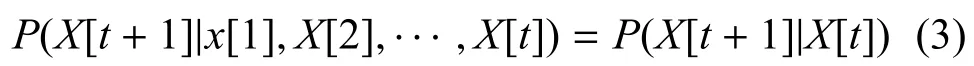
即t+1 时刻的状态概率仅仅与前一时刻有关,与其他时刻均无关.

2)假设相邻时间的条件概率在有限时间范围内都是平稳的,在任意t时刻,P(X[t+1]|X[t]) 均一致,则其是独立于时间的一个常量.

贝叶斯公式及其条件独立性是动态贝叶斯网络推理的理论依据,即

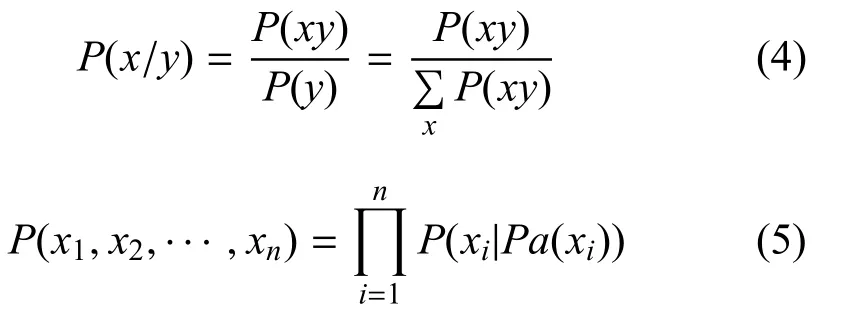
式中: (x1,x2,··· ,xn) 表示网络中的节点集合;P(x1,x2,··· ,xn) 表示网络中所有节点的联合分布;Pa(xi)是节点xi的父节点的集合.

在含有m个观测节点和n个隐藏节点的贝叶斯网络中,利用贝叶斯公式与条件独立假设,可推出[8]:

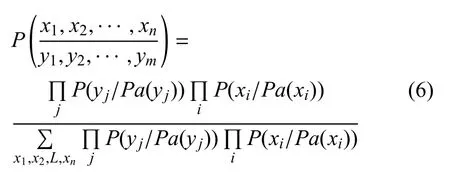
式中Pa(xi),Pa(yj)分别表示xi,yj的父节点的集合;i,j表示各自的节点数.

上述推理公式可延伸至有T个时间片的动态贝叶斯网络,若观测值仅含一种组合状态,此时观测值后隐藏变量的分布为:

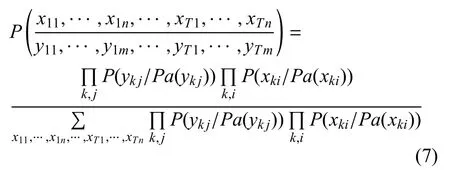
式中xki与yk j前面的下标代表第k个时间片,后面的下标各代表当前时间片下的第i个隐藏节点与j个观测节点,Pa(xki),Pa(yk j)各代表xki,yk j父节点的集合.

2 低慢小目标威胁评估框架

威胁评估的重要环节是影响因素的选取与处理,目前的威胁评估模型大部分从目标本身的特性出发,选取反映目标威胁的影响因素,忽略了我方对威胁目标处置能力的影响.本文综合文献[9-14]选取目标的速度、高度、距离、类型、作战能力、威胁意图以及我方处置能力作为“低慢小” 目标威胁评估影响因素,其中目标的速度、高度以及距离是可取得的连续性信息,归类于定量因素,目标的类型、作战能力、威胁意图以及我方的处置能力归类于定性因素.对于定量因素,首先根据各隶属函数求解相应的威胁值,其次基于AHP 方法确定各个因素的权值,然后计算定量因素的威胁值;对于定性因素,考虑到威胁在时间上具有连续性,构建动态贝叶斯网络拓扑,基于贝叶斯理论推出定性因素的威胁值; 最后将定量因素威胁值与定性因素威胁值结合计算出综合威胁值.

本文针对“低慢小” 目标进行威胁评估的步骤为:

步骤1.分析影响“低慢小”目标威胁评估的因素,将其分为定性因素和定量因素;针对定性因素构建相应的动态贝叶斯网络拓扑;

步骤2.输入当前时刻各定量因素的取值,通过各隶属函数求解定量威胁值THs;

步骤3.输入当前时刻各定性因素的取值,基于动态贝叶斯网络计算出定性威胁值THb;

步骤4.根据马尔科夫性获取下一时刻的威胁概率分布,在此基础上革新下一时刻的威胁先验概率分布;

步骤5.将定量因素与定性因素的威胁值相结合,求解综合威胁值并输出;

步骤6.检查是否含有下一时刻的观测数据,若有,则把下一时刻革新为当前时刻,返回步骤2; 否则,结束本流程.

图1为本文针对“低慢小”目标进行威胁评估的流程图,图2为“低慢小”目标的威胁评估的具体框架图.

2.1 定量因素的处理

通过雷达探测可以获取“低慢小”目标的速度、高度以及距离,本文利用隶属函数对定量因素进行处理.根据“低慢小”目标的自身运动特性以及专家实战经验,设定相应的隶属函数.

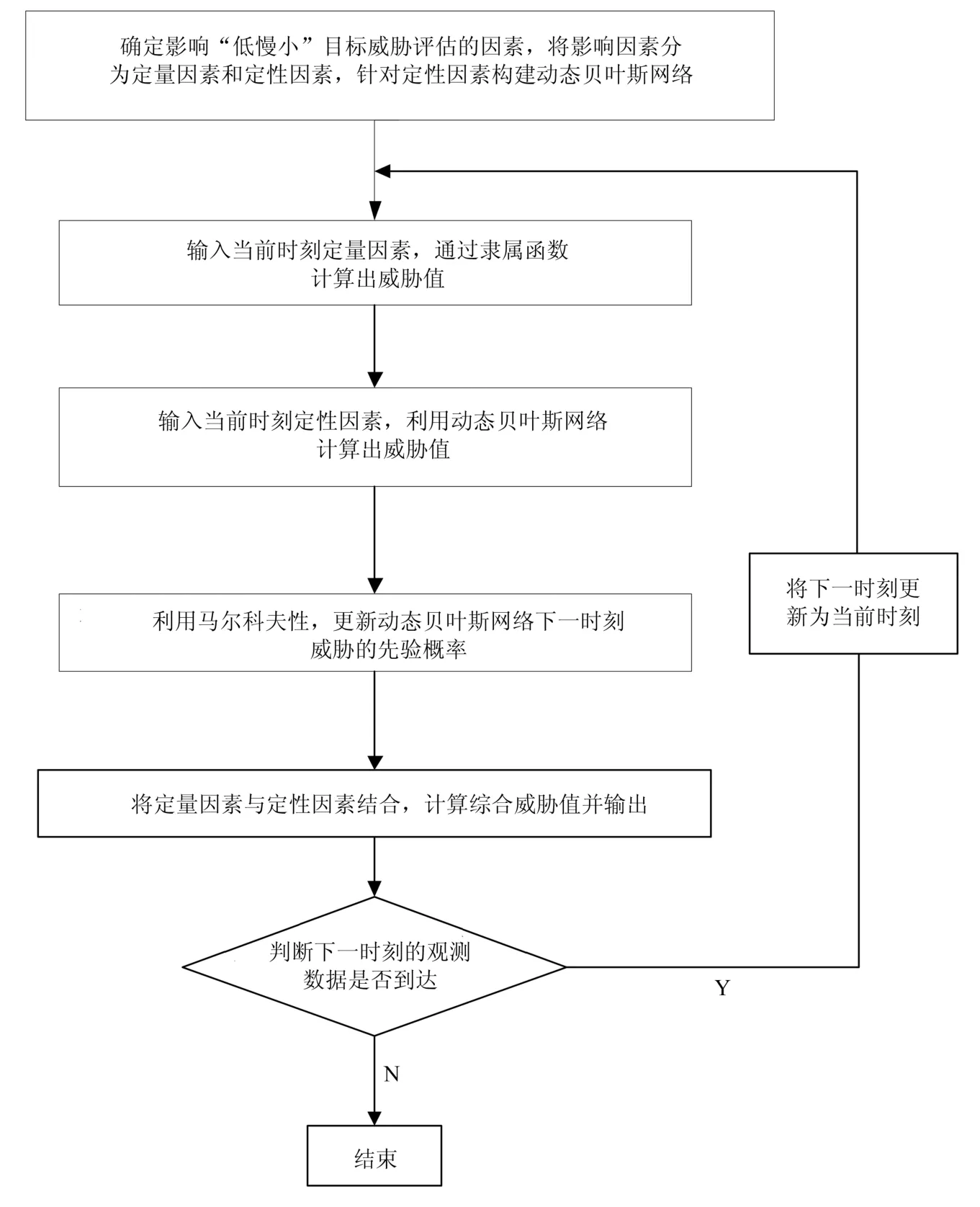
图1 “低慢小”目标威胁评估流程图

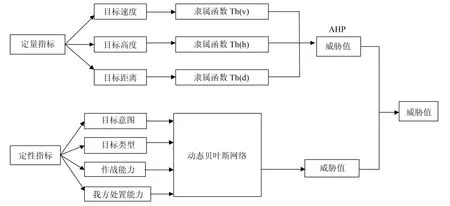
图2 “低慢小”目标的威胁评估框架

目标速度:理论上目标的飞行速度越大,则靠近我方越快,即威胁越大,因此,隶属函数呈上升型[15].本文设定: 当目标飞行速度大于30 m/s 时,目标的威胁为1,当飞行速度小于2 m/s 时,目标的威胁为0.2,则速度的隶属函数可表示为:

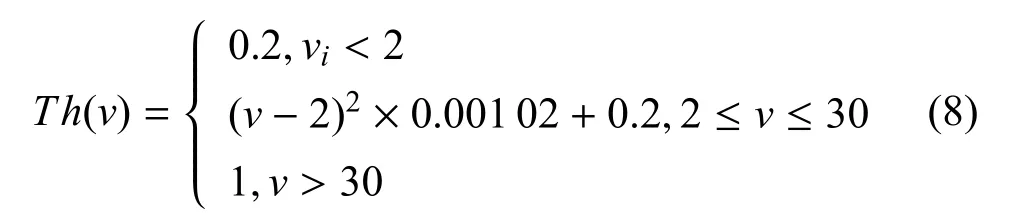
目标高度: 目标高度越低越容易躲避雷达的探测,因此,目标威胁随着高度的降低而增加,隶属函数呈下降型.本文设定: 目标的最小高度取值为50 m,则高度的隶属函数可表示为:

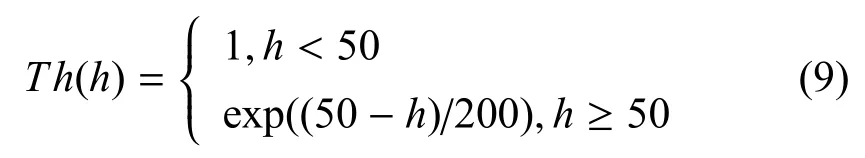
目标距离: 目标距离越小,靠近我方越快,则携带的威胁越大,因此,隶属函数呈下降型.本文设定:目标的最小距离取值为50 m,即距离的隶属函数为:

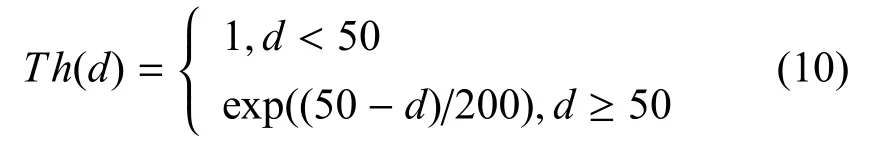
针对“低慢小”目标威胁评估的定量因素,首先利用隶属函数计算相应的威胁值,其次使用层次分析法确定各个定量因素的权重.AHP 方法确定权重的步骤如下[16]:

1)将定量因素两两作比较,设置判断矩阵;

2)根据判断矩阵求解被比较矩阵对威胁度的相对权重;

3) 在比较矩阵上做一致性检验,进而确定各定量因素的权重,即:

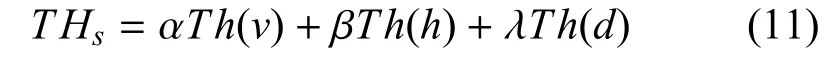
其中,对目标速度、高度以及距离设置的判断矩阵如表1所示:经过计算得到λmax= 3.009 2,其余特征值接近于零,则其最大特征值λmax＞ 3,因此,判断矩阵满足基本一致性.根据一致性的指标CI=(λmax-n)/(n-1) 和一致性比例CR=CI/RI,其中RI的值经查表可知为0.52,因此,CR= 0.009 < 0.1,即该判断矩阵近似满足一致性[17].最大特征值对应的归一化特征向量为u= [0.297 0 0.163 4 0.539 6],即为目标速度、目标高度以及目标距离的权重,因此,定量因素的威胁值为:

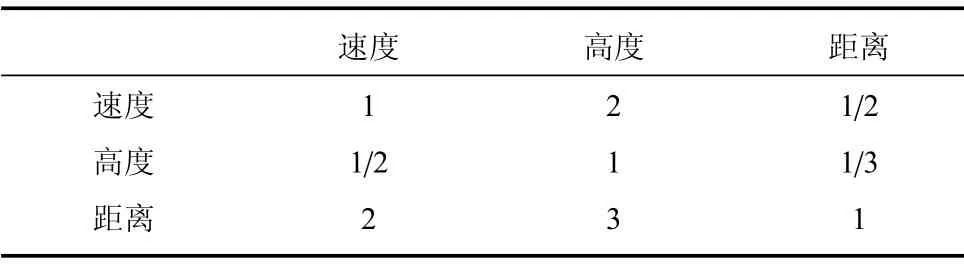
表1 定量因素判断矩阵

2.2 动态贝叶斯网络拓扑

动态贝叶斯网络是以时间为轴展开的一系列静态贝叶斯网络,且其网络结构及参数是一致的.前后两个时间片之间有弧连接,反映了变量之间的依赖关系,针对本文研究问题,基于马尔科夫性,利用威胁的状态转移矩阵根据时间的发展,持续地革新目标定性因素的威胁的先验概率分布,前后时间片可反映出威胁在时间上的连续性,因此,本文基于动态贝叶斯网络构建模型求解目标的威胁.

针对影响“低慢小” 目标威胁评估的定性因素,即目标作战能力、目标类型、目标威胁意图以及我方处置能力,建立动态贝叶斯网络拓扑.

1)利用专家知识和经验,构造针对“低慢小”目标进行威胁评估的动态贝叶斯网络结构[18],如图3所示.

网络节点包括: 可观测节点和隐藏节点,其中可观测节点包括目标类型、目标火力、目标机动性、目标航路捷径、目标进入角、目标电子干扰能力、我方反应时间以及我方拦截打击能力,隐藏节点包括: 我方处置能力、目标的作战能力、威胁意图以及威胁程度.动态贝叶斯网络含有两层推理结构,首先将目标的火力和机动性融合为目标的作战能力; 目标的航路捷径、进入角以及电子干扰能力融合为目标的威胁意图; 我方反应时间和拦截打击能力融合为我方处置能力; 其次将我方处置能力、目标的作战能力、威胁意图以及类型融合为威胁程度;

2)设置各网络节点内容:

威胁(TH):威胁分为高、较高、中、低;

目标作战能力(CE):作战能力分为强、中、弱;

目标类型(ID):目标类型分为固定翼、多旋翼;

目标威胁意图(IN):威胁意图分为攻击、侦查、恐怖、民用;

我方处置能力(DC):我方处置能力分为强、中、弱;

目标火力(IF):目标火力分为强、中、弱;

目标机动性(IM):目标机动性分为强、中、弱;

目标航路捷径(L):航路捷径分为范围内、边缘、范围内;

目标进入角(C):目标进入角分为进入、远离;

目标电子干扰能力(J): 电子干扰能力分为强、中、弱;

我方反应时间(T): 我方反应时间分为快、中、慢;

我方拦截能力(S): 我方拦截能力分为强、中、弱;

3)设置各网络节点的条件概率分布、先验概率分布以及威胁状态转移概率分布;

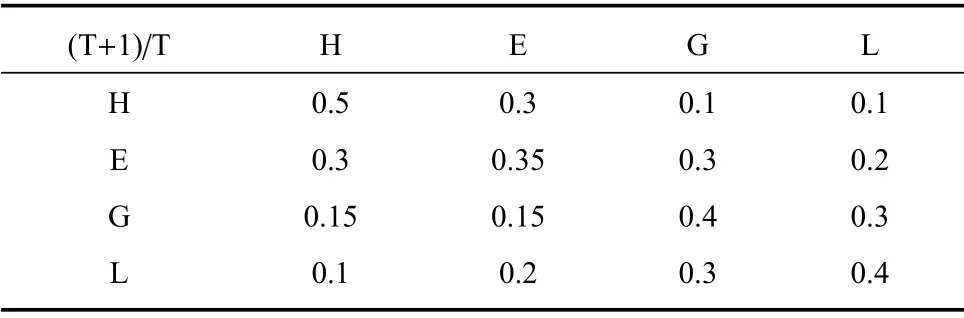
表2 动态贝叶斯网络威胁状态转移矩阵

条件概率矩阵一般是军事专家根据经验知识得出的,不排除主观影响.为提高样本的正确性,可对样本数据进行多次调试,适当调整矩阵中的数据.

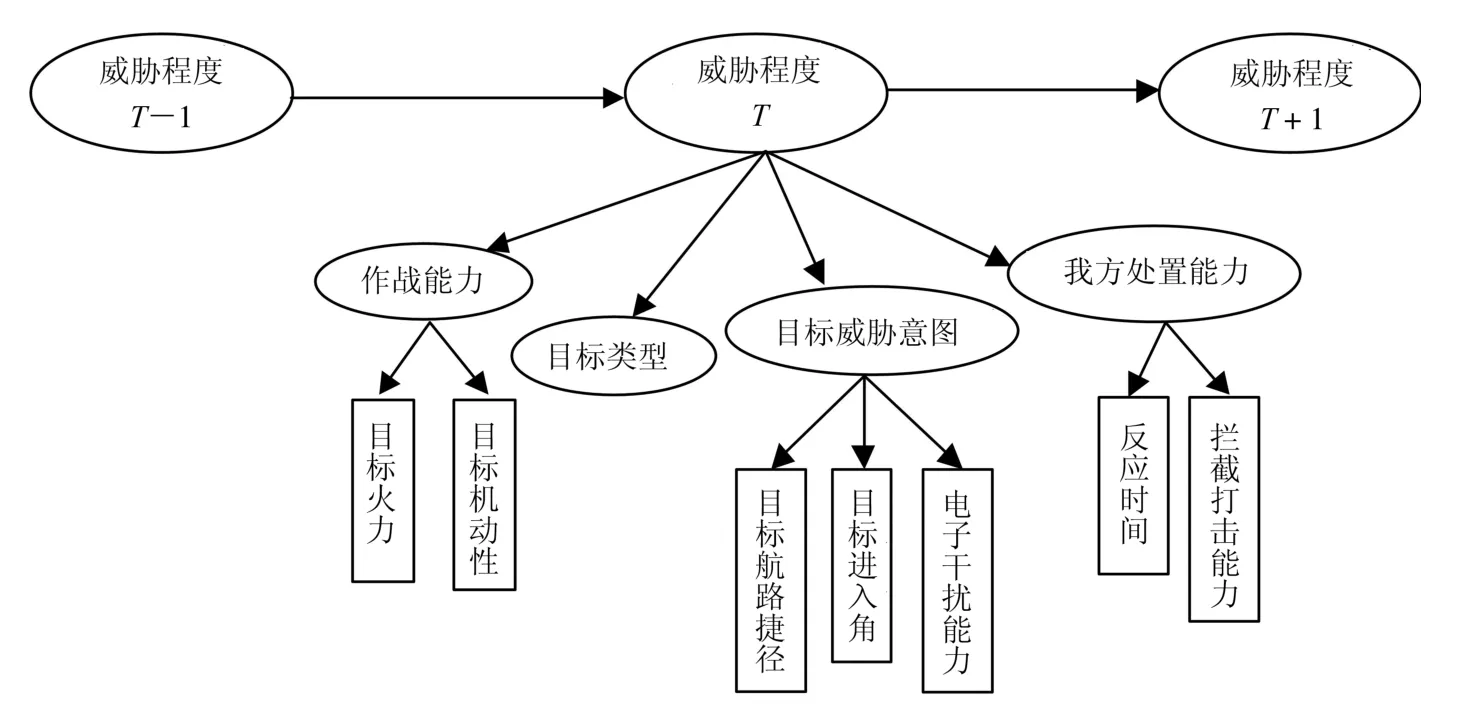
图3 动态贝叶斯网络拓扑

表3 威胁程度评估条件概率

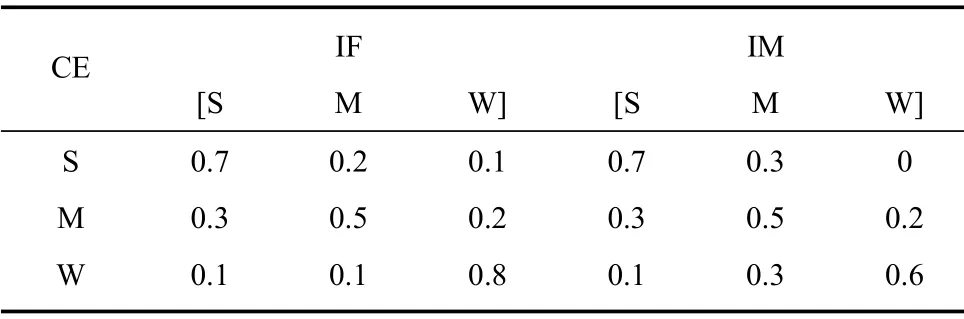
表4 目标的作战能力评估条件概率

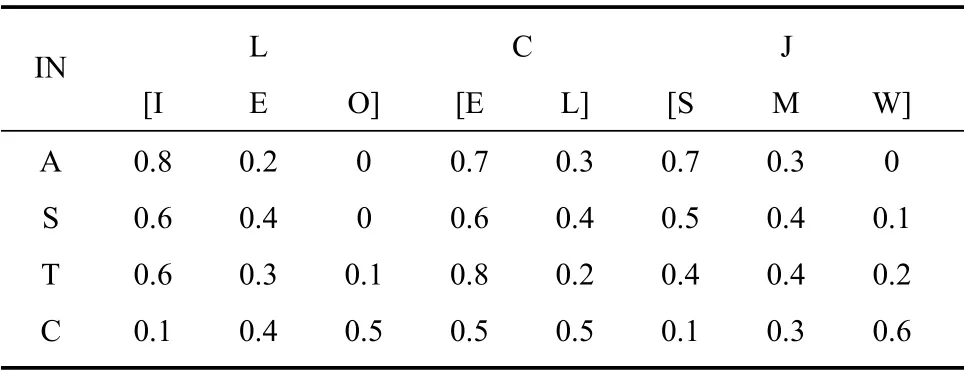
表5 目标威胁意图评估条件概率

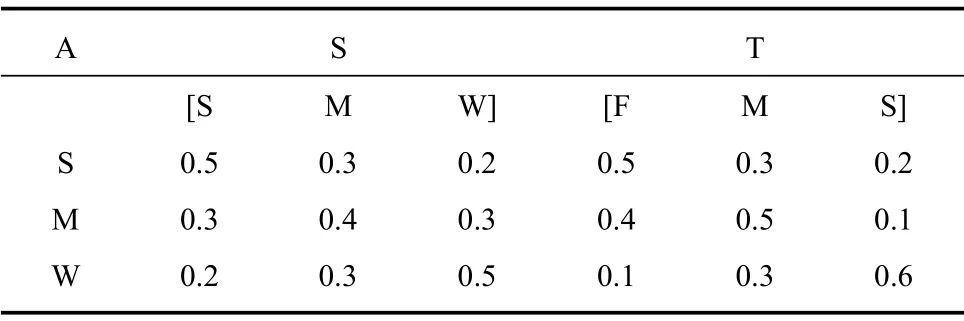
表6 我方处置能力评估条件概率

4)输入当前时刻动态贝叶斯网络的证据节点内容,利用联结树算法推出目标威胁的后验概率分布;

5) 利用当前时刻目标威胁的后验概率计算威胁值;

计算定性因素的威胁值THb.设定威胁度从高到低4 个等级的期望值分别为0.9、0.7、0.5、0.1,则THb为:

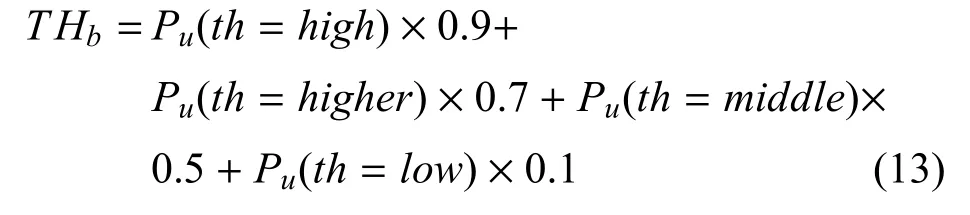
6) 基于马尔科夫性,利用状态转移矩阵革新下一时刻目标威胁的先验概率分布:

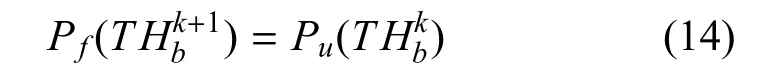
其中,下标f代表威胁的先验概率分布,下标u代表威胁的后验概率分布,k为当前时刻,k+1 为后一时刻.

结合定量因素与定性因素的威胁值,得到综合威胁值TH为:

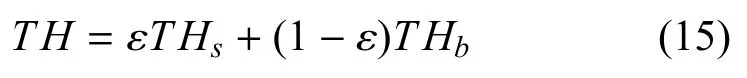
其中,ε 为权重因子,代表定量因素与定性因素之间的比重,ε 取值[0 1]区间,具体取值视实际情况而定.

3 仿真实验

假设某时间点我方雷达察觉到5 个反常的“低慢小”目标,不断对“低慢小”目标实施搜查与追踪,根据目标连续5 个时间片(时间间隔为5 s)的相关数据进行解析.运用Matlab R2014a 软件进行仿真实验,利用本文方法实现“低慢小” 目标的威胁估计,表7为5 个目标5 个时间片威胁的模糊概率,图4为5 个目标在各个时间片综合威胁值的变化趋势.

表7 5 个目标不同时刻威胁的模糊概率

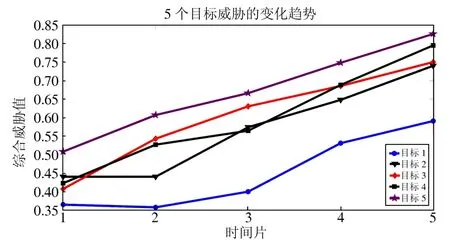
图4 “低慢小”目标的威胁变化趋势图

分析对比目标2 与目标3 的运动特征,开始时目标2 的距离、高度较近,因此,目标2 的威胁较大.随着时间的发展,目标2 一直匀速前进,而目标3 在飞行过程中加速,目标3 的威胁逐渐大于目标2 的威胁,本文评估结果与专家评估的结果一致.从仿真结果(图4) 可以清楚地看出,根据目标的运行信息,5 个目标在不同时间片综合威胁值的变化趋势,最终的目标综合威胁度排序为: 目标5 ＞目标4 ＞目标3 ＞目标2 ＞目标1,与专家经验评估结果相符,故本方法有效.

4 结论

本文提出一种“低慢小” 目标威胁评估的新方法,利用隶属函数和动态贝叶斯网络,对定量因素和定性因素并行评估,得到各个时刻目标的综合威胁值,此方法有效地考虑了威胁在时间上的连续性,具有良好的鲁棒性.且仿真验证结果与专家经验评估相符,因此,该方法具有实用性.