一个关于Fibonacci多项式及Fibonacci数的数列的注记

李小雪，陈国慧

(1.西安航空学院 理学院，西安 710077；2.海南师范大学 数学与统计学院，海口 571158)

0 引言

对任意正整数n≥0，著名的Fibonacci多项式Fn(x)由F0(x)=1，F1(x)=x及二阶线性递推式

Fn+1(x)=xFn(x)+Fn-1(x),n≥2

定义。

如果令x=1，那么Fn(1)=Fn+1是Fibonacci数，它的初值为F0=0，F1=1，且Fn+1=Fn+Fn-1，n≥1。

由于Fibonacci多项式Fn(x)及Fibonacci数Fn在数学的理论及应用方面都具有重要作用，因此，很多专家学者对它们的性质进行了研究，并得到了一系列重要结果[1-9]。

2018年，马元魁和张文鹏[10]研究了卷积和

的计算问题，这里的求和是对满足a1+a2+…+ah+1=n的h+1维非负整数数组(a1，a2，…，ah+1)求和。他们利用初等及组合的方法给出了关于Fn(x)的一个有意义的恒等式，即下面的结论：

设h是一个正整数，那么对任意整数n≥0，有恒等式

这里S(h,j)是由S(h,0)=0，S(h,h)=1 和S(h+1,i+1)=2·(2h-1-i)·S(h,i+1) +S(h,i)定义的二阶非线性递推序列，1≤i≤h-1是正整数。

本文作为文献[10]的一个注记，将对该文献中的结论进一步改进和完善。

1 主要结果

为了进一步理解S(h,i)的性质，本文列出了S(h,i)的一些值，如表1所示。

表1 S(h,i)的值

对于(2)式的应用，马元魁和张文鹏[10]证明了对任意素数p和满足0≤i≤p-1的整数i，有同余式

S(p,i)≡0 modp(p-1)。

经过大量的数据计算，可以发现序列S(h,i)具有简洁的精确表达式，也就是有下面的结论：

定理设h是一个正整数，对任意满足0≤i≤h的整数i，有恒等式

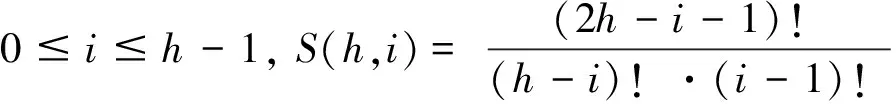
那么对h=k+1，当i=k时，由S(h,i)的定义，有S(k+1,k+1)=1，因此定理正确。如果0≤i≤k-1，那么由递推式

S(h+1,i+1)=2·(2k-1-i)·S(k,i+1)+S(k,i)

及推断假设(4)式，有

S(h+1,i+1)=2·(2h-1-i)·S(h,i+1)+S(h,i)

这意味着对h=k+1，定理成立。这就完成了定理的证明。

结合(3)式及文献[10]中的定理1，可推出下列结论：

推论1 设h是一个正整数，对满足0≤i≤h-1的任意整数i，有同余式

S(h,i)≡0 modh(h-1)。

推论2 对任意正整数h≥1，有恒等式

推论3 对任意正整数h≥1 ，有恒等式

2 结论

作为文献[10]的注记，本文研究了序列S(h,i)的性质，并得到了关于该序列的一个简洁精确的表达式。该结果不仅将S(h,i)复杂的递推式表达成简单的组合数从而便于计算，而且揭示了Fibonacci多项式和Fibonacci数的结构性质。也就是说，(2)式的卷积是由Fi(x)和一类组合数构成。此外，推论1进一步改进并推广了文献[10]的定理2，这意味着对于任意的正整数h，同余式成立且不受素数p的限制。

显然，本文结果可以进一步简化文献[10]的结论，文中的推论2和推论3就是对该文献相关结果的简化。