考虑自由液面波形的舰船水下辐射噪声计算方法
李 清,杨德庆,于 汉
(上海交通大学a.海洋工程国家重点实验室;b.高新船舶与深海开发装备协同创新中心,上海200240)
0 引 言
舰艇水下辐射噪声以声源级表征舰船的声隐蔽性,主要由机械噪声、螺旋桨噪声及水动力噪声构成[1]。舰艇机械噪声包括主机、辅机、泵系等引起的振动辐射噪声以及螺旋桨轴承力和表面力激励引起轴系振动和结构振动产生的辐射噪声,构成了舰艇水下辐射噪声的低频离散线谱,舰艇水下辐射噪声一般特指舰船机械噪声。
针对机械噪声,杨德庆等[2]利用有限元/边界元方法计算了某舰艇近场辐射噪声与自噪声特性;Zheng等[3]采用FEM-BEM 计算了柴油机激励导致的船体结构振动及其水下声辐射;付建等[4]计算了螺旋桨激振引起的船体结构振动与辐射噪声;李清等[5]归纳出求解舰船水下辐射噪声的两种模式及四种数值计算方法。以上文献中在求解水面舰船机械噪声时,均假定舰船与流体绝对静止,把自由液面边界作为平面计算舰艇水下声辐射,这种处理方式在国内工程实践中亦广泛多见。关于自由液面,黎胜等[6]研究了自由液面对脉动球辐射声功率和辐射指向性的影响;邹元杰等[7]探讨了自由液面和刚性壁面对结构振动与声辐射的影响;邹明松等[8]提出了带航速和考虑自由液面的声介质中三维水弹性结构声辐射计算方法,并以带航速的浸水弹性球壳为例,结合实验验证了算法的正确性。以上文献亦将自由液面作为绝对平面展开理论研究,指出自由液面对声辐射以及结构振动特性均有重要影响。然而,在目前公开发表的文献中,考虑自由液面形状的水面舰船水下辐射噪声计算方法的研究非常少。当求解航行状态下水面舰船辐射噪声时,自由液面处的声学边界已不再是平面,声学计算精度此时依赖于舰船航行的流场计算和声学边界处理。因此,探索考虑自由液面波形的水面舰船水下辐射噪声计算方法,探讨自由液面波形对辐射噪声计算精度的影响程度,对于提高水面舰船辐射噪声的计算精度具有参考价值。
本研究针对基于Wigley数学船型设计的某护卫舰,采用URANS方法基于SST k-ω湍流模型,数值计算Wigley 护卫舰在静水中匀速航行时的绕流流场,导出兴波波形作为声学计算时自由液面处的边界条件。应用声学有限元自动匹配层(FEM-AML)方法,采用声固耦合模式,建立了自由液面分别为波面与平面两种声学数值分析模型,计算了两种声学边界条件下的水下辐射噪声,比较了在两种声学模型下辐射声压分布、辐射声功率以及船体声振耦合响应,探讨了自由液面波形对水下辐射噪声计算精度的影响,为水下辐射噪声的精细化计算提供参考。
1 水面舰船流场及其水下辐射噪声计算理论
1.1 RANS方法与SST k-ω模型
采用基于RANS 控制方程的SST k-ω 湍流模型计算水面舰船绕流流场,SST k-ω 模型在近壁面处采用k-ω 模型,远处自由剪切流动采用k-ε模型,由于模型考虑了剪切力的影响,因此能够比较好地模拟强逆压梯度的流场。SST k-ω模型中湍流动能k,湍流耗散率ω及涡黏性系数νt满足下面方程[9]

式中,有效Reynolds数及湍流产生项Rω定义如下:

k和ω方程的源项sk和sω如下:
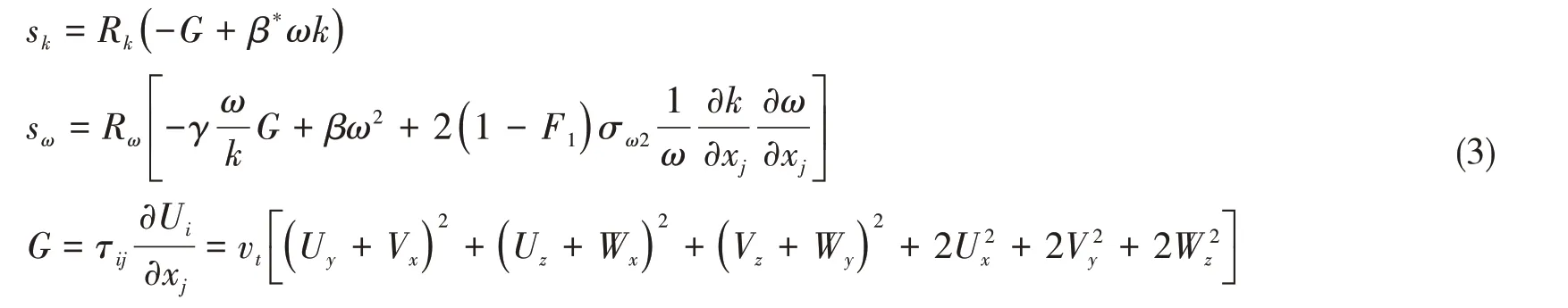
以上各式中:β*、β、σk、σω和γ 均为Blended k-ω/k-ε 模型常量,F1为混合函数,表达k-ω/k-ε 模型混合使用情况。
1.2 自由液面的数值模拟
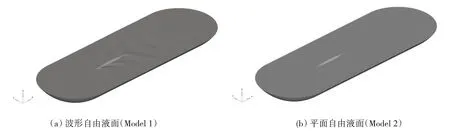
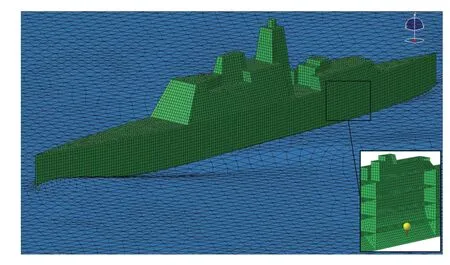
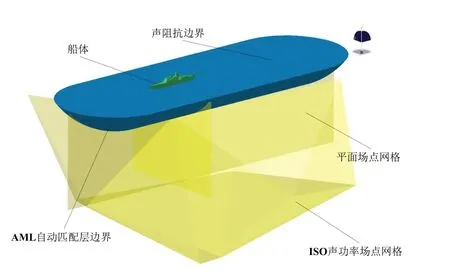
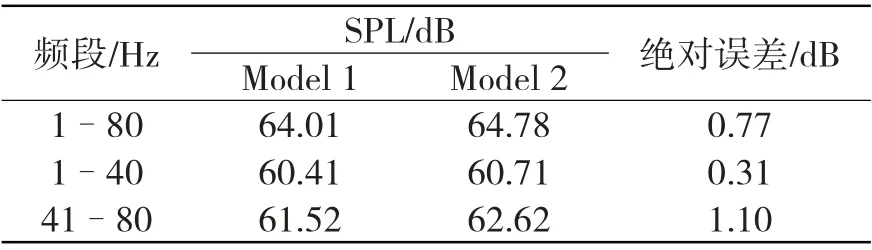
流体体积法VOF(Volume of Fluid)通过定义流体体积函数F 来标识每个网格单元状态,F 等于单元内流体体积与该单元体积之比。若F=1,则单元全部为制定相流所占据;若F=0,则单元为无制定相流体单元;若0 声波在两种媒质分界面处会发生反射与折射,其大小取决于两种媒质的特性阻抗。介质的声特性阻抗定义为介质中某点的有效声压与通过该点的有效质点速度的比值,亦可表示为介质密度ρa与声传播速度ca的乘积 基于声学有限元法计算舰船水下辐射噪声时,需在自由液面处赋空气特性阻抗以模拟阻抗边界条件[10]。 海水为重密度媒质,舰船振动辐射噪声计算必须考虑船体结构和流体的声振强耦合作用,结构和声学响应需同步耦合计算。理想均匀流中的声学基本方程为波动方程,对结构力场、声场进行离散推导得到的结构有限元耦合声学有限元的声固耦合动力学方程为[11] 本研究所用护卫舰简化模型在Wigley数学船型 基础上补充上层建筑及基本结构而成,式中各参数具体数值见表1。 表1 Wigley数学船型主要参数Tab.1 Main parameters of the Wigley hull Wigley 护卫舰结构模型主要包括6 层甲板、6 个纵舱壁等主要板结构,并由横梁、纵骨等主要梁结构加强,板结构用Shell单元模拟,梁结构用Beam 单元模拟。使数值船模固有特性符合实船模态分布,材料杨氏模量取E =40 MPa,密度ρs=7 850 kg/m3,泊松比μ = 0.3。Shell单元厚度均为10 mm,Beam 单元均为25×5 mm2矩形截面。护卫舰结构有限元模型(图1)网格尺寸需根据薄板横向振动弯曲波理论确定 式中:λs为薄板中弹性弯曲波波长,h 为最小板厚,fmax为分析频段最大频率。本研究计算频段为1-80 Hz,按上式计算得到λs=130.3 mm。为满足振动计算网格划分精度要求,本模型网格尺寸取为15 mm。本模型节点数为28 851,Shell 单元数为28 990,Beam 单元数为1 474。Wigley 护卫舰一阶水平弯曲振动、一阶垂向弯曲振动以及一阶扭转振动(图2)的固有频率分别为2.989 Hz、3.442 Hz和7.718 Hz。 图1 Wigley舰结构有限元模型Fig.1 Structural finite element model of theWigley frigate model 图2 Wigley舰总体振动特性Fig.2 Overall vibration characteristics of the Wigley frigate model 采用模态叠加法计算声振响应,参与计算模态基对应的最大频率一般取到计算频率的两倍以保证计算精度。故取本船前2 154 阶模态,第2 154 阶固有频率已经达到160 Hz(160.069 Hz),则本研究采用模态叠加法进行结构-声耦合计算,其结构模型可满足精度要求。以上计算了船体干模态,若采用船体湿模态进行声固耦合分析,将重复考虑结构与流体介质间的相互影响,计算结果会产生偏差[5]。 以Stoep[12]实验为参照,对Wigley 舰在静水中匀速航行的绕流流场进行数值模拟。本研究计算船模航行速度(来流速度)为1.627 m/s,船模航行弗劳德数Fr = 0.3,雷诺数Re = 5×106。 坐标系同图1,流体流向为x正向,重力方向为z负向。取入口距船艏0.75倍船长,出口距船艉2倍船长,侧面和底面距船体1倍船长,整个流场计算域为长方体;船体表面为无滑移边界条件,入口和出口分别为速度入口和压力出口边界,远场边界设置为对称边界条件(图3)。采用结构化网格(图4),船艏、船艉及水线面附近处流场变化较剧烈需进行局部加密,船体表面边界层根据y+= 30 计算得到的第一层网格厚度进行加密,网格总数约400万。 来流马赫数为0.1%,按不可压缩流动求解。基于压力求解器,时间类型为瞬态,采用URANS 方法,湍流模型为SST k-ω模型,多相流模型为VOF模型。当总阻力系数和自由面波高收敛,流场趋于稳定时,停止流场计算。由于舰船在静水中匀速航行兴波定常,在流场稳定后其自由液面不再变化,故取流体体积函数F = 0.5的等值面(自由液面)导出,作为后续声学计算的边界条件。 图3 Wigley船流场计算域及边界条件 Fig.3 Flow domain and boundary conditions of the Wigley hull 图4 Wigley船流场计算结构化网格划分Fig.4 Structured mesh for the flow domain of the Wigley hull 船舶总阻力Rt分为摩擦阻力Rf、兴波阻力Rw和粘压阻力Rpv,后两者共同构成剩余阻力Rr。本文计算得到的各项阻力系数与Stoep[12]实验结果(Fr = 0.3)比较见表2,其总阻力系数相对于实验值误差小于1%,剩余阻力系数与摩擦阻力系数与实验值也较接近;船体表面波高(图5)计算结果与Kajitani 等人[13]实验结果(Fr = 0.289)比较如图6,波高沿船长分布亦与实验值吻合良好。由于弗劳德数(Fr)不完全一致,波形主要于船艉处存在一定的差别。通过与相关实验对比,从阻力系数与自由面波高分布两方面验证了流场数值计算结果的可靠性。 表2 阻力系数与Stoep[12]实验结果比较Tab.2 Resistance coefficients compared with Stoep[12]experiment results 图5 XY平面自由液面波高分布 Fig.5 Free surface wave height distributions of the XY plane 图6 XZ平面船体表面波高与Kajitani等人[13]实验结果比较Fig.6 Hull surface wave height of the XZ plane compared with Kajitani,et al[13]experiment results 求解舰船水下辐射机械噪声时普遍假定舰船与流体均为静止,把自由液面边界视作不考虑波形的平面[5]。实际情况是航行中船体浸润区域时刻变化,自由液面处的声学边界应当考虑波面形状。因此,求解非定常流动中的舰船辐射噪声,其计算精度一定与自由液面流场形状和声学边界处理方法有关。当需要严格考虑自由液面波形时,因通过反对称平面构建自由液面的声学边界元法[10]已经失效,必须采用声学有限元法。为探索考虑自由液面波形的水面舰船水下辐射噪声计算方法,本研究建立的自由液面边界分别为波面和平面的两种(图7)声学数值模型,采用声学有限元自动匹配层(FEM–AML)方法计算Wigley舰水下辐射噪声,并探讨自由液面波形对辐射噪声计算精度的影响。 图7 Wigley舰两种自由液面声学几何模型Fig.7 Two Acoustic free surface geometry models of the Wigley frigate Wigley 舰水下辐射机械噪声计算频段为1-80 Hz,采用声固耦合分析模式[5]。设定声学有限元环境,为细致描述自由液面波形分布特征,声学单元特征长度取0.1 m,总单元数约为230 万。声学单元模拟海水,密度ρa=1 025 kg/m3,声波传播速度ca=1 480 m/s。根据声波理论,80 Hz 声波波长λa=ca/fmax=18.5 m,声学单元尺度远满足计算频段最小波长内至少有6个单元的精度要求。图8为声固耦合水下辐射噪声计算模型。在船体机舱板架处施加垂向激振力Fz=1 N(图9),导入2.1节中船体干模态,船体湿表面(图8)为结构-声学耦合面,取频段内结构模态阻尼系数为1%,进行结构-声耦合同步计算远场声辐射。平面自由液面模型与上述类似。 在自由液面对应的网格处设置阻抗边界条件,赋空气特性阻抗Zp=416.5 kg/(m2·s),声场中表征远场边界的表面赋AML 声吸收边界条件(图10)。根据护卫舰主尺度,建立水下长17.25 m、深5 m 的平面场点以观测辐射声压分布,同时设置标准声功率球面场点以评估远场辐射噪声。平面自由液面模型亦与上述类似处理。 图8 Wigley舰水下辐射噪声声固耦合计算模型Fig.8 The vibro-acoustic model of the Wigley frigate for underwater radiated noise 图9 机械噪声激振力加载 Fig.9 The excited force for mechanical noise 图10 声学边界条件与场点设置Fig.10 Acousticboundaryconditionsandthefieldpointsetting 本研究计算了Wigley舰低频1-80 Hz的机械噪声声功率谱级,并通过平面场点观测水下辐射噪声分布及指向特性(图11)。船体机舱底部板架激振力激起对应频率点附近的船体模态,并导致船体结构振动,船体外板产生振动响应。依赖于速度连续边界条件,船体结构浸水外板向流体质点传递振动能量,船体由舰艏至舰艉一并向水下辐射声波,而能量大部分还是集中在舰艇机舱附近,艇体可视为线声源,流体亦产生声振耦合反作用影响船体结构振动,辐射噪声远场声压基本上随辐射半径增大而逐渐递减。采用自由液面分别为波面和平面的声场模型求解的声场分布特征以及辐射声压最值(Ref.1 μPa),均存在一定程度上的差异。 图11 Wigley舰机械噪声辐射声压分布(50 Hz)Fig.11 Radiated sound pressure distribution for mechanical noise of the Wigley frigate(50 Hz) 图12 为Wigley 舰声振耦合位移频率响应,两种声学模型对结构振动响应亦有一定程度上的影响。图13 为机械噪声远场辐射声功率谱级(Ref.1×10-12W)。根据图13 和表3 可知,两种自由液面声学模型计算所得辐射声功率频谱与其总声功率级均存在差异,两种模型的计算偏差为0.77 dB(约0.8 dB)。其主要原因是对于波形曲面与绝对平面两种自由液面模型,边界几何形状的不同导致了声辐射边界条件不同,结构-声耦合面(舰船湿表面)的几何形状亦有差异,从而使计算结果产生差别。表3 分别计算了1-40 Hz 及41-80 Hz两个频段内总辐射声级,两种模型绝对误差分别为0.31 dB 和1.10 dB,且随频率的增加而增大。图13亦表明,两种声学模型声功率线谱在较低频段基本吻合,而随着频率增大偏差愈明显。 综上,两种自由液面声学模型计算效率与计算规模基本相当,严格考虑波形的自由液面声学模型计算精度更高,且更加逼近真实物理环境。声学模型建模精度对机械噪声存在一定程度的影响,其影响程度随频率的增加而增大,自由液面为平面的声学模型的计算结果偏大。 表3 两种声学模型合成声功率级对比Tab.3 Comparison on overall SPLs of two vibroacoustic models 图12 声振耦合船体结构位移频率响应(50 Hz)Fig.12 Vibroacoustic displacement responses of the frigate structure(50 Hz) 根据以上结论可以推测,若计算水面舰船水动力噪声,自由液面波形对水动力噪声的影响程度应大于机械噪声。其原因在于:计算水动力噪声时,除了两种声学模型自由液面处边界条件、结构-声耦合面几何形状的差异,实际上船体浸润区域的不同亦会导致从流场映射到声学网格上的脉动压力(声压激励)存在较大差别,甚至后者可能对最终结果起主导作用;且水动力噪声是全频段连续噪声谱,中高频的声学计算更需要精确的声学计算模型。另一方面,自由液面波形对计算精度的影响程度因船型而异,影响程度的大小需具体船型具体分析,本研究中Wigley 数学船模瘦长且流线型规则,兴波现象并不明显,因而两种声学模型计算差别并不算大(0.8 dB);且对于实际工程水面舰船的水下辐射噪声计算,实船与模型间亦存在尺度效应,不可因本文研究结果之间的偏差较小而忽视自由液面波形对水面舰船水下辐射噪声的实际影响,而应根据实际工程对计算精度的要求选择合适的计算方法。最后,本研究模拟匀速航行水面舰船的静水兴波,流场稳定后自由液面不再随时间变化(定常),故可直接采用文中声场建模方法;而在模拟真实船舶航行时亦会存在随机波浪、变航向、变航速等非定常因素,此时可同样采用本文方法,将流场中各时刻对应的自由液面波形导出,分别建模计算各个指定时刻的水下辐射声场,或者进一步探索时域的声学计算模型。 以某Wigley舰为算例,综合探索了考虑自由液面波形的水面舰船水下辐射噪声的计算方法,探讨了自由液面波形对舰船水下辐射噪声计算精度的影响,为提高水面舰船辐射噪声计算水平提供参考与建议。研究得到以下结论: (1)严格考虑波形的自由液面声学模型计算精度更高,自由液面波形对舰船水下辐射噪声有一定程度上的影响,其影响程度随频率的增大而增加,自由液面为平面的声学模型的计算结果偏大。 (2)本研究数值模拟了舰船静水兴波匀速绕流的定常流场,自由液面波形是稳定的;若求解舰船在波浪中航行的非定常流场中的水下辐射噪声,自由液面波形及船体浸水表面时刻变化,可针对不同时刻的自由液面形状,分别建模计算水下辐射声场,或进一步探索水面舰船时域水下声辐射的计算模型与方法。 (3)采用基于URANS方法的SST k-ω湍流模型计算自由液面波形与实验吻合良好;但若求解舰船水动力噪声,由于固体壁面的偶极子声源的大小和分布特性决定其外部辐射声场的强弱及其分布规律,而URANS 方法针对舰船航行时的流动分离与尾涡计算存在明显不足,此时必须采用LES 湍流模型,亟待后续探讨。 (4)采用本文提出的计算方法可准确有效地预测舰船在航行时的水下辐射噪声。后续可深入探究舰船在不同航速下,波浪的特征波高、波长等因素对其辐射噪声的影响规律。

1.3 声固耦合有限元方程

2 Wigley型护卫舰及其航行流场数值计算
2.1 Wigley型护卫舰结构与振动模型
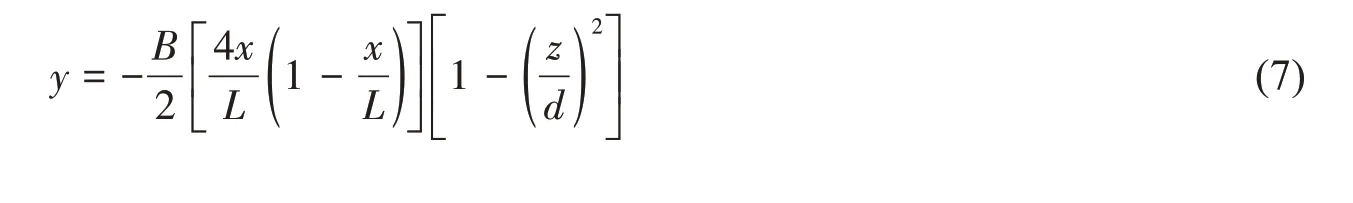




2.2 Wigley型护卫舰静水航行绕流流场数值计算



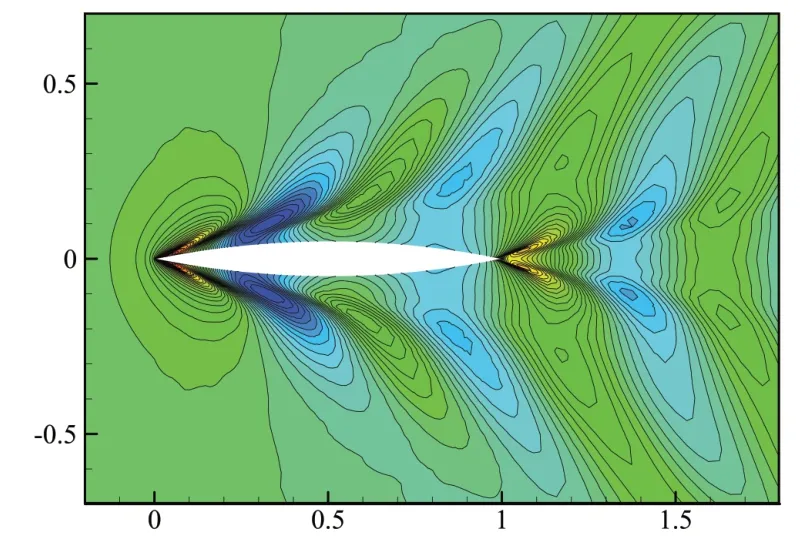
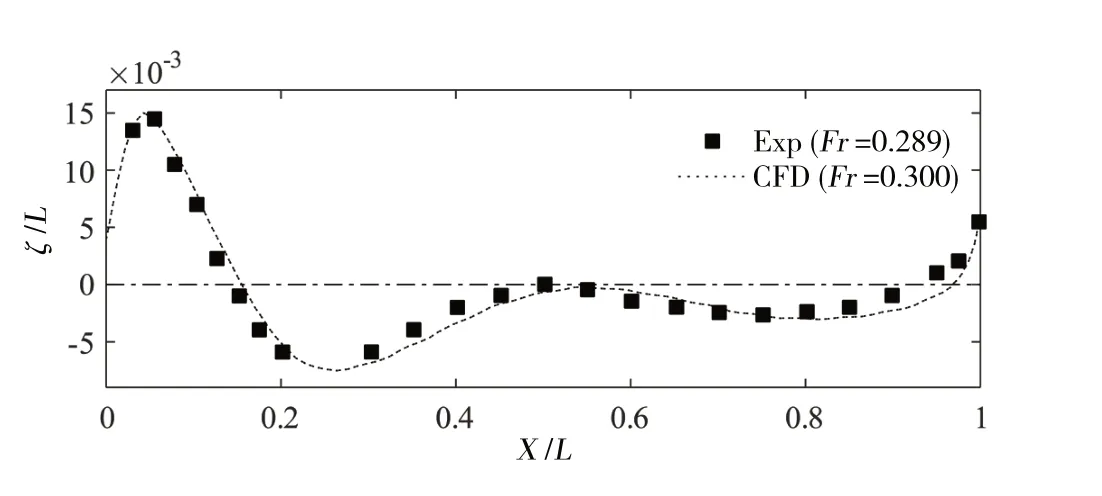
3 考虑自由液面波形的Wigley型护卫舰声学计算方法

4 Wigley护卫舰水下辐射噪声计算结果分析


5 结 论

