基于OpenFOAM 的无转角和有转角楔形体舱段入水砰击载荷数值模拟研究
骆寒冰,杨 宇,谢 芃,季红叶
(天津大学a.水利工程仿真与安全国家重点实验室;b.船舶与海洋工程系,天津300072)
0 引 言
合理预报船首砰击载荷关系船体结构安全,是船舶结构设计者及研究人员重点关注的问题之一。砰击是个非常复杂的水动力现象,涉及到波浪形状、船体表面几何形状、船波相对运动、空气层和水弹性等等[1]。由于该问题的复杂性,数值预报时通常要做许多假设和简化。船首砰击载荷的预报方法,通常可以分为两大类:一是基于耐波性方法模拟船舶在波浪中的运动,得到船波相对运动,再预报所感兴趣位置的砰击压力载荷响应;二是把所感兴趣的位置简化成二维剖面或者三维舱段结构,再开展入水砰击载荷预报研究。前者侧重于工程应用,目的是得到设计砰击压力,后者侧重于机理研究,预报砰击压力的时空分布特性,本文研究属于后者。
随着计算机技术的发展,显式有限元技术开始应用于入水砰击载荷预报。骆寒冰等[2]采用LSDYNA 商业软件对二维剖面开展了入水砰击数值模拟研究,预报结果得到了模型试验的验证,尽管采用了并行算法,但还是存在计算效率较低的不足。鉴于OpenFOAM[3]软件的开源性,二次开发功能强大,近年来,逐渐开始被应用于船舶与海洋工程水动力领域。罗天等[4]基于OpenFOAM 开发的数值求解器naoe-FOAM-SJTU,模拟了船模的横摇运动。李裕龙等[5]数值模拟了液舱液体的晃荡现象。不过,国内采用OpenFOAM软件预报砰击载荷的少见,国际上已经开始这方面的尝试。Vesselin等[6]针对二维楔形体非对称入水砰击问题,采用OpenFOAM预报了砰击压力及其液面变化历程。Andrea等[7]针对某三维简化结构开展了入水砰击数值模拟,预报结果与采用PIV技术测试的试验液面升高和PIV重构压力分布结果进行了对比。
本文主要针对楔形体舱段入水试验模型,采用OpenFOAM 软件,开发了基于两相流求解器Inter⁃DyMFOAM 数值模拟结构入水砰击的程序包,开展入水砰击数值模拟工作。无转角、有转角工况分别指的是结构对称、非对称垂直入水情况,用一个模型可以得到不同斜升角情况下的结果。数值模拟的砰击载荷结果与模型试验结果进行了对比分析,讨论了算法的计算效率以及计算精度。本文研究的主要目的是为今后预报三维复杂结构砰击载荷问题提供合理可靠的程序算法。
1 OpenFOAM 软件算法
OpenFOAM 是基于C++按照面向对象编写开发的开源软件包。本文自主开发实现了基于两相流求解器InterDyMFOAM计算楔形体砰击载荷的程序,其核心代码主要是基于有限体积法求解粘性不可压N-S方程系统,使用VOF方法对自由液面进行捕捉,预报砰击动压力载荷。基于不可压缩流体N-S方程的气液两相流模型基本控制方程如下:
连续性方程

动量方程

流体体积函数的输运方程

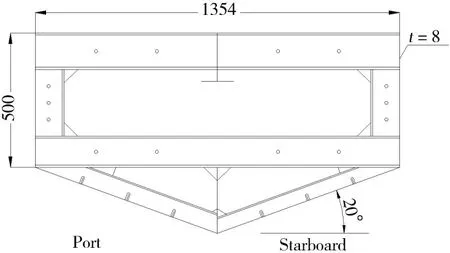
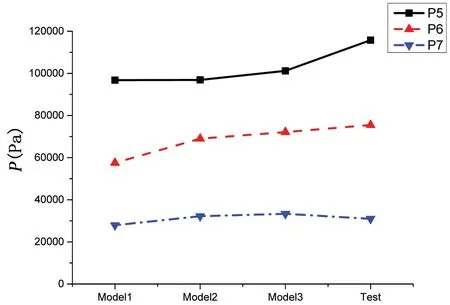
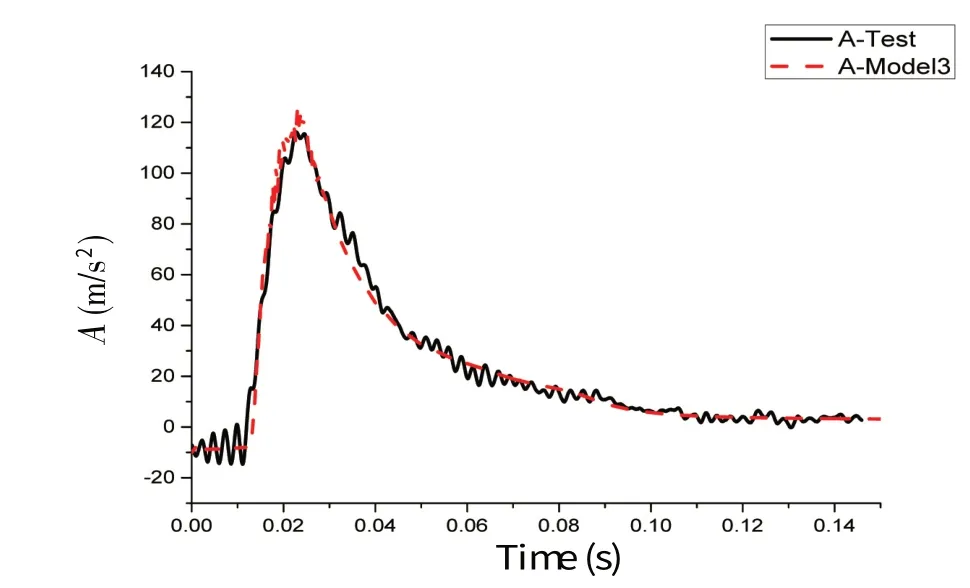
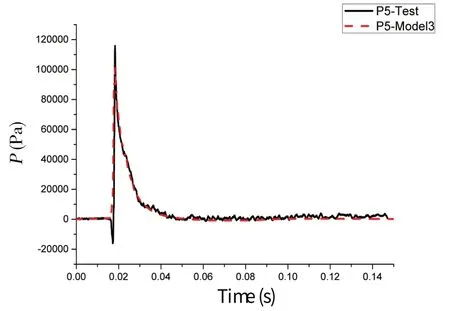
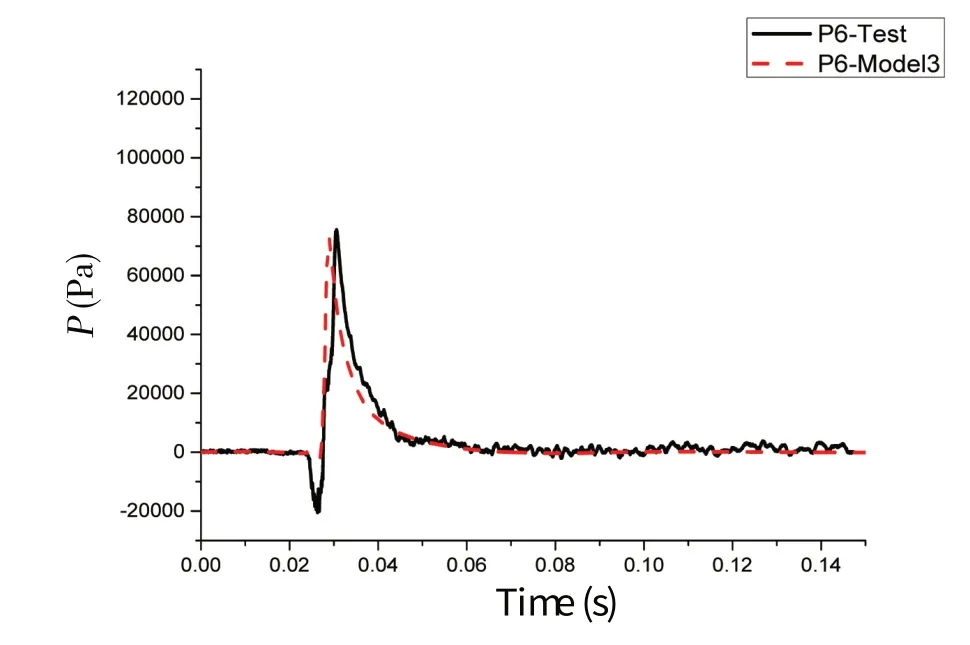
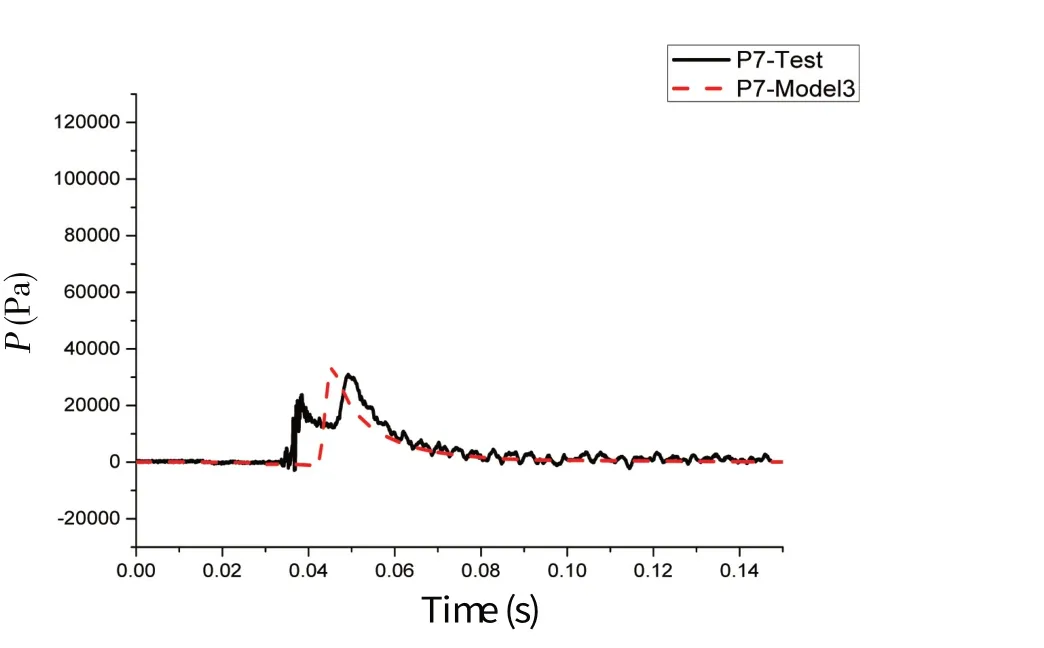
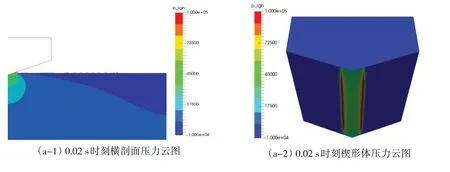
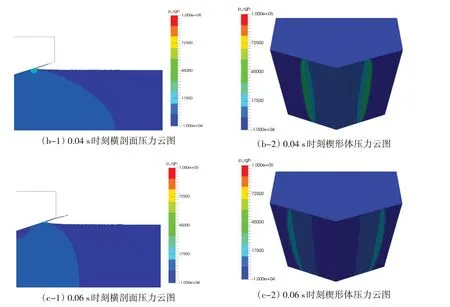
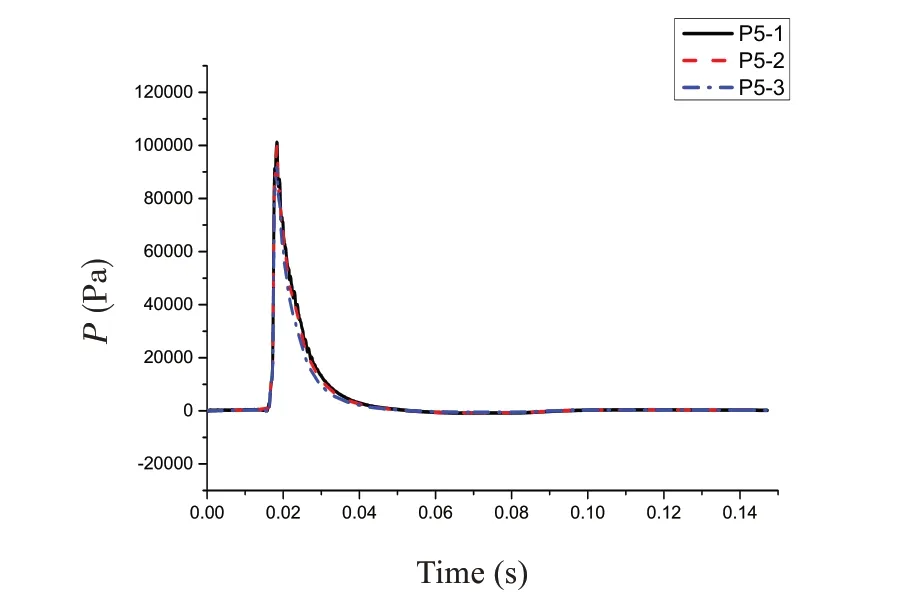
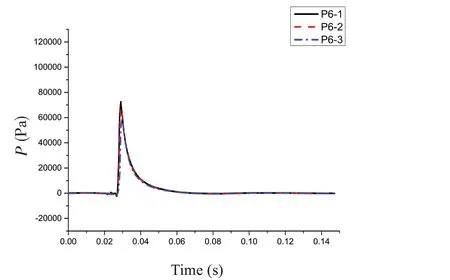
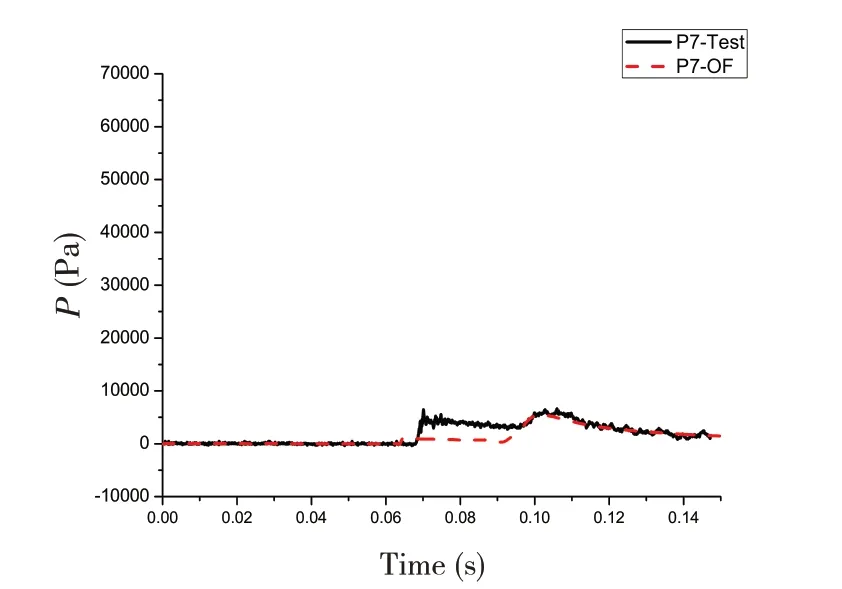
式中,ρ 为密度,U 为流速矢量,t 为时间,p 为压力,μ 是动力粘性系数,F 为体积力,包括重力和表面张力的作用;C 为流体体积函数,C=0 表示单元内的物质为空气;当C=1 表示单元内的物质为水;0 关于控制方程求解的离散格式,求解时间项使用欧拉法,梯度项使用高斯线性法,拉普拉斯项使用高斯线性修正法,插值格式使用线性法。离散方程中求解液面时使用3次修正迭代,动压力采用高次有限元方程的高效AMG 法求解,并利用对角不完全Cholesky 方法光顺,使用PIMPLE 算法控制压力与速度的耦合计算。湍流模型采用RAS雷诺时均模型中的k-ω SST湍流模型。 由于楔形体入水砰击整个过程物体在运动,引入动网格文件控制物体周围网格的运动,动网格文件采用六个自由度刚体运动求解器,给楔形体一定初速度自由下落。计算控制文件中计算时间从0到设定时间,每隔一定时间步长输出一次结果,并调用函数,输出每个时间步长时候楔形体表面测点的动压力值和楔形体整体的受力结果。数值模拟时利用mpirun将多块计算域同时进行计算以实现并行计算,提高计算效率。 该程序包主要包括以时间命名的数据文件夹,其中初始状态就是名为0 的文件夹,里面有alpha.water.txt、p_rgh.txt 和U.txt 等求解器对应所需的参数文件;其次是constant 文件夹,包括网格信息文件夹、polyMesh 和众多性能文件;最后是系统控制文件夹system,包括计算控制文件controlDict.txt、离散格式文件fvSchemes.txt和离散方程文件fvSolution.txt等。 网格划分采用OpenFOAM 自带的SnappyHexMesh 网格划分工具,它比Gambit 等网格划分工具功能更加强大。SnappyHexMesh 可以自动从STL、OBJ 文件生成六面体网格,通过迭代将一个初始网格细化。 本文采用的楔形体舱段模型基于骆寒冰等[8]的入水砰击试验,模型的主尺寸长×宽×高为1.440 m×1.354 m×0.746 m,模型底部斜升角为20°,模型总重180 kg,模型横剖面结构示意图如图1。模型底部为加筋板结构,左右舷各有三根纵骨,两根肋骨。在加筋板板格中心位置布置了8 个压力测试点(P1-P8),位置左右对称;在纵骨和肋骨上布置了26 个应变测试点(S1-S26),在模型的前后对称位置分别布置了两个加速度传感器(A1、A2)。测点布置如图2。实验水池的主尺寸长×宽×高为5.00 m×4.40 m×1.30 m,实验时候水深为1.20 m。模型试验现场见图3。采用日本共和KYOWA 公司的压力传感器,数据采集系统为DH-5922 动态信号测试分析系统,采样频率为10 kHz。 图1 模型横剖面结构示意图 Fig.1 Mid-section structure of the model 图2 模型测点布置示意图Fig.2 Distribution of measuring points on the model 图3 入水砰击模型现场 Fig.3 The model for water entry test without roll angle 图4 无转角楔形体数值模拟模型示意图Fig.4 The model in OpenFOAM without roll angle 实验模型的转角可以变化,无转角对称入水时,楔形体左右两侧斜升角都为20°,如果转动5°,那么楔形体左右两侧非对称,斜升角分别为15°和25°。根据该模型的无转角和有转角试验工况,本文将开展数值模拟,对比研究入水过程的加速度和砰击压力结果。 表1 不同网格数量的模型参数Tab.1 Models with different mesh sizes 图5 无转角楔形体模型内部3D网格 Fig.5 3D fluid meshes of the model 图6 楔形体局部网格Fig.6 Local fluid meshes around the wedge model 图7 无转角楔形体网格横剖面图 Fig.7 Model meshes in transverse direction 图8 无转角楔形体网格纵剖面图Fig.8 Model meshes in longitudinal direction 考虑到入水砰击试验采用的压力传感器直径为0.006 m,分别建立了三个计算模型,最小网格尺寸为0.01 m、0.006 m、0.005 m,对应的网格总数分别为157万、642万、989万。针对989万网格模型,图5显示了用中横剖面、中纵剖面剖出的水、空气和楔形体模型内部三维网格,气液相交处的网格进行了加密,楔形体周围区域的网格尺寸最小,图6 为楔形体周围局部网格。图7-8 显示了模型网格横剖面和纵剖面图。为保证每个网格的库朗数小于1,根据最大速度与最小网格尺寸计算时间步长取0.000 1 s。采用了k - ω SST湍流模型,根据经验公式,计算参数k和ω的值,分别取0.02和2。数值模拟工作站的处理器为Intel Core i7-6700CPU@3.40 GHz,四核八线程,8 MB 三级缓存,内存为24 G,操作系统为Ubuntu16.04LTS 64位。表1显示了三个模型的网格划分情况,以及整个数值模拟过程所用时间。 对表1中的三个不同网格密度模型数值模拟结果与试验结果进行了对比(见图9),考虑到无转角入水实验左右压力实验结果的对称性,选取右侧压力测点结果进行分析。图9 中列出了P5、P6、P7 测点位置砰击压力峰值对比示意,其中横坐标“Model 1”、“Model 2”、“Model 3”、“Test”分别表示三个不同网格模型和入水实验模型。可以看出,随着网格尺寸逐渐减小,测点压力峰值呈现增大趋势,Model 2 比Model 1 的结果明显大,不过,Model 2和Model 3 的模拟结果差异不大,Model 3 的结果与实验值吻合最好。认为Model 3的网格模型可以合理模拟砰击压力,接下来,将从时域角度对比分析Model 3模型的模拟结果。 图9 不同网格尺寸模型与模型实验的测点砰击压力峰值对比Fig.9 Comparison of slamming pressures peaks between numerical models and tests 图10 无转角入水加速度时域结果对比 Fig.10 Comparison of acceleration results 图11 无转角测点P5点压力时域结果对比Fig.11 Comparison of pressure results on P5 图12 无转角测点P6点压力时域结果对比 Fig.12 Comparison of pressure results on P6 图13 无转角测点P7点压力时域结果对比Fig.13 Comparison of pressure results on P7 (2)液面升高没有到达测点前,砰击压力为0,到达测点后,脉冲增大达到峰值,然后再缓慢减少。随着入水深度增加,测点砰击压力峰值呈现减少趋势。P5 测点数值模拟、模型实验压力峰值分别为101.2 kPa、115.7 kPa,数值模拟峰值偏小12.5%,不过,峰值出现的时刻都是0.018 3 s;P6 测点数值模拟、模型实验压力峰值分别为72.6 kPa、75.5 kPa,出现时刻分别为0.029 0 s、0.030 6 s,数值模拟峰值偏小3.8%,出现的时刻略早于实验结果;P7测点数值模拟、模型实验压力峰值分别为33.3 kPa、30.9 kPa,出现时刻分别为0.045 7 s、0.049 2 s,数值模拟峰值偏大7.7%,出现的时刻略早于实验结果。 由上述分析可见,入水加速度、各个测点砰击压力时域结果数值模拟和模型实验吻合较好。采用本文提出的OpenFOAM 数值模拟算法,包括参数选择、模型网格划分等,可以合理地模拟无转角楔形体入水砰击过程。 对于Model 3数值模拟的结果,选取0.02 s、0.04 s、0.06 s三个时刻,给出了压力云图(如图14)。考虑对称性,选取楔形体长度方向中间位置所在的中横剖面右半部分,图(a-1)、(b-1)、(c-1)分别显示了三个时刻的二维剖面流体压力云图及流体射流情况。图(a-2)、(b-2)、(c-2)分别显示了三个时刻的楔形体模型下表面的三维压力云图。可以看出: (1)随着入水深度增加,各个二维压力云图清楚地显示了压力峰值从楔形体下部往上方移动的过程,液面升高处压力最大,越向上部移动,压力峰值越小。也可以观察到局部射流发展过程,随着入水深度增加,射流向楔形体上方移动,0.06 s时射流已经超过楔形体折角位置。 (2)数值模拟楔形体表面的砰击压力,沿楔形体长度方向具有一定的三维效应,也就是说,楔形体中部位置压力较大,两端位置的压力略小。不过,从三维压力云图中可以看出,压力小的两端长度占整体长度比例不大。考虑到楔形体长度L = 1.44 m,半宽B = 0.677 m,L/B>2.0,流体流动的三维效应所造成砰击压力的三维效应不明显。实际模型实验时候,楔形体两端有首尾封板,有利于减少流体流动三维效应。 图14 不同时刻砰击压力云图及射流Fig.14 Pressure contours and water jets at different times 为了更清楚地说明三维效应,沿楔形体长度方向取三个横剖面,位置分别在1/2 L、1/4 L、1/8 L处,对比不同横剖面的相同高度测点在入水过程中砰击压力。入水模型实验以及第3.2节数值模拟的压力测点位置位于1/2 L 横剖面处,同样在1/4 L、1/8 L 横剖面的相同高度位置取相应测点,各个测点分别标记为P5-1、P5-2、P5-3、P6-1、P6-2、P6-3,测点P5-1、P6-1 对应第3.2 节中的P5、P6。图15-16显示了各个剖面测点的动压力时域结果。P5-1、P5-2、P5-3测点数值模拟峰值分别为101.2 kPa、99.6 kPa、93.7 kPa,P6-1、P6-2、P6-3 测点数值模拟峰值为72.6 kPa、67.5 kPa、60.5 kPa。可见,在长度方向(1/8 L,7/8 L)区间范围,楔形体表面砰击压力的三维效应不明显。 图15 无转角测点P5点不同剖面时域结果对比Fig.15 Comparison of pressure results on P5 图16 无转角测点P6点不同剖面时域结果对比Fig.16 Comparison of pressure results on P6 模型实验时候,利用一套机构可以控制楔形体的转角。围绕楔形体模型中上部的转动轴,角度最大可以转动到10°,这样,不仅可以做无转角对称入水砰击模型实验,也可以做有转角时候的非对称入水实验。本部分选取了转动角度5°、下落高度为0.3 m的实验工况进行数值模拟研究。 图17 有转角楔形体数值模拟示意图Fig.17 The model in OpenFOAM with roll angle of 5 degrees 图18 有转角楔形体网格横剖面图Fig.18 Model meshes in transverse direction with roll angle 图19 有转角楔形体网格纵剖面图Fig.19 Model meshes in longitudinal direction with roll angle (2)随着入水深度增加,两侧测点的砰击压力峰值各自呈现减少趋势,即P4>P3>P2,并且P5>P6>p7。由于楔形体左侧斜升角15°,右侧25°,左侧测点压力峰值大于右侧测点的,P4>P5,P3>P6,P2>P7,并且左侧对应位置测点出现峰值的时间比右侧的早; 图20 有转角入水加速度时域结果对比Fig.20 Comparison of acceleration results (3)左侧压力测点,P4数值模拟、模型实验压力峰值分别为50.9 kPa、66.8 kPa,数值模拟峰值偏小23.5%,出现的时刻分别是0.031 7 s、0.031 8 s;P3 测点数值模拟、模型实验压力峰值分别为42.5 kPa、51.2 kPa,出现时刻分别为0.046 2 s、0.048 1 s,数值模拟峰值偏小16.8%,出现的时刻略早于实验结果;P2测点数值模拟、模型实验压力峰值分别为22.8 kPa、25.1 kPa,出现时刻分别为0.065 8 s、0.049 4 s,数值模拟峰值偏大8.8%,出现的时刻略早于实验结果; 图21 有转角测点P4点压力结果对比 Fig.21 Comparison of pressure results on P4 图22 有转角测点P3点压力结果对比Fig.22 Comparison of pressure results on P3 图23 有转角测点P2点压力结果对比 Fig.23 Comparison of pressure results on P2 图24 有转角测点P5点压力结果对比Fig.24 Comparison of pressure results on P5 图25 有转角测点P6点压力结果对比 Fig.25 Comparison of pressure results on P6 图26 有转角测点P7点压力结果对比Fig.26 Comparison of pressure results on P7 (4)右侧压力测点,P5数值模拟、模型实验压力峰值分别为25.6 kPa、24.9 kPa,数值模拟峰值偏小2.5%,出现的时刻分别是0.035 1 s、0.035 4 s;P6 测点数值模拟、模型实验压力峰值分别为12.7 kPa、13.2 kPa,出现时刻分别为0.060 6 s、0.063 6 s,数值模拟峰值偏小4.7%,出现的时刻略早于实验结果;P7测点数值模拟、模型实验压力峰值分别为5.4 kPa、6.5 kPa,出现时刻分别为0.102 3 s、0.102 8 s,数值模拟峰值偏大15.8%,出现的时刻略早于实验结果。 由上述分析可见,入水加速度、各个测点砰击压力时域结果数值模拟和模型实验吻合较好。采用本文提出的OpenFOAM数值模拟算法,可以合理地模拟有转角楔形体非对称入水砰击过程。 图27 有转角不同时刻砰击压力云图及射流Fig.27 Pressure contours and water jets at different times with roll angle 对于有转角数值模拟的结果,选取0.04 s、0.06 s、0.08 s 三个时刻,图27 列出压力云图以及砰击射流情况,各个图例的含义同3.3节。可以看出: (1)随着入水深度增加,二维压力云图清楚地显示了压力峰值从楔形体下部往上方移动的过程,越向上部,压力峰值越小;由于左侧斜升角15°小于右侧25°,各个时刻左侧液面升高处砰击压力峰值明显大于右侧的,左侧的射流比右侧的更加明显,砰击更加剧烈; (2)数值模拟楔形体表面的砰击压力,沿楔形体长度方向具有一定的三维效应,不过,流体流动的三维效应所造成砰击压力的三维效应不明显。有转角非对称入水情况下,砰击压力的数值模拟和模型实验的结果具有可比较性。左侧液面升高处的压力峰值明显大于右侧的。 针对无转角和有转角楔形体舱段入水砰击问题,本文采用OpenFOAM 开源软件,开发了入水砰击的程序包,开展了数值预报研究工作,并与入水砰击模型实验进行了对比分析。得到了以下结论: (1)本文提出了有效预报三维舱段模型入水砰击问题的数值模拟方法。开发了基于两相流求解器InterDyMFOAM 数值模拟结构入水砰击的程序,包括初始状态、constant以及系统控制文件夹。采用有限体积法求解粘性不可压N-S方程系统,使用VOF方法对自由液面进行捕捉,并且引入了动网格技术,使用并行计算方法。采用RAS雷诺时均模型中的k-ω SST湍流模型。 (2)应用该算法数值模拟了某三维楔形体舱段的入水砰击过程。分别选择有转角与无转角的一个典型工况,模型最小网格尺寸选取为0.005 m,时间步长取0.000 1 s。预报了测点压力以及加速度时域结果,包括其峰值大小及其出现时刻,与模型实验结果吻合较好。讨论了入水砰击的三维效应。数值预报的砰击压力云图以及射流情况,合理描述了有转角和无转角的入水砰击过程。反映该算法能够合理有效地预报三维舱段模型入水砰击问题,并且该算法具有推广应用于更加复杂的三维船首砰击问题的潜力。2 楔形体舱段计算模型



3 无转角入水砰击载荷研究
3.1 数值模拟网格模型及算法参数选择
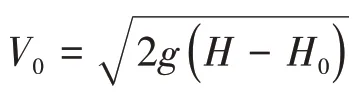



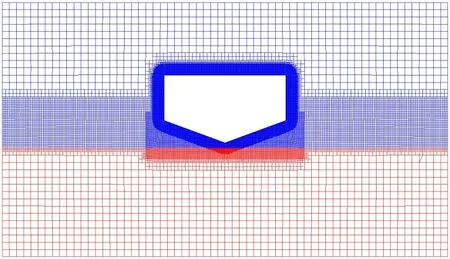

3.2 入水加速度及测点砰击压力时域结果对比分析
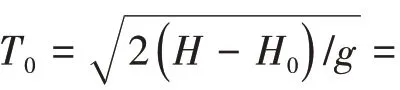

3.3 入水过程压力云图及三维效应分析
4 有转角入水砰击载荷研究
4.1 有转角入水砰击数值模拟网格模型




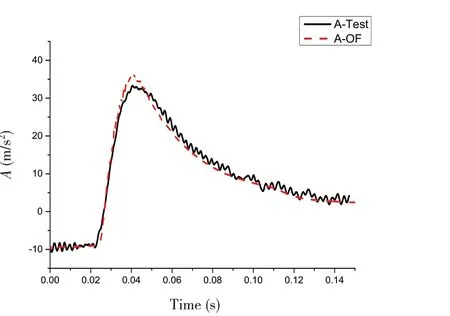
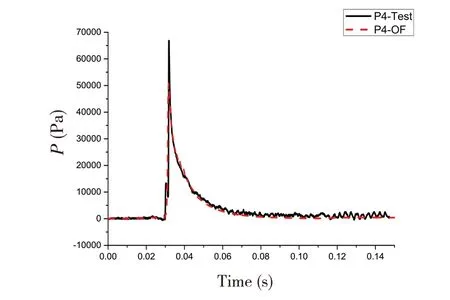
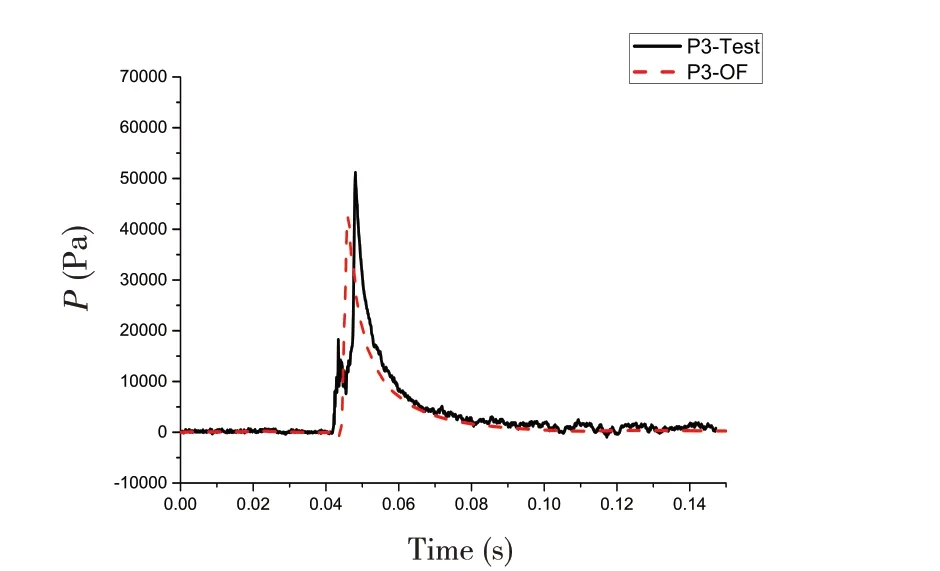
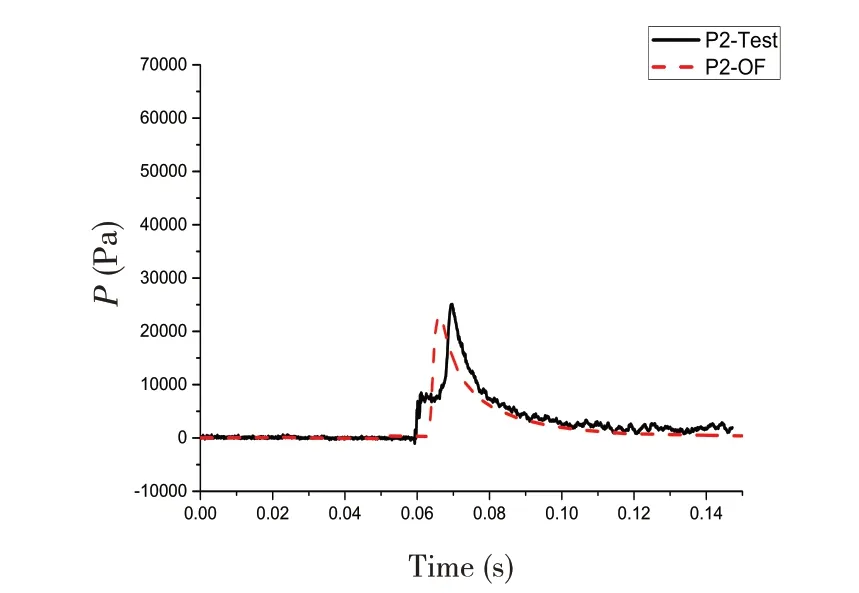
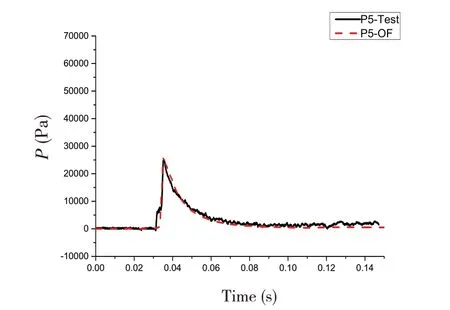
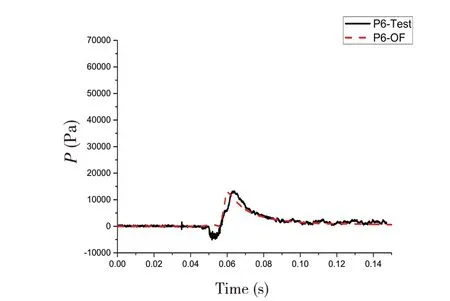
4.2 有转角入水加速度及测点砰击压力时域结果对比分析

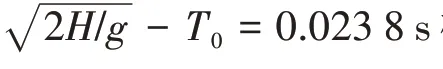
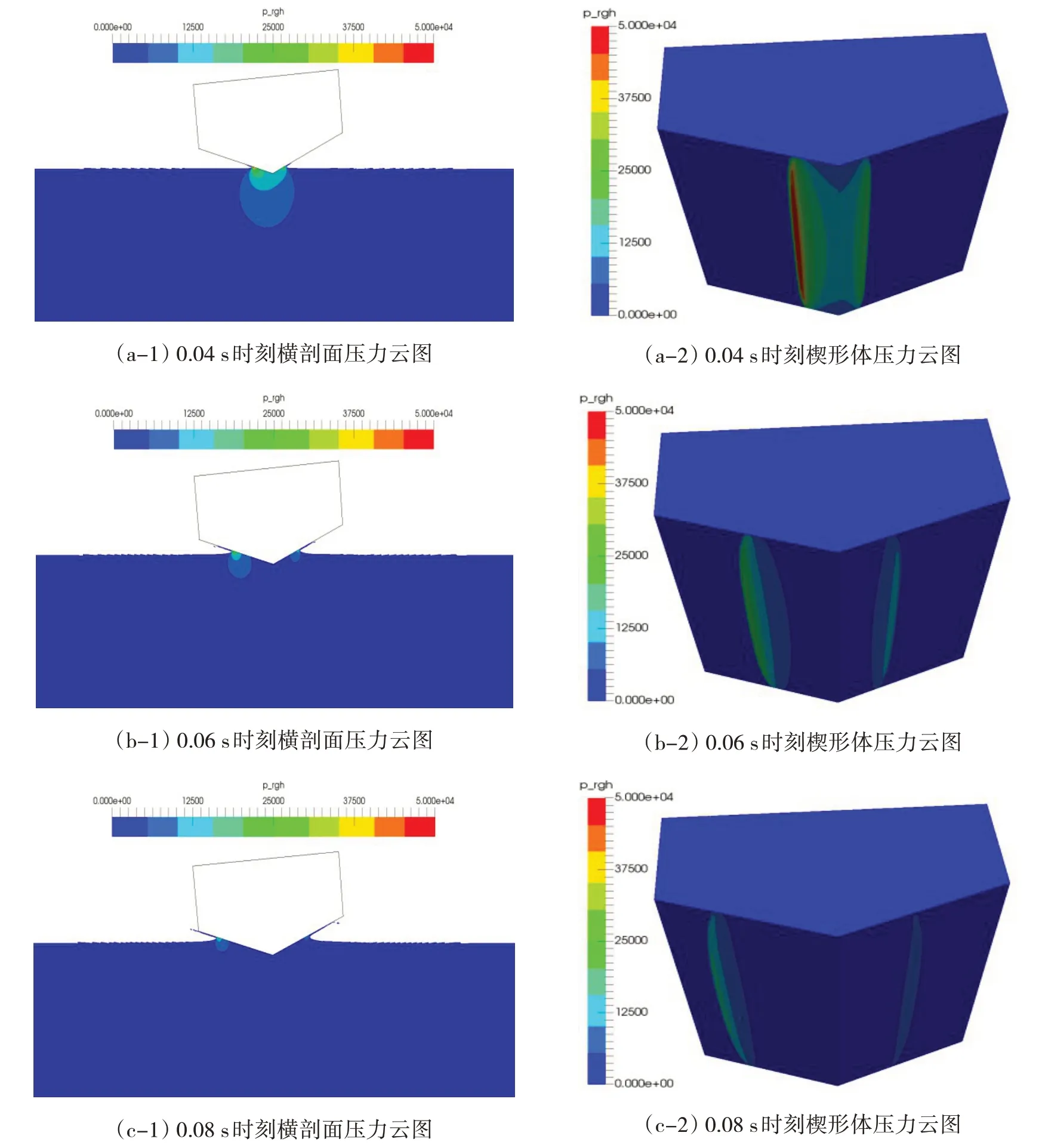
4.3有转角入水过程压力云图分析
5 结 论

