基于动刚度功率流法的组合板结构振动特性分析

钟奎奎，李江涛，吴文伟，李 慧

（1.中国船舶科学研究中心，江苏无锡214082；2.中国船舶及海洋工程设计研究院，上海200011）

0 引 言

船舶双层底是以板架组成的典型船舶结构，包含有外底板、桁材、内底板等。双层底的振动特性一直以来都是非常重要的研究课题，本文将双层底视为板架的组合结构来研究。板壳结构的振动在低频段以弯曲波为主，而目前对板壳振动的研究也主要集中于弯曲波，在高频段，纵波的影响不可忽略，此时，在组合板结构间，弯曲波和纵波会发生波型转换，从而使组合板结构的振动特性变得更为复杂。因此，以复杂板壳结构为特征的船体结构振动研究有很高的学术价值，受到国内外同行的持续关注。

长期以来，功率流方法（PFA）一直都是描述结构振动响应特性非常有效的方法[1-3]。振动的传递，本质上就是一种能量的传递。功率流能够简单有效地评估从能量源到接受者的能量传输。功率流包含力和速度幅值的大小，同时也考虑了它们之间相位的关系，直接给出振动传递的绝对度量值，是研究复杂板结构振动的有效方法。目前，对于功率流方法的研究，更多地集中于导纳法上[1-2]，但是，这种方法在解决多个子结构的复杂组合结构的动力学问题时会很困难，随着子结构数量的增加，整体结构的导纳矩阵的组装程序会变得非常复杂，有时甚至是无法组装[3-4]。

动刚度法借用有限元法的刚度阵组装策略来获得组合结构的总体动刚度矩阵，避免了导纳法中导纳矩阵难以组装的问题。而且，和导纳法一样，动刚度法只需要将整体结构离散成很少的子单元。因此，基于动刚度法研究组合板结构的功率流是很有前景的研究方向。

动刚度法已成功地应用于研究平板结构的面内振动和弯曲振动[5-6]，李慧[7]采用动刚度法时考虑了对边简支平板的面内振动和弯曲振动。Nefovska-Danilovic和Petronijevc[6]推导了任意边界条件的矩形薄板的面内振动的动刚度法公式。

本文采用动刚度法，研究复杂组合板结构的功率流特性，同时计入了纵波、剪切波与弯曲波，提出基于动刚度法的功率流分析技术。首先分析了L 型板在均匀激励下的位移空间分布及频率响应，之后，分析了双层底的振动响应及功率流，为工程中板结构的减振降噪提供了一定的指导依据。

1 动刚度法建模

1.1 平板模型描述

如图1（a）所示为典型的组合板结构及全局坐标系OXYZ，各板之间刚性连接，相互之间的夹角分别为β1和β2，局部坐标系oxyz附于其上。为建立平板动刚度单元，从图1（a）任取一个平板作为动刚度单元，如图1（b）所示，该平板两对边简支，由符号“S”表示，另外两边自由。为不失一般性，假定图1（b）中平板尺寸为Lx×Ly，板厚为h。

图1 典型组合板和对边简支矩形板Fig.1 Typical combination plate and rectangular plate with two opposite sides simply supported

1.2 局部坐标系下平板动刚度阵推导

根据薄板理论，图1（b）中平板振动控制方程为

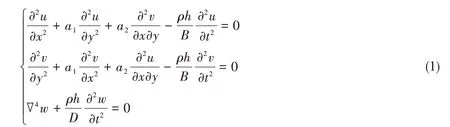
式中：u，v，w分别表示x，y，z方向的位移。

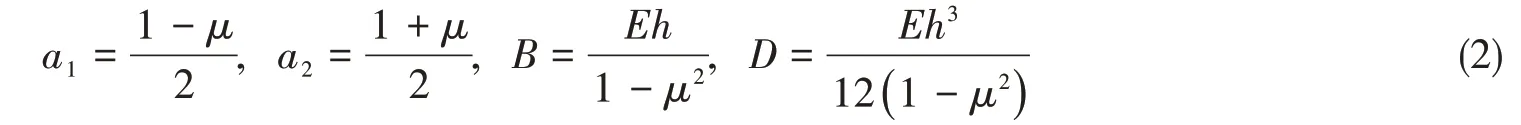
其中B为拉伸刚度，D为抗弯刚度，E为弹性模量，ρ为密度，μ为泊松比。考虑到能量损耗，用复弹性模量EC= E( 1 + i ⋅δ )代替弹性模量，其中δ = 2η，η为阻尼比。

对边简支矩形板的面内位移和弯曲位移可以写成

相应地，平板边界上的力和力矩可以表示成

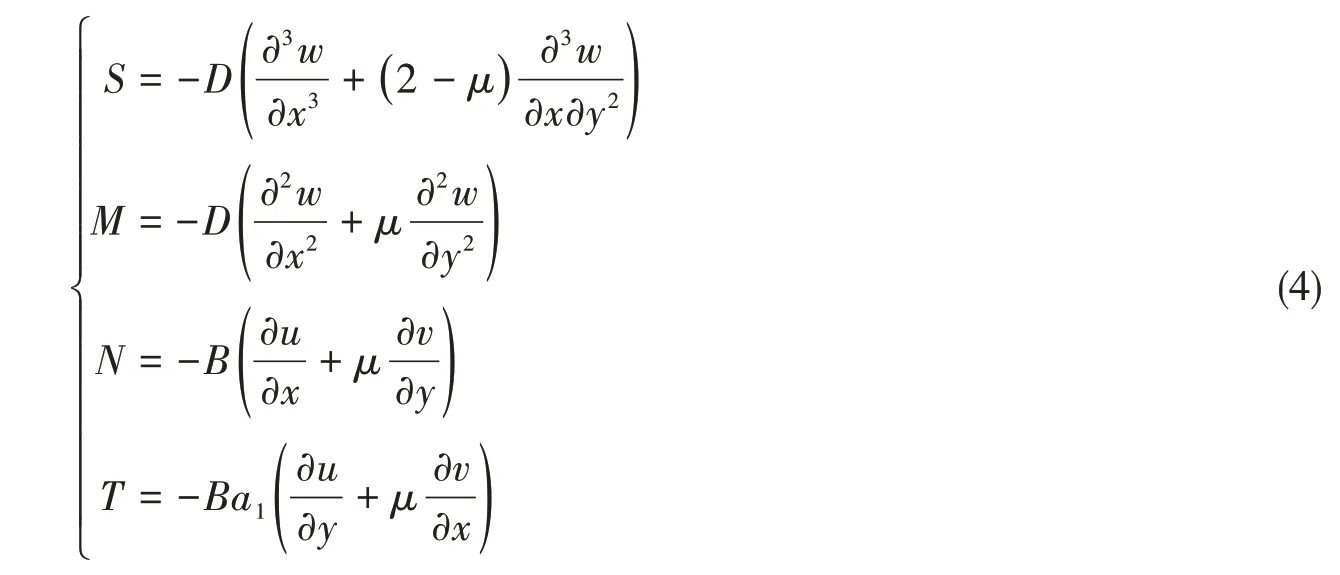
为导出动刚度矩阵，需建立平板边界上的位移和力向量之间的关系。位移和载荷暂写成如下形式：

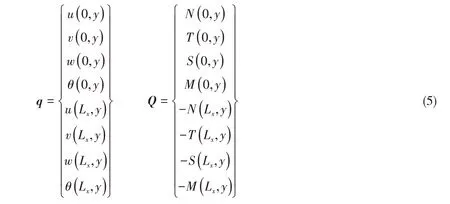
采用投影法，将（5）式在任意模态空间内投影，经过推导，可以得到局部坐标系下平板单元的刚度阵；之后采用有限元法单元组装的方法，得到整体坐标系下的系统动刚度矩阵[7]。

2 功率流计算公式

假设分布力F ={ }

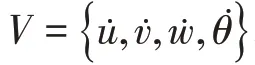
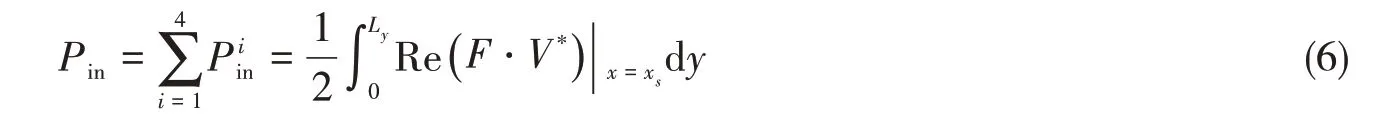
式中，V*是V的共轭复数。输入功率可以被分为面内纵波、面内剪切波和弯曲波的共同作用。面内纵波引起的输入功率可以表示成如下形式

面内剪切波功率流可以表示成

弯曲波相关的输入功率为

如果将组合板结构沿着它们各自的连接边界离散成一个个板单元，那么沿着连接边界的内力可以被看成是板单元受到的外激励力。当板与板的边界振动响应求出来之后，内力F′可以根据（7）-（10）式推导得到。因此，从一块板到另一块板的传输能量可以表示成

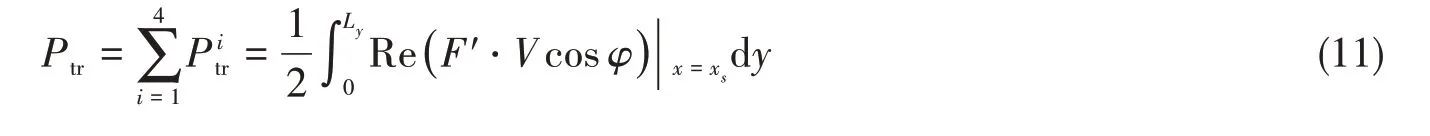
3 数值结果及讨论

3.1 数值验证

如图2所示，两个相同的平板以120°角刚性连接在一起，其材料参数和几何尺寸如表1所示。本次计算两个工况，即在平板1的CD边上分别受到垂向分布力和y向分布弯矩的简谐激励（单位幅值）。计算频段为10-2 010 Hz，计算截断项取N=10即可得到良好的结果[7]。

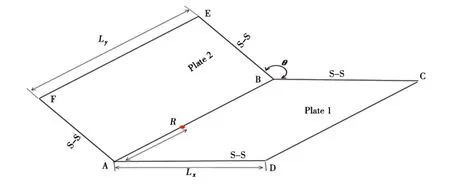
图2 L型板计算模型Fig.2 Calculation model of L-shaped plate

表1 矩形板具体参数Tab.1 Geometry and material parameters of plate

如图3所示，在均布激励下，AR= Ly/3平板上R点的垂向位移DSM 计算值同有限元计算结果吻合良好。其中，在400 Hz 以内弯曲振动的峰值出现的频率均高度一致，而随着频率的提高，峰值出现的频率相差较大，主要原因在于随着频率的增高，有限元方法的计算不确定性逐渐增大，同时，DSM的截断项取10 对高频振动的模拟不够充分。因此，忽略共振处出现的微小偏差，有限元计算结果和动刚度法计算位移曲线趋势是一致的，且处在同一量级，计算结果吻合良好。

图3 垂向分布力作用下点R的垂向振动位移曲线Fig.3 Vertical vibration at point R for the plates excited by uniformly distributed perpendicular forces

类似地，图4 给出均布弯矩作用下，平板点R 的面内位移曲线，在400 Hz 以内面内振动幅值和有限元结果吻合良好，随着频率的提高两者差异较大，但是趋势一致。但是，需要说明的是，文中的双板结构在受到激励时，其内部同时存在面内振动和弯曲振动，而且两者耦合。因此，图3 和图4 表明，动刚度法可以比较精确地模拟结构面内振动、面外振动及其耦合问题。

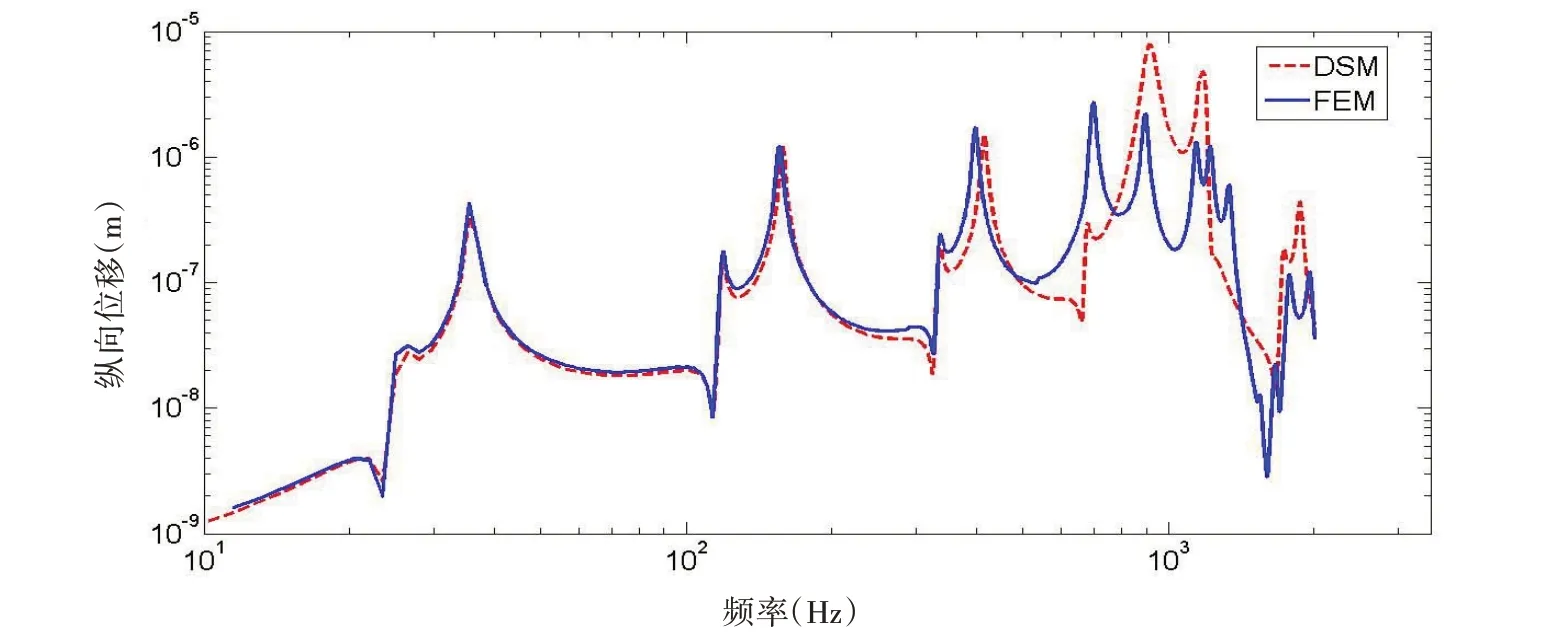
图4 均布弯矩作用下R点的纵向振动位移曲线Fig.4 Longitudinal displacements at point R for the plates excited by uniformly distributed bending moments

同时，本文给出了在200 Hz时两种不同激励作用下的平板位移云图。可以发现，通过动刚度法得到的振动位移云图和有限元法吻合良好，有着相同的幅值峰值和谷值。这为后续深入研究复杂板结构的振动传递、波形转换和波传播规律提供了算法基础。

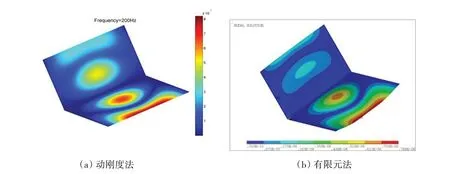
图5 垂向分布力作用下200 Hz时的振动位移云图Fig.5 Displacement nephogram at 200 Hz for the plates excited by uniformly distributed transverse forces

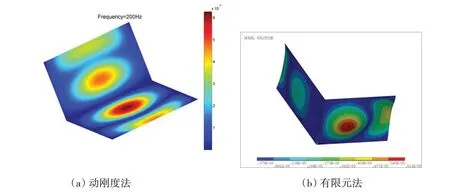
图6 均布弯矩作用下200 Hz时的振动位移云图Fig.6 Displacement distributions at 200 Hz for the plates excited by uniformly distributed bending moments

3.2 功率流计算分析

首先计算图2 所示L 型矩形板输入功率流及输出功率流，计算结果如图7 和图8 所示。图7 给出了板1的输入功率流曲线和板2的传输功率流曲线。可见，输入功率流和传输功率流在共振频率处同时到达了峰值；同样地，在反共振频率处，输入功率流和传输功率流都同时达到了低谷。也就是说，当平板在共振频率处被完全激励时，结构中可以得到更多的振动传输能量，而且从图7中我们还可以看到，在共振频率处，几乎所有的振动能量都被传输到板2，而在反共振频率处，则是很少的一部分能量被传输到板2中。

图7 垂直分布力作用下板的功率流Fig.7 Power flow results for plates driven by uniformly distributed perpendicular forces

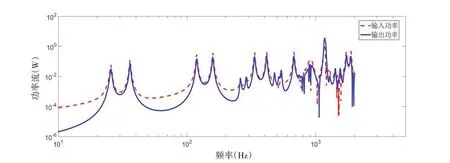
图8 均布弯矩作用下板的功率流Fig.8 Power flow results for plates driven by uniformly distributed bending moments

同样地，图8给出了外载荷为弯矩时的功率流曲线。同样可以发现，输入功率流和传输功率流在共振频率处同时到达峰值。

除了研究板结构内的功率流之外，振动传输路径在研究组合板结构的动力学特性中也有很重要的作用[8-9]。Feng等人[9]对一个梁-圆柱壳体结构中的功率流进行了研究分析，并且还对比了三种不同的能量传输路径，并最终确定了最主要的传输路径。基于动刚度法也可以对结构的能量传输路径进行一个直观的描述。

图9 双层底舱段模型Fig.9 Model of double-bottom tank

图9 所示为一典型船舶双层底结构的简化模型，由19 块板组合而成。计算其在上甲板，即板5中心受单位简谐垂向点激励作用下的结构功率流密度向量的幅值云图。

图10 为双层底舱段模型的正视图。双层底长10 m，材料参数和表1所列出的一致。

图11 为在频率为200 Hz 时双层底整体结构的功率流云图。可见，除了板5 之外，很少有能量传递到其它板，因此板5 也是在此点激励下振动控制的主要目标。为了更进一步研究功率流的传播路径，我们也可以作功率流的矢量分布图。

图10 双层底舱段正视图Fig.10 Front view of double-bottom tank model

图12-13 分别为板5 及板4 的功率流矢量分布图，由图可知由于点激励施加于板5的中心及结构的对称性，各板的功率流分布也有着不同的对称性。由图12 可知，受力点处的功率流幅值在板5 中并不是最大的，而且在其周围（图12 中矩形框范围内），功率流的传输方向都指向受力点。由图13 可知，在板4 中，功率流的传输并不仅仅是由与受激板相连的边向板其余各处传播，在图13 中矩形框范围内的功率流也有着明显的向外传播的特性。这是因为功率流取决于内力和其速度响应幅值及其之间的相位角，当相位角小于90°时，功率流的符号为负，吸收能量；而当相位角位于90°和180°之间时，功率流的符号为正，输出能量。

由以上分析可知，动刚度功率流法能够研究整个模型中功率流的传播路径，可为结构的减振降噪提供直观的理论依据。

图11 双层底功率流云图Fig.11 Power flow diagram of double bottom

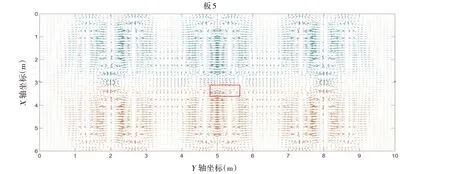
图12 板5功率流矢量图Fig.12 Power flow vector diagram of plate No.5

图13 板4功率流矢量图Fig.13 Power flow vector diagram of plate No.4

4 结 语

本文基于动刚度功率流法，并且将板的面内振动和面外振动同时考虑在内，分析了组合板结构的振动特性，为进一步深入研究板与板之间的波型转换打下了坚实的理论基础。本文通过对两个具体模型进行数值分析，充分研究了复杂组合板结构内的功率流特性以及能量传输路径等问题。与基于导纳法的功率流分析方法[1-3]相比，基于动刚度法的功率流分析方法更加适用于复杂组合结构的动力学特性研究，因为与传统的有限元方法一样，整体结构的总体动刚度矩阵可以通过简单直接的方法进行组装。