深松铲减阻性及耕作阻力影响因素研究—基于LS-DYNA

周 健，纪冬冬，李立君

(中南林业科技大学 机电工程学院，长沙 410004)

0 引言

目前，我国农业生产耕作中松土的方式主要有翻耕和深松两种。翻耕作业时会使土壤遭受耕作机具的挤压以及车轮的碾压，使其底部形成了坚硬的犁底层[1-2]。由于犁底层的存在，将土壤分割为两层，严重影响了农作物根须的生长与延伸，不利于营养物质的吸收与利用；同时，也影响了土壤中CO2、SO2、H2S、CH4等有害气体的交换与排放，使固氮及硝化减少，阻碍了微生物的活动，从而影响作物的生长，导致粮食产量下降[3]。由于翻耕作业对土壤的动土量比较大，使大量土壤颗粒裸露在地表从而造成风蚀现象，严重时形成沙尘暴。由于传统翻耕作业存在着诸多弊端，不利于农业的可持续发展，因此保护性耕作被提出，而深松技术是保护性耕作的重要支撑，可有效保证土壤表层不受破坏，遏制水土流失及荒漠化现象的发生[4]。深松铲作为深松机耕作的直接载体，其耕作阻力的大小直接决定了松土的效率及能耗，因此研究深松铲的减阻性具有重要意义。

近年来，国内外学者逐渐开始研究耕作部件的减阻性能：Gill等[5]对比了直线型和弯曲型耕作部件的工作阻力，结果表明直线型耕作时所受阻力要低7%～20%；陈坤[6]等设计了一种新型圆弧型深松铲，并进行了田间试验，结果表明该深松铲能有效改善松土效果、减少耕作阻力；王雪艳等[7]设计了一种自激振动的深松机，并与普通的深松机进行对比，结果表明自激振动的深松机可减少12.79%的阻力；郭志军等[8]通过研究分析家鼠前爪中指的挖掘特性，设计了弯曲型仿生深松铲，结果显示其具有较好的减阻效果；杨程光等[9]分析了深松耕作阻力的影响因素，结果表明选择合适的铲距可有效减小深松作用阻力。查阅文献发现，很少有研究者对不同触土曲面深松铲的减阻性能及土壤切削应力的分布进行研究，也很少涉及分析仿生变曲率的入土角对耕作阻力的影响。因此，本文通过对5种典型触土曲面方程进行研究，设计了5种不同结构的深松铲。同时，利用ANSYS/LS-DYNA软件对深松铲切削土壤过程进行模拟仿真，得出不同结构深松铲在切削土壤过程中的阻力变化以及土壤应力变化情况，对比分析得出减阻性能较好的深松铲结构；并对入土角、工作速度、工作深度等耕作阻力影响因素进行单因素试验，分析上述因素对深松铲松土阻力的影响，以期为降低作业功耗，减小深松耕作阻力提供一定的依据。

1 土壤模型

本文以农业耕作的土壤作为研究对象，由于土壤的成分和结构复杂，目前还没有一种理想的土壤模型来描述土壤遭受外力后的变化情况，根据土壤应力与应变的关系，土壤本构关系模型可大致分为4类:土壤线弹性模型、土壤弹塑性模型、土壤非线弹性模型和土壤流变模型。深松铲切削土壤属于侵彻问题，选择合适的土壤本构模型对仿真的可靠性至关重要。由于土壤不是理想的弹性或塑性材料，而是一种弹塑性材料，在受到外界载荷后，会使材料出现硬化和软化现象，应力与应变具有明显的非线性特征，因此本文将土壤视为弹塑性材料，该模型最能反映土壤遭受载荷后实际变形的情况[10-11]。

1999年，美国联邦公路局开始研究土壤材料在有限元分析中的模型，并在2000年完成了土壤本构模型的建立，2001年对土壤本构模型进行了初步的验证，2002年土壤本构模型正式成为LS-DYNA一种标准材料模型[12]。本文参考文献[13]，选用LS-DYNA材料库里面的MAT147 (MAT_FHWA_SOIL) 材料作为土壤仿真的本构模型，该模型采用修正的Drucker-Prager屈服准则，因为该屈服准则综合考虑了材料塑性硬化、塑性软化、应变速率效应和空隙水压力效应，使得仿真结果更接近实际情况。屈服准则的计算公式为[14]

其中，F为模型屈服表面力(N)；p为压力(Pa)；β为内摩擦角(°)；J2为应力偏张量的第二不变量；K(θ)为张量平面角函数；c为粘聚力(N)；α为修正后屈服面和标准 Mohr-Coulomb 曲面相似度。

结合本地土壤的实际情况，并参考Soil Material Model 147[15]，将仿真的土壤参数进行设置为(见表1)，采用kg-m-s-N-Pa单位制。

表1 土壤材料参数

2 深松铲结构设计

根据5种典型准线的方程，并结合深松铲和深松铲柄的行业标准(JB/9788-1999)，设计了5种不同结构的深松铲，利用SolidWorks三维软件完成对深松铲模型的绘制，如图1所示。上述5种模型具有相同的入土角、纵深比，整个深松铲高600mm、厚30mm。本深松铲材料选用20Cr，淬火后再低温回火，表面为高碳的回火马氏体耐磨，心部为低碳的回火马氏体耐冲击。

(a) 直线型 (b) 圆弧线型 (c) 摆线型

(d) 抛物线型 (e) 仿生变曲率线型

3 LS-DYNA仿真深松铲切削土壤

1) 网格划分：主要分析深松铲切削土壤阻力及土壤的应力分布情况，为了简化计算，将深松铲视为刚体，材料的本构模型采用MAT_RIGID，设置材料的弹性模量为2.07×105MPa，密度为7 830kg/m3，泊松比为0.254。为了缩短仿真计算时间，将土壤大小设置为700mm×400mm×400mm。由于模型具有对称性，因此选取模型的1/2作为分析研究对象，土壤材料模型选择MAT_FHWA_SOIL。由于该材料在Workbench材料库里面不能定义，需后续修改K文件来添加该材料模型[16]。因为深松铲和土壤模型结构较为简单，因此采用六面体网格进行划分，采用扫掠方法对深松铲进行网格划分，土壤采用映射方法进行网格划分，整个有限元模型划分的节点数共为299 145，单元数为281 288。图2为直线型深松铲切削土壤的有限元模型。

2) 定义接触：在深松铲切削土壤之前，其与土壤之间不能相互接触，同时两者之间的距离不易过大[17]，为了尽量节约计算空余时间，将深松铲与土壤的初始距离定义为10mm。由于在仿真过程中深松铲会穿透土壤，因此定义两者之间为面面接触，添加关键字*ERODING_SURFACE_TO_ SURFACE，将深松铲定义为接触部件，土壤定义为目标部件。

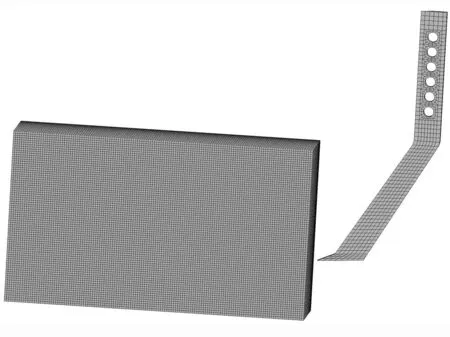
图2 直线型深松铲切削土壤的有限元模型

3) 初始条件：由于深松铲水平切削土壤，因此将其速度设定为1.666 7m/s (6km/h)进行仿真研究，土壤固定不动。

4) 边界条件：深松铲沿X水平方向切削土壤，故该自由度不约束，其余自由度均完全约束。由于在实际工作过程中，土壤是无边界的，为了防止深松铲与边界约束之间的土壤在切削过程中受到过分挤压而导致应力陡增，对土壤上顶面及周边施加无反射边界条件，同时对土壤底部施加全约束以固定，对称面在Z方向施加约束，深松铲与土壤接触的面不约束。

4 深松铲切削土壤仿真结果分析

4.1 切削阻力分析

图3为在切削速度为1.666 7m/s (6km/h)时直线型深松铲受到的阻力。由图3可知：深松铲在整个仿真切削过程中阻力波动较大，不利于结果分析，因此需对阻力图进行数字滤波，LS-DYNA的后处理软件中自带了4种滤波器，分别为SAE滤波、BW滤波、FIR100滤波和COS滤波[18]。本文选择常用的COS滤波，采用2点均值作为最终数据，截止频率设置为20Hz，得到滤波后的阻力如图4所示。将滤波后的信号与原始信号进行对比，发现信号经过COS滤波后能有效地消除信号中的噪声，且信号能较好地保持原始信号的基本特征。在0.006s内深松铲的阻力为0N，因为此过程深松铲逐渐靠近土壤模型，未产生切削作用；在0.006～0.125s内，深松铲的阻力逐渐增大，此过程为深松铲开始切削土壤到稳定切削；在0.125～0.30s内，深松铲的阻力基本不变，一直处于稳定切削过程，一半深松铲所受阻力为702N。

为了对比分析5种不同结构的深松铲在切削土壤过程中的阻力变化情况，对上述5种深松铲进行了LS-DYNA仿真，其稳定切削过程中的阻力对比如图5所示。由图5可知：圆弧型深松铲的阻力最大，为825N，而阻力最小的为仿生变曲率型深松铲，其阻力为601N，直线型、摆线型和抛物线型深松铲的阻力分别为702、712、692N。因此，仿生变曲率型深松铲在切削土壤过程中减阻性能最好。

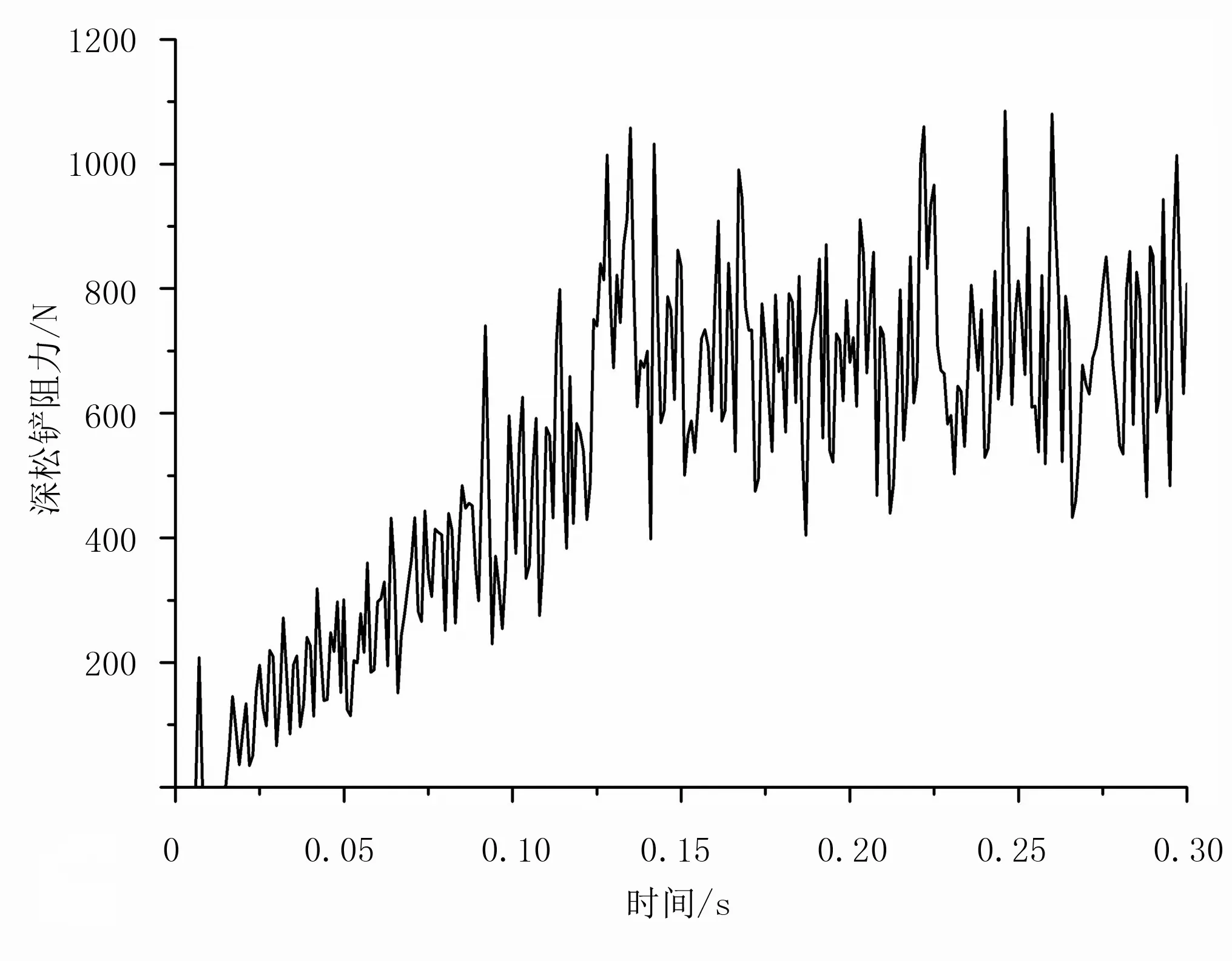
图3 直线深松铲切削土壤时所受阻力

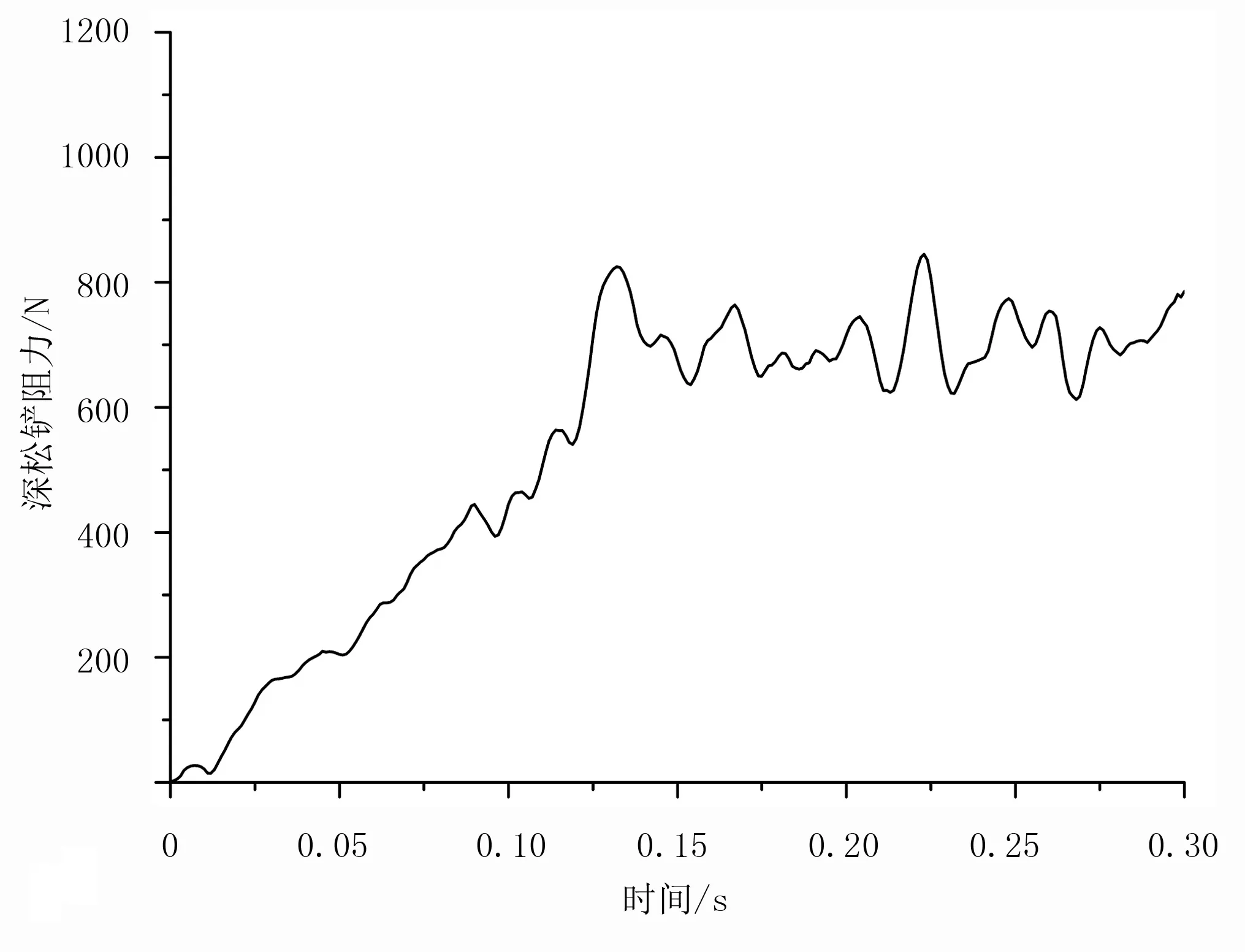
图4 数字滤波后直线深松铲切削土壤时所受阻

图5 5种深松铲受到的阻力

4.2 土壤等效应力分析

为了分析深松铲不同触土曲面对土壤扰动的影响，研究了在切削速度为 1.666 7m/s时，土壤在被稳定切削过程中(第2s)的应力分布情况。图6为5种不同类型深松铲切削土壤过程中的应力分布。由图6可知：深松铲在切削土壤过程中，应力分布主要出现在深松铲的触土曲面，直线型、圆弧型、摆线型、抛物线型和仿生变曲率型深松铲的最大应力分别为2.32、2.40、3.80、2.11、2.93MPa。直线型、圆弧型和抛物线型深松铲的铲尖均存在较大的应力分布，而铲尖相对而言较为脆弱，若长时间处于高应力下，容易导致其变形，从而使整个深松铲报废；摆线型深松铲虽然铲尖的应力较小，但深松铲的下端应力较大；仿生变曲率型深松铲的高应力区主要集中在上部，下端应力分布较小。

(a) 直线型 (b) 圆弧线型 (c) 摆线型

(d) 抛物线型 (e) 仿生变曲率型

5 不同工作参数对深松铲耕作阻力的影响

5.1 入土角对耕作阻力的影响

入土角的大小对深松铲阻力具有重要影响，选择合适的入土角可以明显改善深松铲的受力情况。从现有研究和实际情况来看，入土角一般选择20°～40°，入土角太大或太小不利于深松铲的使用[19]，因此本文选择20°、24°、28°、32°、36°作为入土角的5个试验水平。仿生变曲率深松铲在5种不同入土角下受到的阻力如图7所示，其工作深度为 280mm，速度为1.666 7m/s (6km/h)。由图7可知：入土角为24°时，深松铲切削土壤时所受阻力最小，为601N；入土角为20°时，深松铲阻力为 630N；当入土角大于24°时，深松铲的阻力随入土角的增大而增大。因此，当入土角为24°时，深松铲具有较好的减阻性能。

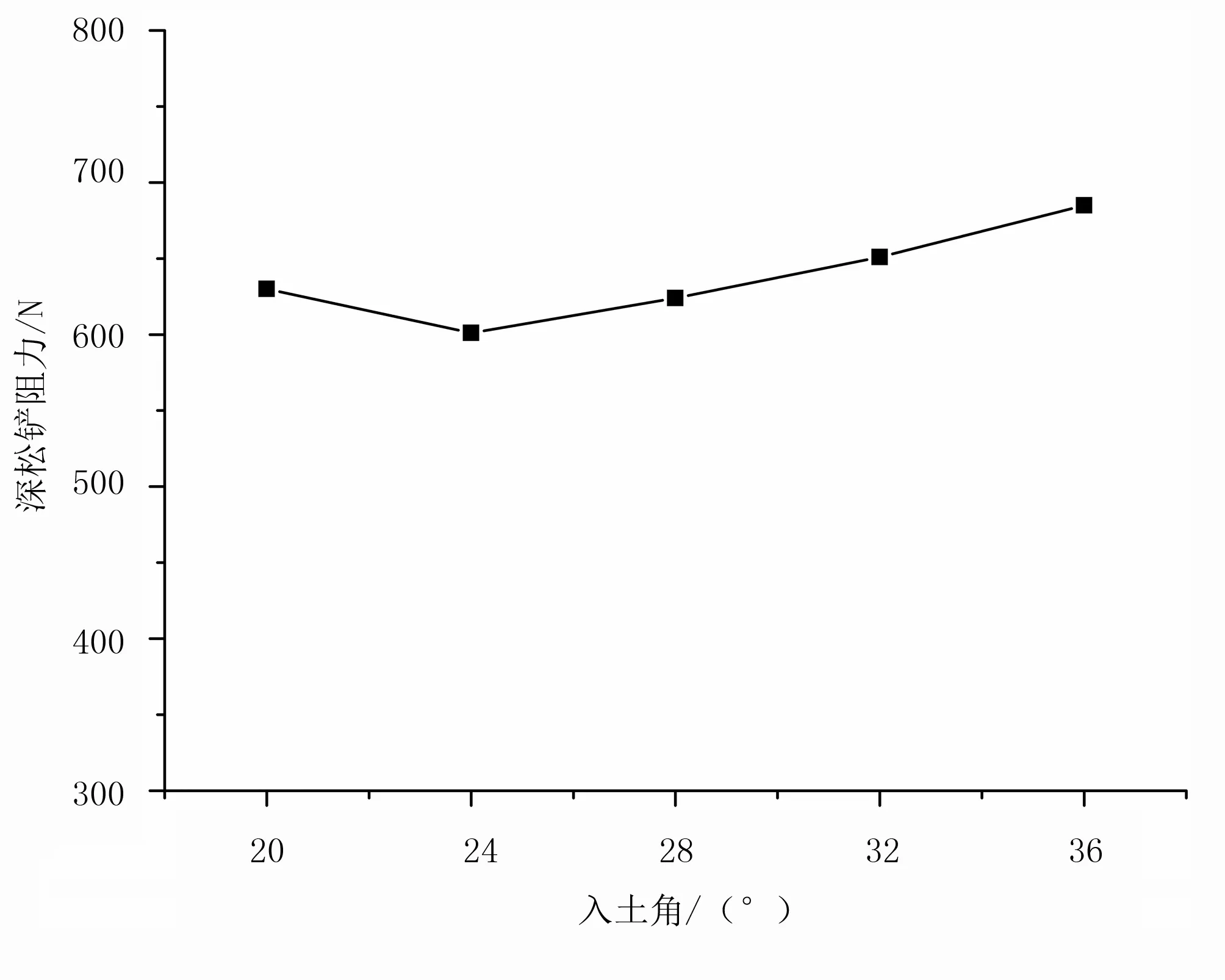
图7 不同入土角对深松铲阻力的影响

5.2 工作速度对耕作阻力的影响

为了研究在不同的工作速度下深松铲受到土壤阻力情况，对工作速度进行单因素试验仿真。根据深松铲实际工作的要求[20]，将工作速度设置为4、5、6、7、8km/h等5个试验水平，其工作深度为280mm，入土角为24°。图8为不同工作速度对深松铲耕作阻力的影响。由图8可知：深松铲切削土壤时，其阻力随工作速度的增加而增大，工作速度为4km/h时，其阻力最小，为530N；工作速度为8km/h时，其阻力最大，为689N。工作速度快，虽然能提高深松铲的工作效率但同时也会使工作阻力增大，增加能耗，因此在实际工作工程中，应根据具体的工作要求来选择合适的工作速度。

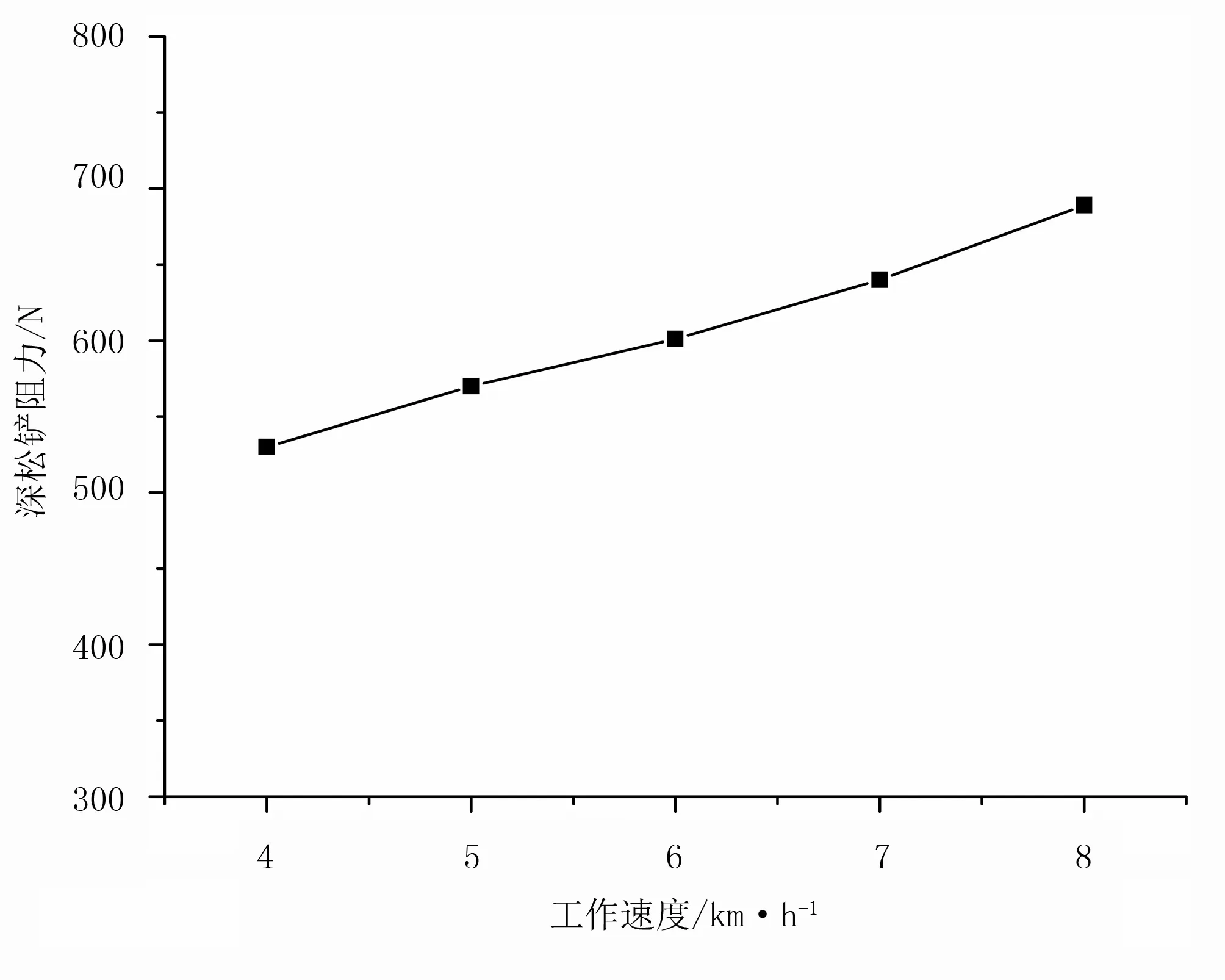
图8 不同工作速度对深松铲阻力的影响

5.3 工作深度对耕作阻力的影响

为了进一步研究不同工作深度对深松铲切削阻力的影响，对工作深度进行单因素仿真试验。根据深松铲实际工况的要求，将工作深度设置为160、190、220、250、280mm等5个试验水平，工作速度为6km/h，入土角为24°。图9为不同工作深度对深松铲耕作阻力的影响。

图9 不同工作深度对深松铲阻力的影响

由图9可知：深松铲在切削土壤过程中，其阻力随工作深度的增加而增大，在工作深度为160mm时，深松铲阻力最小为380N；在工作深度为280mm时，深松铲阻力最大，为601N。

6 结论

1)仿生变曲率深松铲的减阻性能最好，其阻力最小(601 N)，圆弧型深松铲的减阻性能最差，耕作阻力最大(825 N)。

2)深松铲入土角为24°时，其耕作阻力最小(601N)，入土角为20°时，深松铲阻力为 630N。当入土角大于24°时，深松铲的阻力随入土角的增大而增大，因此当入土角为24°时，深松铲具有较好的减阻性能。

3)深松铲的耕作阻力随工作速度和工作深度的增加而增大，在速度为8km/h，工作深度为280mm时，其耕作阻力均最大。