在计算机学习环境下问题表征转换对小学数学学习效果的影响

白现萍

(新疆师范大学预科教育学院，新疆乌鲁木齐830017)

0 引言

问题表征主要是指问题解决者依据自身的知识经验对觉察到的已知条件信息进行解释，把外部的刺激情境转化为内部心理符号，即构建问题的认知结构、形成问题图式的过程，问题表征对问题能否顺利解决起着至关重要的作用。根据已有研究，并梳理问题表征方式[1-4]，发现其中的图式表征与数学问题解决成正相关。从某种意义上说，图式表征是解决数学问题的一种比较有效的方式。数学学习的主要目的之一就是发展和组织认知表征从而理解数学概念[3]。本研究从图式表征入手，结合和倍问题的问题结构以及常用解题方法，将和倍问题的表征方式分为线段图表征方式和公式表征方式。

1 研究方法

1.1 被试

本实验的被试是江苏省南京市秦淮区四方小学五年级的176名学生。实验对象均已学过和倍问题的相关知识。根据回收的数据，将记忆测试、迁移测试、心理努力程度和次任务成绩中的无效数据剔除，剩余有效数据151份，其中男生80人，女生71人。

1.2 设计

本实验是对比实验，分为四个实验组：实验组1、实验组2、实验组3和实验组4。实验组1的自变量为问题表征单向转换为线段图；实验组2的自变量为问题表征单向转换为公式；实验组3的自变量为问题表征双向转换(将文字转换为线段图和公式)；实验组4的自变量为双向转换+逆转(将公式和线段图转换为文字题)。表征转换是被试间因素。两种表征方式的交互程度分别是：线段图(部分拖拽)和公式表征(部分填写)。因变量为记忆测试成绩和迁移测试成绩。

1.3 材料与工具

实验材料包括学习材料和测试材料。学习材料是由Flash制作的多媒体学习资源，如下图1、2、3、4、5、6所示，学习题目主要改编自苏教版小学数学课本的例题和练习题。学习材料的场景是通过完成闯关帮助小猴子回家。规定每个学生对学习材料只能进行一次且单向的学习。

首先进入学习材料的首页，要求学生输入自己的姓名，点击开始按钮，进行前测，接下来是游戏说明，点击Next按钮进入关卡选择，每个学习材料都是分三关进行。点击第一关后开始学习实验材料。学习之后，完成记忆测试、迁移测试、次任务测试和心理努力程度测量。最后完成所有实验项目，进入结束界面，点击保存按钮。

1.4 过程

实验在江苏省南京市四方小学五年级的四个不同班级进行的，人数分别为44、45、45、44人。整个实验过程在机房中进行，每个实验组的人数基本一致。

首先，实验者用一个简单的样本动画文件向被试演示如何操作实验材料。其次，实验者随机发放实验材料，每个班级随机分成三组，进行数字化学习资源的学习，实验过程中，实验者进行巡视，对不清楚操作的学生进行指导，学习时间为15分钟。最后，在规定的时间完成学习后，要求被试将保存的.txt文件上传至教师机。确保收到文件后，实验结束。

将收集到的数据，用SPSS软件进行分析和处理。

2 结果与分析

实验中，记忆测试和迁移测试均有3道题目，错误的题目记为0分，正确的记为1分，记忆测试和迁移测试的成绩都是3道题目分数的叠加。次任务有2道题目，错误的题目记为0分，正确的记为1分，总成绩是2道题目分数的叠加。心理努力程度的测试总共有9个选择项，选择1记为1分，选择2记为2分，选择3记为3分，选择4记为4分，选择5记为5分，选择6记为6分，选择7记为7分，选择8记为8分，选择9记为9分。

2.1 问题表征的不同转换方式对学习者学习效果的影响

将问题表征的四种转换方式的记忆测试和迁移测试成绩进行单因素方差分析，得到描述性统计分析表、方差齐性检验表和各组的多重比较表。

表1 问题表征的不同转换方式对学习者学习效果的描述性统计分析

表2 问题表征的不同转换方式对学习者学习效果的ANOVA分析

从表1可以看出，对于单项转换，单项转换为公式组的记忆测试成绩较高(M=1.52，SD=0.890)，迁移测试成绩较低(M=1.07，SD=0.867)，单项转换为线段图组的记忆测试成绩较低(M=1.08，SD=0.795)，迁移测试成绩较高(M=1.51，SD=0.768)；对于双向转换，其记忆测试成绩(M=1.46，SD=0.817)与单项转换为公式组相近(M=1.52，SD=0.795)，其迁移成绩(M=1.51，SD=0.818)与单项转换为线段图组相近(M=1.51，SD=0.768)；对于双向转换+逆转，其记忆测试成绩(M=1.84，SD=0.688)和迁移测试成绩(M=1.92，SD=0.759)均高于其他三组。从表2可以看出，记忆测试成绩F=5.534，p=0.001<0.05，迁移测试成绩F=7.287，p=0.000<0.05，说明各组之间的记忆测试和迁移测试成绩的均值存在显著性差异。

对于记忆测试成绩，单向转换为线段图组与单向转换为公式组之间存在显著性差异(p=0.016<0.05)，单向转换为线段图组与双向转换之间存在显著性差异(p=0.049<0.05)，单项转换为线段图组与双向转换+逆转之间存在显著性差异(p=0.000<0.05)，单向转换为公式组与双向转换之间不存在显著性差异(p=0.718>0.05)，单线转换为公式组与双向转换+逆转组之间存在显著性差异(p=0.045<0.05)，双向转换与双向转换+逆转组之间存在显著性差异(p=0.046<0.05)。

表3 问题表征的不同转换方式对学习者学习效果的多重比较

对于迁移测试成绩，单向转换为线段图组与单向转换为公式组之间存在显著性差异(p=0.016<0.05)，单向转换为线段图组与双向转换之间无显著性差异(p=0.997>0.05)，单项转换为线段图组与双向转换+逆转之间存在显著性差异(p=0.032<0.05)，单向转换为公式组与双向转换之间存在显著性差异(p=0.018<0.05)，单线转换为公式组与双向转换+逆转组之间存在显著性差异(p=0.000<0.05)，双向转换与双向转换+逆转组之间存在显著性差异(p=0.035<0.05)。

2.2 双向转换和双向转换+逆转对学习者学习效果的影响

将双向转换和双向转换+逆转的记忆测试成绩、迁移测试成绩和认知负荷进行t检验，得到其独立样本t检验表。

从表4得出，记忆测试成绩F=3.785，p=0.056>0.05，所以方差相等。分析假设方差相等所在行的t检验数据，t=-2.144，p=0.036<0.05，所以双向转换组和双向转换+逆转组在记忆测试成绩上有显著性差异。迁移测试成绩F=1.866，p=0.176>0.05，所以方差相等。分析假设方差相等所在行的t检验数据，t=-2.177，p=0.033<0.05，所以双向转换组和双向转换+逆转在迁移测试成绩上有显著性差异。认知负荷F=1.132，p=0.291>0.05，所以方差相等。分析假设方差相等所在行的t检验数据，t=0.156，p=0.876>0.05，所以双向转换和双向转换+逆转在总认知负荷上无显著性差异。

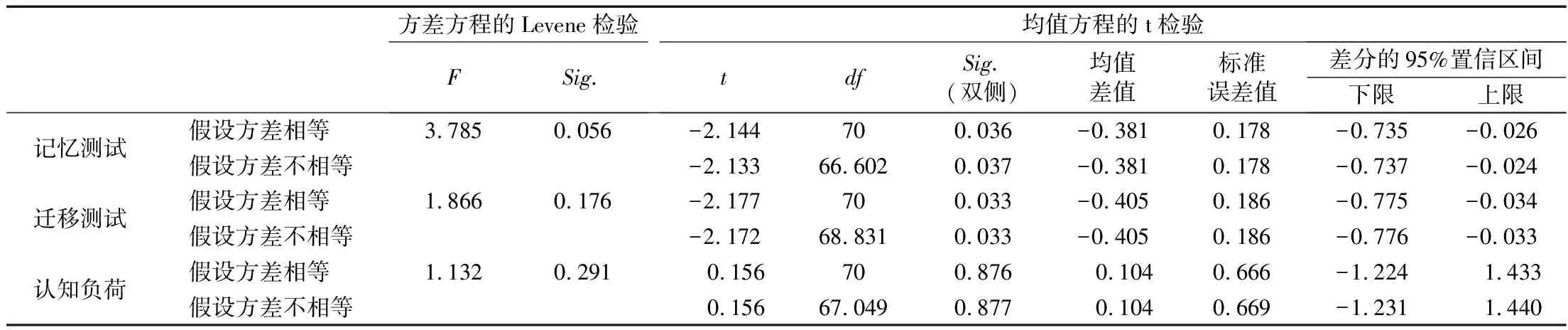
表4 双向转换和双向转换+逆转对学习者学习效果的独立样本t检验

3 讨论

3.1 单项转换对学习者学习效果的影响

学习者在解决和倍问题时存在两种策略，即直接转化策略和问题模型策略。直接转化策略是当学习者面对数学应用题时，首先试图选择问题中的数字和关键词，然后对其进行加工，把数字连起来进行列式，其中强调量的推理，即运算过程，采用这种策略的学习者在一致题型上会得出正确答案，而在不一致题型上将导致解题错误；而问题模型策略是当学习者面对数学应用题时，首先试图理解整个问题情境，然后建立一个心理模型，其中强调指的推理，即问题解决过程中的关系，采用这种策略的学习者即使在不一致的题型上也会成功解题。单向转换为公式即为直接转换策略，单向转换为线段图即为问题模型策略。本研究中，在单项转换中，单项转换为公式组的记忆测试成绩较高，迁移测试成绩较低，单项转换为线段图组的记忆测试成绩较低，迁移测试成绩较高，单向转换为公式组与单向转换为线段图组的记忆测试和迁移测试成绩均存在显著性差异。由于学习者在学习完学习材料后，进行记忆测试时题型一致，此时直接转化策略起到主要作用，而单项转换为公式正训练了学习者此策略，所以单向转换为公式的成绩较高，而进行迁移测试时题型略不一致，此时问题模型策略起主导作用，而单向转换为线段图正训练了学习者此策略，所以单项转换为线段图的成绩较高。

3.2 单向转换与双向转换对学习者学习效果的影响

对学习者来说，有效使用各种表征方式构建数学概念的意义是非常重要的，多种表征方式可以帮助学习者推断问题，促进他们深入思考与探索。本研究中，对于单项转换，单项转换为公式组的记忆测试成绩较高，迁移测试成绩较低，单项转换为线段图组的记忆测试成绩较低，迁移测试成绩较高；而对于双向转换，其记忆测试成绩与单项转换为公式组类似，其迁移成绩与单项转换为线段图组类似，在记忆测试中，双向转换与单向转换为线段图存在显著性差异，与单向转换为公式不存在显著性差异，在迁移测试中，双向转换与单项转换为公式存在显著性差异，与单项转换为线段图不存在显著性差异。这说明，双向转换通过及转换为公式又转换为线段图，经过两种问题表征转换的训练，在记忆测试和迁移测试中均可以达到较好效果，但是经研究发现，双向转换的总认知负荷较高，原因可能是双向转换的任务较多增加了学习者的认知负荷总量。

3.3 双向转换与双向转换+逆转对学习者学习效果的影响

本研究中，双向转换+逆转的记忆测试和迁移测试成绩均显著高于单向转换和双向转换。双向转换+逆转，首先通过双向转换训练学习者两种不同的问题表征转换方式，然后通过逆转，即要求学习者将问题解决过程反向转换为文字，这种反向转换为问题情景的方法，可以训练学习者灵活运用问题的不同表征方式，可以改善学习者对问题解决的理解和表征思维。这也与认知负荷理论一致，双向转换+逆转需要学习者完成更多的任务，因此总认知负荷较高，但是从记忆测试和迁移测试来看，双向转换+逆转的学习效果优于单向转换和双向转换，可以断定双向转换+逆转增加了学习者的相关认知负荷，发挥了积极作用，因此没有产生认知超负荷现象。

4 结语

本研究探讨了在计算机环境下问题表征转换对小学数学学习效果的影响。研究将问题表征理论扩展到复杂情境下的问题解决，结果表明有效的问题表征方式可以促进应用题的学习，丰富了问题表征理论在数学中的应用。同时，本研究设计的多媒体学习资源与传统学习材料相比，增加了提示、交互以及转换思维。尤其是双向转换+逆转使学生对应用题进行了系统的学习，进而深度理解问题，促进了图式的构建和自动化过程。