航天器在轨运行可视化中姿态数据的处理方法
淡 鹏,王 丹,李 力,李代伟
(1.宇航动力学国家重点实验室,陕西 西安 710043;2.西安卫星测控中心,陕西 西安 710043)
0 引言
在航天器飞行试验任务中,地面中心已经越来越多地采用三维可视化技术来表现和展示航天器飞行过程及状态的变化情况(文献[1-3]对比进行了研究)。三维可视化技术的使用为工程技术人员提供了更加直观、更易于理解的飞行过程监视手段,方便了其对任务状态的有效和正确把握,也为飞控决策的制定提供了有力依据,已经成为一些重大任务不可或缺的软件配置。
航天器的三维显示以可视化的形式展示了其位置、姿态、相对关系、部件运动和工作状况等状态信息,其中姿态信息的展示是航天器运行状态表现中非常重要的一部分[4-5]。由于一些任务飞控过程比较复杂,常伴随着航天器的自主机动控制,以及为了减轻操作人员的负担,实际任务中常需要使用实时采集的姿态数据来驱动三维显示,以便更加真实地反映航天器运行状态的变化。但由于设备异常、采集及传输误码、数据预处理异常和操作人员过失等原因,导致实时采集的姿态数据常含有异常或跳变数据。在数据处理中,一般将这种不合理或具有较大误差的数据称为野值。航天器的在轨飞行三维可视化过程中,野值数据的存在容易使显示画面出现跳变,影响实际显示效果,因而在数据使用时首先需要对野值数据予以剔除。同时,为了应对数据中的丢点和跳变点等问题,还需对数据进行必要的插值和平滑处理,以免影响可视化表达的连续性。
对于姿态数据的野值剔除、平滑及插值等问题,可使用的方法较多,较常见的是采用卡尔曼滤波的方法[6-7]来进行野值剔除和平滑处理。但这类方法实现过程相对比较复杂,并且需要较繁琐的滤波参数设置[8]。在一些可视化场合,可能不需要进行此类复杂的运算。为此,本文结合工程实际情况,采用一些较易实现的数值计算方法对三维可视化显示中姿态数据的野值剔除及平滑插值等问题进行了实现。
1 姿态数据及可视化
姿态数据是航天器运行状态的一项重要参数,描述了航天器本体相对基准坐标系的相对关系。对三轴稳定航天器,其姿态信息通常采用3个欧拉角[9-10](俯仰角、偏航角和滚动角)或四元数[11-12]等形式来表示。
航天器在轨运行过程的欧拉角姿态数据一般建立在质心轨道坐标系或当地东南坐标系下,四元数姿态一般相对于惯性系,这几类姿态数据的可视化显示方法可参见文献[4],且欧拉角与四元数2类表达形式之间可方便地进行相互转换[9]。
在三维可视化的实时姿态数据使用过程中,姿态数据由于其不同于星历、轨道等其他类数据的特殊性(转序问题、可能不连续和不同表现形式等),使其预处理较为复杂,下面将针对2类表达形式分别给出解决方法。
2 欧拉角姿态数据的处理
欧拉角是一类常见的姿态表达形式,包含3个角度:滚动角(γ)、偏航角(ψ)和俯仰角(φ)。对其进行可视化数据处理时可对3个角度分量分别进行处理。
2.1 野值剔除
野值数据通常情况下表现为脱离大多数数据点变化趋势,幅值相差悬殊,点数较少。一般情形下,对欧拉角野值数据的粗处理可采用以下几种方法。
2.1.1 粗大野值的阈值剔除
给定姿态数据某测量分量ν的阈值范围[νmin,νmax](例如[-360°,360°]角度范围),当测量数据不在该范围时直接剔除,这样可将明显的错误数据剔掉,减少后续处理的压力。
阈值剔除是数据处理的第一步,但在其使用中需合理设置阈值范围,不能设置过小以免将某些正常数据剔掉,使用时可根据理论飞行状态及其变化情况进行设置。
2.1.2 差分检测法
考虑到航天器姿态运动过程中,姿态角速度范围是有限的,因而可通过前后两点姿态角变化与姿态角速度的相关性比较来判定野值。设角速度某分量的阈值范围为[ωmin,ωmax](可为负数),相应姿态角分量前后两点测量值为ν1,ν2,两点间时间间隔为Δt,则应满足ωmin·Δt≤ν2-ν1≤ωmax·Δt,否则,可认为后点为野值(正常往后递推剔野时,非起步判断过程)。
实际使用时,角速度阈值取值也应适当放大,以免将合理数据剔除。另外,t应进行适当的限定,即当t>tmaxin(tmaxin为连续判断的时间间隔最大允许值)时,认为数据中断,应重新进行野值的起步判断。
2.1.3 预测值管道剔除法
基于一定时间内的观测数据,可采用多项式拟合、滤波等方法预测出下一时刻的观测数据,若实际测量值与预测值偏差较大,则可被视为野值。偏差比较采用阈值比较方式进行,此即预测值管道剔除法。管道法剔除递推剔除示意图如图1所示。

图1 管道法剔除递推剔除示意
设由前n个数据预测出的下一测量数据为νF,实测量为ν,管道最大值为Δνmax,则当νF-ν>Δνmax时视为野值。
考虑到可能跨越±180°的情况,上式修改为:Trans(νF-ν)>Δνmax(此处Trans表示规约到±180°范围内的转换函数)。
上面几种方法只是对粗大型野值的处理,实际计算中还需结合角度数据的平滑过程进行进一步处理。
2.2 欧拉角插值及补点处理
对于被当做野值剔除掉的数据点,如不进行数据补齐,就可能造成姿态显示时画面跳动,为此必须进行补点处理。同时,在一些平滑性要求更高的场合,可能需要一秒多帧显示,此时就可能需要将数据插值为每秒多点。
工程上常采用的补点处理方法有2类:一类是进行数据插值;另一类是采用预测值代替(可采用多项式拟合预测、滤波预测等)。
欧拉角的插值主要采用2点线性插值、多点拉格朗日插值和样条插值等方法。
由于工程计算中欧拉角一般被限定在一定范围内(如[-180°,180°])变化,这就造成角度数据在形式上是不连续的(尽管实际几何关系可能连续),如值在±180°前后的变化过程[10]。因而插值时需要对其做连续性处理,方法为:
方法1:采用加减360°的方法,将数据规整为连续型数列;
方法2:三角函数方法,改用三角函数进行插值,然后反解出相应角度。
2.3 多项式最小二乘平滑处理
多项式拟合最小二乘估计处理是一种兼具预测、平滑及剔野功能的方法。
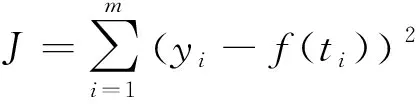
在欧拉角的多项式最小二乘处理使用前,首先需要采用前面的方法进行粗大型野值处理,以剔除掉明显超出测量范围的大野值。然后对数据点使用多项式f(t)进行平滑。可以固定每次平滑的数据点数,以保证算法运算速度不会由于数据的增多而减慢。在一次拟合后,计算出样本方差σ,即
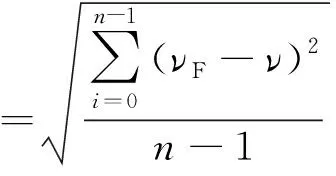
式中,νF为ν的预测值。
然后,计算出每个观测数据点yi的偏差Ei=yi-f(ti),进而对其进行方差检验(kσ检验,k为倍数,如取3),剔除掉本次迭代计算的野值。
接下来重新进行拟合迭代计算,直到满足收敛条件为止,收敛条件取为:
① 迭代次数少于给定值;
② 前后2次计算的拟合值相差小于某给定小量(如取1×10-5)。
需要注意的是,该方法的剔野效果有限,因而主要用来进行拟合预测、数据平滑计算以及被剔除点的补点计算等方面。
2.4 起步处理
在数据中断一定时间后,或首次接收到数据时,需进行起步处理。起步处理的好坏直接影响了后续的差分剔野、拟合值管道剔野以及平滑处理的效果。故此处可采用多点数据起步。
首先进行粗大野值的阈值剔除,然后计算前后两点的差分姿态角变化率。当不满足限制条件ωmin·Δt≤ν2-ν1≤ωmax·Δt时,将ν2点舍弃或将其之前的数据全部舍弃(尽量保留新数据,与前面正常递推过程差分剔野不同),并继续积攒数据,重新进行起步成功判断。该方法的使用需要给定合理的起步时ωmin,ωmax范围。
2.5 滑窗计算
在多点数据拟合预测、多项式平滑中,可采用多点数据滑窗计算方法。计算时,需注意数据的中断情况,当前后两点时标差超过一定时间(如50 s)时,认为数据中断,需重新起步处理。
同时,当连续多帧(或一定时间段)数据均被当做野值剔除时,可认为当前剔野参数设置不合理,已经适应不了当前姿态的变化(即管道过小),需对剔野门限放大(可采用连续多点角变化率平均值的多倍进行自适应计算,并进行适当限幅)。
3 四元数姿态数据的处理
欧拉角姿态存在旋转不唯一、有转序设定问题、旋转不均匀以及运动方程存在奇点[10,13]等缺点。因而在角度变化较大的姿态计算中,常采用另一类表达形式,即四元数数据。
3.1 剔野处理
四元数为一个四维向量,其姿态旋转轴由四元数矢部决定,旋转角度由标部决定[14]。
设航天器在惯性系下的单位姿态四元数qm的4个分量为qm0,qm1,qm2,qm3,其中qm0为四元数的标部;qm1,qm2,qm3为矢部。则野值剔除可通过以下步骤进行:
① 计算四元数的模

若模不为1,则判定为异常值。用公式表示为:
qm-1>η(η为比较阈值,如取0.01)。
② 计算四元数矢部的模,若为0(可取为小于1×10-6),则说明旋转轴数据异常,将该数据剔除。
③ 计算前一个接收到的正常姿态数据qt-1到当前四元数qt的增量四元数(或称作机动四元数)Δq:

计算增量四元数对应的转角Δα:
Δα=2arccos(Δq[0]),
式中,Δq[0]表示取Δq的标部。
将此转角与角速度阈值进行比较,设时间增量为Δt,则比较式为ωmin·Δt≤Δα≤ωmax·Δt,若不在此范围,说明连续2个姿态数据的变化超出正常值,可判定当前四元数为异常值。
④ 序列数据的角速度拟合判断
对一时间连续未发生中断的数据序列,由上面计算的每一点与前一点的转角计算其角速度,可得到一角速度序列,可将最后一点(最新点)计算的角速度与序列多项式拟合值进行阈值比较,判断是否要将最新点剔除,剔除后用插值结果作为输出(但原始测量值仍参与下一点数据剃野判断,以减少机动时的误判)。
3.2 插值计算
四元数姿态插值的一种简易算法是先将其转换为欧拉角姿态再进行插值。但这种算法最大缺陷在于若转序选择不好,可能导致欧拉角的奇异问题的发生[9,15],从而放弃了四元数的优越性,且该方法会导致计算量增大,因而不推荐使用。
四元数插值[16]最简单的方法是进行线性插值,对于2个四元数q1,q2,其线性插值公式为:
qt=q1+λ·(q2-q1),0≤λ≤1,
式中,λ为q1变换到q2间的插值参数。插值计算中需注意的是:q1,q2应为单位四元数,且插值后的值也应转换为单位四元数,将公式修改为:

该算法计算过程简单,但缺点在于忽略了旋转的球面特性,其插值过程不是匀速进行的,有加速和减速过程。为此,本文主要采用球面线性插值方法。
Ken Shoemaker[17]采用单位球面上大段圆弧类比欧式空间中直线的插值方法,提出了2个姿态间的球面线性插值(Spherical Linear Interpolation,Slerp插值),其最初是为了模拟3D旋转在四元数插值(Quaternion Interpolation)基础上改进的方法,当给定末端且在0~1之间插值时,Slerp指的是沿着单位半径大圆的常速运动。
给定t时刻左右两端的四元数q1,q2(均为单位四元数,q1分量为q10,q11,q12,q13;q2分量为q20,q21,q22,q23),对t时刻姿态(设为qλ)进行Slerp插值,基本计算原理如图2所示。

图2 Slerp插值原理示意
由图2中几何关系可推导出插值公式为:

式中,λ为插值参数,且λ∈[0,1];θ为2个四元数之间的夹角:
θ= arccos(q1·q2)=
arccos(q10q20+q11q21+q12q22+q13q23)。
4 实验结果
对某航天器姿态机动过程中某段时间内的实测姿态数据进行剔野[18-19]和平滑[20]处理,处理前后的偏航角曲线如图3所示。

图3 某段实测数据处理前后对比
从图3中可见,大多数野值点均被有效剔除,且处理后的曲线较平滑。
原型软件(采用VC与OpenGL编写)对某深空探测器四元数姿态可视化效果如图4所示。

图4 原型软件对探测器飞行过程姿态可视化效果
5 结束语
对航天器可视化中姿态数据的处理方法进行了阐述,实验结果表明该方法是可行的。应该看到,野值剔除是一个比较困难的命题,各种处理方法均有一定的适用范围,使用中需根据航天器运动情况适时调整参数才能得到更好的结果。下一步将重点在姿态数据的滤波处理方法上进行研究。

