一种基于双树复小波变换的图像去噪算法
毕思文,陈 浩,帅 通,李 娜
(1.中国电子科技集团公司航天信息应用技术重点实验室,河北 石家庄 050081;2.中国科学院遥感与数字地球研究所,北京100101)
0 引言
数字图像在成像和传输过程中,经常会受到各种各样的噪声干扰[1]。为了使后期的图像理解和图像分割等操作更加有效,需要对受到噪声干扰的图像进行处理。
在图像去噪方面,人们提出了许多图像去噪算法,文献[2] 提出基于Cycle Spinning的图像自适应阈值去噪方法,该方法提高了去噪图像峰值信噪比(PSNR),降低了均方误差(MSE),去噪图像清晰,获得较好的视觉效果。 文献[3]通过平稳小波变换对图像进行小波分解,对于子图像的高频区域进行阈值分割和双边滤波,利用平稳小波更好的冗余性和平稳不变性,更好地去除了SAR图像的相干斑噪声,实验表明这种改进的去噪方法对SAR图像的相干斑噪声有很好的抑制效果。文献[4]提出了一种新方法来滤除图像中的云雾,结果表明,该算法优于传统滤波方法,且对于薄云图像效果更佳。 文献[5]在经典小波阈值去噪算法的基础上改进了阈值函数,提出了一种新的小波阈值去噪算法,实验结果表明该算法提高了信号特征的可分离性,具有较高的实用价值。
小波分析是为了弥补短时傅里叶变换的不足而发展起来的一门应用数学学科[6]。基于小波分析的去噪方法最早由Mallat提出,他在1992年建立了小波变换快速算法,并将其运用在信号和图像的分解和重构中[7]。1999年,Kingsbury提出了双树复小波变换(Dual Tree Complex Wavelet Transform,DTCWT),具有平移不变性,提供了6个方向的信息,因而具有较好的方向性和精确的相空间信息[8]。在DTCWT提出以后,有很多学者在基于双树复小波的去噪方法方面做了大量研究。文献[9]提出了一种基于双树复小波变换和形态滤波的去噪算法。文献[10]提出了一种基于非下采样双树复小波域的图像去噪算法,实验表明该算法比经典算法提高了一定的峰值信噪比,且有良好的视觉效果,较好地保持了图像中的纹理特征。文献[11]综合考虑空域滤波和变换域滤波的优点,提出了一种基于DTCWT和自适应窗的图像去噪算法,将双树复小波变化和自适应椭圆窗口滤波相结合,考虑了小波分解的不同子带具有不同的能量方向,以椭圆方向窗作为领域,获得了比较好的去噪效果。但文献[11]中使用的椭圆窗作为邻域,系数估计时均需要采用椭圆模板进行匹配,所以算法运行时间较长、复杂度略高。
本文借鉴多量子位量子叠加态的测量坍缩原理,根据双树复小波较好的方向特性,以坍缩后的状态作为邻域计算小波系数方差,利用双树复小波提供的方向信息和量子叠加态的测量坍缩原理运用到图像去噪中进一步去噪。实验结果表明,本文提出的图像去噪算法与文献[11]的图像去噪方法相比,去噪性能得到改善,运行时间明显提升。
1 双树复小波变换
DTCWT变换可以通过两对滤波器组同时作用在输入数据上来实现。复小波可以表示为:
ψ(t)=ψr(t)+jψi(t),
(1)
式中,Ψr(t)表示复小波的实部;Ψi(t)表示复小波的虚部。Ψr(t),Ψi(t)都是实函数,因此,DTCWT可以表示为2个独立的实小波变换,包含了2个平行的小波树:树a和树b。DTCWT分解示意图如图1所示,树a和树b的叠加滤波器组分别表示复数小波变换的实部和虚部,↓2表示隔点采样[12]。为了保证滤波器的冲击响应对应于复小波变换系数的实部和虚部,采用2棵树的滤波器长度分别为奇数和偶数且是线性相位。基本原理就是利用一对实滤波树,同时对输入信号进行分解,产生小波系数的实部和虚部。

图1 DT-CWT分解示意
二维的双树复小波实部与虚部小波系数能提取±15°,±45°,±75°六个方向的高频信息,相对离散小波变换(Discrete Wavelet Transform,DWT)具有近似平移不变性、多方向选择性、更高定位精度和计算效率等优点[13]。相比之下,DWT在每个尺度上有3个小波子带,只能反映出水平数竖直和对角方向。二维DT-CWT在空间域和在2-D平面内(理想化的)表示出具有6个不同的角度DT-CWT小波如图2所示。

图2 DT-CWT的脉冲响应及在二维平面等效
2 量子叠加态的测量坍缩原理
2.1 态叠加原理
若|Ψ1〉是Hilbert空间中的一个矢量,|Ψ2〉是另外一个矢量,由态叠加原理可知:
|Ψ〉=c1|Ψ1〉+c2|Ψ2〉,
(2)
也是Hilbert空间中的一个矢量。其中c1,c2分别是状态|Ψ1〉|Ψ2〉的概率幅。且满足归一化条件:
c12+c22=1。
(3)
所以若量子系统处在|Ψ1〉和|Ψ2〉描述态中,则式(2)的线性叠加态|Ψ〉也是该系统的一个可能态,这就是量子力学的态叠加原理[14]。量子比特[15](qubit)是量子信息理论中的一个重要概念,对一个具有2个基态的双态量子系统[16]。若将2个基态分别记为|0〉和|1〉,记量子比特为:
|Ψq〉=a|0〉+b|1〉。
(4)

|Ψ〉= |Ψ(1)〉 |Ψ(2)〉…|Ψ(n)〉=




(5)
式中,|i〉表示第i个基态;ωi为基态|i〉的概率幅,满足归一化条件:
(6)
2.2 量子叠加态的测量坍缩
由量子力学第三假设可知,设测量算子由{Mm}描述,测量前量子系统的最新状态是|Ψ〉,则测量后系统的状态为[17]:
(7)
为了更好地理解量子测量坍缩原理,举例如下:对于一个4×4的叠加态结构元素(归一化以后),若另取一个4×4的阵列,将阵列中边缘的最大的2个灰度值取为1,其余取值为0,则得到{Mm},对应|iM〉=|0001000000001000〉,若用此测量算子Mm=|0001000000001000〉〈00010000000010000|对邻域图像进行测量,则邻域图像将坍缩到基态|iM〉,如图3所示。

图3 测量前和测量坍缩以后
由于图像中不同点之间领域的特征不一样,所以在不同移动点所得到的测量算子和测量后的坍缩态也不同[18]。以上就是双树复小波变换以后,计算+45°方向邻域,其他方向类似。
3 本文提出的改进算法
3.1 算法模型
假设原始图像被均值为0,方差为σ2的高斯白噪声污染,当在小波域通过小波变换系数进行去噪后采用以下模型:
Y(i,j)=X(i,j)+N(i,j),
(8)
式中,Y(i,j)为含噪小波系数;X(i,j)为待估计的干净小波系数;N(i,j)为噪声小波系数。采用MAP预估器可表示为:

(9)
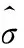

(10)
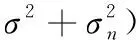

(11)
将式(10)带入式(9),并对其进行求导,令其导数为零可得:

(12)
式中,M为邻域N中系数的个数。若已知图像信号的方差分布,那么由最大后验概率估计(Maximum A Posterior,MAP)可得:

(13)
式中,fσ(σ2)为图像信号的方差分布。由式(13)推导可得:

(14)
3.2 算法流程
根据以上算法模型,本文去噪算法步骤如下:
① 对图像进行双树复小波变换;
② 利用量子态叠加的测量坍缩原理,以4×4的阵列测量分解层;
③ 以坍缩后的邻域用式(8)和式(11)计算λ;
④ 重复步骤②,然后利用式(13)估计双树复小波系数的方差;
⑤ 利用式(8)得到去噪以后的系数;
⑥ 双树复小波反变换,得到去噪后的图像。
4 实验验证与分析
为了验证本文所提算法的有效性,实验中选用标准的512×512大小的8位灰度图像作为实验对象。实验中,假定用均值为0、标准差分别为10,15,20高斯白噪声污染,对测试图像进行4层的下采样双树复小波分解。在文献[19]中指出,对包含了高斯噪声的图像进行3级小波分析,并对高斯噪声小波系数的分布情况进行了统计分析,发现大约有96%的噪声系数分布在最外2层的细尺度子带中[20]。因此,对第二、第三和第四分解层,采用利用量子态叠加测量坍缩原理,选取4×4的阵列中四周最大的2个值取值为1,其他的取为0,以此作为双树复小波分解以后的主方向,并且在此方向上作为系数估计的邻域。将本文所提算法和文献[11]做比较(PSNR 和运行时间)。
实验效果图和文献[11]的数据对比结果如图4和图5所示。

图4 2种去噪算法结果比较(Lena)

图5 2种算法去噪结果比较(Barbara)
表 1 2种不同去噪方法得到的PSNR值比较

算法LenaBarbara1015202510152025平均运行时间/s文献[11]算法30.528.627.325.633.230.228.826.27.6本文算法30.828.627.525.833.330.428.926.62.1
通过表1可以看出,利用本文所提算法得到的PSNR值比文献[11]要略高,从处理以后的效果图来看,本文所提算法有相同的抑制噪声的能力,但由于本文所提算法将量子态叠加的测量坍缩原理与双树复小波变换相结合,将坍缩状态作为计算子带的方向窗,既利用了双树复小波变换的方向特性,同时避免了文献[11]中每次系数估计时都要进行模板匹配的操作,因此,在运行时间上比文献[11]有很大的提高。
5 结束语
本文将双树复小波变换和量子态叠加的测量坍缩原理相结合,利用双树复小波变换较好的方向特性和叠加态结构元素在不同位置坍缩为不同大小和形状的属性,避免了方形结构元素所不具备的方向性特性和椭圆结构元素带来的复杂性。通过实验发现,将量子力学中的理论运用到图像去噪中,大大提升了运行速度并验证了本文算法的有效性。该算法虽然在运行时间上相对于其他方法有较高提升,但是在评价指标PSNR数据上的提高并不明显,需要对算法进行优化改进,仍有较大的提升空间。

