基于SIM仿真平台的载人登月软着陆任务研究

周晚萌，李海阳，王 华，黄海兵，李云飞

(1.国防科技大学空天科学学院应用力学系，长沙410073；2.长沙翔宇信息科技有限公司，长沙410073；3.上海宇航系统工程研究所，上海201100)

1 引言

近年来，随着国际空间站服役期限的临近，原空间站合作方开始共同提出了一项关于国际环月空间站的研究计划，截止于2016年10月，研究方案已基本明确。同时，我国也在开展围绕环月空间站的载人探月系列任务，以充分继承我国在近地空间站建设的经验优势，实现月球的长期探测。载人登月系统复杂，很难由某家单位独立实现全任务仿真，必须利用仿真平台进行多家任务单位的模型集成。载人登月软着陆任务仿真系统主要包括飞行任务仿真单元、飞行任务规划单元、飞行任务评估单元和可视化单元。

飞行任务仿真单元对月面着陆器和上升飞行器组合体在下降和返回过程进行动力学仿真。再入动力学模型一般采用速度、航迹角以及偏航角描述速度状态，但月面软着陆的最终速度为0，求解过程中会出现奇异[1]，为此飞行任务仿真单元直接利用速度分量来描述动力学方程中的速度状态。飞行任务规划单元主要针对定点着陆和月面上升问题展开研究。这类问题均可以归结为终端时间可变的燃料最优控制问题，目前主要分为直接法和间接法两类[2]。间接法将通过极大值原理建立协调方程与状态方程联立求解[3-4]，但该方法对协调变量初值要求较高[5]，同时软着陆过程中的约束也加大了方程的推导难度[6]，因此国内外主要采用直接法对此类问题展开研究。直接法具有更强的鲁棒性和适应性[7]，直接法中的直接打靶法将控制量离散，并将问题转化为多设计参数的非线性规划问题，利用SQP算法或智能优化算法来求解[8-10]，主要问题是直接法为了降低求解难度，忽略了月球自转，因此并未引入着陆点的位置约束。另外，也有学者利用直接法中的正交配点法求解月球软着陆问题[11-13]。

美国、俄罗斯/苏联、欧洲和日本多年来致力于仿真平台的构建，并在地面试验验证中起到了非常重要的作用[14-15]。我国很多高校和研究机构在相关领域也搭建了各具特色的仿真平台，如吴魁等[16]采用分布式仿真架构提出了运载火箭总体设计仿真评估平台；孙福煜等[17]设计了基于高层体系架构(High Level Architecture，HLA)的分布仿真环境KD-HLA；卿杜政等[18]提出了基于HLA的SSS-RTI系统。

本文采用共享内存与HLA相结合的机制与可视化组装技术，搭建了从建模、调试、组装到仿真的全生命周期的数字化载人登月任务仿真平台(Simulation Management Platform，SIM)。 在 SIM平台的基础上建立由飞行任务规划单元、飞行任务仿真单元、飞行任务评估单元和可视化单元组成的载人登月软着陆任务仿真系统。利用该系统进行软着陆飞行任务规划算法的验证和仿真评估，其中飞行任务规划单元采用变网格Radau伪谱法实现，以期在应急条件约束[19]下，可以同时保证计算精度和收敛效率。

2 飞行任务仿真单元

2.1 动力学模型

如图1所示，飞行仿真单元采用月面着陆坐标系o-xyz建立动力学模型，着陆坐标系属于动坐标系，具体定义为z轴沿飞行器矢径方向，xoy平面为当地水平面，x轴与当地正北方向存在一个偏角γ，且保持不变，y轴由右手定则确定。推力器的推力方向可以由方位角β和高低角α来确定。高低角定义为推力矢量与当地水平面的夹角，范围为 [-90°，90°]， 正值表示在水平面上方，负值表示在水平面下方。方位角定义为推力水平面投影矢量与着陆坐标系的夹角，范围是 [0 °，360°]。 为获得完整的动力学模型，首先需要确定月心J2000坐标系O-XYZ、月心赤道固联坐标系O-X1Y1Z1与月面着陆坐标系三者之间的转换关系。仅考虑月球自转影响，O-XYZ与O-X1Y1Z1之间相对角速度为月球自转角速度ωL，O-X1Y1Z1与o-xyz的角速度为Ω，需要先绕Z1轴转动一个经度角λ，再绕新的Y1轴转动90°-φ，φ为纬度角，最后绕新的Z1轴转动180°-γ。

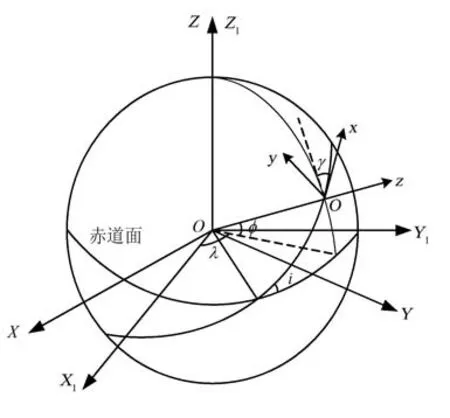
图1 月面着陆坐标系示意图Fig.1 Coordinate systems in lunar soft-landing

月球自转角速度ωL、o-xyz相对于O-X1Y1Z1的角速度为Ω，动力学模型的o-xyz分量可以表示为式(1)[20]。

其中，质心相对于O-X1Y1Z1的速度在o-xyz坐标系的分量为(u，v，w)，r为着陆器矢径，T为推力幅值，m为质量，μL为月球引力常数。另外，全过程燃料消耗外加质量方程为式(2)。

其中，Isp表示发动机比冲，g0表示地球重力加速度。为提高轨迹优化精度，将距离单位DU，时间单位TU，质量单位MU等单位量级归一化，具体定义 1 DU＝1RL，1 TU ＝，1 MU＝1m0。 其中，RL为月球半径，m0为组合体初始质量。

2.2 边界条件及过程约束

软着陆的边界条件包括位置和速度约束，一种位置约束为式(3)。

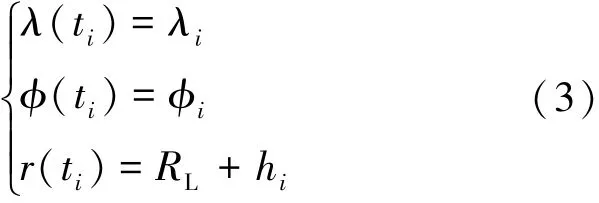
其中，h为距月面高度，i＝0、f表示初始和终端状态。速度的初始约束表示为式(4)。

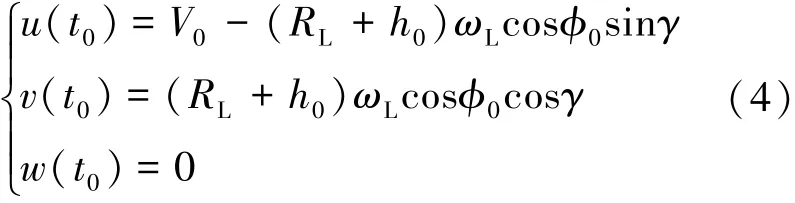
其中，V0表示初始轨道的速度，由于组合体动力下降之前处于远月点高度为环月轨道高度hLLO、近月点高度为h0的椭圆轨道，并从近月点开始降轨，终端约束为u(tf)＝0，v(tf)＝0，w(tf)＝0。

在动力下降过程中还要考虑到其他的过程约束，发动机推力以及转角的限制为式(5)。

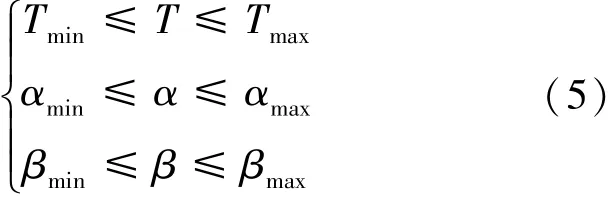
航天员承受过载限制为式(6)。

其中，过载n可以用最大值的情况来直接表示为n＝T/m＋μL/r2。

要满足应急返回的条件，必须使软着陆过程中的速度分量以及径向与切向速度比值不能超过限制，如式(7)所示。

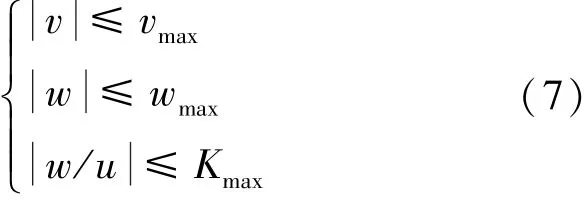
3 飞行任务规划单元

按照配点的选取方式不同，可以将伪谱法分为Legendre、Gauss以及Radau伪谱法，这里采用Radau伪谱法作为基础，并进一步动态划分网格。

Radau配点为-1，1( ]上多项式gK(τ)的根，称为Legendre-Gauss-Radau(LGR)点，多项式表示为式(8)。

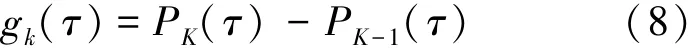
其中，PK(τ)为K阶勒让德多项式，可表示为式(9)。

将时间变量归一化为τ-∈ [-1，1]，以τ-＝-1和K个LGR点作为插值节点，对状态变量进行K阶拉格朗日插值，如式(10)所示。

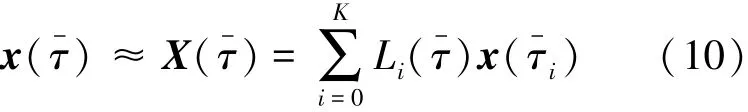
其中，Li(τ-)为拉格朗日插值基函数，表示为式(11)。

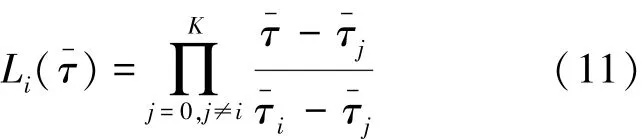
由式(10)可知，插值函数在节点处的真实值等于近似值，即(i＝0，…K)。同理，可得控制变量的插值结果如式(12)所示。

其中，为拉格朗日插值基函数，表示为式(13)。

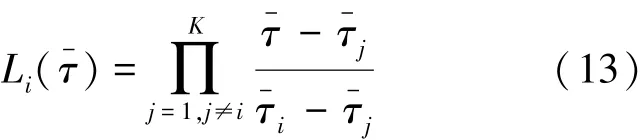
离散化后在LGR点上的状态微分，可以表示为式(14)。

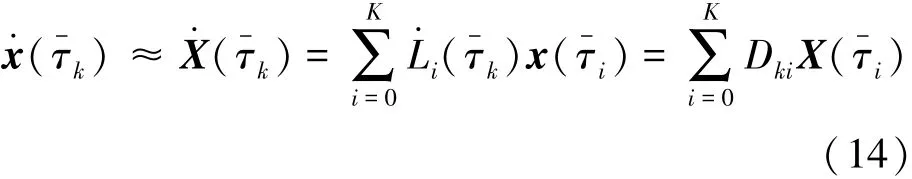
其中，k＝1，…，K，D∈R RK×(K＋1)为微分矩阵，与优化问题本身无关，只与LGR点的选取有关，为拉格朗日插值基函数的微分，表达式为式(15)。

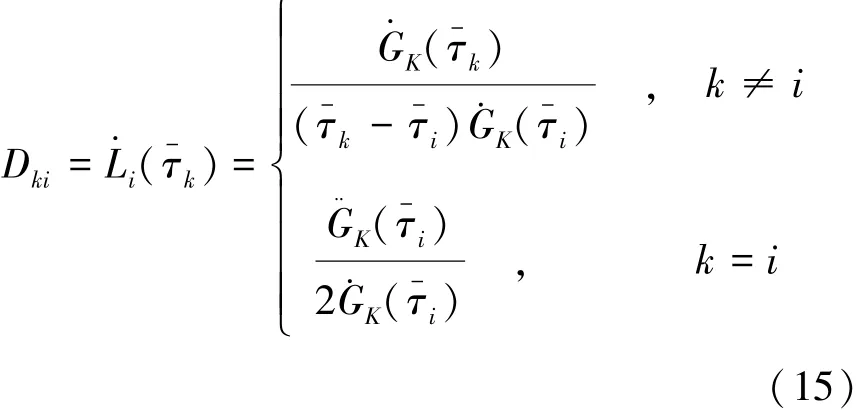
其中，Gk(τ)＝(1＋τ)gk(τ)。 由上述的状态微分近似，在LGR点(配点)上对动力学微分方程进行配置，如式(16)所示。

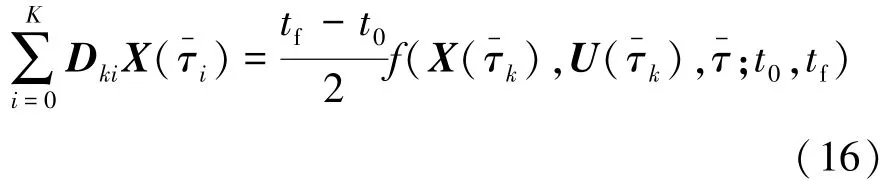
系统的终端状态可表示为式(17)。

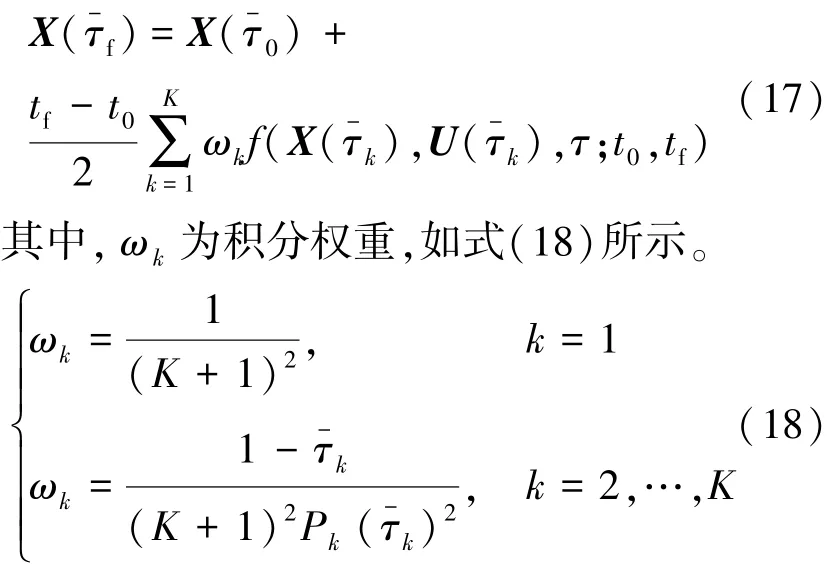
最后，对性能指标J＝Φ(X0，t0，Xf，tf)＋进行处理，对其中的拉格朗日型指标采用高斯求积进行离散，可得式(19)。

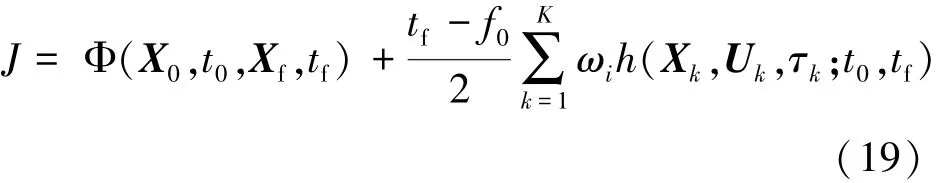
伪谱法计算过程中，配点并非全局插值，而是将求解区间划分为多个小区间，每个区间内具有多个插值，一般的伪谱法在每个区间内以相同的阶数对状态和控制变量进行插值，而变网格自适应则要求通过式(16)计算子区间残差， 判断是否需要进一步加密网格或调整插值阶数。若在容许误差范围内，则停止迭代计算，否则需要自适应调整。网格细化的判据为式(20)。

其中，为第k个区间内的最大曲率和平均曲率，区间内第s个点的曲率计算公式为式(21)。

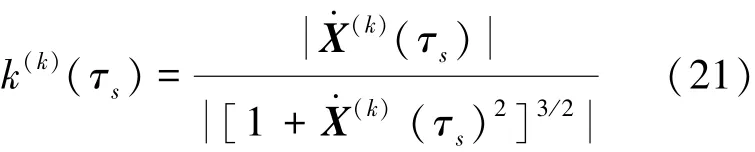
若r(k)超过给定的最大限度，则需要按式(22)加密网格；否则，需按式(23)提高插件阶数。

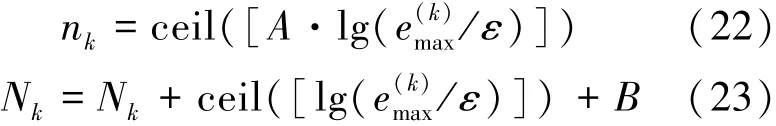
式中，A、B为调整参数。

在每次迭代中，网格的划分和插值阶的选取都不断趋于合理，在保证计算精度和速度的条件下，增强了对不连续和状态量快变问题的优化计算能力。

4 仿真系统设计

在硬件平台的基础上，构建应用层、工具层、中间件层、基础资源库层4层结构的软件环境。应用层针对特定任务(如载人登月软着陆任务)开发仿真应用，工具层、中间件层、基础资源库层和硬件层构成实验室通用的仿真运行环境，如图2所示。工具层中的仿真运行支撑平台SIM作为载人航天任务预研仿真论证的主要平台。

4.1 SIM平台架构设计

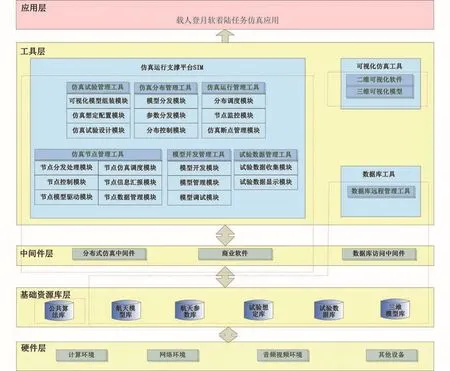
图2 SIM平台仿真运行环境架构Fig.2 Structure of simulation environment in SIM platform

SIM平台包括仿真管理软件SIM、仿真客户端软件SIM.Client、仿真数据管理软件SIM.Data、仿真模型生成软件SIM.Creator、仿真模型调试软件SIM.Debug等，如图3所示。为了解决传统HLA仿真完全依赖网络交互数据，难以适应高频度数据交互要求的难题，SIM仿真平台采用高性能HLA/SharedMemory两层交互机制，在同一计算机上的模型之间采用SharedMemory交互机制，在不同计算机上的模型之间采用HLA交互机制，极大提高了仿真速度。

在SIM平台中，支持仿真模型框架生成(SIM.Creator)、仿真模型调试(SIM.Debug)、仿真模型集中管理(SIM/SIM.Client)以及数据管理(SIM.Data)。

平台采用“分布计算、集中管理”思想，在管理节点集中进行仿真模型管理和仿真试验管理。仿真试验管理形成仿真想定后，由仿真分布管理工具根据仿真想定将各仿真模型和模型参数分布至相应计算节点，并将模型启动、关闭等操作集中在管理节点进行，如图4所示。

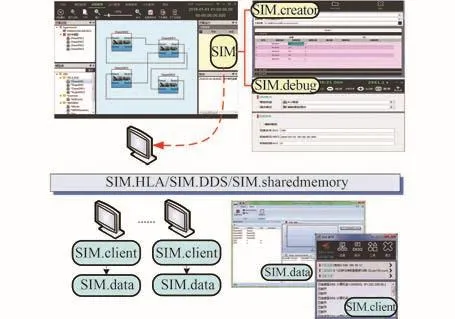
图3 SIM平台组成Fig.3 Composition of SIM platform

4.2 任务仿真系统设计

载人登月软着陆任务仿真系统采用SIM作为底层平台，整个系统分为4个单元：飞行任务规划单元、飞行任务仿真单元、任务评估单元和可视化单元。

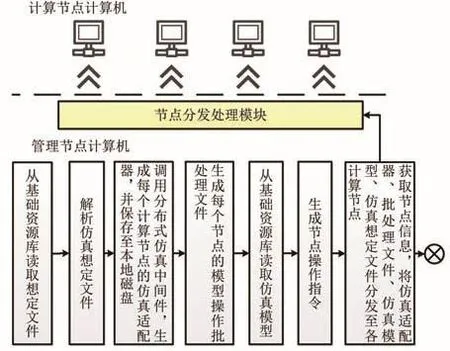
图4 仿真分布管理模型分发运行原理图Fig.4 Schematic diagram of model operation and dispersal in simulation distribution management

在对载人登月软着陆任务仿真之前，需通过飞行任务规划单元按照飞行任务要求，对载人登月软着陆涉及的软着陆轨迹进行规划，并将初始轨道、变轨控制参数等规划结果作为初始条件的一部分发送至飞行任务仿真单元。通过SIM.Creator自动生成月面着陆器飞行仿真单元、任务评估单元以及可视化单元的模型框架，建立仿真模型。利用SIM.Debug独立于仿真平台进行单节点调试并录入到SIM。SIM采用可视化的树状结构管理各节点的录入模型，通过拖拽、连续等方式实现试验系统的图形化组装。集中配置试验参数和仿真模型，完成仿真系统的设计。SIM平台真正实现了贯穿仿真系统的全生命周期过程，在建模、调试运行、仿真评估及态势展现的各个阶段提供全方位支持。根据飞行任务规划结果，完成飞行任务仿真推演，实现软着陆全过程的仿真模拟，实时将飞行器与相关设备的状态与参数输出至飞行任务评估单元和可视化单元，完成测控通信、光照能源等专项评估以及可视化展示，如图5所示。

5 仿真分析

将搭建好的软着陆飞行任务规划单元和飞行任务仿真单元分布部署在不同的仿真节点上。节点采用的处理器为3.4 GHz Intel Core i7-6700，8GBRAM，操作系统为Windows7。

采用算例的具体方案为：组合体飞行器从环月极轨道出发，进入高度为15 km×110 km的椭圆轨道，无动力滑行至近月点后，开始进行动力下降。

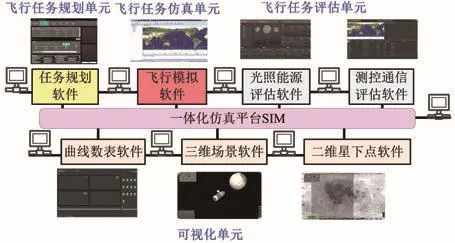
图5 载人登月软着陆任务仿真系统架构图Fig.5 Architecture of manned lunar soft-landing simulation system

软着陆过程中的推力最小值Tmin为4.5 kN，最大值Tmax为45 kN。 高低角范围-30°～30°，方位角范围160°～200°。 最大过载nmax为1，vmax为50 m/s，wmax为45 m/s，Kmax为0.3。

变网格Radau伪谱法的各子区间的配点个数取值范围是4～10，迭代的最大代数为20，容许误差为10-5。按照表1的数据配置各单元模型，开始运行仿真，同时记录Gauss伪谱法和变网格Radau伪谱法最终的燃料消耗与计算耗时，结果如表2所示。

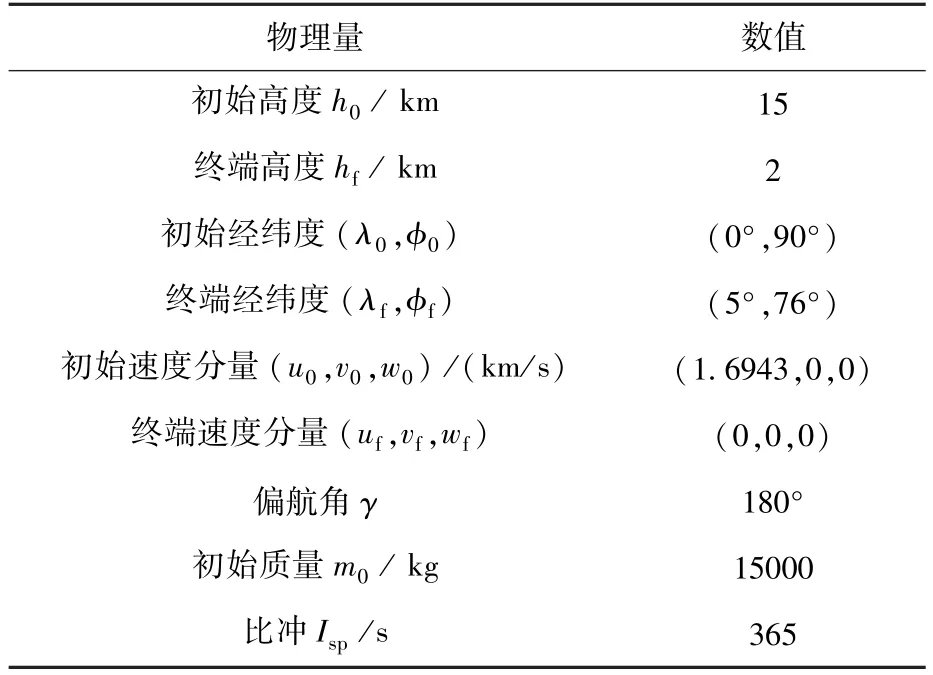
表1 仿真算例参数配置Table 1 Parameters of simulation example

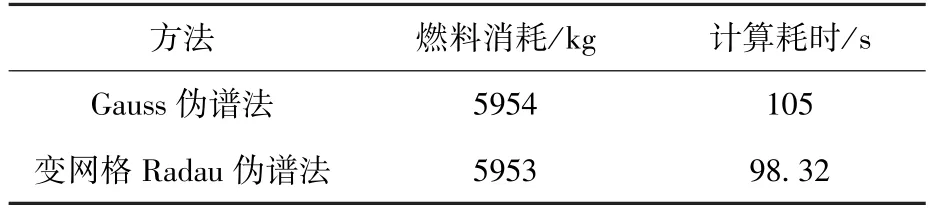
表2 仿真结果对比Table 2 Comparison of simulation results

由此，可知本文算法规划结果燃料为5953 kg，与Gauss伪谱法相比，燃料消耗更少。对比计算耗时可以发现变网格Radau伪谱法仅为98.32 s，低于Gauss伪谱法的平均计算耗时。由于变网格的划分以及插值阶数的改变仅发生在局部网格而非全局过程，因此所提方法在保证计算结果的同时还可以获得高于传统Gauss伪谱法的计算效率。飞行过程中的推力方向如图6所示。

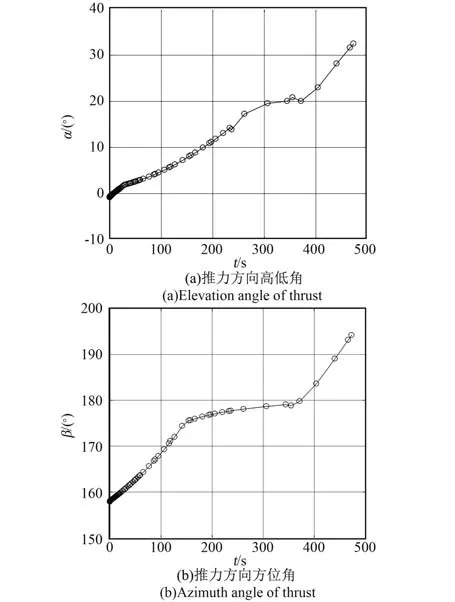
图6 推力方向曲线Fig.6 Directions of the thrust

由图中的仿真结果可知，推力的方位角为钝角，并且位于水平面上方，始终保持纵向和法向的减速。在中间一段平稳的飞行段，推力方向约为180°并持续了200 s左右的时间。软着陆过程中的推力幅值如图7所示。

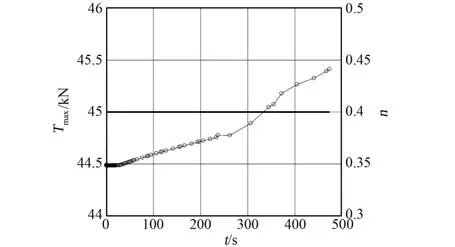
图7 推力幅值与过载大小Fig.7 Thrust amplitude vs.overloads

图7 中左边y轴展示了推力幅值的大小，右边y轴展示了整个过程的过载大小。从图中可知，全过程推力器始终处于开机状态，推力恒定为最大值，过载在约束范围内不断升高。软着陆过程中的剩余质量如图8所示，速度分量如图9所示。

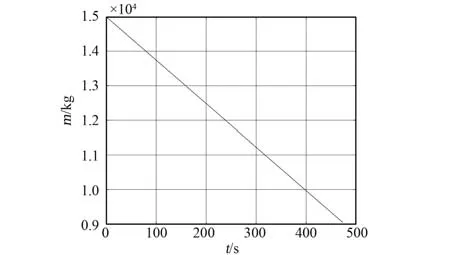
图8 燃料消耗曲线Fig.8 Fuel consumption

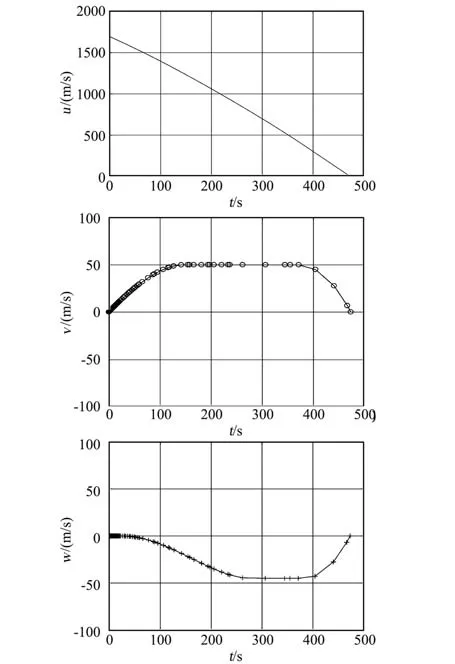
图9 组合体速度分量Fig.9 Velocity components of the spacecraft complex

从图中可以看出，全程处于开机状态，剩余质量在不断减少，同时3个速度分量最终达到终端速度要求。切向速度不断减小，而横向和径向由于存在应急条件约束，在中间时段速度大小保持在边界值附近，持续时间约为200 s。全过程的哈密尔顿函数结果如图10所示。整个软着陆过程的轨迹如图11所示。

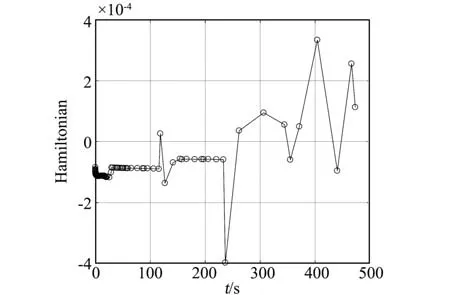
图10 哈密尔顿函数结果Fig.10 Results of Hamiltonian function

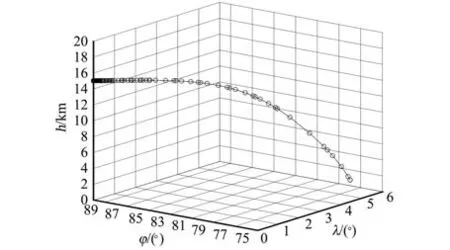
图11 组合体软着陆飞行轨迹Fig.11 Lunar soft-landing trajectory

由图10可知，全过程的哈密尔顿函数值约为0，满足一阶最优的必要条件，伪谱法能保证计算结果的最优性。从轨迹结果可知，整个软着陆过程轨迹平滑，无过大的机动，具备实际工程价值。

6 结论

1)基于SIM平台搭建的载人登月软着陆任务仿真系统采用月面着陆坐标系下的速度分量建立任务仿真单元，同时采用变网格Radau伪谱法作为任务规划单元，能够很好地实现软着陆任务过程的仿真。

2)变网格Radau伪谱法与其他方法的计算结果对比可知，算法可以在满足计算精度的同时，提高计算效率并获得了更优的计算结果。

3)由仿真结果可知，软着陆过程中总速度不断减少，且推力矢量始终位于水平面上方。在软着陆过程中横向和法向的速度幅值会先达到最大限制并以该极限值飞行一段时间后再逐渐降为0。