微重力下复合相变材料的热控性能数值仿真

李 达，杨春信，杨 涵，廖俊元

(北京航空航天大学航空科学与工程学院，北京100191)

1 引言

航天器电子设备的工作温度需要控制在正常范围内，温度过高会降低电子设备可靠性，导致飞行故障。相变材料是被动热控的主要方法之一，工作原理较为简单，就是利用材料相变过程中吸收和释放高潜热且温度几乎不变的特性，起到热控作用。这种特性对周期性工作的电子设备有很高的适用性。在电子设备开机或大功率工作期间，相变材料吸收热量并熔化；在关机或者低功率期间，相变材料将热量释放给热沉，可以有效地降低电子设备的温度波动。相变材料热控系统在航天领域已经有大量使用，例如阿波罗-15任务中的月球车利用相变材料吸收蓄电池产生的热量；漫游者火星着陆器采用相变材料对电池控温；NASA将微胶囊相变材料置于纺织物中，制成的航天服具有良好的温度调节功能[1]。中国嫦娥一号使用热管对光学元件热控，防止其温度过高[2]。

目前常用于航天器热控系统的相变材料是以石蜡为主的有机物。石蜡具有相变潜热高、性质稳定、无毒无污染、价格低等优点，且根据碳原子数的不同有着不同的相变范围，可以覆盖不同电子设备的工作温度，是一种优质的热控相变材料。但是，石蜡等有机相变材料的典型缺点是导热系数低，目前增强相变材料导热效率的方法主要有：①在相变材料中引入如纤维基体、泡沫金属材料等固定结构[3-4]；②加入细小的高导热材料颗粒如氧化铝、石墨烯粉末或金属粉末等[5-6]。第1种方法加工复杂，对相变材料容器内的空间要求较苛刻；相比之下第2种方法则更容易实现。其中，纳米氧化铝颗粒由于价格低廉、原料来源广、工艺简单等优点，作为一种优质导热填料广泛应用于复合相变材料的制备。

在航天器上，相变热控材料的研究需要考虑微重力的影响，尽管微重力的扰动幅度很小，但是会对相变材料熔化过程中的自然对流产生不同于地面环境下的影响，进而引起相变材料内部温度梯度的变化、固液界面的变化以及对电子设备热控效果的影响。尽管目前已有较多关于复合相变材料物性的研究与基于相变材料的热控系统性能研究，但考虑不同重力环境的相变储能结构仿真工作较少。

本文选择石蜡为相变材料，掺混Al2O3为导热增强剂，首次通过数值仿真的方法研究对比在微重力和重力条件下，掺入不同体积分数的复合相变材料相变过程和热控效果，以此判断是否达到温控的目标。

2 数值方法

2.1 数学模型

相变热控模型的计算域为25 mm×25 mm的二维矩形，内部为复合相变材料，左侧壁面为等热流密度边界，其他三侧为绝热边界。选择焓-多孔模型作为求解计算模型。该模型将焓作为系统因变量，在整个计算区域内建立统一的能量守恒方程，将固液混合的糊状区视为多孔介质，其中的液体体积分数类比为孔度，固态时液体体积分数为0，液态时为 1。 Paul[7]、Arasu[8]、Fen[9]等对相变材料数值研究中均采用了焓-多孔模型，实验与数值模拟结果的一致性良好。

求解相变材料的熔化以及凝固过程做如下假设：

1)液态石蜡被视为不可压缩牛顿流体，其密度根据Boussinesq近似设置；

2)石蜡被视为是各向同性材料，其热膨胀系数被忽略；

3)整个计算域初始温度均匀。

基于这些假设，相变过程中的控制方程为式(1)～(3)。

连续性方程：

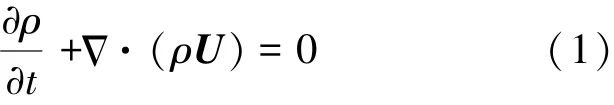
动量方程：

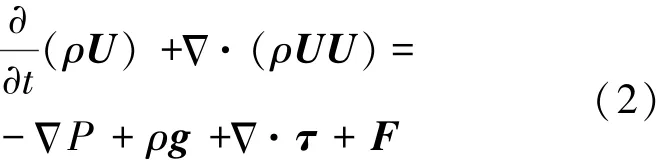
式中，P为静压，τ为应力张量，ρg和F分别是引力体积力和膨胀体积力。

能量方程：

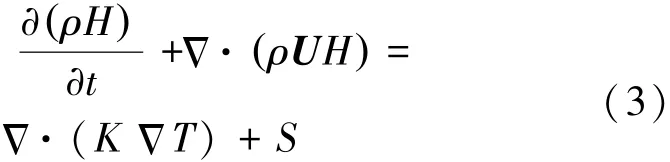
式中，H是相变材料的焓值，K是相变材料的导热系数，S是体积热源，在本文研究中，体积热源为0。

能量方程中的焓为相变材料的焓值，为显热和潜热的和，关系如式(4)所示。

式中，h为显热，其值为式(5)。

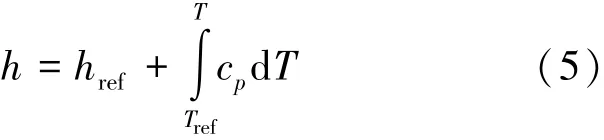
式中，href为参考焓值，Tref为参考温度，取值为273 K。

焓-多孔模型中的多孔度等效为相变材料液体体积分数，其定义为式(6)。

基于式(6)，潜热焓可以记为式(7)。

式中，L为潜热。

2.2 物性参数

在求解复合相变材料相变过程时，经过调研后采用式(8)～(16)的当量热物性以求解混合物的热物性。石蜡与Al2O3的物性如表1所示。

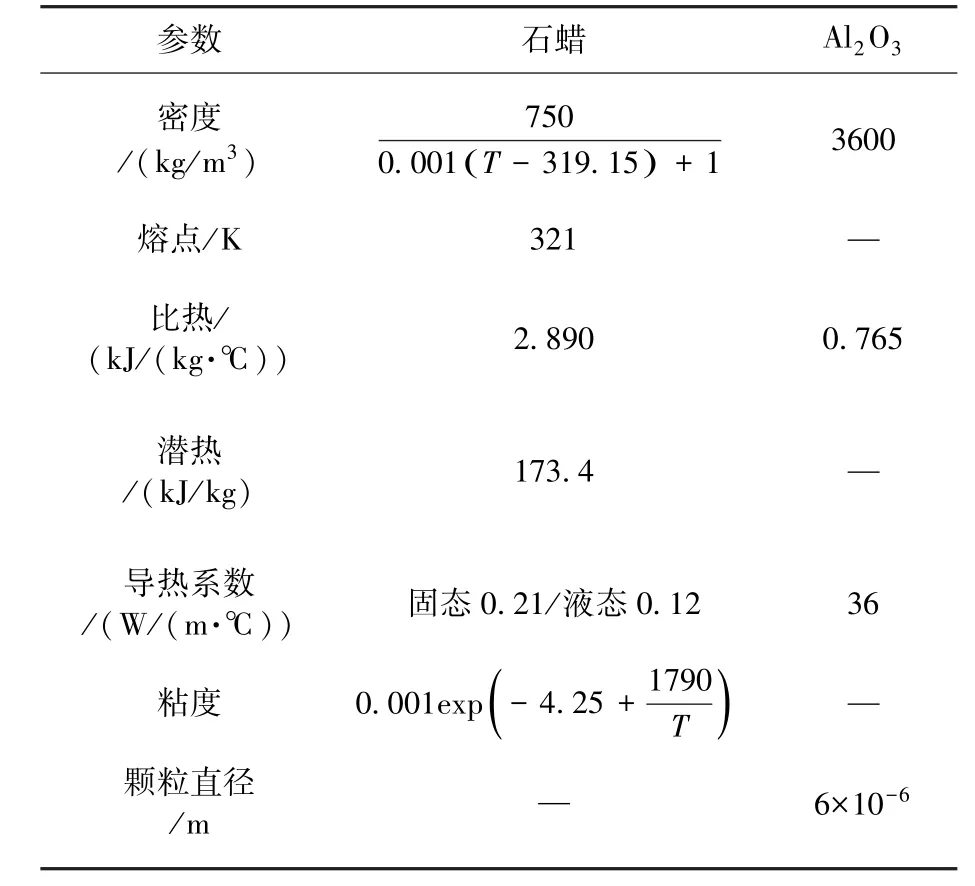
表1 石蜡与Al2O3的物性参数Table 1 Physical properties of paraffin and aluminum oxide

复合相变材料的当量物性与混合物的体积分数有关。制备时采用质量分数计量，体积分数与质量分数的换算关系如式(8)所示。

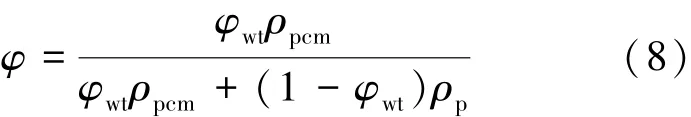
复合相变材料的密度关系如式(9)所示。

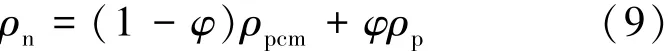
复合相变材料的定压比热容关系为式(10)。

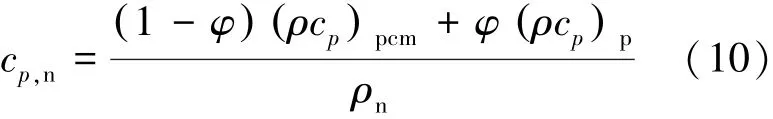
复合相变材料的潜热为式(11)。

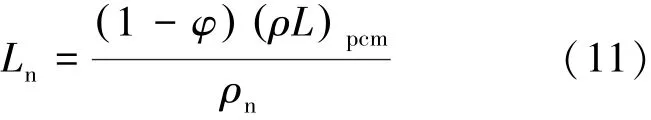
式中，下标pcm代表石蜡，p代表Al2O3，n代表掺混后的复合相变材料。

粘度根据Brinkman提出的含有小刚性球形颗粒的稀悬浮液的粘度计算方法，如式(12)所示。

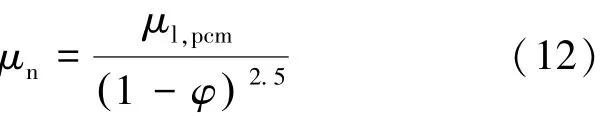
式中，下标l，pcm代表液态石蜡。

复合相变材料的有效导热系数计算方法为式(13)[10]。

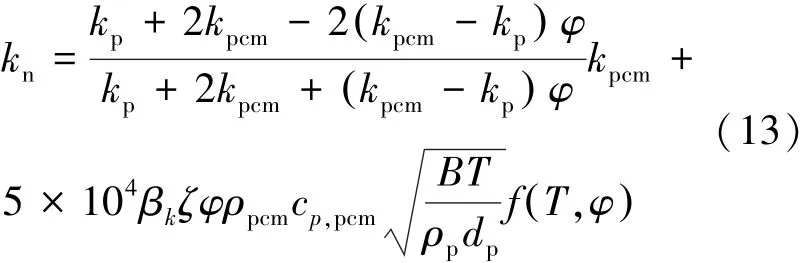
式中，B是Boltzmann常数，如式(14)所示：

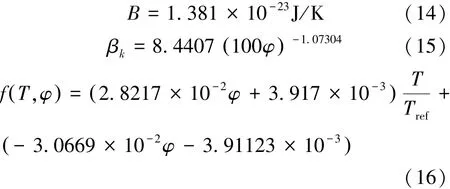
式中，Tref为参考温度，取273 K，式(14)的第1部分为Maxwell模型，第2部分是考虑布朗运动、温度的变化对导热系数的影响。参数ζ与布朗运动有关，由于在固体区域不存在布朗运动，取0，在液体区域与β取值相同。

使用ANSYS ICEM CFD划分全局结构网格，利用Fluent中基于焓-多孔模型的 solidification/melting模块计算，时间步长取0.1 s。

2.3 模型验证

Arasu[8]计算研究了石蜡与Al2O3混合相变材料在矩形容器内的熔化过程，其边界条件为上下等温边界、左右绝热边界，图1显示了本文计算模型与Arasu的对比。

如图1所示，尽管模拟的固液界面实验测量的结果稍有差异，但模拟结果误差较小，基本与实验结果一致，可以认为验证了仿真模型的正确性。分析这一差异的原因如下：

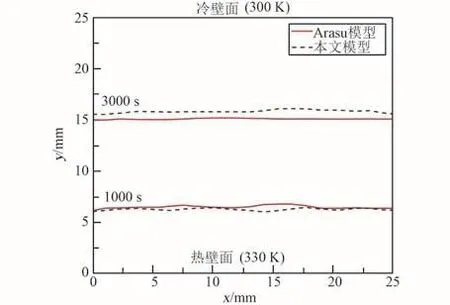
图1 模型验证Fig.1 Model verification

1)相变材料的物性随着温度的变化在Fluent中利用多项式拟合无法做到绝对精确。根据文献调研，石蜡的导热系数会随着温度的升高而降低，密度和粘度也会随着变化，所以会引起传热效率的变化，在仿真中这一部分的变化并不能精确体现，所以会导致计算结果稍有差异。

2)忽略了接触热阻。实际物理模型中，加热板与换热器底面因为粗糙度等原因，存在一定的接触热阻，这部分热阻主要是间隙中的空气热阻，在计算中忽略了接触热阻，会导致计算的传热系数大于实际值，从而导致整体传热效率的差异。

3 结果与分析

对复合相变材料(Al2O3质量分数为2%、3.5%和5%)分别进行微重力和重力条件下的数值仿真，得到相变材料熔化过程的温度变化、固液界面及加热面温度、熔化体积分数随时间的变化。

3.1 熔化过程

图2(a)和图2(b)分别展示了有重力、微重力条件下掺混比为5%的复合相变材料侧面1000 W/m2加热在 500 s、1500 s、3000 s3 个时刻的温度分布。在500 s时刻，温度刚达到相变材料熔点，此时相变材料的热量传递方式为导热，整个区域内几乎不存在自然对流，温度场是线性分布的，重力条件与微重力条件下的温度分布基本相同。在1500 s时，靠近加热面区域的相变材料已经完全熔化，重力条件下加热面温度为334 K，微重力下为346 K。此时，在重力条件下，液相区产生了剧烈的自然对流，温度分布不再是规则的线性分布，而是与自然对流的流动方向一致。在3000 s时，重力条件下液相区占比增大，重力驱动的自然对流对温度场的影响更加明显，在远离加热面的区域温度梯度已经近似平行于重力方向，等温线垂直于重力方向；而在微重力条件下，自然对流的影响极弱，热量传递以导热为主，温度梯度方向始终是垂直于加热面。

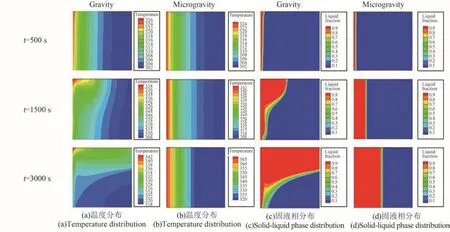
图2 5%掺混比的复合相变材料在重力和微重力条件下的熔化分布Fig.2 Melting distribution of composite phase change material with 5%blending ratio under gravity and microgravity conditions

图2(c)和图2(d)分别展示了有重力、微重力条件下掺混比为5%的复合相变材料侧面1000 W/m2加热在 500 s、1500 s、3000 s3 个时刻的固液界面的位置。在重力条件下，固液界面受自然对流的影响明显，在液相区形成了一个较大的旋转涡流，这导致了热流体随涡流运动到加热面附近的上半区域从而更早熔化，且随着时间推移，熔化区域越来越大，固液界面逐渐趋向与重力方向垂直。而在微重力条件下，固液界面完全平行于温度梯度方向和加热面。

3.2 熔化速率

图3为2%、3.5%和5%3种掺混比的复合相变材料在重力和微重力2种条件下的熔化体积分数随时间的变化，以此可以作为熔化速率的评判标准。重力条件下复合相变材料的熔化速率略高于微重力条件下，原因在于重力条件下存在自然对流以加速熔化。对比不同的掺混比，重力条件下3种掺混比熔化速率差别很小，高掺混比对应略大的熔化速率；而在微重力条件下，高掺混比所体现出来的熔化速率加快则更加明显，因为该条件下熔化速率主要取决于导热传热的强度，而掺入Al2O3提高了相变材料的导热系数。

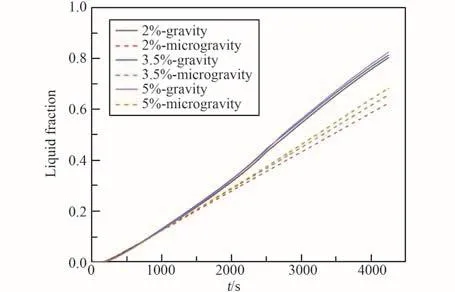
图3 熔化体积分数Fig.3 Melting volume fraction

3.3 热控性能

图4 为加热面在热流密度1000 W/m2下的温度变化，展示了质量分数为2%、3.5%和5%3种掺混比的复合相变材料在重力和微重力2种条件下对加热面温度的热控效果。在初始阶段，温度未达到相变材料融点，6条温度曲线基本重合。当开始相变时，在重力条件下，加热面温度保持稳定，不同掺混比的复合相变材料分别可以将加热面温度控制在50℃、55℃、58℃左右；在微重力条件下，加热面温度持续上升，上升速率相对于相变之前减小，但是加热面温度始终高于重力条件下的温度。造成这种差异的原因是相变材料熔化后液相区内的自然对流的强弱之别。重力是自然对流的驱动力之一。

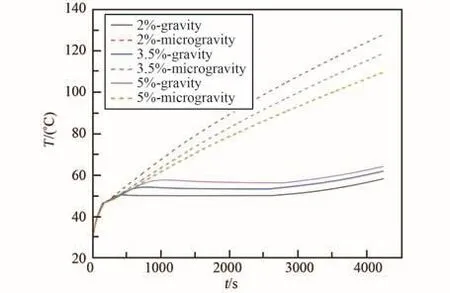
图4 加热面温度Fig.4 Temperature of the heating surface

在重力条件下，加热面热流可以被迅速传递到相变材料内部，壁面热量累积效应较小，温度较低；在微重力条件下，相变材料自身的导热系数较低，自然对流极弱，导致热量传递速率低，壁面的累积效应明显，温度持续升高。

在重力条件下，相变材料热控效果随着氧化铝掺混比的增加而恶化，加热面的稳定温度也更高。分析其原因，重力条件下相变材料的熔化特性是由导热与自然对流共同决定的，Al2O3颗粒的掺入在提高相变材料导热系数的同时也提高了相变材料的粘度，抑制了自然对流。因此，较低的Al2O3浓度表现出较好的热控性能，而且对于给定的外壳尺寸，由于相变材料含量更多，也能有更高的储能容量。

而在微重力条件下，高掺混比的复合相变材料的热控性能更佳，主要原因是在微重力下，自然对流缺少驱动力，热量传递基本完全依靠导热，所以导热性能的高低直接决定了其传热效率，掺混比更高的复合相变材料导热系数更大，因此热控性能更好。

4 结论

本文采用石蜡与Al2O3混合的复合相变材料，在等热流密度的边界条件下，定量地对比分析了复合相变材料在重力、微重力条件下的热控性能。通过数值仿真求解相变材料相变过程，主要得到以下结论：

1)相变材料的熔化特性取决于其导热性能和自然对流。在重力条件下，已熔化的液相区自然对流占据主导地位，而掺混Al2O3颗粒使复合相变材料粘度增加，从而抑制了自然对流，使热控性能变差；在微重力条件下，由于没有自然对流的驱动力，传热在液相区依然为导热主导，所以掺混Al2O3颗粒可以提高其导热性能，从而提高热控性能。由于没有自然对流的作用，微重力下的相变材料的熔化速率始终低于重力条件下。

2)当加热面为等热流密度边界时，重力条件下，相变材料可以达到将加热面温度控制在50～58℃左右的较好的热控效果，低掺混比的复合相变材料热控性能要优于高掺混比；在微重力条件下，复合相变材料的整体热控性能比重力条件下更差，无法达到持续温控的效果，此时高掺混比的复合相变材料热控性能要优于低掺混比。

因此，以航天任务作为热控应用背景时，应充分考虑自然对流和导热2个传热机制的不同作用，应当以微重力下最低导热增强剂掺混比的工况为最不利设计工况。本文结果可以为航天器相变热控设计提供理论基础。